Analysis 2.2 - Exponentialfunktion
1
Gegeben ist die in  definierte Funktion
definierte Funktion  mit
mit  Die Abbildung 1 zeigt den Graphen von
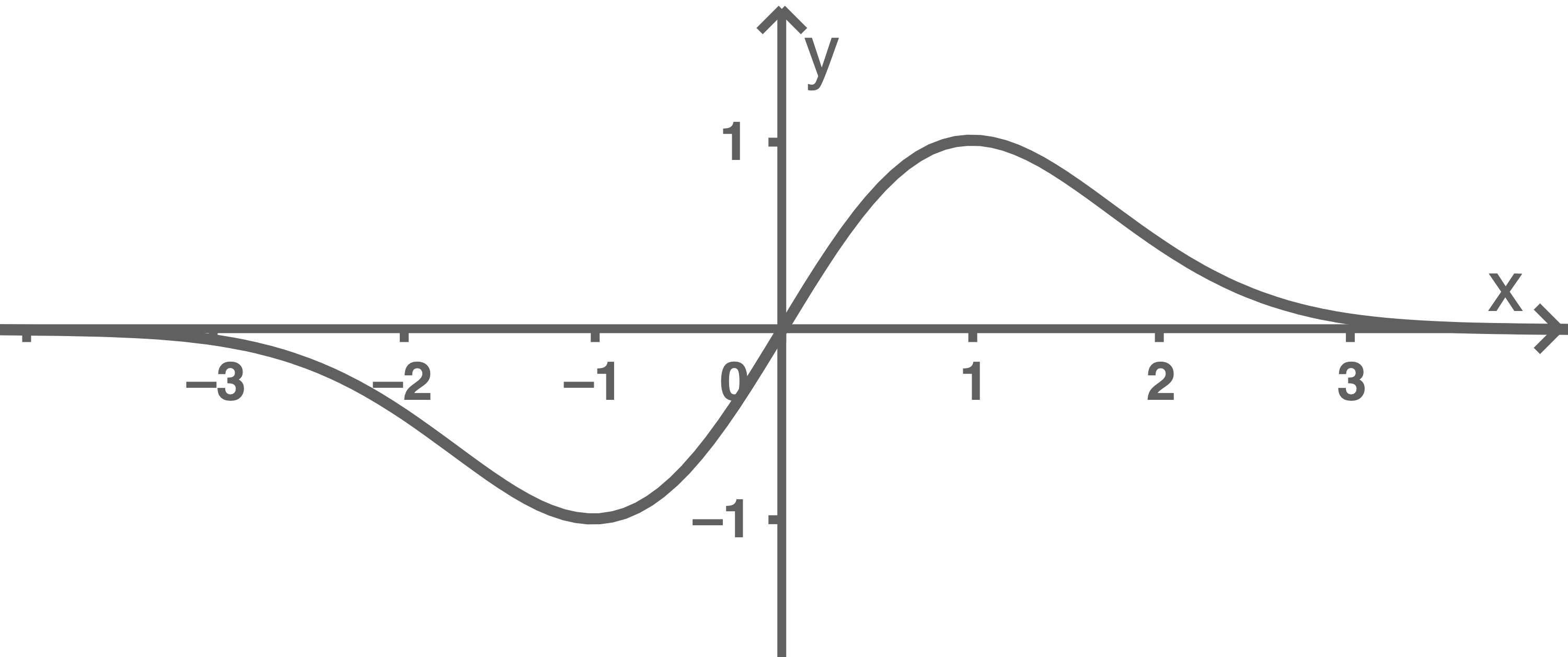
Die Abbildung 1 zeigt den Graphen von  ohne das zugrunde liegende Koordinatensystem.
ohne das zugrunde liegende Koordinatensystem.
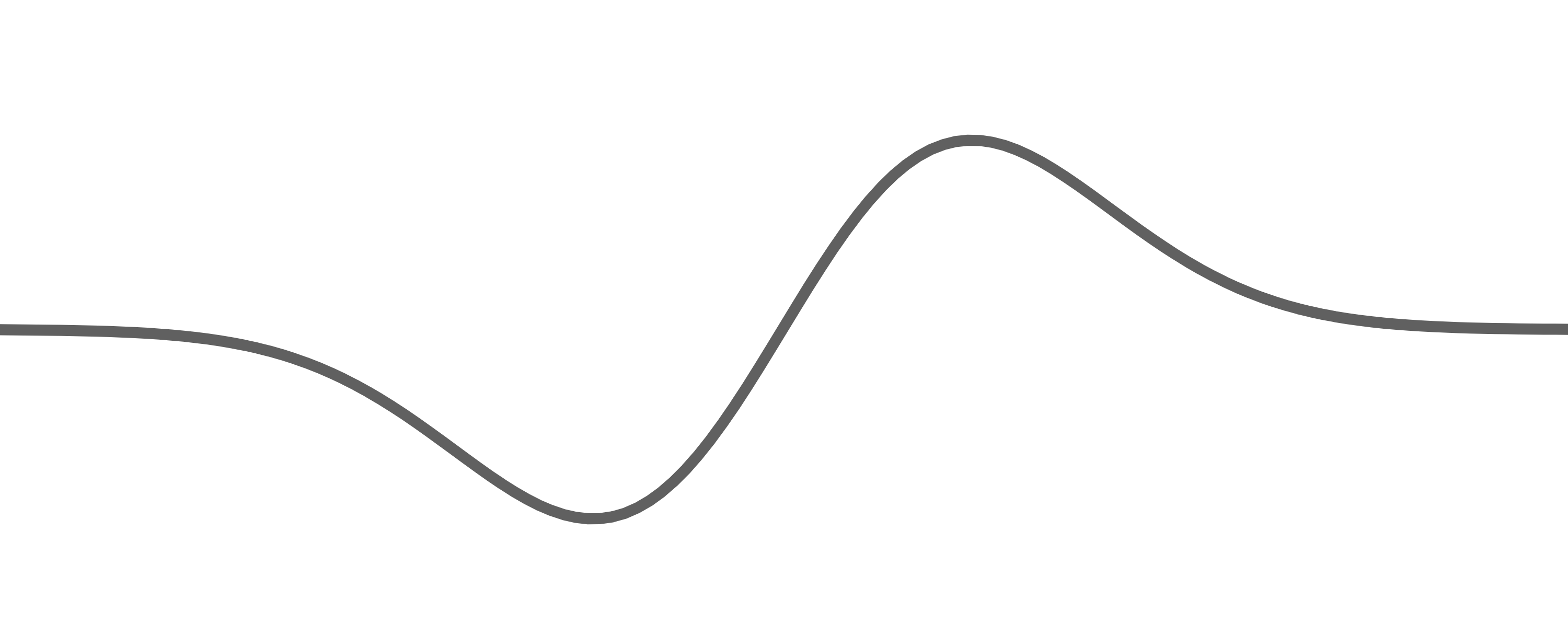

Abb. 1
a)
Zeige anhand des Funktionsterms von  , dass der Graph von
, dass der Graph von  symmetrisch bezüglich des Koordinatenursprungs ist.
symmetrisch bezüglich des Koordinatenursprungs ist.
Begründe, dass genau eine Nullstelle hat, und gib den Grenzwert von
genau eine Nullstelle hat, und gib den Grenzwert von  für
für  an.
an.
Begründe, dass
(4 BE)
b)
Bestimme einen Term der ersten Ableitungsfunktion  von
von  [Zur Kontrolle:
[Zur Kontrolle:  ]
]
(2 BE)
c)
Untersuche rechnerisch das Monotonieverhalten von 
Ergänze in der Abbildung 1 die Koordinatenachsen und skaliere diese passend.
Ergänze in der Abbildung 1 die Koordinatenachsen und skaliere diese passend.
(5 BE)
d)
Der Graph von  besitzt im I. Quadranten einen Wendepunkt.
besitzt im I. Quadranten einen Wendepunkt.
Zeige, dass die Koordinaten dieses Punktes sind.
sind.
Gib die Koordinaten des Wendepunktes des Graphen von im III. Quadranten an.
Hinweis: Ohne Nachweis kann verwendet werden
im III. Quadranten an.
Hinweis: Ohne Nachweis kann verwendet werden 
Zeige, dass die Koordinaten dieses Punktes
Gib die Koordinaten des Wendepunktes des Graphen von
(3 BE)
e)
Die folgende Rechnung stellt die Lösung einer Aufgabe dar.

 Formuliere eine passende Aufgabenstellung.
Formuliere eine passende Aufgabenstellung.
(3 BE)
f)
An den Graphen von  werden im I. Quadranten Tangenten gelegt, die jeweils die
werden im I. Quadranten Tangenten gelegt, die jeweils die  -Achse in einem Punkt
-Achse in einem Punkt  schneiden.
schneiden.
Beurteile folgende Aussage:
Es gibt eine Tangente mit
Beurteile folgende Aussage:
Es gibt eine Tangente mit
(4 BE)
g)
Ist  die erste Ableitungsfunktion einer in
die erste Ableitungsfunktion einer in  definierten Funktion
definierten Funktion  so gilt
so gilt

Berechne damit den Wert des Terms
Berechne damit den Wert des Terms
(3 BE)
h)
Interpretiere den folgenden Sachverhalt geometrisch:
Für jede Stammfunktion  von
von  und für jede reelle Zahl
und für jede reelle Zahl  gilt
gilt 
(3 BE)
2
Betrachtet wird nun die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit 
 und
und  einteilen:
einteilen:


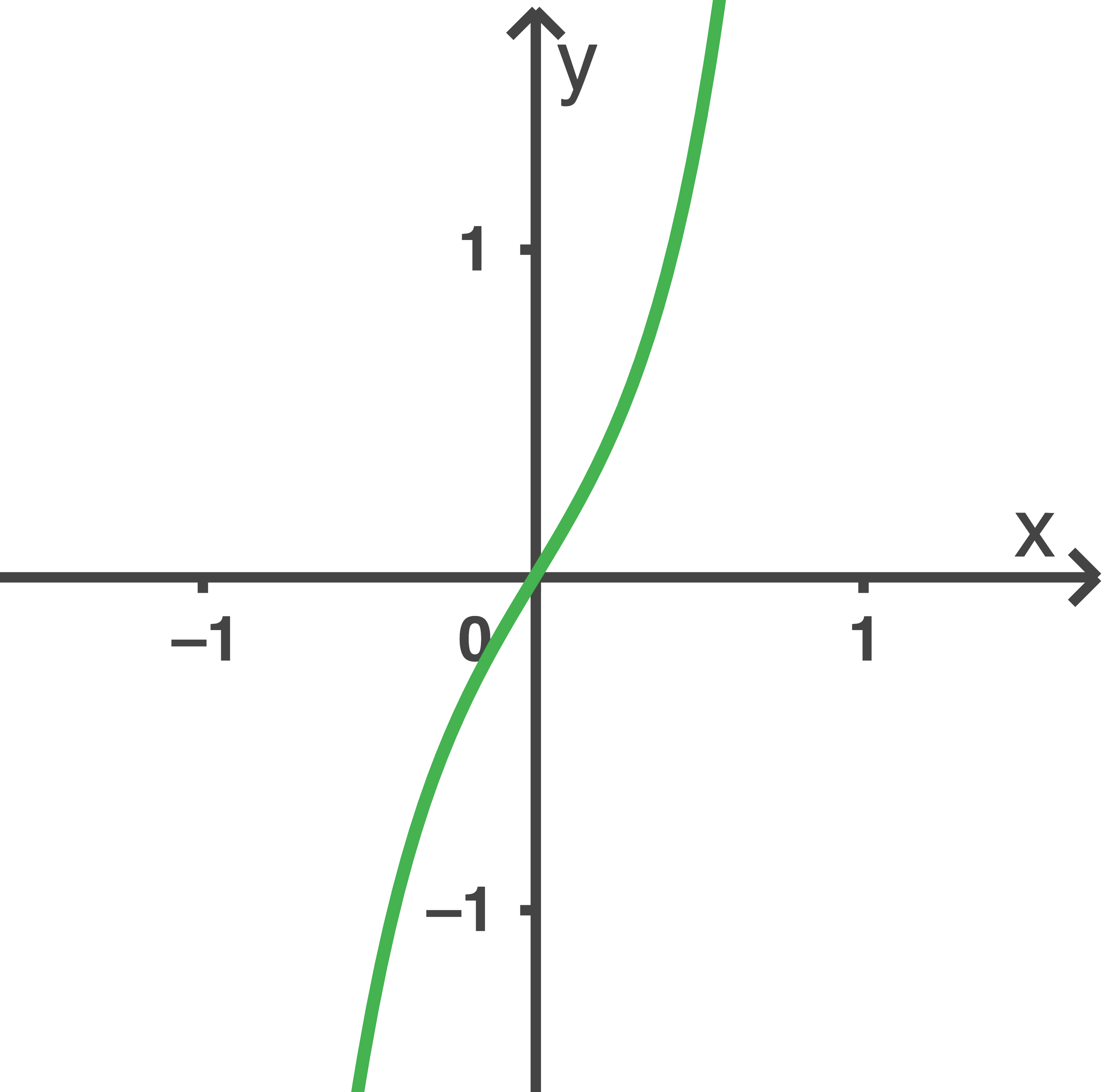
 die Abbildung 3 einen Graphen der Gruppe
die Abbildung 3 einen Graphen der Gruppe 
 Die Extremstellen von
Die Extremstellen von  stimmen mit den Lösungen der Gleichung
stimmen mit den Lösungen der Gleichung  überein.
überein.
a)
Zeige, dass genau ein Graph der Schar den Punkt  enthält, und gib den zugehörigen Wert von
enthält, und gib den zugehörigen Wert von  an.
an.
(3 BE)
b)
Der Graph der Funktion  ist eine Gerade. Gib die Steigung dieser Gerade und die Koordinaten ihres Schnittpunkts mit der
ist eine Gerade. Gib die Steigung dieser Gerade und die Koordinaten ihres Schnittpunkts mit der  -Achse an.
-Achse an.
(2 BE)
c)
Die folgenden Aussagen gelten für alle reellen Zahlen  und
und 
oder
(3 BE)
d)
Zeige, dass die folgende Aussage für jeden Wert von  richtig ist:
Wird der Graph von
richtig ist:
Wird der Graph von  mit dem gleichen Faktor
mit dem gleichen Faktor  sowohl in
sowohl in  -Richtung als auch in
-Richtung als auch in  -Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.
-Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.
Die Graphen der Schar lassen sich in die folgenden Gruppen
(3 BE)
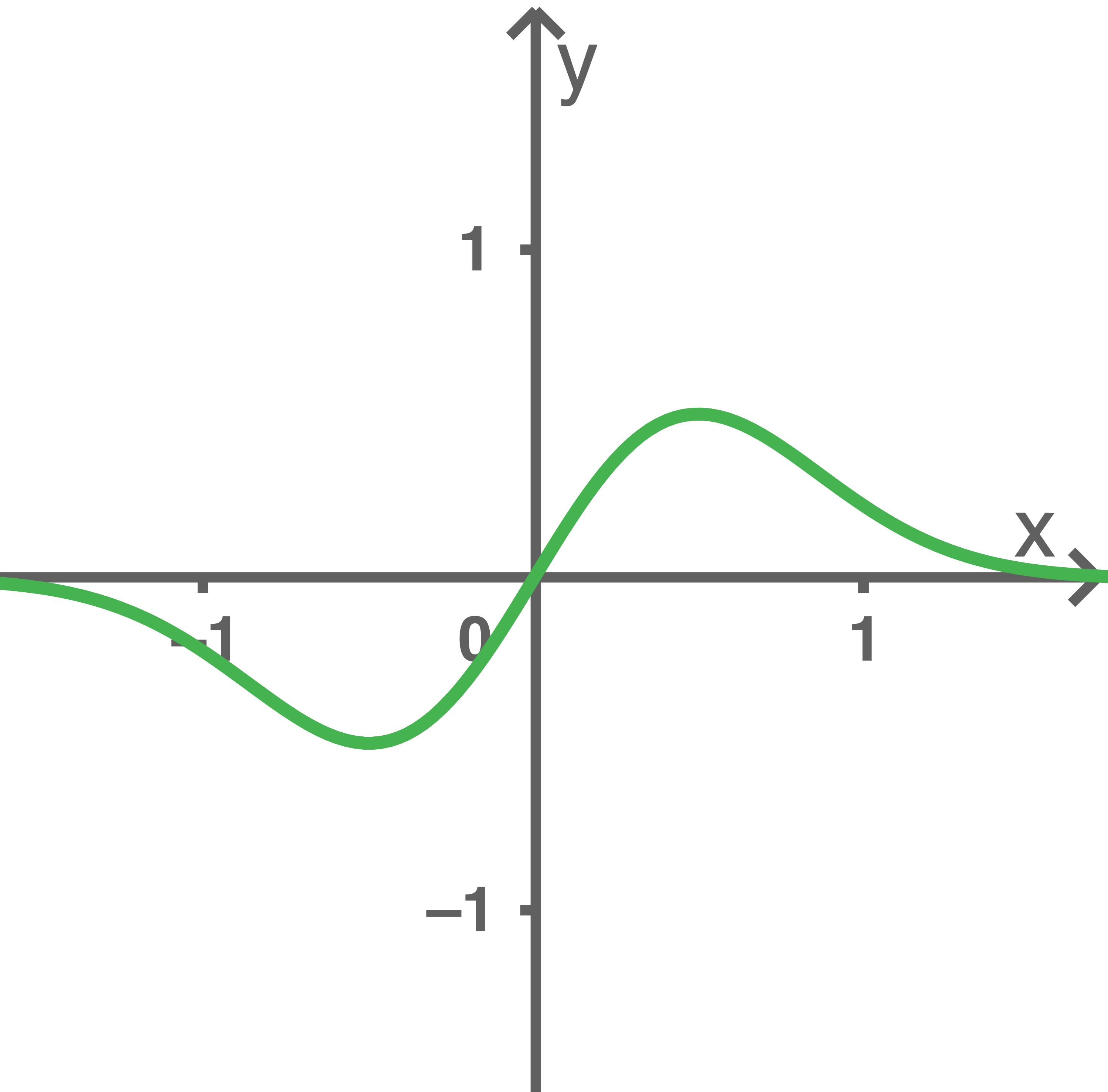
Der Graph hat genau zwei Extrempunkte.
Der Graph hat keine Extrempunkte.
Die Abbildung 2 zeigt einen Graphen der Gruppe 
Abb. 2

Abb. 3
e)
Gib zu jeder der beiden Gruppen  und
und  alle zugehörigen Werte von
alle zugehörigen Werte von  an und begründe deine Angabe.
an und begründe deine Angabe.
(3 BE)
f)
Alle Extrempunkte der Graphen der Schar liegen auf einer Gerade.
Begründe, dass es sich dabei um die Gerade mit der Gleichung handelt.
handelt.
Begründe, dass es sich dabei um die Gerade mit der Gleichung
(3 BE)
g)
Für jeden positiven Wert von  bilden der Hochpunkt
bilden der Hochpunkt  des Graphen von
des Graphen von  der Punkt
der Punkt  der Koordinatenursprung und der Punkt
der Koordinatenursprung und der Punkt  die Eckpunkte eines Vierecks. Bestimme ausgehend von einer geeigneten Skizze denjenigen Wert von
die Eckpunkte eines Vierecks. Bestimme ausgehend von einer geeigneten Skizze denjenigen Wert von  für den das Viereck den Flächeninhalt
für den das Viereck den Flächeninhalt  hat.
hat.
(6 BE)
(50 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
Mit der Produktregel folgt:

c)
Monotonieverhalten
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/d9fbb26298d66777f1e70cc293264c3bb3279a59ee92b07653320157bd090993?color=5a5a5a) Mit dem Satz vom Nullprodukt folgen die Extremstellen:
Mit dem Satz vom Nullprodukt folgen die Extremstellen:  und
und  Die Funktion
Die Funktion  ist für
ist für  wegen
wegen  streng monoton zunehmend, für
streng monoton zunehmend, für  und
und  wegen
wegen  streng monoton abnehmend.
Es gilt
streng monoton abnehmend.
Es gilt  Achsenskalierung
Durch die Extremstellen können nun die Achsen skaliert werden.
Achsenskalierung
Durch die Extremstellen können nun die Achsen skaliert werden.

d)
Es gilt:  Damit ist die notwendige Bedingung für Wendestellen erfüllt. Auf den Nachweis der hinreichenden Bedingung für Wendestellen kann verzichtet werden, da die Existenz einer Wendestelle gegeben ist.
Damit ist die notwendige Bedingung für Wendestellen erfüllt. Auf den Nachweis der hinreichenden Bedingung für Wendestellen kann verzichtet werden, da die Existenz einer Wendestelle gegeben ist.
 Somit folgen die Koordinaten des Wendepunktes im I. Quadranten mit:
Somit folgen die Koordinaten des Wendepunktes im I. Quadranten mit:  Die Koordinaten des Wendepunktes im III. Quadranten folgen wegen der Symmetrie des Graphen mit:
Die Koordinaten des Wendepunktes im III. Quadranten folgen wegen der Symmetrie des Graphen mit: 
e)
Mögliche Aufgabenstellung:
Ermittle die  -Werte der Punkte des Graphen von
-Werte der Punkte des Graphen von  an denen die Steigung der Tangente genauso groß ist wie die Steigung der Sekante durch die beiden Wendepunkte.
an denen die Steigung der Tangente genauso groß ist wie die Steigung der Sekante durch die beiden Wendepunkte.
f)
Tangentengleichung an den Graphen von  im Wendepunkt aufstellen
im Wendepunkt aufstellen
 Die Steigung ergibt sich mit
Die Steigung ergibt sich mit  Durch Einsetzen von
Durch Einsetzen von  und der Koordinaten des Wendepunktes in
und der Koordinaten des Wendepunktes in  folgt:
folgt:
![\(\begin{array}[t]{rll}
\dfrac{\sqrt{3}}{\mathrm e}&=& -\dfrac{2}{\mathrm e} \cdot \sqrt{3} +n &\quad \scriptsize \mid\;+\dfrac{2 \sqrt{3}}{\mathrm e} \\[5pt]
\dfrac{3\sqrt{3}}{\mathrm e}&=& n
\end{array}\)](https://mathjax.schullv.de/46c1f8d028276ec86fc2defc222f8ccbc581054faae707873a6dc564f0b1db66?color=5a5a5a) Die Tangentengleichung folgt mit
Die Tangentengleichung folgt mit  und schneidet die
und schneidet die  -Achse im Punkt
-Achse im Punkt  Somit gilt
Somit gilt  Die Aussage ist folglich richtig.
Die Aussage ist folglich richtig.
g)
Es gilt:
![\(\begin{array}[t]{rll}
f(x)&=& x \cdot \mathrm e^{-\frac{1}{2} \cdot x^2+\frac{1}{2}} \\[5pt]
&=& g](https://mathjax.schullv.de/4b8a49e4d639aa499075269d5b3eb9389de603de037d124e5455503202be4338?color=5a5a5a) Es gilt somit:
Es gilt somit:
![\(\begin{array}[t]{rll}
g(x) &=& -\dfrac{1}{2} \cdot x^2+\dfrac{1}{2} \\[5pt]
g](https://mathjax.schullv.de/5ad308be5b014c364333c31de1cbe59b405120d7a9c76a5b8ce9b309b1e68d65?color=5a5a5a) Daraus folgt:
Daraus folgt:

![\(=-\displaystyle\int_0^1(-x) \cdot \mathrm e^{-\frac{1}{2} x^2+\frac{1}{2}} \mathrm d x=-\left[\mathrm e^{-\frac{1}{2} x^2+\frac{1}{2}}\right]_0^1
\)](https://mathjax.schullv.de/54c244ab610dd4a4461e5b917b954e05f8f8bc21596e499cc14a42f04cb64b4f?color=5a5a5a)


h)
Für jede reelle Zahl  schließen der Graph von
schließen der Graph von  die
die  -Achse und die Gerade mit der Gleichung
-Achse und die Gerade mit der Gleichung  ein Flächenstück ein. Dessen Inhalt stimmt ungefähr mit dem Inhalt des Flächenstücks überein, das der Graph von
ein Flächenstück ein. Dessen Inhalt stimmt ungefähr mit dem Inhalt des Flächenstücks überein, das der Graph von  die
die  -Achse und die Gerade mit der Gleichung
-Achse und die Gerade mit der Gleichung  einschließen.
einschließen.
2
a)
Einsetzen in die Funktionsgleichung:
![\(\begin{array}[t]{rll}
f_a(1) &=& 1 \\[5pt]
1 \cdot \mathrm e^{-\frac{1}{2} a \cdot 1^{2}+\frac{1}{2}} &=& 1 \\[5pt]
\mathrm e^{-\frac{1}{2} a +\frac{1}{2}}&=& 1 &\quad \scriptsize \mid\; \ln\\[5pt]
-\frac{1}{2} a +\frac{1}{2} &=& 0 &\quad \scriptsize \mid\;-\frac{1}{2} \\[5pt]
-\frac{1}{2} a &=& -\frac{1}{2} &\quad \scriptsize \mid\;\cdot (-2) \\[5pt]
a &=& 1
\end{array}\)](https://mathjax.schullv.de/f6ee63dc7ea55ccc412329dad1306c341f79024cfda70fdefadd5f4dcdff9b9a?color=5a5a5a) Die Gleichung
Die Gleichung  hat genau eine Lösung. Daher enthält genau ein Graph der Schar den Punkt
hat genau eine Lösung. Daher enthält genau ein Graph der Schar den Punkt  Dies ist der Graph zu
Dies ist der Graph zu  mit
mit 
b)
c)
Alle Graphen der Schar schneiden sich im Koordinatenursprung und haben dort die gleiche Steigung. Keiner der Graphen hat einen weiteren Punkt mit einem anderen Graphen der Schar gemeinsam.
d)
Es gilt:
![\(\begin{array}[t]{rll}
k \cdot f_a \left(\dfrac{x}{k}\right) &=& k\cdot \dfrac{x}{k} \cdot \mathrm e^{-\frac{1}{2}\cdot (\frac{x}{k})^2 +\frac{1}{2}} \\[5pt]
&=& x\cdot \mathrm e^{-\frac{1}{2}\cdot \frac{1}{k^2}\cdot x^2 +\frac{1}{2}} \\[5pt]
&=&f_{\frac{a}{k^2}}(x)
\end{array}\)](https://mathjax.schullv.de/71484036d6c3ffcd47eb26b0bc1942e348eeba2871c3d6edbab3a9d9c5635a48?color=5a5a5a)
e)
Die Extremstellen von  sind laut Aufgabenstellung die Lösungen der Gleichung
sind laut Aufgabenstellung die Lösungen der Gleichung  Um die Gleichung zu lösen, müsste durch
Um die Gleichung zu lösen, müsste durch  geteilt werden. Für
geteilt werden. Für  ist dies nicht möglich, wodurch die Gleichung dann keine Lösung hat.
ist dies nicht möglich, wodurch die Gleichung dann keine Lösung hat.
Für besitzt die Gleichung ebenfalls keine Lösung, da
besitzt die Gleichung ebenfalls keine Lösung, da  dann negativ sein müsste, was nicht möglich ist.
dann negativ sein müsste, was nicht möglich ist.
Für alle positiven Werte von hat die Gleichung genau zwei Lösungen. Insgesamt ergibt sich daraus:
Zu den Graphen
hat die Gleichung genau zwei Lösungen. Insgesamt ergibt sich daraus:
Zu den Graphen  gehören alle Graphen von
gehören alle Graphen von  mit
mit  Zu den Graphen
Zu den Graphen  gehören alle Graphen von
gehören alle Graphen von  mit
mit 
Für
Für alle positiven Werte von
f)
Für die Extremstellen von  gilt
gilt  Daraus folgt bereits
Daraus folgt bereits  Die Gleichung kann daher wie folgt nach
Die Gleichung kann daher wie folgt nach  umgeformt werden:
umgeformt werden:
 Einsetzen in die Funktionsgleichung von
Einsetzen in die Funktionsgleichung von  liefert:
liefert:

 Daher liegen alle Extrempunkte der Graphen von
Daher liegen alle Extrempunkte der Graphen von  auf der Geraden mit der Gleichung
auf der Geraden mit der Gleichung 
g)