Analysis 2.2
Bremsschuh
Gegeben ist die Funktionsschar
a)
Ermittle die Koordinaten der Schnittpunkte von  mit den beiden Koordinatenachsen in Abhängigkeit von
mit den beiden Koordinatenachsen in Abhängigkeit von  .
.
Gib das Verhalten der Funktionswerte von für
für  und
und  an.
an.
Gib das Verhalten der Funktionswerte von
(6P)
b)
Jeder Graph  hat im Punkt
hat im Punkt  eine zur
eine zur  -Achse parallele Tangente. Zur Ermittlung des
-Achse parallele Tangente. Zur Ermittlung des  -Wertes dieses Punktes hat ein Schüler den folgenden Lösungsweg korrekt angegeben:
1.
-Wertes dieses Punktes hat ein Schüler den folgenden Lösungsweg korrekt angegeben:
1.  2.
2.  3.
3.  4.
4.  Gib drei Regeln an, die beim Ableiten des Funktionsterms von
Gib drei Regeln an, die beim Ableiten des Funktionsterms von  genutzt worden sind und begründe die Umformung von Gleichung 2 und Gleichung 3.
genutzt worden sind und begründe die Umformung von Gleichung 2 und Gleichung 3.
Zeige, dass für der Punkt
der Punkt  ein lokaler Extrempunkt von
ein lokaler Extrempunkt von  ist.
ist.
Bestimme dessen Koordinaten sowie die Art des Extremums.
Zeige, dass für
Bestimme dessen Koordinaten sowie die Art des Extremums.
(11P)
c)
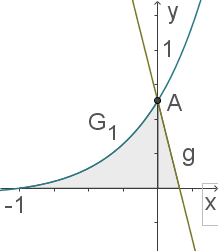
Der Graph  und die Gerade
und die Gerade  mit der Gleichung
mit der Gleichung  begrenzen gemeinsam mit der
begrenzen gemeinsam mit der  -Achse eine Fläche, die dem Querschnitt eines Bremsschuhs entspricht, der das Wegrollen von Fahrzeugen verhindert (1 LE=25
-Achse eine Fläche, die dem Querschnitt eines Bremsschuhs entspricht, der das Wegrollen von Fahrzeugen verhindert (1 LE=25 cm).
Die „Tiefe“ des Bremsschuhs beträgt 20
cm).
Die „Tiefe“ des Bremsschuhs beträgt 20 cm.
cm.
Zeige, dass sich und
und  auf der
auf der  -Achse schneiden.
-Achse schneiden.
Berechne das Volumen eines solchen Bremsschuhs.
Zeige, dass sich
Berechne das Volumen eines solchen Bremsschuhs.
(13P)
d)
Ermittle die Größe des Winkels, den  und
und  im Punkt
im Punkt  einschließen.
einschließen.
(5P)
e)
Der Produzent der Bremsschuhe möchte auf der Querschnittsfläche des Bremsschuhs sein rechteckiges Firmenlogo mit den Seitenlängen 5 cm und 15
cm und 15 cm so einstanzen lassen, dass die längere der beiden Seiten parallel zur
cm so einstanzen lassen, dass die längere der beiden Seiten parallel zur  -Achse verläuft.
-Achse verläuft.
Untersuche, ob das möglich ist.
Untersuche, ob das möglich ist.
(5P)
(40P)
Aufgabe 1.2: Bremsschuh
a)
b)
- Summenregel:
- Kettenregel:
- Ableitung eines Vielfachen:
Hinreichende Bedingung:
Hinreichende Bedingung Hochstelle:
c)
d)
e)