Hilfsmittelfreier Teil

1.1 Analysis

Die Abbildung zeigt den Graphen einer Funktion $f$ . Die Achseneinteilung der $y$ -Achse ist nicht bekannt.

Gegeben sind die folgenden drei Funktionsgleichungen:

(I) $f_1(x)=x^2\cdot\left(x^2-4\right)$

(II) $f_2(x)=x\cdot\left(x^2-2x\right)$

(III) $f_3(x)=x^3\cdot\left(x-2\right)$

Untersuche für jede der Funktionsgleichungen (I), (II) und (III), ob sie den abgebildeten Graphen $G_f$ beschreiben kann. Begründe jeweils deine Entscheidung.

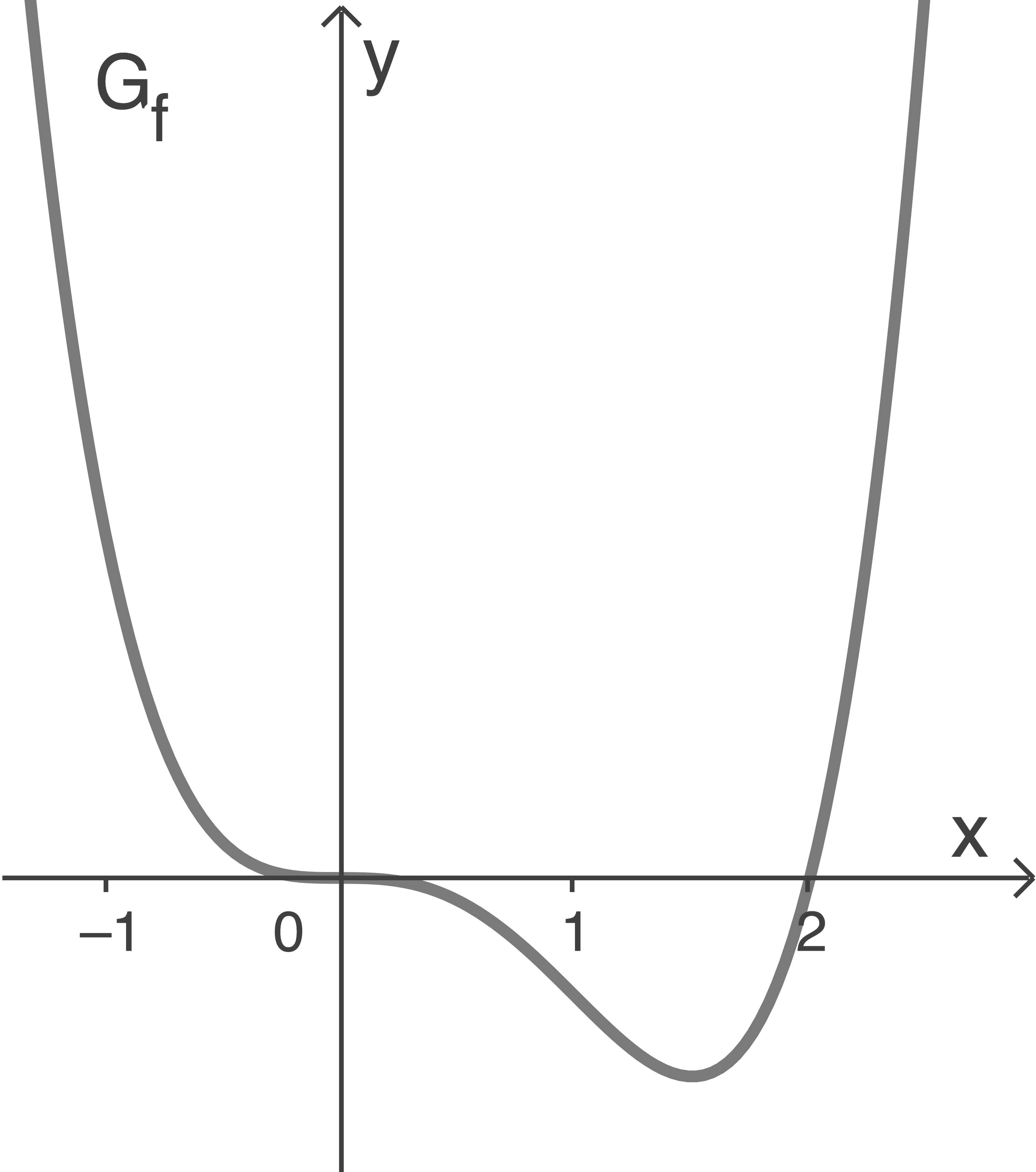
Grafik eines mathematischen Funktionsgraphen mit den Achsen x und y.

(5 BE)

1.2 Analysis

Gegeben ist eine in $\mathbb{R}$ definierte Funktion $f$ mit $f(x)=x^4-k\cdot x^2$ , wobei $k$ eine positive reelle Zahl ist. Die Abbildung zeigt den Graphen von $f.$

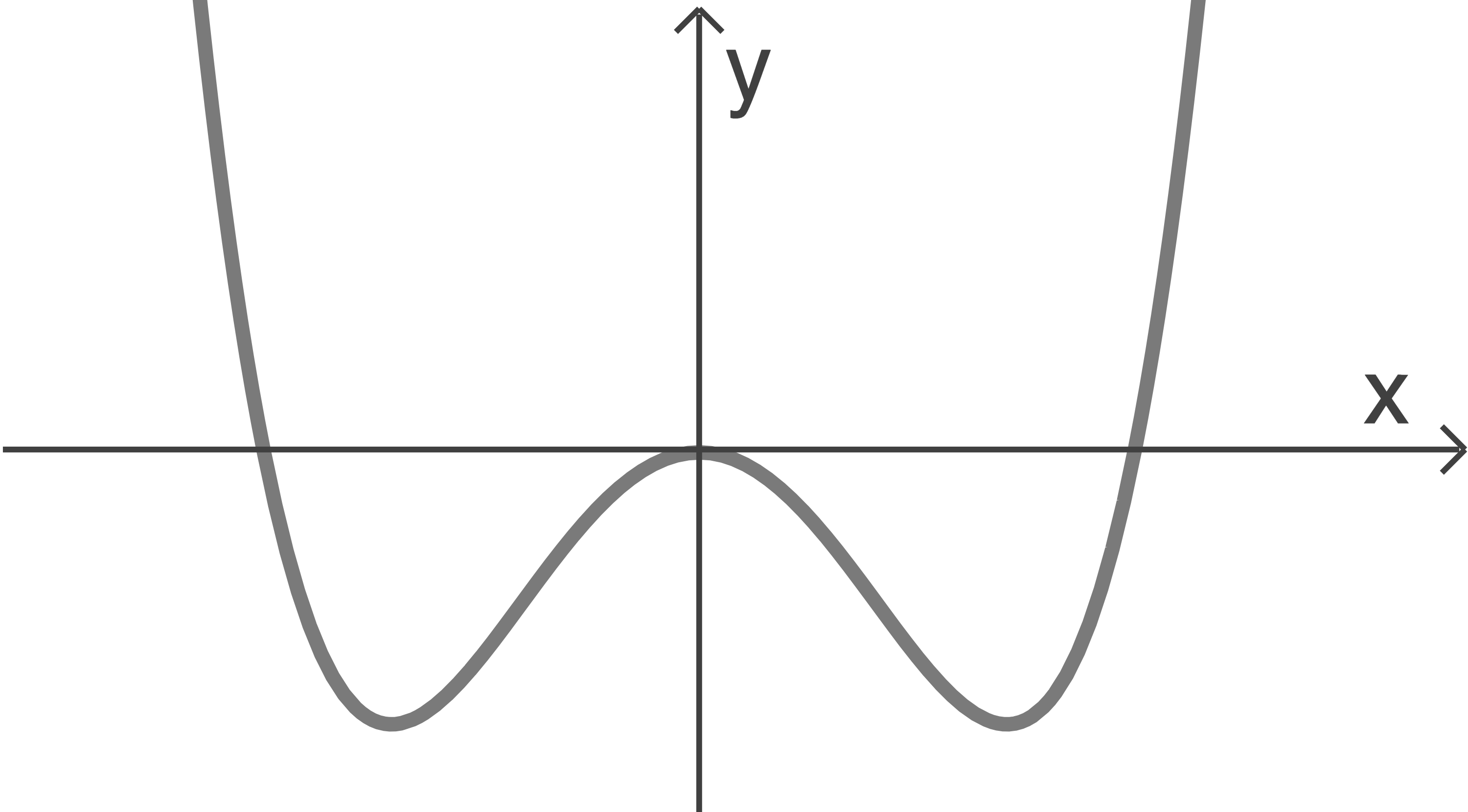
Graf einer mathematischen Funktion mit den Achsen x und y. Die Kurve zeigt eine symmetrische Form.

Zeige, dass $\(f$ eine Gleichung der ersten Ableitungsfunktion von $f$ ist.

(1 BE)

Die beiden Tiefpunkte des Graphen von $f$ haben jeweils die y-Koordinate $-1.$
Ermittle den Wert von $k.$

(4 BE)

1.3 Analysis

Die Abbildung zeigt den Graphen einer Stammfunktion $F$ von $f$ .

Grafik eines Funktionsgraphen mit x- und y-Achse, der eine Kurve darstellt.

Bestimme mithilfe der Abbildung näherungsweise den Funktionswert von $f$ an der Stelle $0.$

(1 BE)

Gib ein Intervall $[a;b]$ mit $a,b\,\in\mathbb{R}$ an, so dass gilt: $\displaystyle\int_{a}^{b}f(x)\;\mathrm dx=0$ .
Begründe deine Aussage.

(2 BE)

Untersuche, ob es eine Stelle $x_s\,\in[0;7]$ gibt, für die gilt:
$f$ ist an der Stelle $x_s$ monoton steigend.
Gib ggf. einen möglichen Wert für $x_s$ an.

(2 BE)

1.4 Analysis

Gegeben ist die Funktion $f$ durch $f(x)=\ln\left(2x-5\right)$ ; $x\,\in\mathbb{R}$ , $x\gt2,5$ .

Zeige, dass $x_0=3$ eine Nullstelle von $f$ ist.

(1 BE)

Die Normale $h$ an den Graphen der Funktion $f$ im Punkt $S\left(3\mid0\right)$ schließt mit den beiden Koordinatenachsen ein Dreieck ein.
Berechne den Flächeninhalt dieses Dreiecks.

(4 BE)

1.5 Geometrie

Betrachtet werden die Ebene $E:\,x_1-x_2+x_3-3=0$ und für $a\in\mathbb{R}$ die Geraden

$g_a:\, \vec{x}=\pmatrix{1\\-2\\0}+\lambda\cdot\pmatrix{2\\1+a\\2}$ mit $\lambda \in \mathbb{R}.$

Bestimme denjenigen Wert von $a$ , für den die Gerade $g_a$ senkrecht zu $E$ steht.

(2 BE)

Untersuche, ob es einen Wert von $a$ gibt, für den die Gerade $g_a$ in $E$ liegt.

(3 BE)

1.6 Geometrie

Gegeben ist die Ebenenschar $E_a:\,a\cdot x+\left(2+a\right)\cdot y-2\cdot z=6$ ; $a\in\mathbb{R}$ , $a\gt0.$

Untersuche, ob es einen Wert von $a$ gibt, für den die Schnittpunkte der Ebene $E_a$ mit den Koordinatenachsen ein gleichseitiges Dreieck bilden.

(5 BE)

(30 BE)

1.5 Stochastik

Die Vierfeldertafel gehört zu einem Zufallsexperiment mit Ereignissen $A$ und $B.$ Für die Wahrscheinlichkeit $p$ gilt $p\neq0.$

	$B$
$A$	$p$	$3p$
$\overline{A}$		$1-3p$
	$4p$

Vervollständige die Vierfeldertafel. Zeige, dass $p$ nicht den Wert $\frac{1}{5}$ haben kann.

(3 BE)

Für einen bestimmten Wert von $p$ sind $A$ und $B$ stochastisch unabhängig. Ermittle diesen Wert von $p.$

(2 BE)

1.6 Stochastik

In einer Urne befinden sich zwei rote und acht schwarze, sonst nicht unterscheidbare Kugeln.
Zwei Kugeln werden nacheinander ohne Zurücklegen gezogen.
Bestimme die Wahrscheinlichkeit dafür, dass dabei genau eine rote Kugel gezogen wird.

(2 BE)

In einer Urne befinden sich eine rote und $n$ schwarze Kugeln.
Zwei Kugeln werden nacheinander ohne Zurücklegen gezogen.
Bestimme den kleinsten Wert für $n,$ für den gilt:
Die Wahrscheinlichkeit dafür, dabei keine rote Kugel zu ziehen, beträgt mindestens 90 %.

(3 BE)

(30 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1 Analysis

An der Abbildung des Graphen können die Nullstellen bei $x=0$ und $x=2$ abgelesen werden.
Für $x\rightarrow\pm\infty$ gilt zudem $f(x)\to \infty.$

Die Funktion $f_1$ beschreibt den Graphen nicht, da sie eine zusätzliche Nullstelle bei $x=-2$ besitzt.

Die Funktion $f_2$ beschreibt den Graphen ebenfalls nicht, da für $x\rightarrow-\infty$ gilt $f_2(x)\to -\infty.$

Die Funktion $f_3$ kann den Graphen $G_f$ beschreiben.

1.2 Analysis

$\(\begin{array}[t]{rlll} f(x)&= & x^4-k\cdot x^2\\[5pt] f$

Anwenden der notwendigen Bedingung für Extremstellen:

$\(\begin{array}[t]{rlll} f$

Mit dem Satz vom Nullprodukt ist dies für $x_1=0$ oder $2x^2-k=0$ erfüllt.

$\begin{array}[t]{rll} 2x^2-k &= & 0 \quad \scriptsize \mid\, +k\, \mid\, :2\\[5pt] x^2 &= & \frac{k}{2} \quad \scriptsize \mid \sqrt{\,\,} \\[5pt] x_{2,3} &= & \pm \sqrt{\frac{k}{2}} \\[5pt] \end{array}$

Auf die hinreichende Bedingung kann verzichtet werden, weil aus der Aufgabe bekannt ist, dass es genau zwei Tiefpunkte gibt. Da nicht zwei Tiefpunkte aufeinander folgen können, muss bei $x_1=0$ ein Hochpunkt liegen und zwei Tiefpunkte bei $x_{2,3}$ liegen.

Es soll gelten $f \left(\sqrt{\frac{k}{2}} \right)=-1$ und $f \left(-\sqrt{\frac{k}{2}} \right)=-1.$

Für $f \left(-\sqrt{\frac{k}{2}} \right)=-1$ ergibt sich ebenfalls $k_{1,2}.$

Da $k$ eine positive reelle Zahl sein soll, folgt $k=2.$

1.3 Analysis

$\(f(x)=F$

$f(0)$ beschreibt die Steigung der Tangente an den Graphen von $F$ an der Stelle $x=0.$ Durch Einzeichnen eines Steigungsdreiecks in die Abbildung ergibt sich:

$f(0) = m_t\approx \frac{2}{1}= 2$

Mathematische Grafik mit einem Kurvenverlauf und Achsenbeschriftungen.

$\begin{array}[t]{rll} \displaystyle\int_{a}^{b}f(x)\;\mathrm dx &=& 0 \\[5pt] F(b)-F(a) &=& 0 \end{array}$

Somit müssen $F(a)$ und $F(b)$ gleich groß sein. Die Funktionswerte von $F(x)$ können in der Abbildung abgelesen werden. Ein mögliches Intervall ist $[4;7].$

Damit die Funktion $f$ an der Stelle $x_s$ monoton steigend ist, muss die Ableitungsfunktion $\(f$ an dieser Stelle größer null sein. $\(f$
Wenn $\(F$ , dann ist der Graph von $F$ an dieser Stelle linksgekrümmt. Im angegebenen Intervall ist das zum Beispiel an der Stelle $x_s=5$ der Fall.

1.4 Analysis

$f(3)=\ln(2\cdot3-5)=\ln(1)=0$

Zuerst wird die Steigung der Tangente im Punkt $P$ berechnet:

Die Ableitung von $\ln(x)$ ist $\dfrac{1}{x}.$ Damit gilt für die erste Ableitung von $f:$

$\(f$

Für die Steigung der Tangente gilt:

$\(m_t=f$

Die Normalensteigung entspricht dem negativen Kehrwert der Tangentensteigung. Somit gilt:

$m_h=-\dfrac{1}{m_t}=-\dfrac{1}{2}$

Einsetzen der Koordinaten von $S(3\mid 0)$ und $m_h$ in die allgemeine Geradengleichung:

$\begin{array}[t]{rll} h: \; y &= & m_h \cdot x + b \\[5pt] 0 &= & -\dfrac{1}{2}\cdot3+b \quad \scriptsize \; \mid \; +\frac{3}{2}\\[5pt] \frac{3}{2} &= & b \\[5pt] b &= & \frac{3}{2} \end{array}$

$h(x)=-\frac{1}{2}x+ \frac{3}{2}$

Das Dreieck, das von den beiden Koordinatenachsen und der Normalen $h$ eingeschlossen wird, ist rechtwinklig. Die Länge der Grundseite des Dreiecks entspricht der $x$ -Koordinate des Punktes $S$ und beträgt somit $3.$ Die Höhe des Dreiecks entspricht dem $y$ -Achsenabschnitt der Normalen: $y=\dfrac{3}{2}$

$A=\dfrac{1}{2}\cdot \dfrac{3}{2}\cdot3=2,25\;[\text{FE}]$

1.5 Geometrie

$E$ und $g_a$ stehen senkrecht zueinander wenn der Richtungsvektor von $g_a$ und die Normalenvektoren von $E$ parallel sind.

Ein Normalenvektor der Ebene $E$ ist $\overrightarrow{n} =\pmatrix{1\\-1\\1}.$

Der Richtungsvektor von $g_a$ ist $\pmatrix{2\\1+a\\2}.$

Damit die beiden parallel sind, muss es ein $\lambda$ geben, für welches gilt:

$\pmatrix{1\\-1\\1}\cdot \lambda=\pmatrix{2\\1+a\\2}$

Aus der ersten (und dritten) Zeile folgt $\lambda=2$ und aus der zweiten Zeile folgt $-\lambda = 1+a.$

$\begin{array}[t]{rll} -\lambda&=& 1+a \quad \scriptsize \mid\;\lambda=2 \\[5pt] -2&=& 1+a \quad \scriptsize \mid\;-1 \\[5pt] -3&=&a \\[5pt] a&=& -3 \end{array}$

Für $a=-3$ steht $g_a$ senkrecht zu $E.$

Damit $g_a$ in der Ebene $E$ liegt, muss der Richtungsvektor von $g_a$ parallel zu $E$ verlaufen und damit senkrecht zu $\overrightarrow{n}$ sein.
Skalarprodukt der beiden Vektoren bestimmen:

Vollständigen Rechenweg anzeigen

$a=3$

Für $a=3$ sind die Gerade und die Ebene also parallel.

Liegt nun zusätzlich der Stützpunkt $\left(1 \mid -2\mid 0\right)$ von $g_a$ auch in $E,$ dann liegt für $a=3$ ganz $g_a$ in $E.$

Vollständigen Rechenweg anzeigen

... $0=0$

Somit liegt die Gerade $g_a$ für $a=3$ in $E.$

1.6 Geometrie

Für die Koordinaten des Schnittpunkts von $E_a$ mit der $x$ -Achse wird $y=0$ und $z=0$ in die Ebenengleichung eingesetzt:

Vollständigen Rechenweg anzeigen

$x= \frac{6}{a}$

Der Schnittpunkt mit der $x$ -Achse hat also die Koordinaten $S_x\left( \frac{6}{a}\mid0\mid0\right).$
Für die Schnittpunkte mit der $y$ -Achse und der $z$ -Achse folgt analog mit $x=0$ und $z=0$ bzw. $x=0$ und $y=0:$

$S_y\left(0\mid\frac{6}{2+a}\mid0\right)$ und $S_z\left(0\mid0\mid-3\right)$

Daraus ergeben sich die Streckenlängen:

$\,\bigg \vert \,\overrightarrow{S_xS_y}\,\bigg \vert \,$ $= \left|\pmatrix{-\frac{6}{a} \\ \frac{6}{2+a}\\ 0} \right|$ $=\sqrt{\left(-\frac{6}{a}\right)^2+\left(\frac{6}{2+a}\right)^2 +0^2}$ $=\sqrt{\left(\frac{6}{a}\right)^2+\left(\frac{6}{2+a}\right)^2}$

$\,\bigg \vert \,\overrightarrow{S_xS_z}\,\bigg \vert \,$ $= \left|\pmatrix{-\frac{6}{a} \\ 0\\ -3} \right|$ $=\sqrt{\left(-\frac{6}{a}\right)^2+0^2+(-3)^2}$ $= \sqrt{\left(\frac{6}{a}\right)^2+9}$

$\,\bigg \vert \,\overrightarrow{S_yS_z}\,\bigg \vert \,$ $= \left|\pmatrix{0\\ -\frac{6}{2+a}\\ -3} \right|$ $=\sqrt{0^2+ \left(-\frac{6}{2+a}\right)^2+(-3)^2}$ $=\sqrt{ \left(\frac{6}{2+a}\right)^2+9}$

Gleichsetzen zweier Seitenlängen:

Vollständigen Rechenweg anzeigen

$\begin{array}[t]{rll} \,\bigg \vert \,\overrightarrow{S_xS_z}\,\bigg \vert \,&=&\,\bigg \vert \,\overrightarrow{S_yS_z}\,\bigg \vert \, \\[5pt] ... & & \\[5pt] \dfrac{36}{a^2}&=&\dfrac{36}{(2+a)^2} \\[5pt] \end{array}$

Damit diese Gleichung erfüllt ist, müsste $a=2+a$ oder $a= -(2+a)$ gelten.
Aus $a=2+a$ würde $0=2$ folgen.
Aus $a= -(2+a)$ folgt $a= -2-a$ und damit $2a = -2,$ also $a=-1.$

Da dies die einzige Lösung für $a$ ist und $a\gt 0$ vorgegeben ist gibt es somit keinen Wert für $a,$ bei dem ein gleichseitiges Dreieck zwischen den Schnittpunkten der Koordinatenachsen entsteht.

1.5 Stochastik

Vierfeldertafel anzeigen

	$B$	$\overline{B}$
$A$	$p$	$3p-p =\color{#44B350}{2p}$	$3p$
$\overline{A}$	$4p-p = \color{#44B350}{3p}$	$1-3p-3p = \color{#44B350}{1-6p}$	$1-3p$
	$4p$	$\color{#44B350}{1-4p}$	$1$

Bei $p=\dfrac{1}{5}$ ergibt sich für $1-6p$ ein Wert kleiner als $0$ . Das ist nicht möglich, da die Wahrscheinlichkeit keine negativen Werte annehmen kann.

Für zwei stochastisch unabhängige Ereignisse gilt:

$P(A\cap B)=P(A)\cdot P(B)$

Einsetzen der Werte aus der Vierfeldertafel:

$\begin{array}[t]{rll} p&=& 3p\cdot4p& \quad \scriptsize \; \\[5pt] p&=& 12p^2& \quad \scriptsize \mid\;:12p \\[5pt] \frac{1}{12}& = & p \\[5pt] p &=& \frac{1}{12} \end{array}$

Für $p=\frac{1}{12}$ sind $A$ und $B$ stochastisch unabhängig.

1.6 Stochastik

Anwenden der Pfadregeln:

$\frac{2}{10}\cdot\frac{8}{9}+\frac{8}{10}\cdot\frac{2}{9}=\frac{16}{90}+\frac{16}{90}$ $=\frac{32}{90}=\frac{16}{45}$

Mit einer Wahrscheinlichkeit von $\frac{16}{45}$ wird genau eine rote Kugel gezogen.

Die Wahrscheinlichkeit keine rote Kugel zu ziehen, lässt sich durch folgenden Term darstellen:

$\dfrac{n}{n+1}\cdot\dfrac{n-1}{n}=\dfrac{n-1}{n+1}$

Damit folgt:

Vollständigen Rechenweg anzeigen

$\begin{array}[t]{rll} \dfrac{n-1}{n+1}&\geq&0,9 \\[5pt] ...&& \\[5pt] n&\geq& 19 \\[5pt] \end{array}$

Der kleinste Wert für $n$ , bei dem die Aussage erfüllt wird, ist $19.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?