Analytische Geometrie 3.1 - Podest

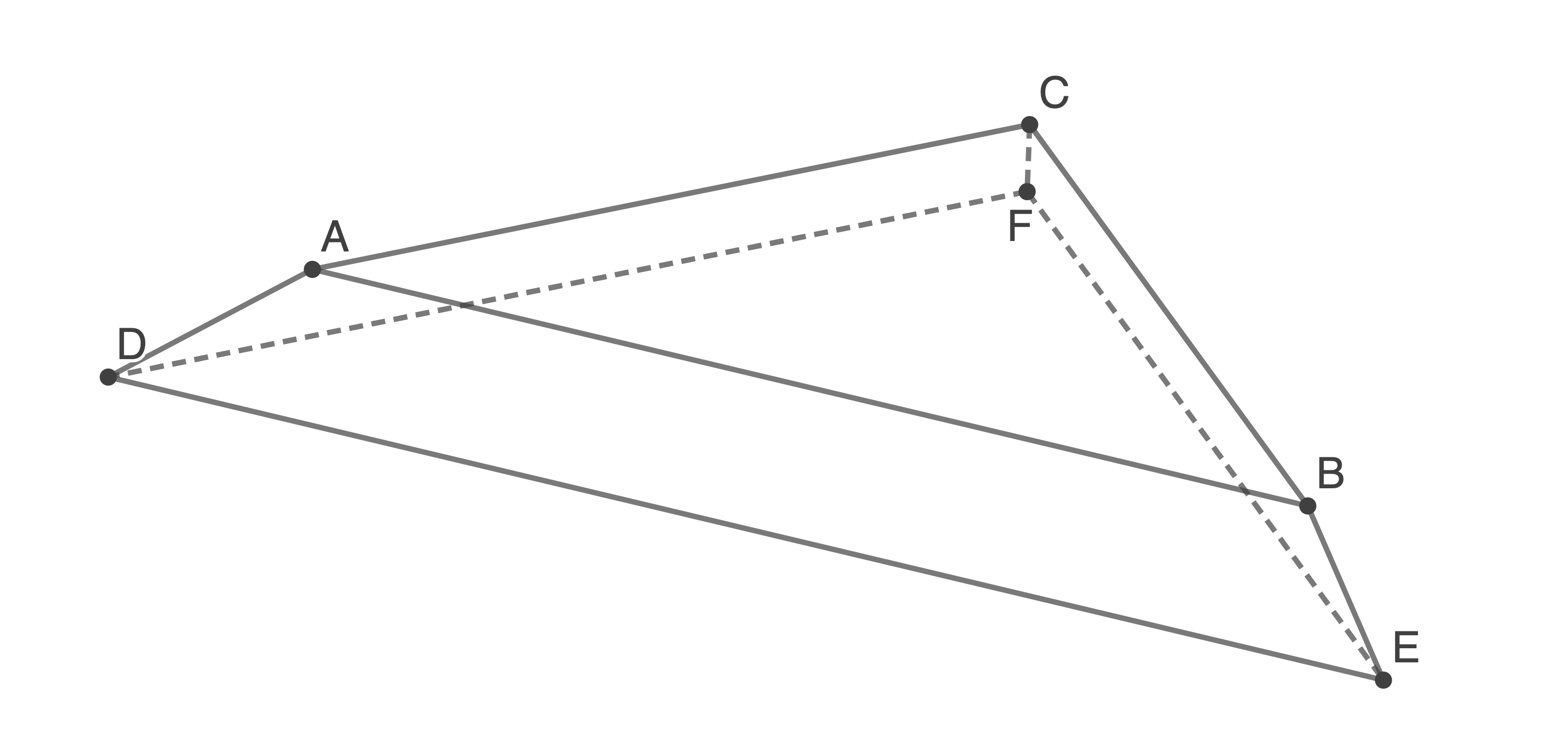
In einem Koordinatensystem wird der abgebildete Körper $ABCDEF$ mit $A(0\mid 10\mid 1),$ $B(10\mid 20\mid 1),$ $C(0\mid 20\mid 1),$ $D(0\mid 7\mid 0)$ und $F(0\mid 20\mid 0)$ betrachtet.

Die beiden Seitenflächen $ACFD$ und $BEFC$ stehen senkrecht zur $xy$ -Ebene.

Geometrische Darstellung eines Vierecks mit diagonalen Linien und Punkten A, B, C, D, E, F.

$A,B$ und $D$ liegen in der Ebene $H.$
Bestimme eine Gleichung von $H$ in Koordinatenform.

[Kontrollergebnis: $x - y + 3z + 7 = 0$ ]

(4 BE)

Begründe, dass die Gerade $i:\overrightarrow{x}=\pmatrix{0\\7\\0}+\lambda\cdot\pmatrix{1\\1\\0}$ mit $\lambda\in\mathbb{R}$ sowohl in der $xy$ -Ebene als auch in der Ebene $H$ liegt.

(2 BE)

Der Punkt $E$ liegt auf der Geraden $i,$ wobei der Abstand von $E$ zu $F$ ebenso groß ist wie der Abstand von $D$ zu $F.$

Ermittle die Koordinaten von $E.$

(5 BE)

Begründe ohne zu rechnen, dass die Vierecke $ACFD$ und $BEFC$ den gleichen Flächeninhalt haben.

(3 BE)

Der Körper $ABCDEF$ stellt modellhaft ein Podest dar, das auf der Bühne eine Theaters steht, das Viereck $ADEB$ die Vorderseite des Podests und der Punkt $D$ deren untere linke Ecke. Die $xy$ -Ebene beschreibt den horizontalen Boden der Bühne. Eine Längeneinheit im Koordinatensystem entspricht einem Meter in der Wirklichkeit.

Zeige, dass die Deckfläche des Podests rechtwinklig ist, und berechne deren Flächeninhalt.

(3 BE)

Die Position eines Scheinwerfers kann im Model durch den Punkt $\left(5 \mid -3 \mid z\right)$ dargestellt werden. Vom Scheinwerfer ausgehendes Licht trifft an der unteren linken Ecke der Vorderseite des Podests unter einem Winkel der Größe $47^{\circ}$ auf den Boden auf.
Ermittle die Höhe des Scheinwerfers über dem Boden der Bühne.

(4 BE)

Die Position eines zweiten Scheinwerfers lässt sich im Modell durch de Punkt $P\left(2 \mid 4 \mid 8\right)$ beschreiben. Die Gerade mit der Gleichung $\overrightarrow{x}=\pmatrix{0\\10\\1}+\mu\cdot\pmatrix{1\\1\\0}$ und $\mu\in\mathbb{R}$ schneidet die Ebene mit der Gleichung $\left(\overrightarrow{x}-\pmatrix{2\\4\\8}\right)\circ\pmatrix{1\\1\\0}=0$ im Punkt $Q(-2\mid 8 \mid 1).$

Es gilt $\left|\overline{PQ}\right|=9.$

Ermittle den Parameter $\mu,$ für den der Punkt $A$ auf den Punkt $Q$ abgebildet wird.
Triff auf der Grundlage des Parameters $\mu$ und der in 2.c) genannten Informationen eine Aussage über den Abstand des zweiten Scheinwerfers von der Vorderkante der Deckfläche des Podests.
Begründe deine Aussage ohne zu rechnen.

(4 BE)

(25 BE)

Ebenengleichung $H$ in Koordinatenform aufstellen:

Spannvektoren $\overrightarrow{AB}$ und $\overrightarrow{AD}$ aufstellen:

$\begin{array}[t]{rll} \overrightarrow{AB}&=& \pmatrix{10-0\\20-10\\1-1}\\[5pt] &=& \pmatrix{10\\10\\0} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{AD}&=& \pmatrix{0-0\\7-10\\0-1}\\[5pt] &=& \pmatrix{0\\-3\\-1} \end{array}$

Normalenvektor aufstellen:

Einen Normalenvektor $\overrightarrow{n}$ kannst du mit dem Kreuzprodukt von $\overrightarrow{AB}$ und $\overrightarrow{AD}$ berechnen.

$\overrightarrow{n}=\pmatrix{1\\-1\\3}$

Vollständige Lösung anzeigen

Normalenform aufstellen und in Koordinatenform umwandeln:

$\begin{array}[t]{rll} H:0&=& \pmatrix{1\\-1\\3}\circ\left[\pmatrix{x\\y\\z}-\pmatrix{0\\10\\1}\right] \\[5pt] H:0&=&x-y+10+3z+3\\[5pt] H:0&=& x-y+3z+7 \end{array}$

Eine Gleichung von $H$ in Koordinatenform ist gegeben durch $H: x-y+3z+7=0$ .

Lage der Geraden $i$ überprüfen:

Die $xy$ -Ebene kann durch die Ebenengleichung $Z: z=0$ beschrieben werden.
Für alle Punkte von der Geraden $i$ gilt $z=0$ , somit liegt $i$ in der $xy$ -Ebene.

$i$ mit $H$ schneiden:

$\begin{array}[t]{rll} \lambda-(7+\lambda)+3\cdot0+7&=& 0\\[5pt] \lambda-7-\lambda+7&=& 0\\[5pt] 0&=& 0 \end{array}$

Mit dieser Rechnung ist bewiesen, dass $i$ auch in der Ebene $H$ liegt.

Koordinaten des Punktes $E$ ermitteln:

Länge $\overline{DF}$ berechnen:

$\begin{array}[t]{rll} \overline{DF}&=&\sqrt{(0-0)^2+(20-7)^2+(0-0)^2} &\quad \\[5pt] &=&\sqrt{169}&\quad \\[5pt] &=&13&\quad \\[5pt] \end{array}$

Koordinaten des Punktes $E$ ermitteln:

Für $\lambda\neq0$ gilt:
$\begin{array}[t]{rll} \overline{FE} &=&\overline{DF} & \\[5pt] \bigg\vert\pmatrix{\lambda\\7+\lambda\\0}-\pmatrix{0\\20\\0}\bigg\vert&=& 13& \\[5pt] \sqrt{\lambda^2+(-13+\lambda)^2+(0-0)^2} &=& 13&\quad\\[5pt] \sqrt{\lambda^2+(-13+\lambda)^2}&=& 13&\\[5pt] \lambda&=& 13& \end{array}$

Setze $\lambda=13$ in die Geradengleichung $i$ ein.

$\begin{array}[t]{rll} \overrightarrow{OE}&=& \pmatrix{0\\7\\0}+13\cdot\pmatrix{1\\1\\0} \\[5pt] &=& \pmatrix{13\\20\\0} \end{array}$

Die Koordinaten des Punktes $E$ lauten $E(13|20|0)$ .

$A_{\text{Viereck}_{ACFD}}=A_{\text{Viereck}_{BEFC}}$ begründen:

Aus $d)$ folgt, dass $\overline{DF}=\overline{EF}$ gilt.
Die Grund- und Deckfläche des Körpers sind parallel zu der $xy$ -Ebene. Die beiden Vierecke sind dazu orthogonal. Daraus folgt, dass die Vierecke $ACFD$ und $BEFC$ Trapeze mit gleicher Höhe darstellen. Hinzu kommt, dass die Punkte $A, B, D$ und $E$ in einer Ebene liegen und dadurch $\overline{DF}=\overline{EF}$ und $\overline{AC}=\overline{BC}$ gelten.

Daraus folgt:
$A_{\text{Viereck}_{ACFD}}=A_{\text{Viereck}_{BEFC}}$

Deckfläche des Podests auf einen rechten Winkel überprüfen:

Die Deckfläche des Podests ist rechtwinklig, falls das Skalarprodukt zweier Verbindungsvektoren gleich Null ist.
Berechne die Verbindungsvektoren $\overrightarrow{CA}$ und $\overrightarrow{CB}$ :

$\begin{array}[t]{rll} \overrightarrow{CA}&=& \pmatrix{0-0\\10-20\\1-1} \\[5pt] &=& \pmatrix{0\\-10\\0} \end{array}$

$\begin{array}[t]{rll} \overrightarrow{CB}&=& \pmatrix{10-0\\20-20\\1-1} \\[5pt] &=& \pmatrix{10\\0\\0} \end{array}$

Berechne das Skalarprodukt der Verbindungsvektoren $\overrightarrow{CA}$ und $\overrightarrow{CB}$ :

$\pmatrix{0\\-10\\0}\circ\pmatrix{10\\0\\0}=0$

Vollständige Lösung anzeigen

Da das Skalarprodukt der Verbindungsvektoren $\overrightarrow{CA}$ und $\overrightarrow{CB}$ gleich Null ist, folgt daraus, dass die Deckfläche des Podests rechtwinklig ist.

Flächeninhalt der Deckfläche berechnen:

$\begin{array}[t]{rll} \overline{CA}&=&\sqrt{(0-0)^2+(10-20)^2+(1-1)^2} &\quad \ \\[5pt] &=&10&\quad \ \\[5pt] \overline{CB}&=&\sqrt{(10-0)^2+(20-20)^2+(1-1)^2} &\quad \ \\[5pt] &=&10 &\quad \ \\[5pt] \end{array}$

$A_{\text{Dreieck}}=\dfrac{1}{2} \cdot \text{Grundseite}\cdot \text{Höhe}$

$\begin{array}[t]{rll} A_{\text{Dreieck}_{ABC}}&=&\dfrac{1}{2} \cdot \overline{CA} \cdot \overline{CB} &\quad \\[5pt] &=&\dfrac{1}{2} \cdot 10 \cdot 10 &\quad \\[5pt] &=&50 \,[\text{m}^2]&\quad \\[5pt] \end{array}$

Der Flächeninhalt der Deckfläche des Podests beträgt $50\,\text{m}^2$ .

Höhe des Scheinwerfers über dem Boden der Bühne ermitteln:

$z\approx 12 \,[\text{m}]$

Vollständige Lösung anzeigen

Die Höhe des Scheinwerfers beträgt ungefähr $12\,\text{m}$ .

Punktprobe des Punktes $Q$ auf der Geraden durchführen:

$\begin{array}[t]{rll} \pmatrix{0\\10\\1}+\mu\pmatrix{1\\1\\0}&=&\pmatrix{-2\\8\\1} &\\[5pt] \end{array}$

Aus der ersten Zeile folgt:

$\begin{array}[t]{rll} \mu&=&-2 &\quad \\[5pt] \end{array}$

Aus der zweiten Zeile folgt:

$\begin{array}[t]{rll} 10+ \mu&=&8 & \quad \scriptsize \mid\;-10\\[5pt] \mu&=&-2 \end{array}$

Aus der dritten Zeile folgt:

$\begin{array}[t]{rll} 1&=&1 &\quad \\[5pt] \end{array}$

Die Werte für den Parameter $\mu$ stimmen überein.
Aus der Punktprobe ergibt sich, dass der Punkt $Q(-2|8|1)$ auf der Geraden liegt.

Aussage über den Abstand des zweiten Scheinwerfers von der Vorderkante der Deckfläche des Podests treffen:

Der Abstand muss größer als $9\,\text{m}$ sein.
Grund dafür ist, dass $Q$ der Fußpunkt des Lots von $P$ auf die Gerade durch die Punkte $A$ und $B$ ist. Da $Q$ nicht auf der Strecke $\overline{AB}$ liegt, ist der Abstand von der Strecke $\overline{AB}$ zu $P$ größer, als die Strecke $\overline{PQ}.$