Hilfsmittelfreier Teil

1.1 Analysis

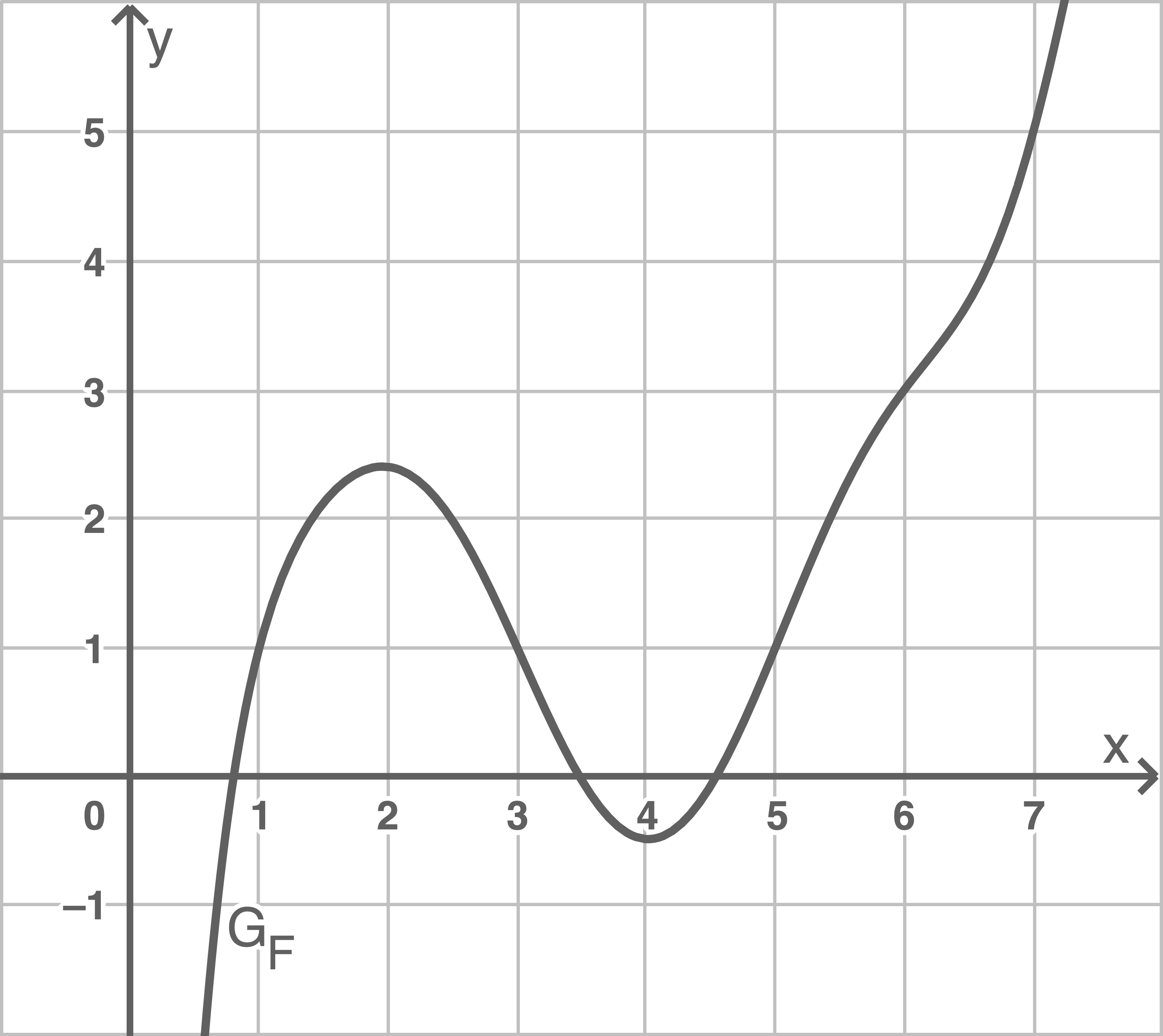
Betrachtet werden die in $\mathbb R$ definierten Funktionen $f$ und $F$ , wobei $F$ eine Stammfunktion von $f$ ist. Die Abbildung zeigt den Graphen $G_F$ von $F$ .

Bestimme den Wert des Integrals $\displaystyle\int_{1}^{7}f(x)\;\mathrm dx.$

(2 BE)

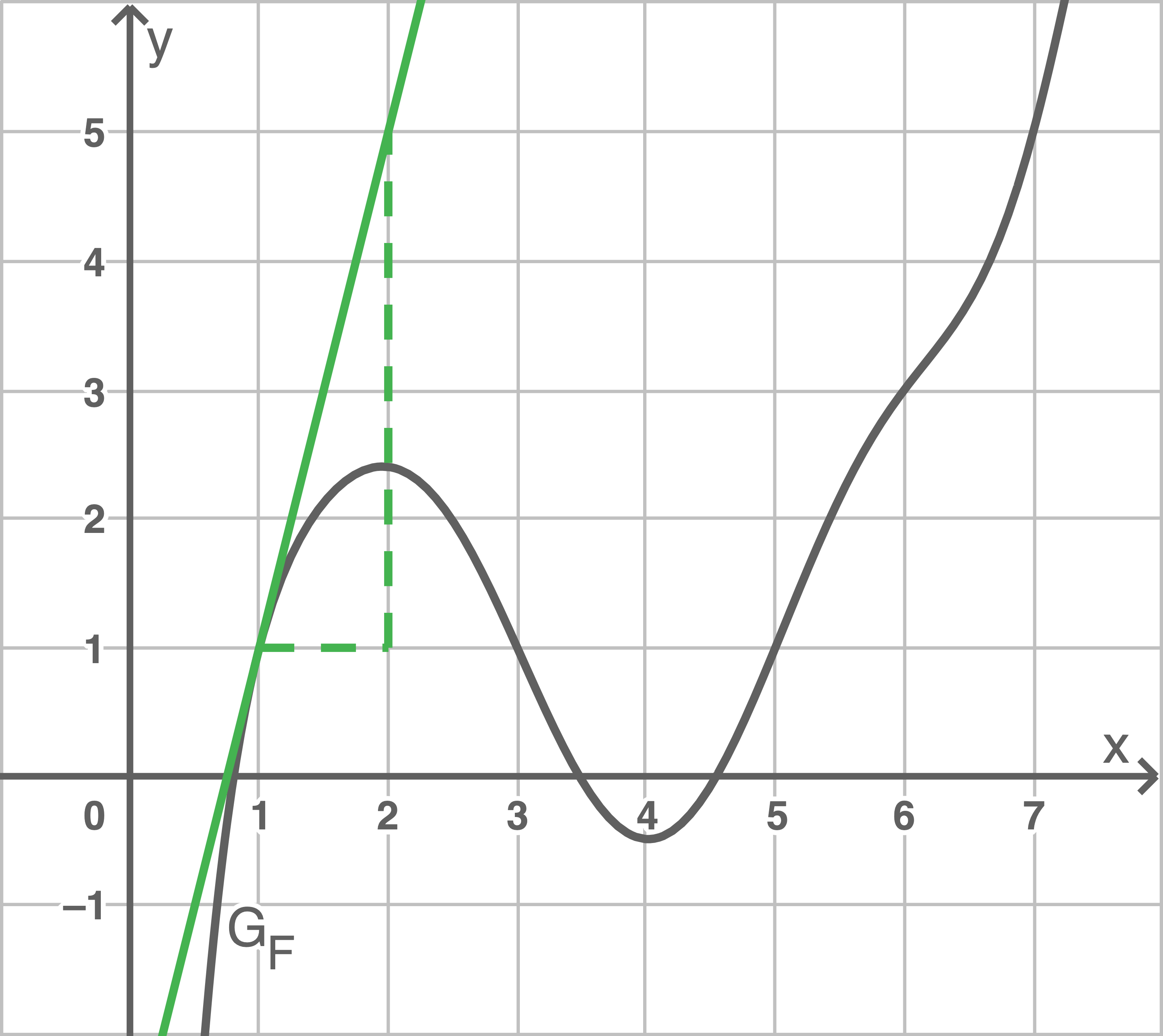
Bestimme näherungsweise den Funktionswert von $f$ an der Stelle 1. Veranschauliche dein Vorgehen in der Abbildung.

(3 BE)

funktionswert, tangente, abbildung, stammfunktion, ableitung

1.2 Analysis

Gegeben sind die in $\mathbb{R}$ definierten ganzrationalen Funktionen $f_k(x)=x^4+(2-k)\cdot x^3-k\cdot x^2$ mit $k \in \mathbb{R}.$

Begründe, dass der Graph von $f_2$ symmetrisch bezüglich der $y$ -Achse ist.

(1 BE)

Es gibt einen Wert von $k$ , für den $1$ eine Wendestelle von $f_k$ ist. Berechne diesen Wert von $k.$

(4 BE)

1.3 Analysis

Gegeben ist die in $\mathbb{R}$ definierte Funktionsschar $f_a(x)=a^2x^4+4ax^3$ ; $a \in \mathbb{R}$ ; $a>0.$

Berechne den Wert von $a,$ für den $x=-1$ eine Nullstelle von $f_a$ ist.

(1 BE)

Alle Graphen von $f_a$ haben einen von $a$ abhängigen Extrempunkt. Alle diese Extrempunkte liegen auf dem Graphen der Ortskurve $h.$ Bestimme eine Gleichung der Ortskurve $h.$

(4 BE)

1.4 Analysis

Gegeben ist die in $\mathbb{R}$ definierte Funktionenschar $f_a$ mit $f_a(x)=\mathrm e^x\cdot (1-ax)$ ; $a \in \mathbb{R}$ .

Zeige, dass $\(f$ die erste Ableitung von $f_a$ ist.

(2 BE)

Untersuche, für welche Werte des Parameters $a$ der Graph von $f_a$ eine waagerechte Tangente besitzt.

(3 BE)

1.5 Analytische Geometrie

Gegeben sind die Gerade $g:\overrightarrow x=\pmatrix{7\\3\\3}+r\cdot \pmatrix{3\\0\\-1}$ mit $r \in \mathbb{R}$ und die Ebene $E:3x-z=-2.$

Begründe, dass $g$ senkrecht zu $E$ steht.

(1 BE)

Die Gerade $h:\overrightarrow x= \pmatrix{7\\3\\3}+s\cdot \pmatrix{1\\2\\3}$ mit $s \in \mathbb{R}$ hat mit $E$ keinen gemeinsamen Punkt. Es gibt Geraden, die in $E$ liegen und parallel zu $h$ verlaufen. Bestimme eine Gleichung derjenigen dieser Geraden, die von $h$ den kleinsten Abstand hat.

(4 BE)

1.6 Analytische Geometrie

Gegeben ist die Ebenenschar $E_{a,b}:(2_a-1)x+by-z=1;$ $a,b \in \mathbb{R}$ .

Prüfe, ob $F:3x+3y=1+z$ zur Ebenenschar $E_{a,b}$ gehört.

(2 BE)

Bestimme eine Gleichung für die Geradenschar $g_b,$ die die Schnittgeraden der Ebenen $E_{a,b}$ mit der $yz$ -Ebene enthält.

(3 BE)

1.5 Stochastik

In einer Urne befinden sich schwarze (s) und weiße (w) Kugeln. Ohne Zurücklegen wird zweimal nacheinander genau eine Kugel gezogen. Für das Zufallsexperiment gilt das untenstehende unvollständige Baumdiagramm.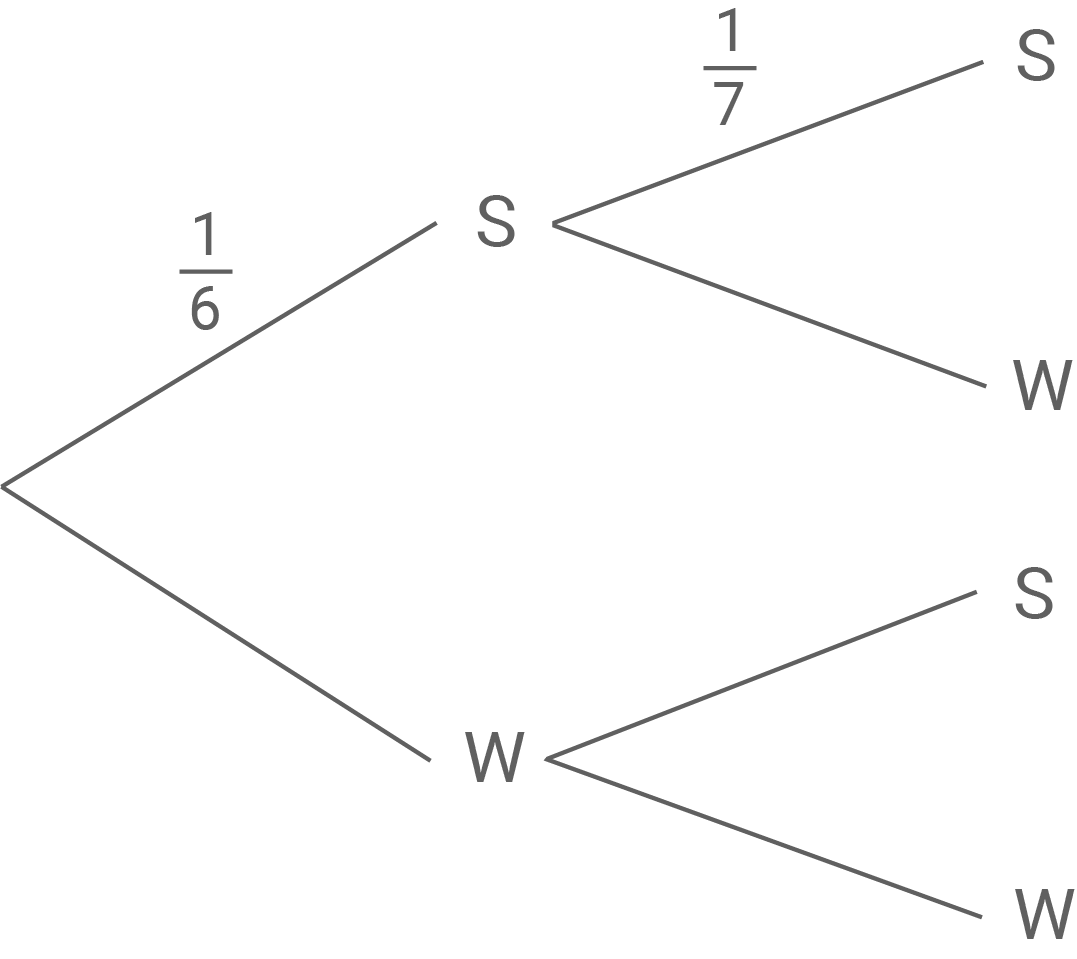

berlin mathe abi lk wtr 2022 hilfsmittelfreier teil baumdiagramm

Berechne die Wahrscheinlichkeit dafür, dass mindestens eine weiße Kugel gezogen wird.

(1 BE)

Ermittle die Anzahl der weißen und der schwarzen Kugeln, die sich vor dem Ziehen in der Urne befanden.

(4 BE)

1.6 Stochastik

Gegeben ist eine Zufallsgröße $X,$ die die Werte $x_i \in \{0,1,2,3,4\}$ annehmen kann. Die Wahrscheinlichkeitsverteilung von $X$ ist symmetrisch.

Es gilt $P(X=2)=0,6.$
Bestimme $P(X\leq2).$

(2 BE)

Weise nach, dass die Zufallsgröße $X$ nicht binomialverteilt sein kann.

(3 BE)

(30 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

1.1 Analysis

An $G_F$ können die Funktionswerte an den Stellen $x=1$ und $x=7$ abgelesen werden:

$\begin{array}[t]{rll} \displaystyle\int_{1}^{7}f(x)\;\mathrm dx&=& F(7)-F(1)&\ \\[5pt] &=& 5-1&\ \\[5pt] &=& 4 \; [\text{FE}] \end{array}$

$\(f(1)=F$

Bestimmung von $\(F$ durch das Einzeichnen der Tangente am Punkt $(1\mid1)$ :

Durch das Ablesen der Tangentensteigung ergibt sich: $\(F$

1.2 Analysis

Der Funktionsterm von $f _2$ enthält nur Potenzen von $x$ mit geraden Exponenten.

1. Schritt: Ableitungen bilden

$\(f_k$

2. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} f_k$

Auf die Anwendung der hinreichenden Bedingung für Wendestellen kann verzichtet werden, da gegeben ist, dass eine Wendestelle existiert.

1.3 Analysis

$\begin{array}[t]{rll} f_a(-1)&=& 0 \\[5pt] a^2-4 a&=&0 \\[5pt] a\cdot (a-4)&=&0 \end{array}$

Für $a=4$ ist $x=-1$ eine Nullstelle von $f_a.$

1. Schritt: Extremstelle bestimmen

Es gilt: $\(f_a$

Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_a$

Anwendung des Satzes vom Nullprodukt: $4ax^2=0$ oder $ax+3=0.$ Da $a \gt 0$ gilt, folgt:

$\begin{array}[t]{rll} ax+3&=& 0 &\quad \scriptsize \mid\;-3 \;\mid\;:a \\[5pt] x&=& -\dfrac{3}{a} \end{array}$

Auf die Anwendung der hinreichenden Bedingung für Extremstellen kann verzichtet werden, da in der Aufgabe gegeben ist, dass alle Graphen von $f_a$ einen von $a$ abhängigen Extrempunkt haben.

Der von $a$ abhängige Extrempunkt liegt also an der Stelle $x=-\dfrac{3}{a}.$

2. Schritt: Ortskurve $h$ bestimmen

Um die Ortskurve zu berechnen, muss der $x$ -Wert nach $a$ umgestellt und in $f_a$ eingesetzt werden:

$\begin{array}[t]{rll} x&=& -\dfrac{3}{a} \quad \scriptsize \mid\; \cdot a \\[5pt] ax&=& -3 \quad \scriptsize \mid\; :x \\[5pt] a&=& -\dfrac{3}{x} \end{array}$

Einsetzen in $f_a$ liefert:

Rechenweg anzeigen

$h(x)=-3x^2$

Die Gleichung der Ortskurve ist gegeben durch $h(x)=-3x^2.$

1.4 Analysis

Mit der Produktregel gilt:

$\(\begin{array}[t]{rll} f$

Damit der Graph von $f_a$ eine waagrechte Tangente besitzt, muss $\(f_a$ gelten.

$\(\begin{array}[t]{rll} f_a$

Nach dem Satz vom Nullprodukt ist die Gleichung genau dann erfüllt, wenn einer der beiden Faktoren gleich null ist. Da $\mathrm e^x \gt 0$ für alle $x \in \mathbb R$ muss gelten:

$\begin{array}[t]{rll} 1-ax-a&=& 0 \quad \scriptsize \mid\; +ax \\[5pt] 1-a&=& ax \quad \scriptsize \mid\; :a \\[5pt] \dfrac{1-a}{a} &=& x \\[5pt] x &=& \dfrac{1-a}{a} \end{array}$

Der Term ist für $a=0$ nicht definiert. Der Graph von $f_a$ besitzt also für alle $a\neq 0$ eine waagrechte Tangente.

1.5 Analytische Geometrie

Ein Normalenvektor von $E$ ist gegeben durch $\overrightarrow{n_E}=\pmatrix{3\\0\\-1}.$ Dieser stimmt mit dem Richtungsvektor von $g$ überein. Damit steht $g$ senkrecht zu $E.$

Gesucht ist eine Gerade, die durch den Schnittpunkt von $E$ und $g$ verläuft und parallel zu $h$ ist.

1. Schritt: Schnittpunkt bestimmen

Koordinaten der Geraden in die Ebenengleichung einsetzen:

$\begin{array}[t]{rll} 3\cdot (7+3r)-(3-r)&=& -2 \\[5pt] 18+10r&=& -2 \quad \scriptsize \mid\; -18 \\[5pt] 10r&=& -20 \quad \scriptsize \mid\; :10 \\[5pt] r&=& -2 \end{array}$

Einsetzen in die Geradengleichung von $g$ liefert den Schnittpunkt $S(1\mid 3 \mid 5).$

2. Schritt: Geradengleichung aufstellen

Der Schnittpunkt $S$ ist der Stützvektor der gesuchten Gerade. Da diese parallel zu $h$ verlaufen soll, hat sie den gleichen Richtungsvektor. Die gesuchte Geradengleichung lautet:

$\overrightarrow{x}= \pmatrix{1\\3\\5}+s\cdot \pmatrix{1\\2\\3}$

1.6 Analytische Geometrie

Der Vergleich der Koeffizienten von $x$ ergibt:

$\begin{array}[t]{rll} 2a-1&=& 3 &\quad \scriptsize \mid\; +1 \\[5pt] 2a&=& 4 &\quad \scriptsize \mid\; :2 \\[5pt] a &=& 2 \end{array}$

Der Koeffizientenvergleich von $y$ ergibt sofort $b=3.$

Diese Werte in $E_{a,b}$ eingesetzt ergeben:

$\begin{array}[t]{rll} (2\cdot 2-1)x+3y-z&=& 1 \\[5pt] 3x+3y-z&=& 1 \quad \scriptsize \mid\; +z \\[5pt] 3x+3y &=& 1+z \end{array}$

Dies entspricht der Ebenengleichung von $F.$ Damit gehört $F$ zur Ebenenschar $E_{a,b}.$

Für die $yz$ -Ebene gilt: $x=0$

Für die Schnittgeraden muss daher gelten: $x=0$ und $b \cdot y-z=1.$

Zum Beispiel mit $y=r$ folgt: $z=b \cdot r-1.$

$g_b: \vec{x}=\left(\begin{array}{c}0 \\ 0 \\ -1\end{array}\right)+r \cdot\left(\begin{array}{l}0 \\ 1 \\ b\end{array}\right) ; r \in R$ ist eine Gleichung der Geradenschar.

1.5 Stochastik

$P(E)=1-P(S S)=1-\dfrac{1}{6} \cdot \dfrac{1}{7}$ $=\dfrac{41}{42}$

Die Variable $s$ bezeichnet die Anzahl der schwarzen Kugeln, die Variable $a$ die Anzahl aller Kugeln.

Die Wahrscheinlichkeit, im ersten Zug eine schwarze Kugel zu ziehen, beträgt $\dfrac{1}{6}.$ Es muss also $\dfrac{s}{a}=\dfrac{1}{6}$ gelten, daraus folgt $a=6s.$

Wenn im ersten Zug eine schwarze Kugel gezogen wurde, gilt für den zweiten Zug $\dfrac{s-1}{a-1}=\dfrac{1}{7}.$ Daraus folgt $7(s-1)=a-1.$

Einsetzen von $a=6s$ liefert:

$\begin{array}[t]{rll} 7(s-1)&=& 6s-1 \\[5pt] 7s-7&=& 6s-1 \quad \scriptsize \mid\; +7 \\[5pt] 7s&=& 6s+6 \quad \scriptsize \mid\; -6s \\[5pt] s&=& 6 \end{array}$

Die Gesamtzahl der Kugeln ist folglich gegeben durch $a=6s=6\cdot 6=36.$

Vor dem Ziehen befanden sich $6$ schwarze und $36-6=30$ weiße Kugeln in der Urne.

1.6 Stochastik

Aus der Eigenschaft der Symmetrie ergibt sich:

$\begin{aligned} &P(X=0)+P(X=1)=\frac{1-0,6}{2}=0,2 \\ &P(X \leq 2)=0,2+0,6=0,8 \end{aligned}$

Annahme: Die Zufallsgröße $X$ ist binomialverteilt mit $n=4$ und $p=0,5$ (Symmetrie)

$\begin{aligned} &P(X=0)=0,5^4=\frac{1}{16} \\ &P(X=1)=\left(\begin{array}{l}4 \\1 \end{array}\right) \cdot 0,5 \cdot 0,5^3=4 \cdot 0,5^4=\frac{1}{4} \\ &P(X=0)+P(X=1)=\frac{5}{16} \end{aligned}$

Da die Wahrscheinlichkeitsverteilung der Zufallsgröße $X$ symmetrisch ist und $P(X=2)=0,6$ , müsste $P(X=0)+P(X=1)=0,2$ sein. Dies ist nicht erfüllt. Die Zufallsgröße $X$ ist nicht binomialverteilt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?