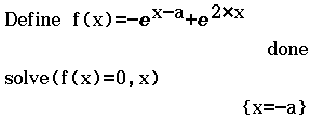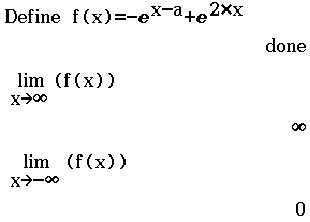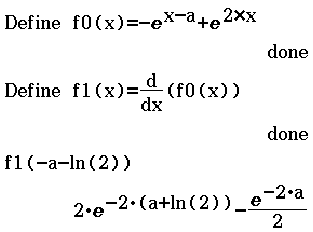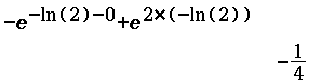Analysis 2.2
Bremsschuh
Gegeben ist die Funktionenschar
a)
Ermittle die Koordinaten der Schnittpunkte von  mit den beiden Koordinatenachsen in Abhängigkeit von
mit den beiden Koordinatenachsen in Abhängigkeit von  .
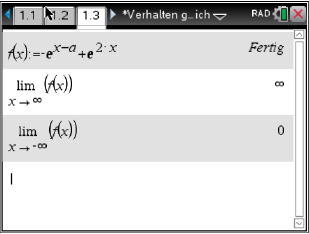
Gib das Verhalten der Funktionswerte von
.
Gib das Verhalten der Funktionswerte von  für
für  und
und  an.
an.
(5P)
b)
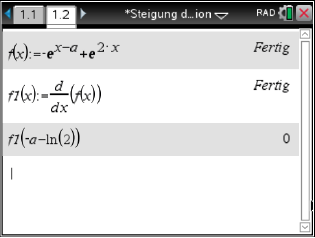
Weise nach, dass jeder Graph  im Punkt
im Punkt  eine zur
eine zur  -Achse parallele Tangente besitzt.
Zeig, dass
-Achse parallele Tangente besitzt.
Zeig, dass  ein lokaler Extrempunkt von
ein lokaler Extrempunkt von  ist.
Bestimme dessen Koordinaten sowie die Art des Extremums.
ist.
Bestimme dessen Koordinaten sowie die Art des Extremums.
(8P)
c)
Genau ein Graph  hat einen Wendepunkt an der Stelle
hat einen Wendepunkt an der Stelle  .
Berechne den Abstand dieses Wendepunktes zum Koordinatenursprung
.
Berechne den Abstand dieses Wendepunktes zum Koordinatenursprung  .
.
(5P)
d)
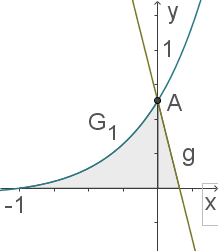
Der Graph  und die Gerade
und die Gerade  mit der Gleichung
mit der Gleichung  begrenzen gemeinsam mit der
begrenzen gemeinsam mit der  -Achse eine Fläche, die dem Querschnitt eines Bremsschuhs entspricht, der das Wegrollen von Fahrzeugen verhindert (
-Achse eine Fläche, die dem Querschnitt eines Bremsschuhs entspricht, der das Wegrollen von Fahrzeugen verhindert ( ).
Die „Tiefe“ des Bremsschuhs beträgt
).
Die „Tiefe“ des Bremsschuhs beträgt  .
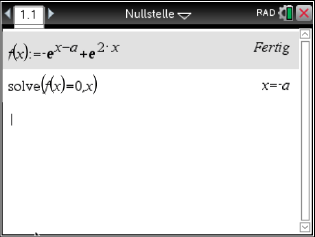
Zeig, dass sich
.
Zeig, dass sich  und
und  auf der
auf der  -Achse schneiden.
Berechne das Volumen eines solchen Bremsschuhs.
-Achse schneiden.
Berechne das Volumen eines solchen Bremsschuhs.
(12P)
e)
Ermittle die Größe des Winkels, den  und
und  im Punkt
im Punkt  einschließen.
einschließen.
(5P)
f)
Der Produzent der Bremsschuhe möchte auf der Querschnittsfläche des Bremsschuhs sein rechteckiges Firmenlogo mit den Seitenlängen  und
und  so einstanzen lassen, dass die längere der beiden Seiten parallel zur
so einstanzen lassen, dass die längere der beiden Seiten parallel zur  -Achse verläuft.
Untersuche, ob das möglich ist.
-Achse verläuft.
Untersuche, ob das möglich ist.
(5P)
Bildnachweise [nach oben]
© 2016 - SchulLV.
Aufgabe 1.2: Bremsschuh
a)
b)
Hinreichende Bedingung:
 Abb. 4: Bestimmung des Extrempunkts
Abb. 4: Bestimmung des Extrempunkts
Hinreichende Bedingung Hochstelle:
c)
 Abb. 6: Bestimmung der Koordinaten des Wendepunkts
Abb. 6: Bestimmung der Koordinaten des Wendepunkts
d)
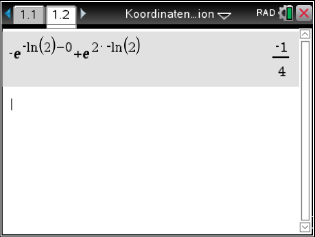
 Abb. 7: Bestimmung des Integrals
Abb. 7: Bestimmung des Integrals
e)
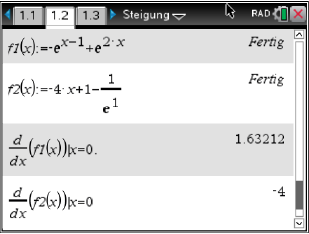 Abb. 8: Bestimmung der Steigung
Abb. 8: Bestimmung der Steigung
f)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
Aufgabe 1.2: Bremsschuh
a)
b)
Hinreichende Bedingung:
 Abb. 4: Bestimmung des Extrempunkts
Abb. 4: Bestimmung des Extrempunkts
Hinreichende Bedingung Hochstelle:
c)
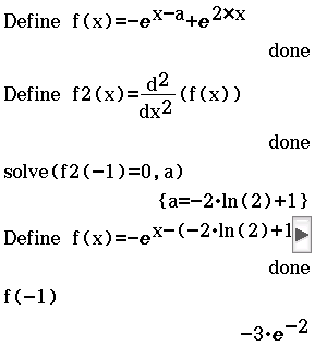 Abb. 6: Bestimmung der Koordinaten des Wendepunkts
Abb. 6: Bestimmung der Koordinaten des Wendepunkts
d)
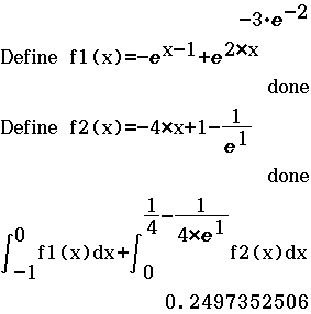 Abb. 7: Bestimmung des Integrals
Abb. 7: Bestimmung des Integrals
e)
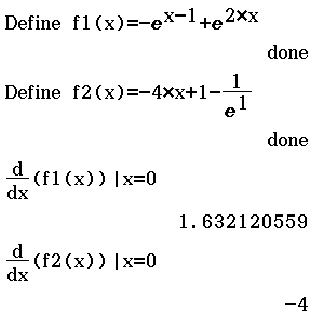 Abb. 8: Bestimmung der Steigung
Abb. 8: Bestimmung der Steigung
f)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.