Analysis 2.1 - Brücke

Analysis: Brücke

Die folgende Abbildung zeigt modellhaft den Längsschnitt einer dreiteiligen Brücke aus Holz für eine Spielzeugeisenbahn. Die Züge können sowohl über die Brücke fahren als auch darunter hindurch.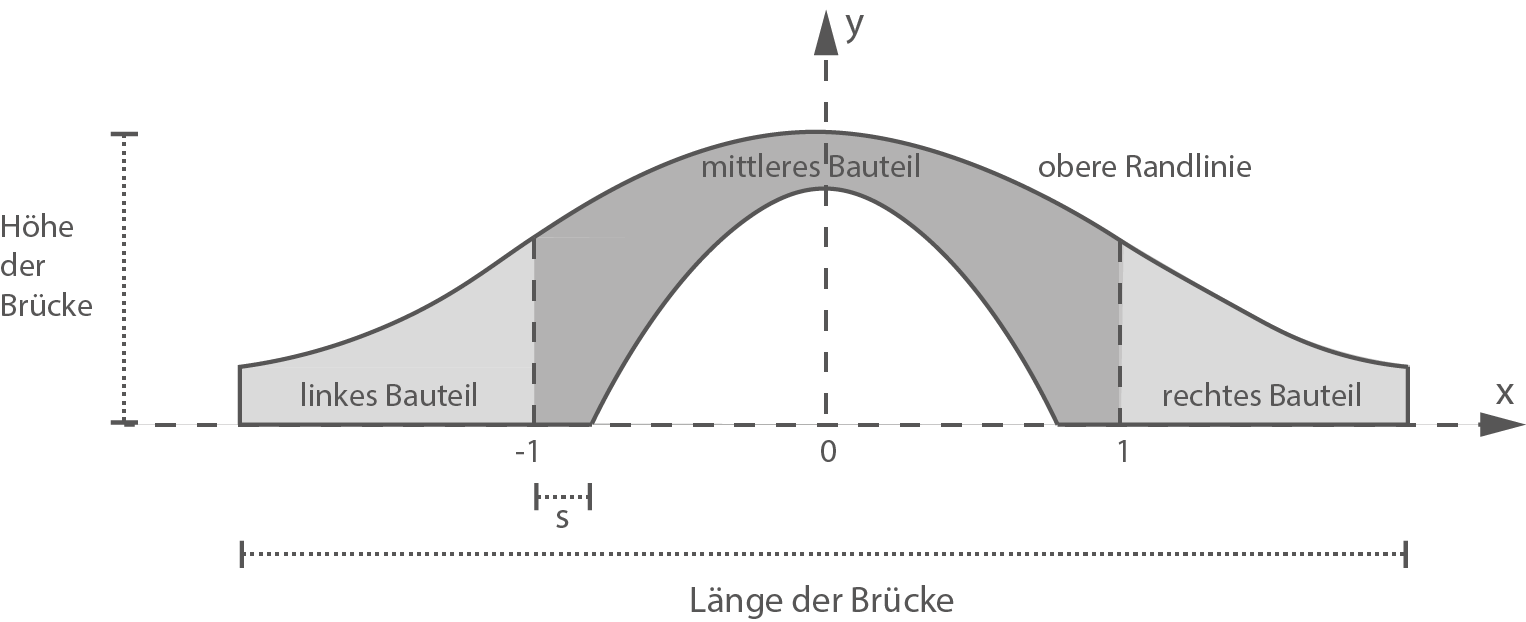

Grafik einer Brücke mit Höhe und Bauteilen, beschriftet mit

Die obere Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen der in $\mathbb{R}$ definierten Funktion $f$ mit $f(x)= \frac{1}{20}x^4 -\frac{2}{5}x^2 +1$ beschrieben werden.
Dabei werden die Endpunkte dieser Randlinie durch die beiden Tiefpunkte des Graphen von $f$ dargestellt. Im verwendeten Koordinatensystem beschreibt die $x$ -Achse die Horizontale; eine Längeneinheit entspricht einem Dezimeter in der Realität.

Zeige rechnerisch, dass die obere Randlinie achsensymmetrisch ist.

(2 BE)

Bestimme rechnerisch die Höhe und die Länge der Brücke.
(zur Kontrolle: Ein Tiefpunkt des Graphen von $f$ hat die x-Koordinate 2.)

(4 BE)

Betrachtet wird derjenige Punkt der oberen Randlinie, der sich am Übergang vom mittleren zum rechten Bauteil befindet.
Prüfe, ob dieser Punkt auf halber Höhe zwischen dem höchsten Punkt der oberen Randlinie und deren rechtem Endpunkt liegt.

(3 BE)

Gib die Bedeutung des Terms $\dfrac{f(2)-f(1)}{2-1}$ im Sachzusammenhang an und berechne seinen Wert.

(2 BE)

Berechne die Größe des größten Steigungswinkels der Brücke, der beim Überfahren zu überwinden ist.

(4 BE)

Der parabelförmige Teil der unteren Randlinie des Längsschnitts der Brücke kann mithilfe des Graphen einer in $\mathbb{R}$ definierten Funktion $q$ mit $q(x)= 0,8 -a\cdot x^2;$ $a\in \mathbb{R},$ $a\gt 0$ beschrieben werden.

In der Abbildung ist die Länge einer der beiden Bodenflächen des mittleren Bauteils mit $s$ bezeichnet.
Bestimme alle Werte von $a,$ die für diese Länge mindestens 0,1 dm liefern.

(4 BE)

Begründe im Sachzusammenhang, dass für die Beschreibung der unteren Randlinie beliebig große Werte von $a$ nicht infrage kommen.

(2 BE)

Für die Brücke gilt $a = 1,25 .$ Die drei Bauteile der Brücke werden aus massivem Holz hergestellt; $1 \,\text{dm}^3$ des Holzes hat eine Masse von 800 Gramm. Die Brücke ist 0,4 dm breit.
Ermittle die Masse des mittleren Bauteils.

(5 BE)

Während der Planung der Brückenform kamen zur Beschreibung der oberen Randlinie für das linke Bauteil eine Funktion $g_l$ und für das rechte Bauteil eine Funktion $g_r$ infrage. Auch bei Verwendung dieser Funktionen wäre die obere Randlinie achsensymmetrisch gewesen. Beurteile jede der folgenden Aussagen, ob sie zutreffend ist oder nicht:

$-g_l(x)= g_r(-x)$ für $-2 \leq x \leq -1$

$g_l(x-1)= g_r(-x+1)$ für $-1 \leq x \leq 0$

(4 BE)

Die Funktion $f$ ist eine Funktion der Funktionenschar $h_k$ mit der Gleichung $h_k(x)= \frac{k}{40}x^4 - \frac{10-k}{20}x^2 +1;$ $x,k \in \mathbb{R}.$ Ihre Graphen werden mit $G_k$ bezeichnet.

Weise nach, dass der Graph der Funktion $f$ (aus Aufgabe 1) ein Graph der Schar $G_k$ ist.

(2 BE)

Begründe, dass alle Graphen der Schar $G_k$ einen Punkt gemeinsam haben.

(2 BE)

Ermittle die Anzahl und die Art der relativen Extrema der Graphen $G_k$ für die beiden Fälle $k\gt 10$ und $k\leq 0 .$

(4 BE)

Für einen Graphen $G_k$ mit $\dfrac{9}{5} \lt k \lt 10$ gelten folgende Bedingungen:

Die $y$ -Koordinate eines lokalen Extrempunktes ist $y=-\dfrac{1}{40}k + \dfrac{3}{2}-\dfrac{5}{2k}.$
Die Summer der vertikalen Abstände der lokalen Extrempunkte von $G_k$ zur $x$ -Achse beträgt $1,4 \text{LE}.$

Ermittle den zugehörigen Parameterwert für $k.$

(4 BE)

Es gibt einen Wert $k$ mit $0 \lt k \lt 10,$ für den der Graph von $h_k$ genau zwei Schnittpunkte mit der $x$ -Achse hat.
Weise nach, dass dieser Wert für $k$ Lösung der Gleichung $(10-k)^2 = 40k$ ist.

(6 BE)

Entscheide, ob folgende Aussage wahr ist, und begründe deine Entscheidung.

Besitzt ein Graph der Schar $G_k$ einen Schnittpunkt mit der $x$ -Achse, so kann man auf Grund seiner Symmetrie zur $y$ -Achse daraus schlussfolgern, dass ein weiterer Schnittpunkt mit der $x$ -Achse existiert.

(2 BE)

(50 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Aufgabe 2.1: Brücke CAS

Damit eine Funktion $f(x)$ achsensymmetrisch ist, muss gelten:

$f(x)=f(-x)$

$\dfrac{1}{20}x^4-\dfrac{2}{5}x^2+1$ $=\dfrac{1}{20}(-x)^4-\dfrac{2}{5}(-x)^2+1$

Höhe: Im Schaubild ist zu sehen, dass der Hochpunkt an der Stelle $x=0$ liegt:

$f(0)=0-0+1=1$

$H(0\mid1)$

Die Höhe der Brücke beträgt $10\;\text{cm}.$

Länge: Bestimmung der lokalen Minima:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 6: Graph analysieren $\to$ 2: Minimum

$\blacktriangleright$ Casio Classpad II

Analyse $\to$ Grafische Lösung $\to$ Minimum

Die beiden lokalen Minima liegen bei $x=-2$ und $x=2.$
Somit beträgt die Länge der Brücke $4\;\text{dm}=40\;\text{cm}.$

Höhe des Übergangspunktes zwischen mittlerem und letztem Bauteil:

$f(1)=\dfrac{1}{20}-\dfrac{2}{5}+1=\dfrac{13}{20}=0,65$

Halbe Höhe zwischen dem höchsten Punkt der oberen Randlinie und deren rechtem Endpunkt:

$\dfrac{f(0)+f(2)}{2}=\dfrac{1+0,2}{2}=0,6$

$0,65\neq0,6$

Der Term gibt die mittlere Steigung der oberen Randlinie des rechten Bauteils an.

$\dfrac{f(2)-f(1)}{2-1}=0,2-0,65=-0,45$

Um die maximale Steigung zu berechnen muss die Ableitung zweiten Grades gleich null gestzt werden:

$\(f$
$\dfrac{3}{5}x^2-\dfrac{4}{5}=0$
$3x^2=4\quad x_{1/2}=\sqrt{\dfrac{4}{3}}$
Die maximale Steigung ist $\(f$
$\alpha=31,63°$

$q(x)$ muss an der Stelle $x=-0,9(0,1-1)$ mindestens null sein:

$q(-0,9)\leq0$
$0,8-a\cdot(-0,9)^2\leq0$
$0,81a\geq0,8$

$a\geq\dfrac{80}{81}$

Die Werte von $a$ beschreiben die Breite der Durchfahrt der Brücke. Für große Werte von $a$ wird die Durchfahrt schmaler. Somit kann $a$ nicht beliebig groß werden. Die Durchfahrt wird sonst zu eng für die Züge.

Zunächst wird der Inhalt der Fläche, die von den Graphen der Funktionen $f(x)$ und $q(x)$ eingeschlossen ist, berechnet.
Die Nullstellen von $q_{1,25}(x)$ liegen bei $x=\pm0,8.$

Da nur der Inhalt der Fläche des mittleren Bauteils berechnet wird, werden dazu die bestimmten Integrale verwendet.

$\displaystyle\int_{-1}^{1}f(x)\;\mathrm dx-\displaystyle\int_{-0,8}^{0,8}q(x)\;\mathrm dx$ $=1,753-0,853=0,9$

Das Volumen des Teils beträgt: $0,9\,\text{dm}^2\cdot0,4\,\text{dm}=0,36\,\text{dm}^3$

$m=V\cdot\rho=0,36\,\text{dm}^3\cdot800\dfrac{g}{\text{dm}^3}$ $=288\,\text{g}$

Aufgabe 2

Die erste Aussage ist nicht korrekt, da die Funktionen $g_l$ und $g_r$ nicht punktsymmetrisch zum Ursprung sein dürfen.

Die zweite Ausage ist korrekt. Die beiden Funktionen sind zueinander symmetrisch zur $y$ -Achse. Es gilt: $g_l(x)=g_r(-x)$

Aufgabe 3

$f(x)=h_k(x)$

$\dfrac{1}{20}x^4-\dfrac{2}{5}x^2+1$ $=\dfrac{k}{40}x^4-\dfrac{10-k}{20}x^2+1$

Es fällt auf, dass die Gleichung für $k=2$ erfüllt ist.

$\dfrac{1}{20}x^4-\dfrac{2}{5}x^2+1$ $=\dfrac{2}{40}x^4-\dfrac{10-2}{20}x^2+1$

Für $x=0$ gilt immer $h_k(x)=1$ .

Somit besitzen alle Graphen der Funktionenschar den Punkt $P(0\mid1).$

$\(h_k$
$\(h_k$

Hinreichendes Kriterium für Extremstellen:

$\(h_k$
$x_1=0\quad x_{2/3}=\pm\sqrt{\dfrac{10-k}{k}}$

Für $k\gt10$ und $k\leq0$ können sich nur Extrema bei $x=0$ bilden, da für diese Werte von $k$ die Nullstellen $x_{2/3}$ kein Ergebnis liefern. Unter der Wurzel können keine negativen Werte stehen.

Für $k\gt10$ gilt $\(h_k$ Alle Graphen $G_k$ mit $k\gt10$ haben somit einen Tiefpunkt bei $x=0.$
Für $k\leq0$ gilt $\(h_k$ Alle Graphen $G_k$ mit $k\leq0$ haben somit einen Hochpunkt bei $x=0.$

$h_k(x)=0$

$\dfrac{k}{40}x^4-\dfrac{10-k}{20}x^2+1=0$

Substitution: $x^2=z$

$\dfrac{k}{40}z^2-\dfrac{10-k}{20}z+1=0$
$z^2-\dfrac{20-2k}{k}z+\dfrac{40}{k}=0$

pq-Formel:

$z_{1/2}=\dfrac{10-k}{k}\pm\sqrt{\left(\dfrac{10-k}{k}\right)^2-\dfrac{40}{k}}$

Da $z=x^2$ und da für $x$ genau zwei Lösungen gesucht werden, muss die Wurzel gleich null gestzt werden:

$\sqrt{\left(\dfrac{10-k}{k}\right)^2-\dfrac{40}{k}}=0$
$\left(\dfrac{10-k}{k}\right)^2=\dfrac{40}{k}$

$(10-k)^2=40k$

Die Aussage ist wahr. Der Graph $G_k$ ist für alle $k$ symmetrisch zur $y$ -Achse. Wenn es einen Schnittpunkt mit der $x$ -Achse gibt, der nicht bei $x=0$ ist, muss es einen weiteren Schnittpunkt mit der $x$ -Achse geben.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?