Analysis 2.2 - Exponentialfunktion
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit  . Die zugehörigen Graphen sind symmetrisch bezüglich des Kooridnatenursprungs.
. Die zugehörigen Graphen sind symmetrisch bezüglich des Kooridnatenursprungs.
1.
Zunächst werden einzelne Funktionen der Schar betrachtet.
a)
Gib die Koordinaten des Hochpunkts des Graphen von  an.
an.
Weise nach, dass genau eine Nullstelle hat, und gib den Grenzwert von
genau eine Nullstelle hat, und gib den Grenzwert von  für
für  an.
an.
Weise nach, dass
(3 BE)
b)
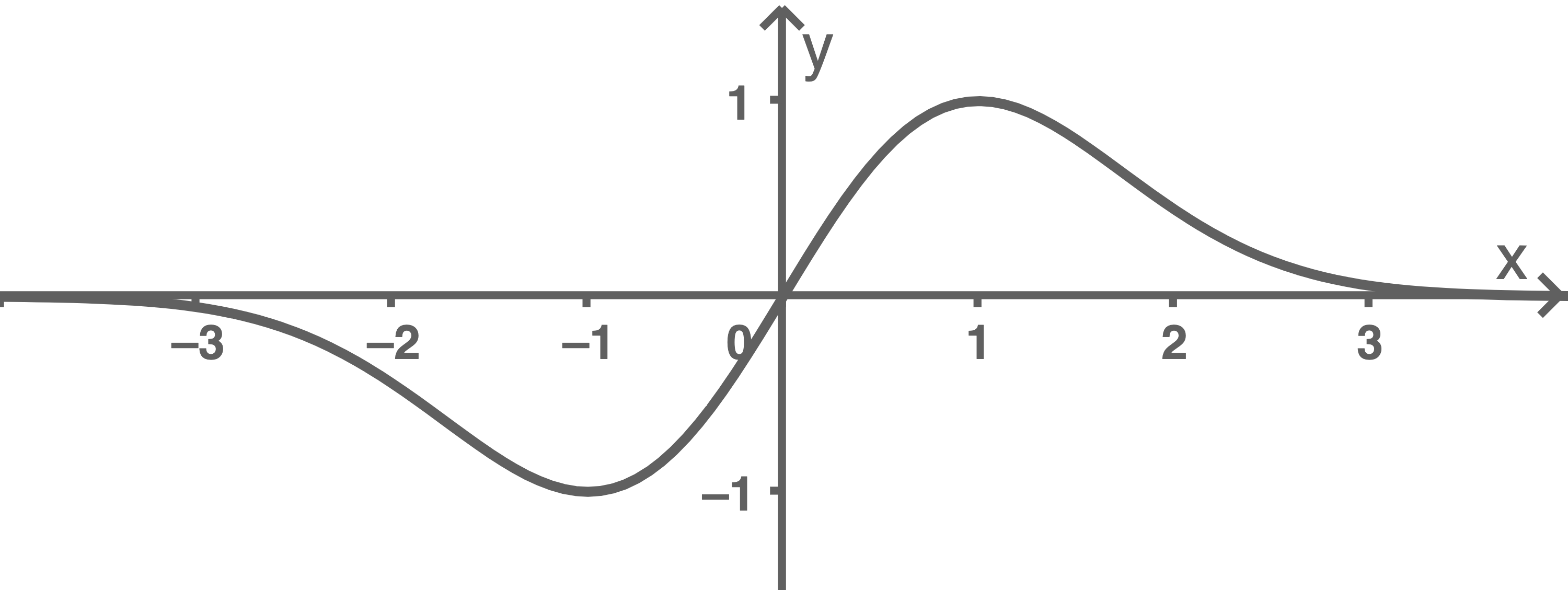
Die Abblidung 1 zeigt den Graphen von  ohne das zugrunde liegende Koordinatensystem. Ergänze die Koordinatenachsen und skaliere diese passend.
ohne das zugrunde liegende Koordinatensystem. Ergänze die Koordinatenachsen und skaliere diese passend.

(2 BE)

Abb. 1
c)
Interpretiere den folgenden Sachverhalt geometrisch:
-
Für jede Stammfunktion
(3 BE)
d)
Weise nach, dass der vertikale Abstand der Graphen von  und seiner ersten Ableitungsfunktion
und seiner ersten Ableitungsfunktion  ein relatives Maximum hat.
ein relatives Maximum hat.
Ermittle den Wert dieses Maximums.
Ermittle den Wert dieses Maximums.
(6 BE)
e)
Beschreibe die geometrische Bedeutung der Gleichung  .
.
(3 BE)
f)
Bestimme den Parameter  so, dass die Gleichung
so, dass die Gleichung  erfüllt ist.
erfüllt ist.
(1 BE)
g)
Der Graph von  ist eine Gerade. Gib die Steigung dieser Gerade und die Koordinaten ihres Schnittpunktes mit der
ist eine Gerade. Gib die Steigung dieser Gerade und die Koordinaten ihres Schnittpunktes mit der  -Achse an.
-Achse an.
(2 BE)
h)
Für einen Wert von  liegt der Punkt
liegt der Punkt  auf dem Graphen von
auf dem Graphen von  .
.
Berechne für diesen Wert von die Größe des Winkels, den der Graph von
die Größe des Winkels, den der Graph von  mit der Parallele zur
mit der Parallele zur  -Achse durch den Punkt
-Achse durch den Punkt  einschließt.
einschließt.
Berechne für diesen Wert von
(4 BE)
i)
Begründe unter Verwendung der Abbildung 2, dass
 gilt.
gilt.

Abb. 2
(2 BE)
2.
Nun werden alle Funktionen der gegebenen Schar betrachtet.
a)
Die folgenden Aussagen gelten für alle reellen Zahlen  und
und  :
:
oder
(3 BE)
b)
Zeige, dass die folgende Aussage für jeden Wert von  richtig ist:
richtig ist:
-
Wird der Graph von
(3 BE)
c)
Für  stimmen die Wendestellen von
stimmen die Wendestellen von  mit den Lösungen der Gleichung
mit den Lösungen der Gleichung  überein. Gib für alle Werte von
überein. Gib für alle Werte von  die Anzahl der Wendestellen von
die Anzahl der Wendestellen von  an und begründe deine Angabe.
an und begründe deine Angabe.
(5 BE)
d)
Beschreibe die Lage der Punkte  mit
mit  im Koordinatensystem und begründe, dass keiner dieser Punkte auf einem Graphen der Schar liegt. Zeige, dass jeder Punkt, der sowohl eine positive
im Koordinatensystem und begründe, dass keiner dieser Punkte auf einem Graphen der Schar liegt. Zeige, dass jeder Punkt, der sowohl eine positive  -Koordinate als auch eine positive
-Koordinate als auch eine positive  -Koordinate hat, auf genau einem Graphen der Schar liegt.
-Koordinate hat, auf genau einem Graphen der Schar liegt.
(5 BE)
e)
Alle Extrempunkte der Graphen der Schar liegen auf eine Gerade. Begründe, dass es sich dabei um die Gerade mit der Gleichung  handelt.
handelt.
(3 BE)
f)
Für jeden positiven Wert von  bilden der Hochpunkt
bilden der Hochpunkt  des Graphen von
des Graphen von  , der Punkt
, der Punkt  , der Koordinatenursprung und der Punkt
, der Koordinatenursprung und der Punkt  die Eckpunkte eines Vierecks. Bestimme ausgehend von einer geeigneten Skizze denjenigen Wert von
die Eckpunkte eines Vierecks. Bestimme ausgehend von einer geeigneten Skizze denjenigen Wert von  , für den das Viereck den Flächeninhalt
, für den das Viereck den Flächeninhalt  hat.
hat.
(5 BE)
(50 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Koordinaten des Hochpunkts angeben
 Der CAS liefert den Hochpunkt
Der CAS liefert den Hochpunkt  Nullstelle nachweisen
Nullstelle nachweisen
![\(\begin{array}[t]{rll}
f_1(x)&=& 0 \\[5pt]
x\cdot \mathrm e^{-\frac{1}{2}x^2+\frac{1}{2}}&=& 0
\end{array}\)](https://mathjax.schullv.de/1460d36eeec75253f6505d19f33b63b035832530f71d054f701955397ef9ca3f?color=5a5a5a) Mit dem Satz vom Nullprodukt folgt
Mit dem Satz vom Nullprodukt folgt  Da
Da  für alle
für alle  ist dies die einzige Nullstelle der Funktion.
Grenzwert angeben
ist dies die einzige Nullstelle der Funktion.
Grenzwert angeben

b)
c)
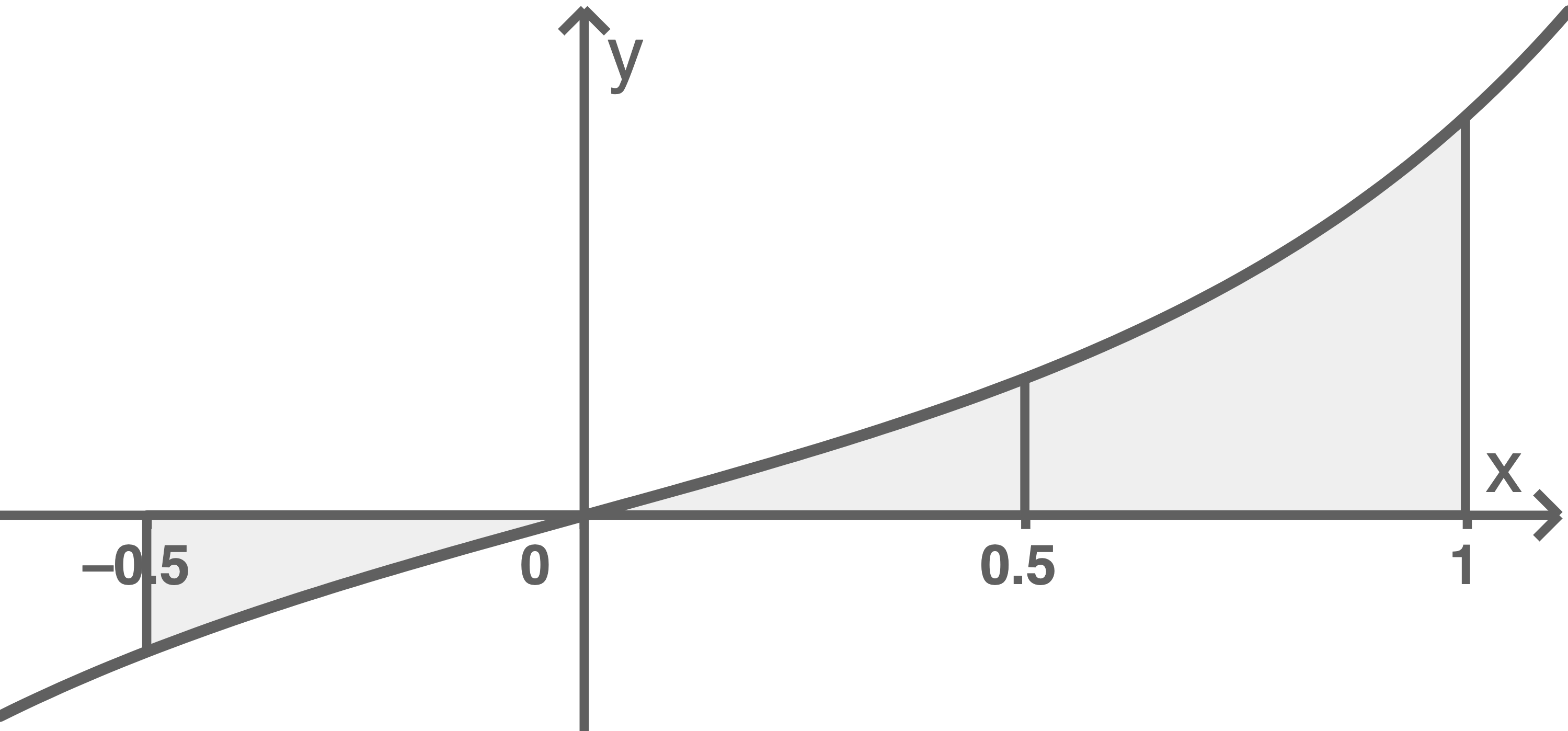
Für jede reelle Zahl  schließen der Graph von
schließen der Graph von  die
die  -Achse und die Gerade mit der Gleichung
-Achse und die Gerade mit der Gleichung  ein Flächenstück ein. Dessen Inhalt stimmt ungefähr mit dem Inhalt des Flächenstücks überein, das der Graph von
ein Flächenstück ein. Dessen Inhalt stimmt ungefähr mit dem Inhalt des Flächenstücks überein, das der Graph von  , die
, die  -Achse und die Gerade mit der Gleichung
-Achse und die Gerade mit der Gleichung  einschließen.
einschließen.
d)
e)
Die Tangente an den Graphen von  an der Stelle
an der Stelle  steht senkrecht zur Tangente des Graphen von
steht senkrecht zur Tangente des Graphen von  an der Stelle
an der Stelle 
f)
Der solve-Befehl des CAS liefert 
g)
h)
1. Schritt: Wert von  berechnen
berechnen
![\(\begin{array}[t]{rll}
f_a(1)&=& \mathrm e \\[5pt]
\mathrm e^{-\frac{1}{2}a+\frac{1}{2}}&=& \mathrm e \\[5pt]
\end{array}\)](https://mathjax.schullv.de/fde859e6c48421087effd50319754392e6b942787bf16cb4b3daa3d9ce60602d?color=5a5a5a) Der solve-Befehl des CAS liefert
Der solve-Befehl des CAS liefert  2. Schritt: Winkel berechnen
Der gesuchte Winkel lässt sich wie folgt berechnen:
2. Schritt: Winkel berechnen
Der gesuchte Winkel lässt sich wie folgt berechnen:
![\(\begin{array}[t]{rll}
\tan(\alpha)&=& f](https://mathjax.schullv.de/64450528e044aa1294b79812b87da6bd5297123336816ce4ad4b41d1dcbaaf19?color=5a5a5a) Der gesuchte Winkel beträgt ca.
Der gesuchte Winkel beträgt ca. 
i)
Die Flächen, die der Graph von  mit der
mit der  -Achse im Intervall
-Achse im Intervall ![\([-0,5;0]\)](https://mathjax.schullv.de/b2dc1dcef21ead820d4f5b6a0016d623e6405094c033f4866216bff2d67d55fd?color=5a5a5a) und
und ![\([0;0,5]\)](https://mathjax.schullv.de/8df4e9b70d9d2b061d26258c569e309a1f04326120674d13823b56dc3ea5e974?color=5a5a5a) einschließt, sind gleich groß. Da die eine Fläche oberhalb und die andere unterhalb der
einschließt, sind gleich groß. Da die eine Fläche oberhalb und die andere unterhalb der  -Achse liegt, hat das Intregral über das Intervall
-Achse liegt, hat das Intregral über das Intervall ![\([-0,5;0,5]\)](https://mathjax.schullv.de/6f30891beb1beb6a7a765054330e09bcba3bbfe8432be6aaec519a1e3b97d256?color=5a5a5a) den Wert Null.
den Wert Null.
2
a)
Aus der ersten Aussage folgt, dass alle Funktionen der Schar für jedes  durch den Koordinatenursprung verlaufen.
Aus der zweiten Aussage folgt weiter, dass die Funktionen im Koordinatenursprung außerdem die gleiche Steigung haben.
Aus der dritten Aussage folgt, dass die Graphen der Funktionenschar für unterschiedliche
durch den Koordinatenursprung verlaufen.
Aus der zweiten Aussage folgt weiter, dass die Funktionen im Koordinatenursprung außerdem die gleiche Steigung haben.
Aus der dritten Aussage folgt, dass die Graphen der Funktionenschar für unterschiedliche  keinen weiteren gemeinsamen Punkt haben.
keinen weiteren gemeinsamen Punkt haben.
b)
Streckt man den Graphen von  mit dem Faktor
mit dem Faktor  in
in  - und
- und  -Richtung, so ergibt sich die folgende Funktion:
-Richtung, so ergibt sich die folgende Funktion:
![\(\begin{array}[t]{rll}
k\cdot f_a\left(\dfrac{x}{k}\right)&=& k\cdot \dfrac{x}{k}\cdot \mathrm e^{-\frac{1}{2}a\cdot\left(\frac{x}{k}\right)^2+\frac{1}{2}} \\[5pt]
&=& x\cdot \mathrm e^{-\frac{1}{2}\cdot\frac{a}{k^2}\cdot x^2+\frac{1}{2}} \\[5pt]
&=& f_{\frac{a}{k^2}}(x)
\end{array}\)](https://mathjax.schullv.de/50a755b91d71ab0e53bb6273ce3e5618f4d80e1e4fa4860d2ffe800f720f8f36?color=5a5a5a) Es handelt sich also wieder um eine Funktion der Schar mit dem Parameter
Es handelt sich also wieder um eine Funktion der Schar mit dem Parameter 
c)
Für  gilt
gilt  Die Funktion ist also eine Gerade und hat somit keinen Wendepunkt.
Für
Die Funktion ist also eine Gerade und hat somit keinen Wendepunkt.
Für  sind die Wendestellen durch die Nullstellen der Gleichung
sind die Wendestellen durch die Nullstellen der Gleichung  gegeben. Nach dem Satz vom Nullprodukt hat die Gleichung die Lösung
gegeben. Nach dem Satz vom Nullprodukt hat die Gleichung die Lösung  sowie:
sowie:
![\(\begin{array}[t]{rll}
a\cdot x^2-3&=& 0 \quad \scriptsize \mid\;+3 \\[5pt]
a\cdot x^2&=& 3 \quad \scriptsize \mid\;:a \\[5pt]
x^2&=& \dfrac{3}{a}
\end{array}\)](https://mathjax.schullv.de/0d66203bbce8d4a50000d599714bc493d454a4e7fb63bd11e8afe77b68fc46c9?color=5a5a5a) Für
Für  hat die Gleichung nur die Lösung
hat die Gleichung nur die Lösung  Damit hat
Damit hat  genau eine Wendestelle.
Für
genau eine Wendestelle.
Für  hat die Gleichung die Lösungen
hat die Gleichung die Lösungen 
 und
und  also hat
also hat  genau drei Wendestellen.
genau drei Wendestellen.
d)
Lage der Punkte beschreiben
Alle Punkte  mit
mit  liegen im zweiten oder vierten Quadranten.
Begründen, dass keiner der Punkte auf einem Graphen der Schar liegt
Es gilt
liegen im zweiten oder vierten Quadranten.
Begründen, dass keiner der Punkte auf einem Graphen der Schar liegt
Es gilt  für alle
für alle  Damit folgt
Damit folgt  für
für  und
und  für
für  Also gilt
Also gilt  für alle Punkte, die auf einem Graphen der Schar liegen.
Zeigen, dass Punkte auf genau einem Graphen der Schar liegen
Zu jedem Punkt mit positiver
für alle Punkte, die auf einem Graphen der Schar liegen.
Zeigen, dass Punkte auf genau einem Graphen der Schar liegen
Zu jedem Punkt mit positiver  - und
- und  -Koordinate existiert also genau ein zugehöriger Graph der Schar.
-Koordinate existiert also genau ein zugehöriger Graph der Schar.
e)
f)
Für den Flächeninhalt  gilt:
gilt:
![\(\begin{array}[t]{rll}
A&=& 144 \\[5pt]
v^2 + \dfrac{1}{2} (2-v) \cdot v &=& 144 \\[5pt]
v^2 + v - \dfrac{1}{2} \cdot v^2 &=& 144 \\[5pt]
\dfrac{1}{2} \cdot v^2 + v &=& 144 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/d3988f98ea02a2afb20323b0a11cf3c321e41e2e6f5f95fb468185b4b0e96967?color=5a5a5a) Der solve-Befehl des CAS liefert
Der solve-Befehl des CAS liefert 
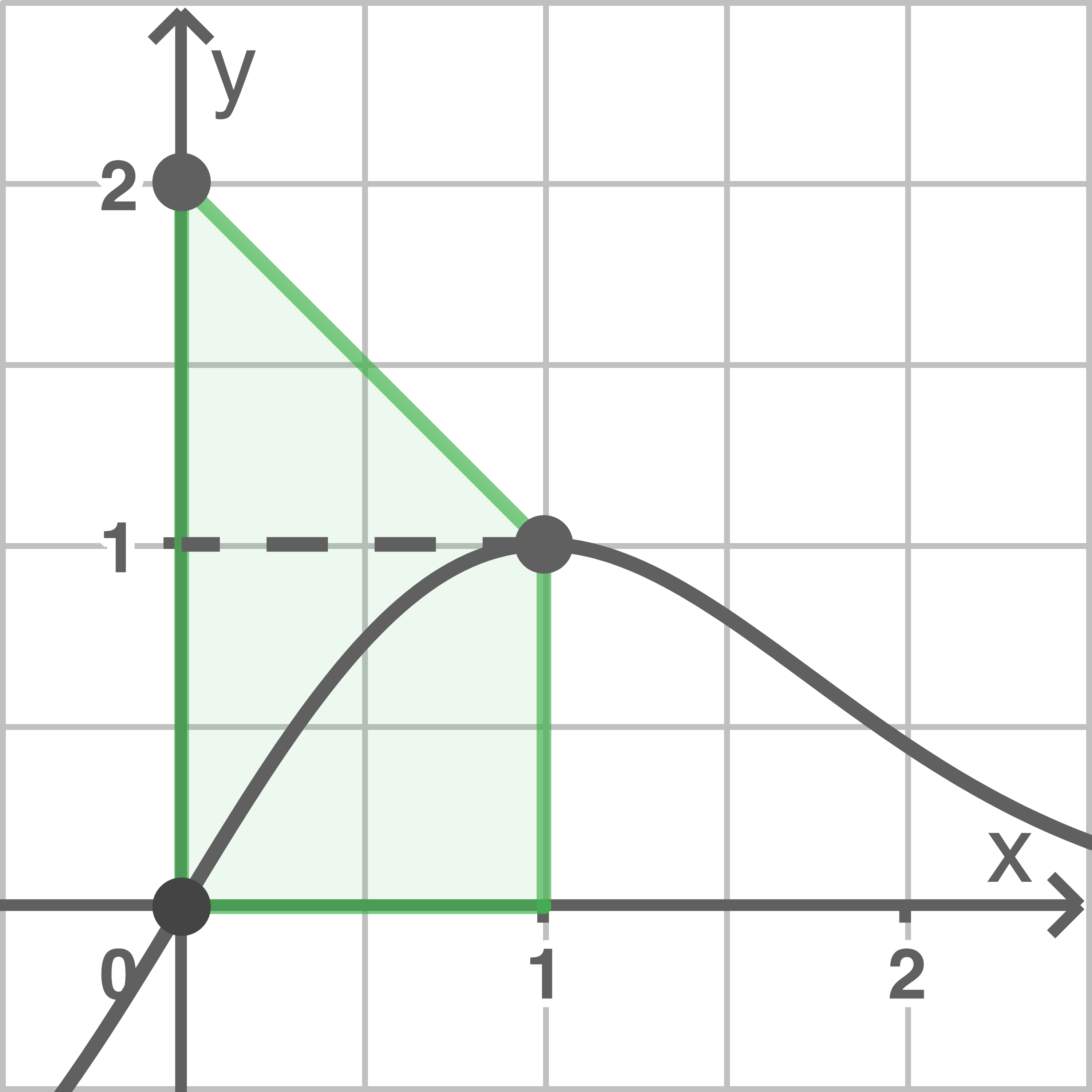
Skizze für  und
und 