Stochastik 3 - Urlaubsreise
1
Für ein Land wird die Gruppe derjenigen Personen betrachtet, die im Jahr 2022 eine Urlaubsreise unternahmen.  dieser Personen sind weiblich. Der Anteil derjenigen, die mit ihrer Urlaubsreise zufrieden waren, beträgt unter den weiblichen Personen
dieser Personen sind weiblich. Der Anteil derjenigen, die mit ihrer Urlaubsreise zufrieden waren, beträgt unter den weiblichen Personen  ; der entsprechende Anteil unter den nicht weiblichen Personen wird mit
; der entsprechende Anteil unter den nicht weiblichen Personen wird mit  bezeichnet.
bezeichnet.


a)
Für eine Umfrage werden 200 Personen aus der betrachteten Gruppe zufällig ausgewählt. Berechnne die Wahrscheinlichkeit folgender Ereignisse:


Aus der Gruppe der Personen, die im Jahr 2022 eine Urlaubsreise unternahmen, wird eine Person zufällig ausgewählt. Untersucht werden die folgenden Ereignisse:
„Mehr als die Hälfte der ausgewählten Personen sind weiblich.“
„Höchstens  der ausgewählten Personen sind weiblich.“
der ausgewählten Personen sind weiblich.“
(4 BE)
„Die Person ist weiblich.“
„Die Person war mit ihrer Urlaubsreise zufrieden.“
b)
Interpretiere den Term 


 im Sachzusammenhang.
im Sachzusammenhang.
(2 BE)
c)
Stelle den Sachzusammenhang zu den Ereignissen  und
und  in einem beschrifteten Baumdiagramm dar. Bestimme denjenigen Wert von
in einem beschrifteten Baumdiagramm dar. Bestimme denjenigen Wert von  für den die Wahrscheinlichkeit dafür, dass die ausgewählte Person mit ihrer Urlaubsreise zufrieden war,
für den die Wahrscheinlichkeit dafür, dass die ausgewählte Person mit ihrer Urlaubsreise zufrieden war,  beträgt.
beträgt.
(4 BE)
d)
Weise nach, dass es in der betrachteten Gruppe für  weniger weibliche als nicht weibliche Personen geben würde, die mit ihrer Urlaubsreise zufrieden waren.
weniger weibliche als nicht weibliche Personen geben würde, die mit ihrer Urlaubsreise zufrieden waren.
(2 BE)
e)
Gib denjenigen Wert von  an, für den
an, für den  und
und  stochastisch unabhängig wären, und begründe deine Angabe, ohne zu rechnen.
stochastisch unabhängig wären, und begründe deine Angabe, ohne zu rechnen.
(3 BE)
f)
Eine ausgewählte Person war mit ihrer Urlaubsreise nicht zufrieden.
Begründe im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass die Person weiblich ist, mit zunehmendem Wert von zunimmt.
zunimmt.
Begründe im Sachzusammenhang, dass die Wahrscheinlichkeit dafür, dass die Person weiblich ist, mit zunehmendem Wert von
(3 BE)
2
Ein großes Reiseunternehmen führt auf seinen Internetseiten ein kostenloses Gewinnspiel durch. Jede Person kann nur einmal an dem Spiel teilnehmen. Als Ergebnis des Spiels wird eine bestimmte Anzahl von Strandkörben angezeigt; diese Anzahl beträgt mindestens 1 und höchstens 5. Im Folgenden sind dazu die möglichen Gewinne beschrieben:
 Cent.
Cent.
 bezeichnet. Für das Unternehmen wäre eine Verlängerung des Gewinnspiels für
bezeichnet. Für das Unternehmen wäre eine Verlängerung des Gewinnspiels für  mit Vorteilen verbunden, für
mit Vorteilen verbunden, für  dagegen mit finanziellen Verlusten. Die Nullhypothese „
dagegen mit finanziellen Verlusten. Die Nullhypothese „ beträgt mindestens
beträgt mindestens  .“ soll auf einem Signifikanzniveau von
.“ soll auf einem Signifikanzniveau von  getestet werden.
getestet werden.
 Personen online eine Reise.
Personen online eine Reise.  Personen davon sind weiblich.
Personen davon sind weiblich.  Personen werden zufällig für ein Gewinnspiel ausgewählt.
Personen werden zufällig für ein Gewinnspiel ausgewählt.
- Unter den teilnehmenden Personen, bei denen nur ein Strandkorb angezeigt wird, werden Sachgewinne verlost.
- Die teilnehmenden Personen mit zwei, drei, vier oder fünf Strandkörben erhalten jeweils einen Reisegutschein. Der folgenden Tabelle können die Werte der Gutscheine sowie die Wahrscheinlichkeiten für diese Gewinne entnommen werden.
a)
Zeige, dass die Wahrscheinlichkeit dafür, dass bei dem Spiel nur ein Strandkorb angezeigt wird, um weniger als ein Tausendstel von  abweicht. Bestimme für die Personen mit einem Strandkorb den Erwartungswert des Gewinns pro Person.
abweicht. Bestimme für die Personen mit einem Strandkorb den Erwartungswert des Gewinns pro Person.
(4 BE)
b)
Es soll davon ausgegangen werden, dass  Personen an dem Spiel teilnehmen werden. Der Erwartungswert der Anzahl der Personen mit zwei Strandkörben wird mit
Personen an dem Spiel teilnehmen werden. Der Erwartungswert der Anzahl der Personen mit zwei Strandkörben wird mit  bezeichnet. Ermittle den kleinsten möglichen ganzzahligen Wert von
bezeichnet. Ermittle den kleinsten möglichen ganzzahligen Wert von  für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens
für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens  im Intervall
im Intervall ![\([\mu-c ; \mu+c]\)](https://mathjax.schullv.de/abede9fd9d6983456aa27d37774c63086a41d2df2e0b6d5b802f80d190c19e7a?color=5a5a5a) liegt.
liegt.
Die Wahrscheinlichkeit dafür, dass eine zufällig ausgewählte Person nach der Teilnahme am Gewinnspiel eine Reise bei dem Reiseunternehmen bucht, wird mit
(4 BE)
c)
Bestimme die zugehörige Entscheidungsregel für einen Stichprobenumtang von  Personen.
Personen.
(4 BE)
d)
Bei einer Wiederholung der Befragung mit einem Stichprobenumfang von  wird die Nullhypothese abgelehnt, wenn weniger als 11 Personen eine Reise buchen.
wird die Nullhypothese abgelehnt, wenn weniger als 11 Personen eine Reise buchen.
Ermittele bei dieser Befragung für zwei geeignete Werte von den Fehler 2. Art und interpretiere diesen im Sachzusammenhang.
den Fehler 2. Art und interpretiere diesen im Sachzusammenhang.
An einem bestimmten Tag buchen Ermittele bei dieser Befragung für zwei geeignete Werte von
(4 BE)
e)
Ermittle die Wahrscheinlichkeit dafür, dass davon alle Personen weiblich sind.
(2 BE)
f)
Die Wahrscheinlichkeit, dass unter den  ausgewählten Personen höchstens
ausgewählten Personen höchstens  Personen weiblich sind, soll kleiner als
Personen weiblich sind, soll kleiner als  sein.
sein.
Ermittle das größtmögliche
Ermittle das größtmögliche
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
b)
Der Term gibt die Wahrscheinlichkeit dafür an, dass die Person entweder weiblich ist oder mit der Reise zufrieden war.
c)
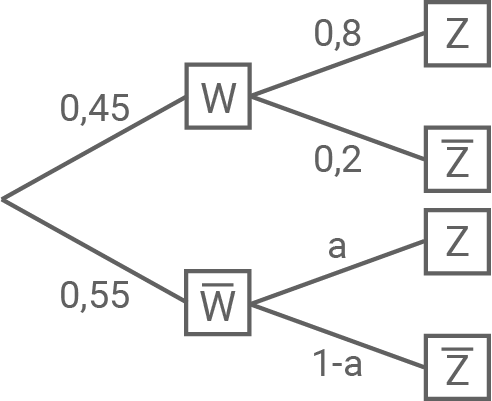
d)
e)
Für  ist der Anteil derjenigen, die mit ihrer Urlaubsreise zufrieden waren, unter den nicht weiblichen Personen ebenso groß wie unter den weiblichen. Für diesen Wert von
ist der Anteil derjenigen, die mit ihrer Urlaubsreise zufrieden waren, unter den nicht weiblichen Personen ebenso groß wie unter den weiblichen. Für diesen Wert von  sind
sind  und
und  somit stochastisch unabhängig.
somit stochastisch unabhängig.
f)
Mit zunehmendem Wert von  nimmt der Anteil derjenigen, die mit ihrer Urlaubsreise nicht zufrieden waren, unter den nicht weiblichen Personen ab, während er unter den weiblichen Personen konstant bleibt. Damit nimmt unter den Personen, die mit ihrer Urlaubsreise nicht zufrieden waren, der Anteil der weiblichen Personen zu.
nimmt der Anteil derjenigen, die mit ihrer Urlaubsreise nicht zufrieden waren, unter den nicht weiblichen Personen ab, während er unter den weiblichen Personen konstant bleibt. Damit nimmt unter den Personen, die mit ihrer Urlaubsreise nicht zufrieden waren, der Anteil der weiblichen Personen zu.
2
a)
Wahrscheinlichkeit für einen Strandkorb berechnen
 Nur ein Strandkorb wird angezeigt
Nur ein Strandkorb wird angezeigt





 Da
Da 

 gilt, weicht die Wahrscheinlichkeit um weniger als ein Tausendstel von
gilt, weicht die Wahrscheinlichkeit um weniger als ein Tausendstel von  ab.
Erwartungswert des Gewinns bestimmen
ab.
Erwartungswert des Gewinns bestimmen





![\( =0,435\;[€]\)](https://mathjax.schullv.de/18d27ef0afdce1f6f57c64839cb2413e5994b4015c3212c60394807a5d05ad1e?color=5a5a5a) Mit dem solve-Befehl des CAS folgt:
Mit dem solve-Befehl des CAS folgt:

b)
Wert von  bestimmen
bestimmen



 Wert von
Wert von  ermitteln
Systematisches Ausprobieren liefert:
ermitteln
Systematisches Ausprobieren liefert:



 Der kleinstmögliche Wert für
Der kleinstmögliche Wert für  , für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens
, für den die Anzahl der Personen mit zwei Strandkörben mit einer Wahrscheinlichkeit von mindestens  im Intervall
im Intervall ![\([\mu-c ; \mu+c]\)](https://mathjax.schullv.de/abede9fd9d6983456aa27d37774c63086a41d2df2e0b6d5b802f80d190c19e7a?color=5a5a5a) liegt, beträgt somit
liegt, beträgt somit 
c)
d)
1. Schritt: Fehler 2. Art ermitteln
Zu betrachten sind die Fälle, in denen  gilt, aber die Nullhypothese nicht abgelehnt wird. Zwei geeignete Werte sind somit
gilt, aber die Nullhypothese nicht abgelehnt wird. Zwei geeignete Werte sind somit  und
und 





 2. Schritt: Ergebnisse im Sachzusammenhang interpretieren
Wenn der tatsächliche Wert von
2. Schritt: Ergebnisse im Sachzusammenhang interpretieren
Wenn der tatsächliche Wert von  nur leicht unterhalb von
nur leicht unterhalb von  liegt, ist die Wahrscheinlichkeit groß, die Nullhypothese nicht abzulehnen, obwohl sie nicht zutreffend ist.
liegt, ist die Wahrscheinlichkeit groß, die Nullhypothese nicht abzulehnen, obwohl sie nicht zutreffend ist.
e)
f)
Mit der Zufallsvariable  aus Aufgabenteil e) soll gelten:
aus Aufgabenteil e) soll gelten:





 Eingabe in den CAS liefert:
Eingabe in den CAS liefert:





 Da
Da 

 gilt, muss
gilt, muss  kleiner als 2 sein. Es folgt:
kleiner als 2 sein. Es folgt:


 Das größtmögliche
Das größtmögliche  ist damit durch
ist damit durch  gegeben.
gegeben.