Analytische Geometrie 3.1 - Doppelpyramide
Analytische Geometrie: Doppelpyramide
Gegeben sind die Punkte
a)
Zeige, dass das Dreieck  gleichschenklig ist.
gleichschenklig ist.
(2 BE)
b)
Begründe, dass 
 und
und  Eckpunkte eines Quadrats sein können, und gib die Koordinaten des vierten Eckpunkts
Eckpunkte eines Quadrats sein können, und gib die Koordinaten des vierten Eckpunkts  dieses Quadrats an.
dieses Quadrats an.
(3 BE)
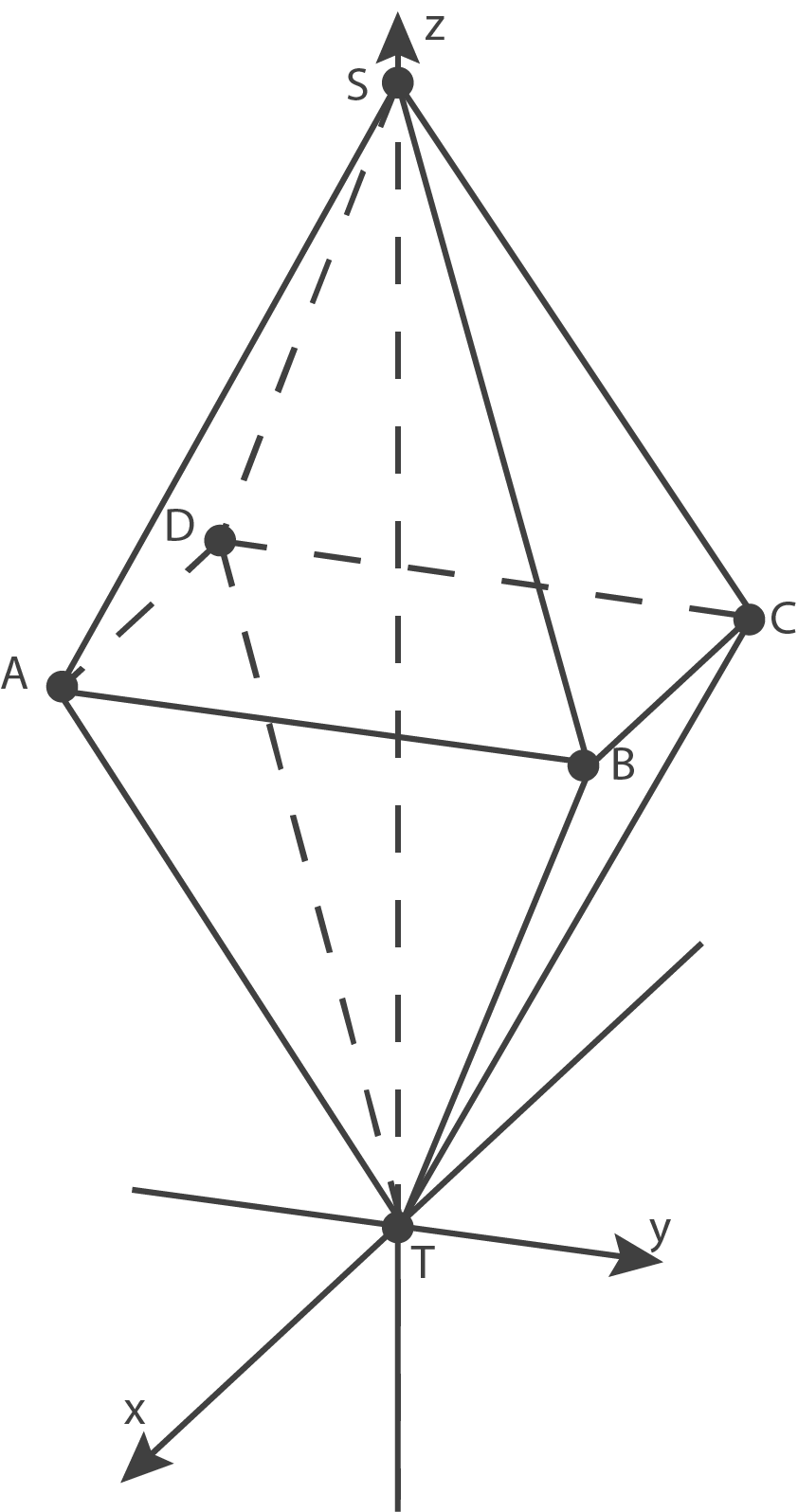
Im Folgenden wird die abgebildete Doppelpyramide betrachtet. Die beiden Teilpyramiden  und
und  sind gleich hoch.
sind gleich hoch.
Der Punkt liegt im Koordinatenursprung, der Punkt
liegt im Koordinatenursprung, der Punkt  ebenfalls auf der
ebenfalls auf der  -Achse.
-Achse.
Die Seitenfläche liegt in einer Ebene
liegt in einer Ebene 
Der Punkt
Die Seitenfläche
c)
Die Doppelpyramide hat 12 Kanten. Jede Kante liegt auf einer Geraden, die durch zwei Eckpunkte der Doppelpyramide festgelegt ist. Die Kante  der Doppelpyramide liegt auf der Geraden
der Doppelpyramide liegt auf der Geraden 
Gib jeweils zwei Eckpunkte an, durch die eine Gerade und eine Gerade
und eine Gerade  verlaufen, für die gilt:
verlaufen, für die gilt:
Gib jeweils zwei Eckpunkte an, durch die eine Gerade
und
sind windschief
und
sind echt parallel
(2 BE)
d)
Ermittle den Flächeninhalt des Dreiecks 
(3 BE)
e)
Bestimme eine Gleichung von  in Koordinatenform.
(zur Kontrolle:
in Koordinatenform.
(zur Kontrolle:  )
)
(3 BE)
f)
Bestimme die Größe des Winkels, den die Seitenfläche  mit der Fläche
mit der Fläche  einschließt.
einschließt.
Die Ebene
(3 BE)
g)
Alle Ebenen der Schar schneiden sich in einer Gerade. Weise nach, dass die Kante  auf dieser Geraden liegt.
auf dieser Geraden liegt.
(2 BE)
h)
Ermittle diejenigen Werte von  für die
für die  mit der Seitenfläche
mit der Seitenfläche  mindestens einen Punkt gemeinsam hat.
mindestens einen Punkt gemeinsam hat.
(4 BE)
i)
Die Seitenfläche  liegt in der Ebene
liegt in der Ebene  Gib einen Normalenvektor von
Gib einen Normalenvektor von  an und begründe deine Angabe, ohne die Koordinaten von
an und begründe deine Angabe, ohne die Koordinaten von  und
und  zu verwenden.
zu verwenden.
Bestimme denjenigen Wert von für den
für den  senkrecht zu
senkrecht zu  steht.
steht.
Bestimme denjenigen Wert von
(4 BE)
j)
Die Doppelpyramide wird so um die  -Achse gedreht, dass die bisher mit
-Achse gedreht, dass die bisher mit  bezeichnete Seitenfläche in der
bezeichnete Seitenfläche in der  -Ebene liegt und der bisher mit
-Ebene liegt und der bisher mit  bezeichnete Punkt eine positive
bezeichnete Punkt eine positive  -Koordinate hat.
-Koordinate hat.
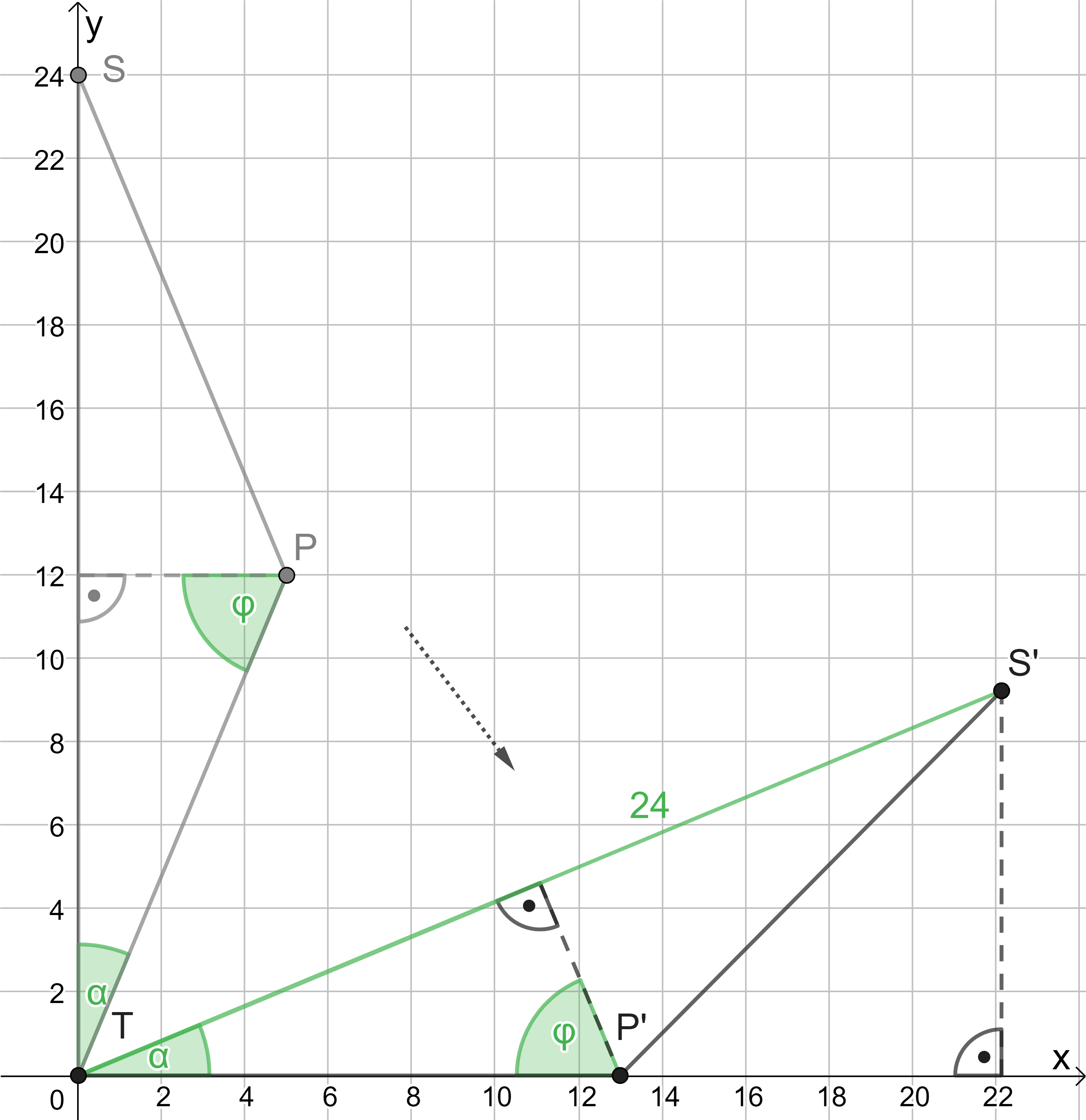
Bestimme diese -Koordinate und veranschauliche dein Vorgehen durch eine Skizze.
-Koordinate und veranschauliche dein Vorgehen durch eine Skizze.
Bestimme diese
(4 BE)
k)
Die Ebene  mit
mit  teilt die Doppelpyramide in zwei Teilkörper.
teilt die Doppelpyramide in zwei Teilkörper.
Ermittle die Volumina der beiden Teilkörper.
Ermittle die Volumina der beiden Teilkörper.
(5 BE)
l)
Die Doppelpyramide wird durch eine Ebene  geschnitten. Die Schnittfläche der Ebene
geschnitten. Die Schnittfläche der Ebene  mit der Doppelpyramide ist ein Drachenviereck. Der Schnittpunkt der Diagonalen dieses Drachenvierecks ist der Punkt
mit der Doppelpyramide ist ein Drachenviereck. Der Schnittpunkt der Diagonalen dieses Drachenvierecks ist der Punkt  Ein Eckpunkt dieses Drachenvierecks ist der Punkt
Ein Eckpunkt dieses Drachenvierecks ist der Punkt 
Ermittle die Koordinaten der anderen drei Eckpunkte des Drachenvierecks.
Ermittle die Koordinaten der anderen drei Eckpunkte des Drachenvierecks.
(5 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Ein Dreieck ist gleichschenklig, wenn mindestens zwei Seiten die gleiche Länge haben.

 Somit ist das Dreieck gleichschenklig.
Somit ist das Dreieck gleichschenklig.
b)
Damit die drei Punkte den Eckpunkten eines Quadrats entsprechen, muss das Dreieck  einen rechten Winkel haben. Das Skalarprodukt von zwei Richtungsvektoren muss also null sein.
einen rechten Winkel haben. Das Skalarprodukt von zwei Richtungsvektoren muss also null sein.
 Nun wird der Punkt
Nun wird der Punkt  ermittelt. Es gilt:
ermittelt. Es gilt:



c)
Zwei Geraden sind windschief zueinander, wenn sie sich in einem Punkt schneiden.  und
und  sind windschief, wenn
sind windschief, wenn  durch die Punkte
durch die Punkte  und
und  verlaufen.
verlaufen.
 und
und  verlaufen paralell zueinander, wenn
verlaufen paralell zueinander, wenn  durch die Punkte
durch die Punkte  und
und  verläuft.
verläuft.
d)
Zunächst wird der Mittelpunkt  der Strecke
der Strecke  bestimmt:
bestimmt:
 Nun wird die Länge der Strecken
Nun wird die Länge der Strecken  und
und  berechnet:
berechnet:





e)
Die Punkte  ,
,  und
und  liegen in der Ebenen
liegen in der Ebenen  . Als Stützpunkt kann der Punkt
. Als Stützpunkt kann der Punkt  verwendet werden. Als Spannvektoren werden
verwendet werden. Als Spannvektoren werden  und
und  gewählt.
gewählt.

 Es ergibt sich:
Es ergibt sich:


 Nun wird das Kreuzprodukt der beiden Spannvektoren berechnet. Es gibt den Normalenvektor
Nun wird das Kreuzprodukt der beiden Spannvektoren berechnet. Es gibt den Normalenvektor  an.
an.
 Somit lautet die Koordinatenform:
Somit lautet die Koordinatenform:

f)
g)
Wenn die Punkte  und
und  in der Ebenenschar
in der Ebenenschar  liegen, liegt die gesamte Gerade
liegen, liegt die gesamte Gerade  ebenfalls in
ebenfalls in  Die beiden Punkte werden also in die Ebenengleichung eingesetzt.
Die beiden Punkte werden also in die Ebenengleichung eingesetzt.

 Somit liegt
Somit liegt  in
in 
h)
Zunächst wird der allgemeine Schnittpunkt  von der Ebenenschar und der
von der Ebenenschar und der  -Achse bestimmt:
-Achse bestimmt:


 Damit es mindestens einen Schnittpunkt zwischen
Damit es mindestens einen Schnittpunkt zwischen  und
und  gibt, müssen die
gibt, müssen die  -Koordinaten des Schnittpunkts mindestens 12 und höchstens 24 betragen. Für
-Koordinaten des Schnittpunkts mindestens 12 und höchstens 24 betragen. Für  gilt somit:
gilt somit:

i)
Der Normalenvektor  der Ebenen
der Ebenen  entspricht dem Normalenvektor der Ebenen
entspricht dem Normalenvektor der Ebenen  an der
an der  -Ebene gespiegelt.
-Ebene gespiegelt.
 Zwei Ebenen stehen senkrecht aufeinander, wenn das Skalarprodukt ihrer Normalenvektoren null ergibt.
Zwei Ebenen stehen senkrecht aufeinander, wenn das Skalarprodukt ihrer Normalenvektoren null ergibt.




j)
Der Winkel  liegt zwischen der Ebene
liegt zwischen der Ebene  und der
und der  -Ebene. Somit ergibt sich für den Kosinus:
-Ebene. Somit ergibt sich für den Kosinus:

 kann aus mit Hilfe von
kann aus mit Hilfe von  aus Teilaufgabe f) bestimmt werden:
aus Teilaufgabe f) bestimmt werden:
 Somit gilt:
Somit gilt:


k)
Der erste Teilkörper  ist eine kleine Pyramide. Der zweite Teilkörper ist ein eine abgeschnittene Doppelpyramide. Zunächst wird das Volumen der kleinen Pyramide berechnet.
Berechnung der Koordinaten der Schnittpunkte
ist eine kleine Pyramide. Der zweite Teilkörper ist ein eine abgeschnittene Doppelpyramide. Zunächst wird das Volumen der kleinen Pyramide berechnet.
Berechnung der Koordinaten der Schnittpunkte  und
und 
 In
In  einsetzten:
einsetzten:
 Für
Für  ergibt sich also:
ergibt sich also:

 aus
aus  ergibt sich:
ergibt sich:
 Nun kann die Seitenlänge
Nun kann die Seitenlänge  bestimmt werden:
bestimmt werden:
 Daraus lässt sich das Volumen der Pyramide
Daraus lässt sich das Volumen der Pyramide  berechnen:
berechnen:

 Für das Volumen der größeren Pyramide
Für das Volumen der größeren Pyramide  gilt:
gilt:
 Für das Volumen des zweiten Teilkörpers gilt:
Für das Volumen des zweiten Teilkörpers gilt:


l)
Einer der Eckpunkte entspricht dem Schnittpunkt der beiden Geraden  und
und 





 kann nun in
kann nun in  Für den zweiten Eckpunkt ergibt sich somit:
Für den zweiten Eckpunkt ergibt sich somit:
 Durch den Punkt
Durch den Punkt  und parallel zur Diagonalen
und parallel zur Diagonalen  wird nun die Gerade
wird nun die Gerade  erstellt:
erstellt:
 Der Eckpunkt
Der Eckpunkt  entspricht dem Schnittpunkt von
entspricht dem Schnittpunkt von  und
und 



 Einsetzten in
Einsetzten in 
 Der Eckpunkt
Der Eckpunkt  entspricht dem Schnittpunkt von
entspricht dem Schnittpunkt von  und
und 



 Einsetzten in
Einsetzten in