Analysis 2.1 - Funktionenschar

Gegeben ist die in $\mathbb R$ definierte Funktion $f_a$ mit $f_a(x)=\dfrac{1}{8}x^4-\dfrac{a}{12}x^3+2x; a \in \mathbb R$ .
Der Graph wird mit $G_a$ bezeichnet.
Für die erste Ableitungsfunktion von $f_a$ gilt $\(f$ .

Gib das Verhalten der Funktionswerte von $f_a$ für $x\rightarrow +\infty$ und für $x\rightarrow -\infty$ an.

(2 BE)

Weise nach, dass $G_0$ genau einen lokalen Tiefpunkt besitzt und bestimme dessen Koordinaten.

(3 BE)

Ermittle eine Gleichung der Tangente $t_0$ an den Graphen $G_0$ im Schnittpunkt mit der $y$ -Achse. Begründe, dass $t_0$ Tangente aller Graphen $G_a$ im Schnittpunkt mit der $y$ -Achse ist.

$\bigg($ Zur Kontrolle: $y=2x$ $\bigg)$

(4 BE)

An den Graphen $G_a$ für $a\neq0$ wird im Punkt $B\left(x\mid f_a(x)\right); x\neq0$ eine Tangente gelegt, die parallel zur Tangente $t_0$ aus Teilaufgabe c verläuft.
Ermittle einen Wert des Parameters $a$ , für den der Abstand der beiden Tangenten $1920\cdot \sqrt{5}\,\text{LE}$ beträgt.

(6 BE)

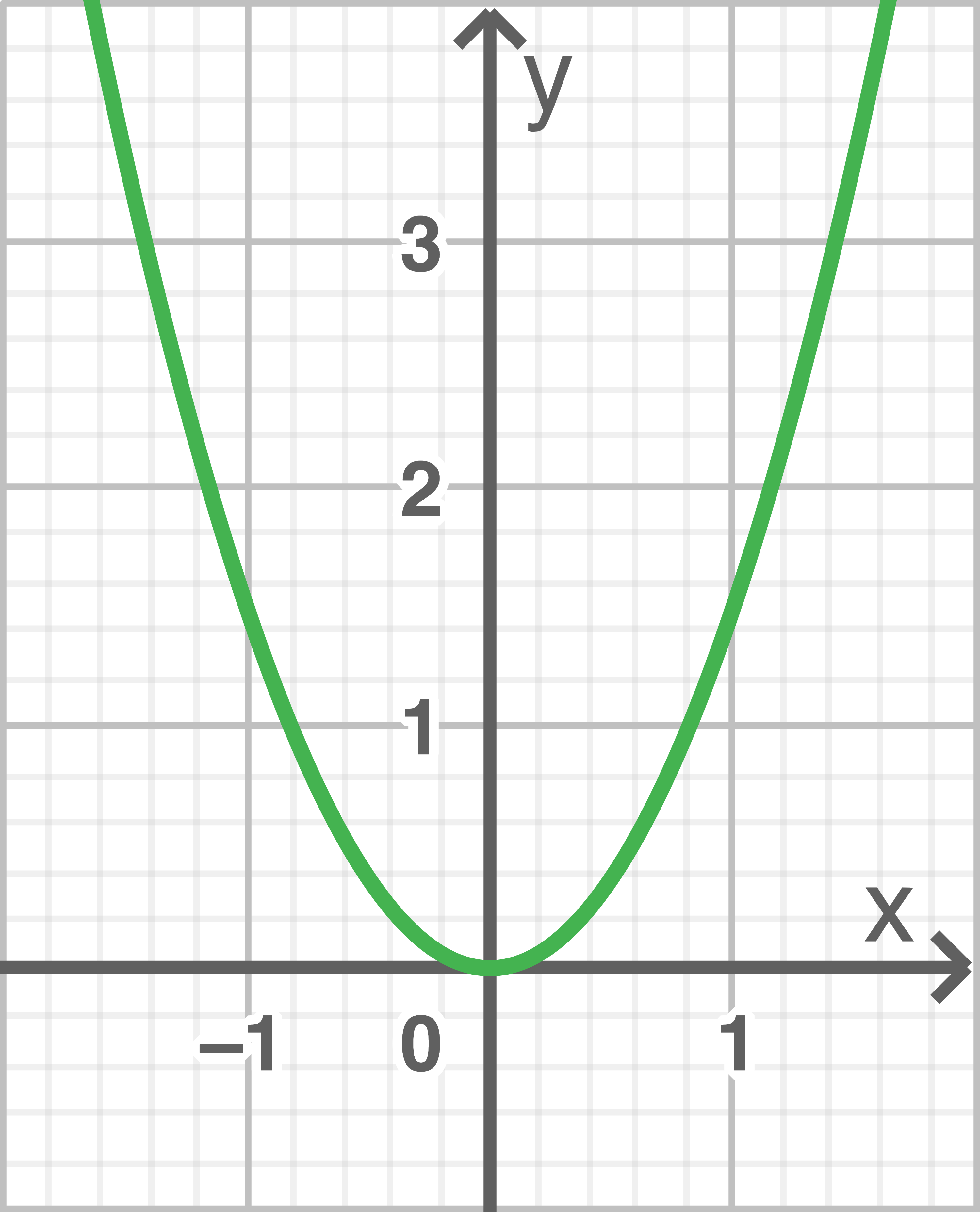
Die Abbildung 1 zeigt den Graphen der zweiten Ableitungsfunktion der Funktion $f_0.$
Begründe mithilfe dieses Graphen, dass der Punkt $\left(0\mid f_0(0) \right)$ kein Wendepunkt des Graphen $G_0$ ist.

berlin mathe abi lk wtr 2022 analysis 2.1 funktion f0

Abb. 1

(2 BE)

Weise nach, dass für $a\neq0$ alle Graphen $G_a$ einen gemeinsamen und einen weiteren, nicht gemeinsamen Wendepunkt haben.

(5 BE)

Ermittle den Wert $z$ mit $z \in \mathbb R$ so, dass gilt $\displaystyle\int_{-z}^{z}f_0(x)\;\mathrm dx=5000$ .
Erläutere mit Hilfe des Funktionsterms von $f_a,$ dass für alle $a$ und beliebige $z$ gilt: $\displaystyle\int_{-z}^{z}f_a(x)\;\mathrm dx= \displaystyle\int_{-z}^{z}f_0(x)\;\mathrm dx$ .

(4 BE)

Es gibt einen Wert $k \in \mathbb{R}$ , so dass gilt $\(f$ . Bestimme diesen Wert von $k$ .
Begründe ohne Rechnung, dass die Funktion $f_6$ keine Extremstelle bei $x=k$ hat.

(5 BE)

Ermittle den Wertebereich der Funktion $f_6$ .

(2 BE)

Eine ganzrationale Funktion $g$ dritten Grades hat folgende Eigenschaften:

Der Graph der Funktion $g$ verläuft durch den Koordinatenursprung.
Die Funktion $g$ hat in der Nullstelle $-2$ den Anstieg $-5$ .
Die Tangente an den Graphen der Funktion $g$ im Punkt $(2\mid g(2))$ verläuft parallel zur Geraden mit der Gleichung $y=-9x+9$ .

Bestimme eine Funktionsgleichung von $g$ .

$\bigg($ Zur Kontrolle: $g(x)=-\dfrac{3}{4}x^3-\dfrac{1}{2}x^2+2x$ $\bigg)$

(4 BE)

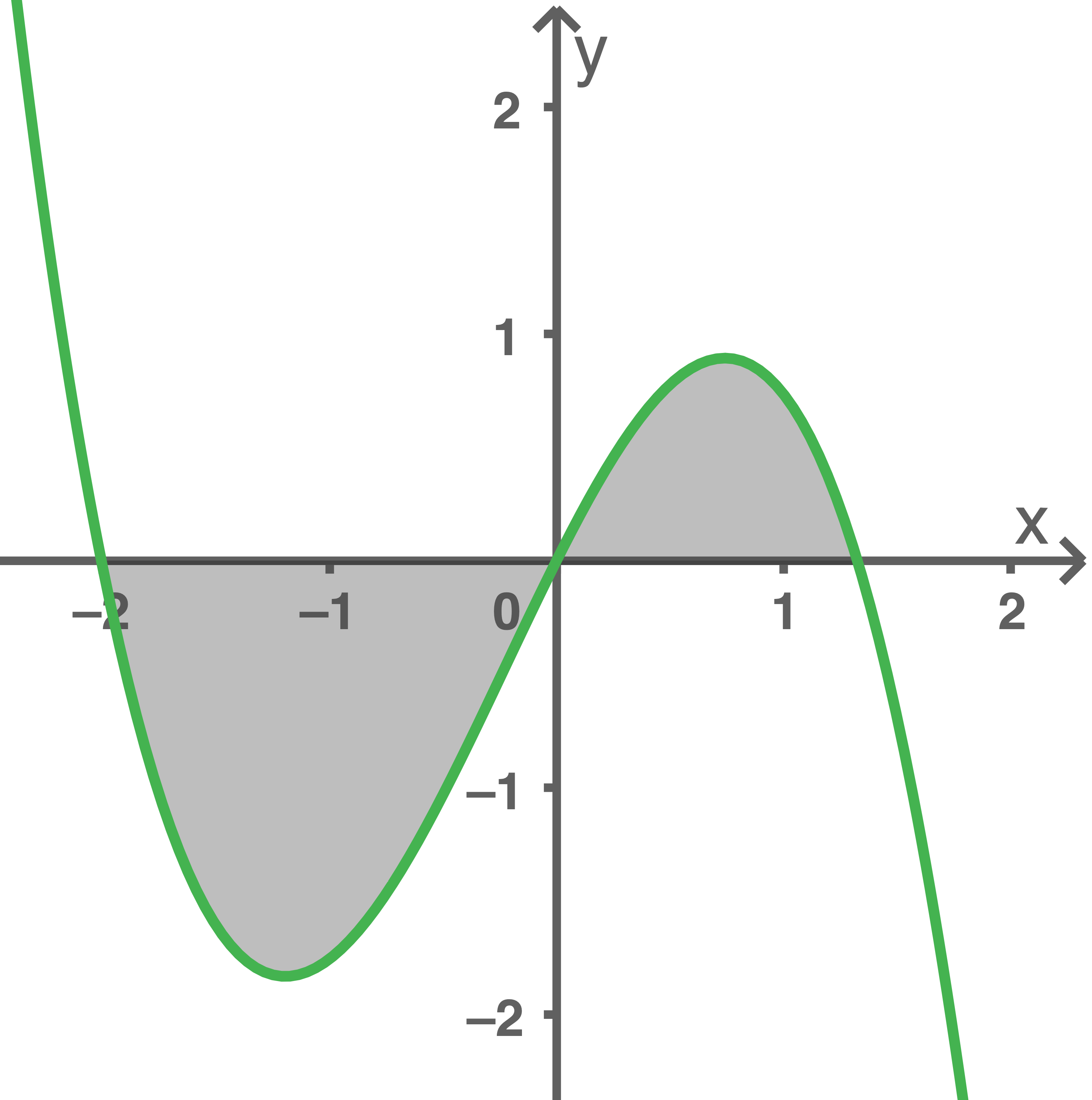
Die Abbildung 2 stellt den Graphen der Funktion $g$ aus Teilaufgabe j dar. Die Funktion $g$ hat drei Nullstellen:
$x_1=-2;x_2=0;x_3=\dfrac{4}{3}$ .

be abi lk wtr 2022 analysis 2.1 abbildung 2 integral

Abb. 2

Es gilt $\displaystyle\int_{-1}^{1}g(x)\;\mathrm dx=-\dfrac{1}{3}$ . Erläutere unter Zuhilfenahme der Abbildung 2 die geometrische Bedeutung dieser Gleichung.

(3 BE)

Entscheide für jede der folgenden Aussagen, ob sie richtig ist. Begründe deine Entscheidung.

$\,\text{I}$

$g$

$\,\text{II}$

$g$

$x$

(4 BE)

Weise nach, dass der Punkt $(2\mid f_{15}(2))$ ein Berührpunkt der Graphen von $f_{15}$ und $g$ ist.

(2 BE)

Bestimme die Werte des Parameters $a$ , für die gilt:
Die Graphen der Funktionen $f_a$ und $g$ haben genau einen gemeinsamen Punkt.

(4 BE)

(50 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$\lim\limits_{x \rightarrow +\infty} f_0(x)=+\infty$

$\lim\limits_{x \rightarrow -\infty} f_0(x)=+\infty$

1. Schritt: Ableitungen bilden

$f_0(x)=\dfrac{1}{8} x^4+2 x$

$\( f_0$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} f_0$

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$f_0^{\prime \prime}(-1,6) \approx 3,8>0$

Es gilt:

$f_0(-1,6)=\dfrac{1}{8} \cdot(-1,6)^4+2 \cdot(-1,6) \approx-2,4$

Daraus folgen die Koordinaten des lokalen Tiefpunktes mit $T(-1,6 \mid -2,4).$

Die allgemeinte Tangentengleichung an der Stelle $x_0$ lautet $\(t(x)=f$

$f_0(0)=0$
$\(f$

Die Tangentengleichung ist somit gegeben durch $t_0(x)=2\cdot (x-0)+0=2x.$

Für alle $a \in \mathbb{R}$ ist $f_{a}(0)=0$ und $\(f_a$ , also ist $t_0$ für alle Graphen $G_a$ die Tangente im Schnittpunkt mit der $y$ -Achse.

Da die Tangente parallel zu $t_0$ sein soll, muss $\(f$ gelten:

$\(\begin{array}[t]{rll} f$

Wegen $x\neq0$ gilt mit dem Satz vom Nullprodukt $x=\dfrac{a}{2}.$

$f_a\left(\dfrac{a}{2}\right)=a-\dfrac{a^4}{384}$

Die Tangente an den Graphen $G_a$ im Punkt $B$ ist somit gegeben durch $t_a(x)=2\cdot\left(x-\dfrac{a}{2}\right)+a-\dfrac{a^4}{384}$ $=2x-\dfrac{a^4}{384}.$

Der Abstand der beiden Tangenten lässt sich berechnen, indem die Normale an eine der Geraden berechnet wird. Anschließend wird der Abstand der Schnittpunkte beider Tangenten mit der Normale berechnet.

Die Normale an $t_0$ im Ursprung ist gegeben durch $n_0=-\dfrac{1}{2}x.$ Der Schnittpunkt mit $t_a$ wird wie folgt berechnet:

$\begin{array}[t]{rll} n_0(x)&=& t_a(x) \\[5pt] -\dfrac{1}{2}x &=& 2x-\dfrac{a^4}{384} \end{array}$

Der solve-Befehl des CAS liefert $x=\dfrac{a^4}{960}.$ Eingesetzt in die Normalengleichung folgt $y=-\dfrac{a^4}{1920}.$

Der Abstand vom Ursprung zu dem Punkt mit den gerade berechneten Koordinaten lässt sich wie folgt berechnen:

$\begin{array}[t]{rll} d(a) &=& \sqrt{\left(\dfrac{a^4}{960}\right)^2+\left(-\dfrac{a^4}{1920}\right)^2} \\[5pt] &=& \dfrac{a^4\cdot \sqrt{5}}{1920} \end{array}$

Es soll $d(a)=1920\cdot \sqrt{5}$ gelten.

Es folgt $\dfrac{a^4\cdot \sqrt{5}}{1920} = 1920\cdot \sqrt{5}$ und mit dem solve-Befehl des CAS $a \approx \pm 43,82.$

Die gesuchten Werte für $a$ sind $a_1\approx 43,82$ und $a_2\approx -43,82.$

Die zweite Ableitungsfunktion von $f_0$ ändert in der Umgebung von $x=0$ nicht das Vorzeichen, da der Graph oberhalb der $x$ -Achse liegt.

1. Schritt: Ableitungen bilden

$\(f_a$

2. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} f_a$

Mit dem Satz vom Nullprodukt folgt $x_1=0$ und:

$\begin{array}[t]{rll} \dfrac{3}{2}x -\dfrac{a}{2} &=& 0&\quad \scriptsize \mid\;+\dfrac{a}{2} \\[5pt] x&=& \dfrac{a}{2}&\quad \scriptsize \mid\;\cdot \dfrac{2}{3} \\[5pt] x&=&\dfrac{a}{3} \end{array}$

$x_2=\dfrac{a}{3}$

3. Schritt: Hinreichende Bedingung für Wendestellen anwenden

$\(f_a$ für $a \neq 0$

Es gibt folglich für $a \neq 0$ zwei Wendepunkte.

$W_1(0 \mid 0)$ ist ein Wendepunkt aller Graphen der Schar und $W _2\left(\dfrac{a}{3} \mid f_a\left(\dfrac{a}{3}\right)\right)$ ein von $a$ abhängiger Wendepunkt der Graphen der Schar.

Das integral wird mit dem CAS gelöst:

Rechenweg anzeigen

$\displaystyle\int_{-z}^{z}f_0(x)\;\mathrm dx= \dfrac{z^5}{20}$

Es muss also $\dfrac{z^5}{20}=5000$ gelten. Mit dem solve-Befehl des CAS folgt $z=10.$

Der Parameter $a$ in $f_a$ wirkt nur auf den Term mit dem Exponenten 3. Der Term ist also ungerade und somit punktsymmetrisch zum Ursprung. Damit gilt für alle Werte von $a:$ $\displaystyle\int_{-z}^{z}-\dfrac{a}{12}x^3\;\mathrm dx=0.$ Somit verändert der Term in $f_a,$ der von $a$ abhängig ist, das Integral über $f_a$ nicht und es gilt $\displaystyle\int_{-z}^{z}f_a(x)\;\mathrm dx=\displaystyle\int_{-z}^{z}f_0(x)\;\mathrm dx.$

Gleichung anzeigen

$\dfrac{1}{2}(x-k)^2\cdot (x+1)=\, ...$

Dieser Term soll nun gleich $\(f$ sein.

Mit Koeffizientenvergleich gilt:

$\dfrac{1}{2}-k=-\dfrac{3}{2}$

$\dfrac{1}{2}k^2-k=k$

$\dfrac{1}{2}k^2=\dfrac{1}{2}k^2$

Alle Gleichungen sind für $k=2$ erfüllt, dies ist also der gesuchte Wert.

Es gilt $\(f$ Da der Term für $x\geq -1$ keine negativen Werte annehmen kann, wechselt $\(f_6$ das Vorzeichen in der Umgebung von $x=2$ nicht. Daher kann dort auch keine Extremstelle vorliegen.

Der CAS liefert das Minimum $\left(-1\mid -\dfrac{11}{8}\right).$

Da die Funktionswerte für $x\rightarrow \pm \infty$ gegen $\infty$ verlaufen, ist der Wertebereich von $f_6$ gegeben durch $W=\left\{y\in \mathbb R \,\bigg \vert \, y\geq -\dfrac{11}{8}\right\}.$

$g(x)=a x^3+b x^2+c x+d$

$\(g$

Es gilt:

$g(0)=0$

$g(-2)=0$

$\( g$

Daraus ergibt sich das LGS:

Rechenweg anzeigen

Mit dem CAS ergibt sich $a=-\dfrac{3}{4};$ $b=-\dfrac{1}{2};$ $c=2$ und $d=0.$ Daraus erhält man die Funktionsgleichung $g(x)=-\dfrac{3}{4} x^3-\dfrac{1}{2} x^2+2 x.$

Das bestimmte Integral gibt die Flächenbilanz im Intervall $[-1 ; 1]$ an. Innerhalb dieses Intervalls hat die Funktion $g$ die Nullstelle $x=0.$ Da der Wert des bestimmten Integrals negativ ist, bedeutet dies, dass das Flächenstück unterhalb der $x$ -Achse größer ist als das Flächenstück oberhalb der $x$ -Achse.

Die Aussage I ist richtig. Nur an den beiden Nullstellen $x=-2$ und $x=\dfrac{4}{3}$ hat die Funktion $g$ einen Vorzeichenwechsel von positiv zu negativ. Der Graph jeder Stammfunktion von $g$ wechselt dort von steigend zu fallend, hat also zwei Hochpunkte.

Die Aussage II ist falsch. Jede Stammfunktion von $g$ ist eine Funktion 4. Grades mit einem negativen Koeffizienten vor $x^4.$ Die Integrationskonstante kann so gewählt werden, dass der Graph der Stammfunktion soweit nach unten verschoben wird bis er mit seinen zwei Hochpunkten unterhalb der $x$ -Achse verläuft.

$g(2)=-\dfrac{3}{4}\cdot 2^3-\dfrac{1}{2}\cdot 2^2+2\cdot 2=-4$
$f_{15}(2)=\dfrac{1}{8}\cdot 2^4 -\dfrac{15}{12}\cdot 2^3+2\cdot 2=-4$

$\(g$
$\(g$

$\(f_{15}$
$\(f_{15}$

Damit ist der Punkt $(2\mid -4)$ ein Berührpunkt der Graphen von $f_{15}$ und $g.$

Gleichung anzeigen

$f_a(x)=g(x)$

Der solve-Befehl des CAS liefert $x_1=0,\,\,\,$ $x_2=\dfrac{a-9}{3}+\sqrt{a^2-18a+45}$ und $x_3=\dfrac{a-9}{3}-\sqrt{a^2-18a+45}.$

Die Gleichung $a^2-18a+45=0$ hat die Lösungen $a_1=3$ und $a_2=15.$ Zwischen den beiden Nullstellen nimmt der Term negative Werte an. Da die Wurzel einer negativen Zahl in den reellen Zahlen nicht definiert ist, gibt es im Intervall $(3;15)$ keinen gemeinsamen Punkt außer $x_1=0.$

Die beiden Funktionen haben also für $3\lt a \lt 15$ genau einen gemeinsamen Punkt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?