Analysis 2.2 - Plutonium
Analysis: Plutonium
1
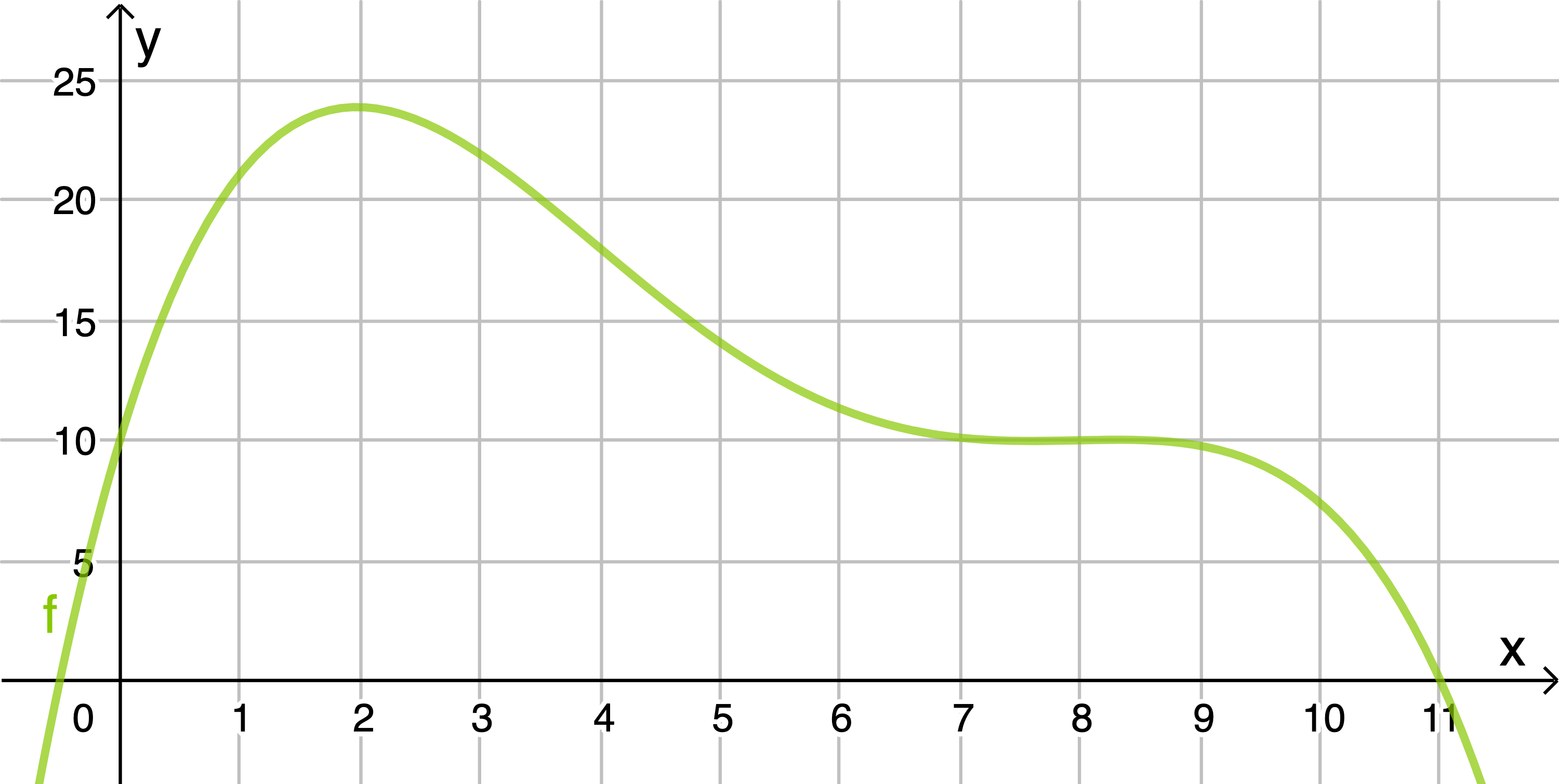
Die Abbildung 1 zeigt den Graphen einer in  definierten ganzrationalen Funktion
definierten ganzrationalen Funktion  vierten Grades.
vierten Grades.
Die Tangente im Wendepunkt des Graphen hat die Steigung
des Graphen hat die Steigung 
Die Tangente im Wendepunkt
a)
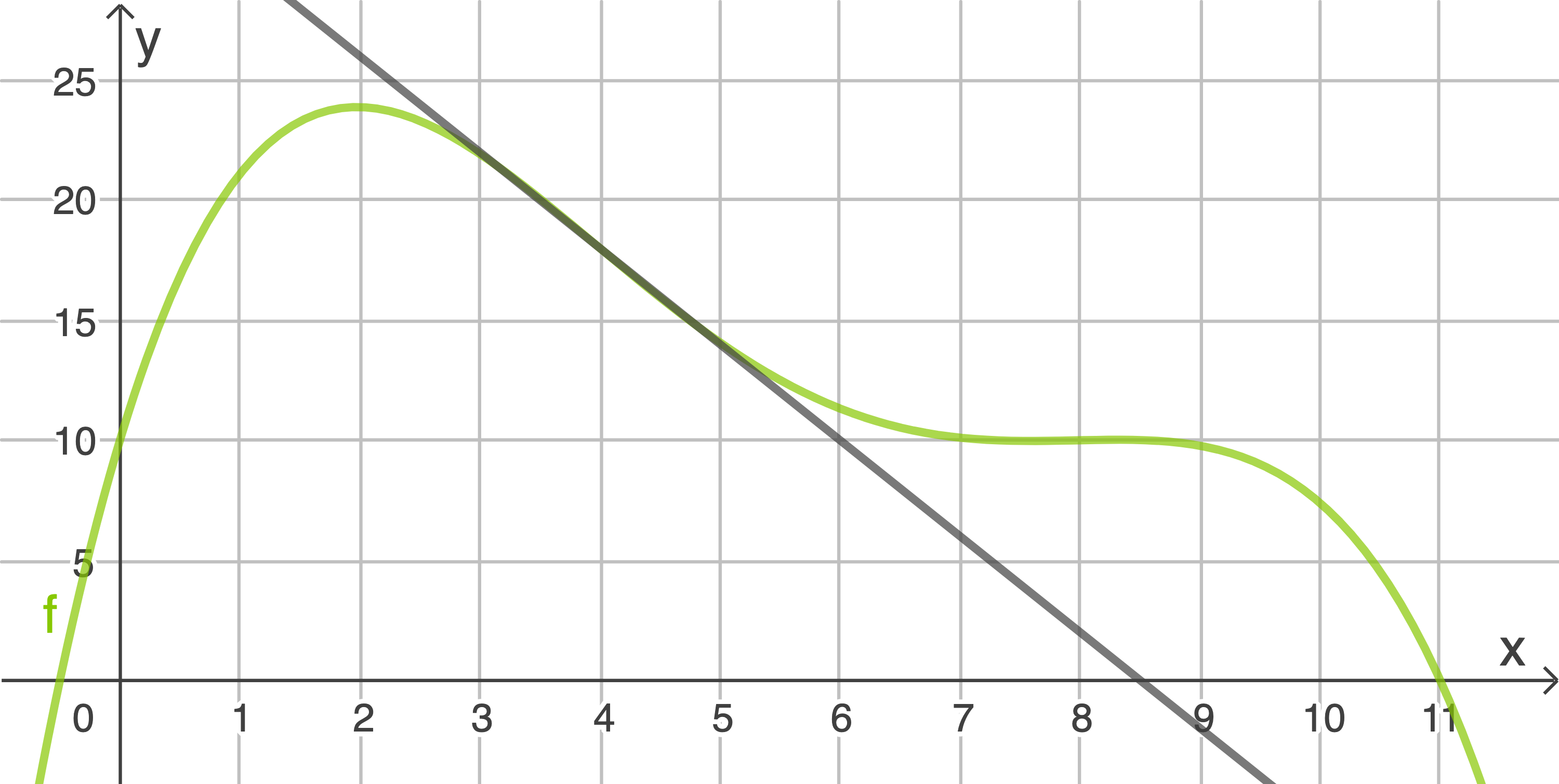
Zeichne die beschriebene Tangente in die Abbildung 1 ein.
Gib die beiden Nullstellen der ersten Ableitungsfunktion von
von  an.
an.
Gib die beiden Nullstellen der ersten Ableitungsfunktion
(3 BE)
b)
Der Graph von  hat einen Tiefpunkt.
hat einen Tiefpunkt.
Gib die Koordinaten dieses Tiefpunkts an und begründe deine Angabe.
Gib die Koordinaten dieses Tiefpunkts an und begründe deine Angabe.
(3 BE)
c)
Beurteile die folgende Aussage:
Für jede Stammfunktion  von
von  gilt
gilt  für jeden Wert von
für jeden Wert von ![\(x\in \left[0;5\right].\)](https://mathjax.schullv.de/f6d36ae9d90fbfcc67751dcc3f1bcc6192c0b6fea0dcbab2892de50ccdafd3cd?color=5a5a5a)
(3 BE)
2
Für jeden Wert von  wird die in
wird die in  definierte Funktion
definierte Funktion  mit
mit
 betrachtet. Der Graph von
betrachtet. Der Graph von  wird mit
wird mit  bezeichnet.
bezeichnet.
Für die erste Ableitungsfunktion von
von  gilt
gilt 
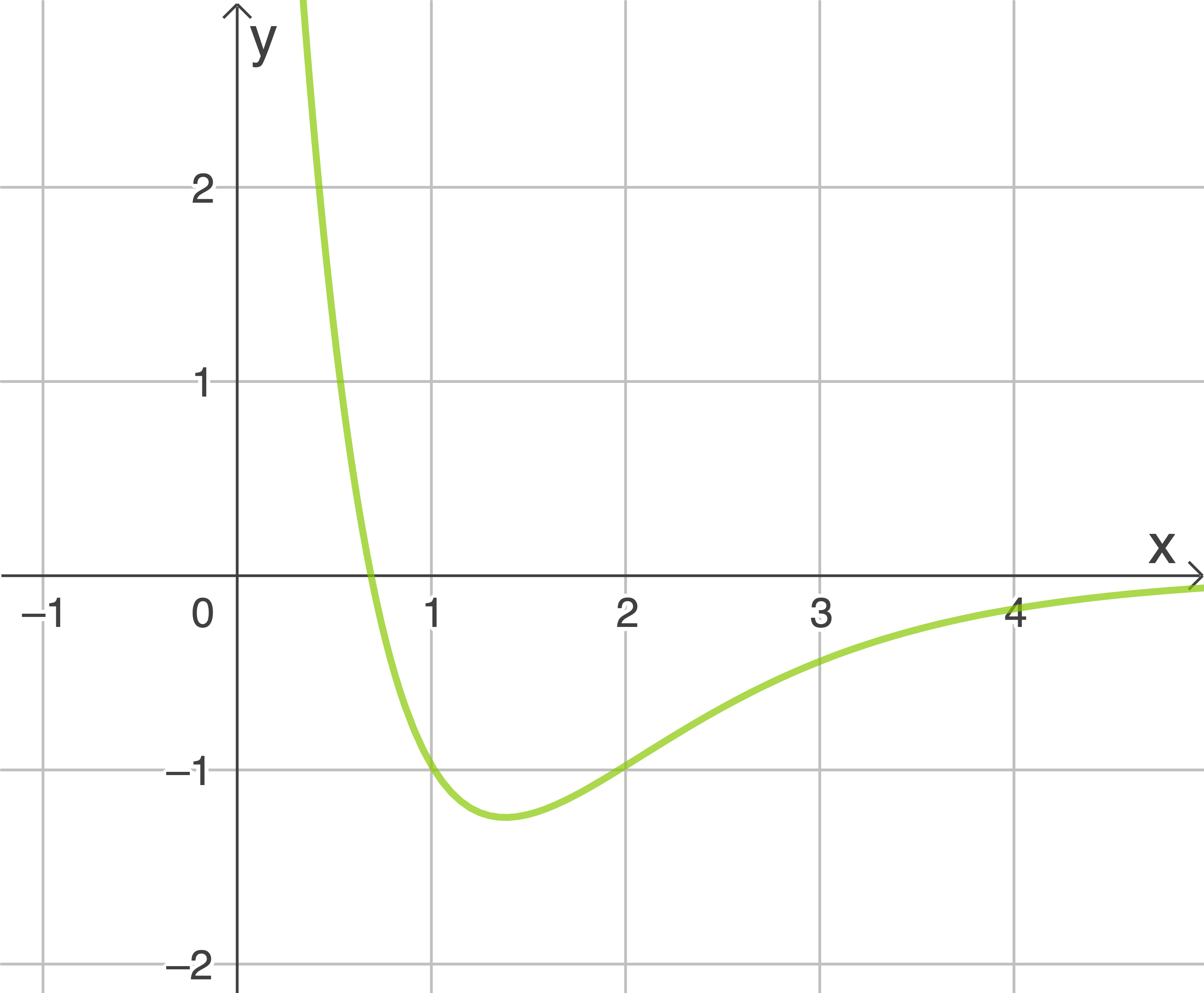
Die Abbildung 2 zeigt den Graphen der ersten Ableitungsfunktion von
Für die erste Ableitungsfunktion
Die Abbildung 2 zeigt den Graphen der ersten Ableitungsfunktion von
a)
Begründe, dass  nur die Nullstelle
nur die Nullstelle  hat.
hat.
Gib den Grenzwert von für
für  an.
an.
Gib den Grenzwert von
(3 BE)
b)
Begründe mithilfe des abgebildeten Graphen (Abb. 2), dass der Extrempunkt von  ein Hochpunkt ist.
ein Hochpunkt ist.
(2 BE)
c)
Bestimme die Koordinaten des Hochpunkts von  .
.
(2 BE)
d)
Betrachtet werden die Tangente an  im Koordinatenursprung und die Gerade, die zu dieser Tangente im Koordinatenursprung senkrecht steht. Diese beiden Geraden schneiden die Gerade mit der Gleichung
im Koordinatenursprung und die Gerade, die zu dieser Tangente im Koordinatenursprung senkrecht steht. Diese beiden Geraden schneiden die Gerade mit der Gleichung  Zeige rechnerisch, dass der Abstand der beiden Schnittpunkte
Zeige rechnerisch, dass der Abstand der beiden Schnittpunkte  ist.
ist.
(5 BE)
e)
Betrachtet man den Abstand  aus Teilaufgabe 2d) für alle Werte von
aus Teilaufgabe 2d) für alle Werte von  so ist dieser für einen Wert von
so ist dieser für einen Wert von  am kleinsten.
am kleinsten.
Bestimme diesen Wert und gib den zugehörigen Abstand an.
Bestimme diesen Wert und gib den zugehörigen Abstand an.
(3 BE)
f)
Durch den Koordinatenursprung, den Punkt  und den Punkt
und den Punkt  auf dem Graphen von
auf dem Graphen von  wird ein Dreieck festgelegt.
wird ein Dreieck festgelegt.
Ermittle eine Funktionsgleichung für die Funktion mit der der Flächeninhalt des Dreiecks
mit der der Flächeninhalt des Dreiecks  in Abhängigkeit von
in Abhängigkeit von  berechnet werden kann.
berechnet werden kann.
Ermittle eine Funktionsgleichung für die Funktion
(3 BE)
3
Am  April
April  ereignete sich in der Ukraine ein Reaktorunfall, bei dem radioaktives Plutonium-
ereignete sich in der Ukraine ein Reaktorunfall, bei dem radioaktives Plutonium- freigesetzt wurde. Plutonium-
freigesetzt wurde. Plutonium- zerfällt exponentiell, d.h. in jedem Jahr nimmt die Masse des vorhandenen Plutonium-
zerfällt exponentiell, d.h. in jedem Jahr nimmt die Masse des vorhandenen Plutonium- um einen konstanten prozentualen Anteil ab.
Im Folgenden wird der Zerfall einer bestimmten Menge Plutonium-
um einen konstanten prozentualen Anteil ab.
Im Folgenden wird der Zerfall einer bestimmten Menge Plutonium- betrachtet. Dieser Zerfall wird durch die Funktion
betrachtet. Dieser Zerfall wird durch die Funktion  mit
mit  und
und  beschrieben.
beschrieben.
Dabei ist die Zeit in Jahren, die seit dem Reaktorunfall vergangen ist, und
die Zeit in Jahren, die seit dem Reaktorunfall vergangen ist, und  die Masse des verbliebenen Plutonium-
die Masse des verbliebenen Plutonium- in Milligramm.
in Milligramm.
 entsteht radioaktives Americium-
entsteht radioaktives Americium- , das ebenfalls exponentiell zerfällt. Im verwendeten Modell gibt die Funktion
, das ebenfalls exponentiell zerfällt. Im verwendeten Modell gibt die Funktion  mit
mit  für jedes Jahr die Masse des vorhandenen Americium-
für jedes Jahr die Masse des vorhandenen Americium- in Milligramm an.
in Milligramm an.
Dabei ist
a)
Gib die Bedeutung des Faktors  im Sachzusammenhang an und berechne den prozentualen Anteil, um den die Masse des Plutonium-
im Sachzusammenhang an und berechne den prozentualen Anteil, um den die Masse des Plutonium- in jedem Jahr abnimmt.
in jedem Jahr abnimmt.
(3 BE)
b)
Bestimme das Jahr, in dessen Verlauf erstmals weniger als ein Milligramm des Plutonium- vorhanden sein wird.
vorhanden sein wird.
Bei dem Zerfall des Plutonium-
(3 BE)
c)
Der Graph von  kann für einen Wert von
kann für einen Wert von  aus dem Graphen der Funktion
aus dem Graphen der Funktion  aus Aufgabe 2 erzeugt werden, indem man diesen in
aus Aufgabe 2 erzeugt werden, indem man diesen in  -Richtung und in
-Richtung und in  -Richtung streckt.
-Richtung streckt.
Gib die beiden Streckungsfaktoren an und bestimme den passenden Wert von
Gib die beiden Streckungsfaktoren an und bestimme den passenden Wert von
(3 BE)
d)
Gib die Bedeutung der Aussage  im Sachzusammenhang an.
im Sachzusammenhang an.
Begründe deine Angabe.
Begründe deine Angabe.
(4 BE)
(40 BE)
Analysis: Plutonium
1
a)
Tangente einzeichnen:
Nullstellen von angeben:
angeben:
Die beiden Nullstellen der ersten Ableitungsfunktion von
von  befinden sich bei
befinden sich bei  und
und  .
.
Nullstellen von
Die beiden Nullstellen der ersten Ableitungsfunktion
b)
Koordinaten des Tiefpunktes des Graphen von  angeben:
angeben:
Aus der Aufgabenstellung folgt, dass die Steigung im Wendepunkt beträgt. In unmittelbarer Umgebung vom Wendepunkt
beträgt. In unmittelbarer Umgebung vom Wendepunkt  ist die Steigung des Graphen von
ist die Steigung des Graphen von  größer als
größer als  .
.
Daraus folgt, dass der Graph von den Tiefpunkt
den Tiefpunkt  hat.
hat.
Aus der Aufgabenstellung folgt, dass die Steigung im Wendepunkt
Daraus folgt, dass der Graph von
c)
Aussage beurteilen:
Die Aussage ist richtig.
Für jeden Wert![\(x_0\in[0;5]\)](https://mathjax.schullv.de/5bea8d390a4b676bcffeb89624824c5d14e4869e44c01cc9c2a2c020f36c6a4c?color=5a5a5a) ist
ist  der Inhalt der Fläche, die der Graph von
der Inhalt der Fläche, die der Graph von  mit der
mit der  -Achse und den Geraden mit den Gleichungen
-Achse und den Geraden mit den Gleichungen  und
und  einschließt. Der Inhalt dieser Fläche ist für jeden dieser Werte von
einschließt. Der Inhalt dieser Fläche ist für jeden dieser Werte von  größer als der Flächeninhalt eines Rechtecks mit den Seitenlängen
größer als der Flächeninhalt eines Rechtecks mit den Seitenlängen ![\(2\,[\text{LE}]\)](https://mathjax.schullv.de/9e7f47caaef508666a5b08195264339b7d198610a2b6fb9cc04a5d83e0637b1e?color=5a5a5a) und
und ![\(10\,[\text{LE}]\)](https://mathjax.schullv.de/7c4a838da99f79187bf350792a609f6c9cfe809cf136e9497ce0ae930a6b2afc?color=5a5a5a) , das heißt größer als
, das heißt größer als ![\(20\,[\text{FE}]\)](https://mathjax.schullv.de/f4522fabddfa25c499d7b1def4a7b5af8915b0368a4a578f2fabc57f625621b4?color=5a5a5a) .
.
Die Aussage ist richtig.
Für jeden Wert
2
a)
Nullstelle von  begründen:
begründen:
![\(\begin{array}[t]{rll}
h_k(x)&=& 0&\\[5pt]
10\cdot(1-\mathrm{e}^{-kx})\cdot \mathrm{e}^{-x}&=& 0& \quad\scriptsize (\mathrm{e}^{-x}\neq 0 \,\text{für alle} \, x)\\[5pt]
1-\mathrm{e}^{-kx}&=&0& \quad\scriptsize (\mathrm{e}^0=1) \\[5pt]
x&=& 0
\end{array}\)](https://mathjax.schullv.de/26bc9da1fd00ce557f1a7158d59e4bd869b7ddb01b7cc2ce9ebbfc9459c6da2e?color=5a5a5a)
Daraus folgt, dass nur die Nullstelle
nur die Nullstelle  hat.
hat.
Grenzwert von für
für  bestimmen:
bestimmen:
![\(\begin{array}[t]{rll}
\lim\limits_{x\to+\infty}h_k(x)&=& 0
\end{array}\)](https://mathjax.schullv.de/dfd2e4a758cf0c12023e74123a490c3acd59cc18502f3d20933f9e74e341aa32?color=5a5a5a)
Daraus folgt, dass
Grenzwert von
b)
Art des Extrempunktes von  begründen:
begründen:
Monotonieverhalten analysieren: Für alle gilt:
gilt:  ist monoton wachsend.
ist monoton wachsend.
Für alle gilt:
gilt:  ist monoton fallend.
Daraus folgt für den Graphen
ist monoton fallend.
Daraus folgt für den Graphen  (Graph der ersten Ableitungsfunktion von
(Graph der ersten Ableitungsfunktion von  ):
):
 hat einen Vorzeichenwechsel von
hat einen Vorzeichenwechsel von  nach
nach  .
.
Damit ist bewiesen, dass der Extrempunkt von ein Hochpunkt ist.
ein Hochpunkt ist.
Monotonieverhalten analysieren: Für alle
Für alle
Damit ist bewiesen, dass der Extrempunkt von
c)
Koordinaten des Hochpunktes von  bestimmen:
bestimmen:
Notwendige Bedingung: Alternativ kannst du die Lösung auch mit deinem CAS berechnen.
Setze
Alternativ kannst du die Lösung auch mit deinem CAS berechnen.
Setze  in
in  ein:
ein:
Die Koordinaten des Hochpunktes von lauten
lauten
 .
.
Notwendige Bedingung:
Die Koordinaten des Hochpunktes von
d)
Abstand der beiden Schnittpunkte bestimmen:
Steigung der Tangente an im Koordinatenursprung:
im Koordinatenursprung:
![\(\begin{array}[t]{rll}
h](https://mathjax.schullv.de/3d7de9c83f3e66d22444a1f62628a15c2dcfa3f2f739e51a17fd8d82674d4ce7?color=5a5a5a) Die Tangente hat die Steigung
Die Tangente hat die Steigung  .
Für zueinander senkrechte Geraden gilt:
.
Für zueinander senkrechte Geraden gilt:
 Daher beträgt die Steigung der senkrechten Gerade zur Tangente
Daher beträgt die Steigung der senkrechten Gerade zur Tangente  .
Schnittpunkte mit der Geraden
.
Schnittpunkte mit der Geraden  :
:
 und
und  Abstand der Schnittpunkte:
Der Abstand der beiden Schnittpunkte
Abstand der Schnittpunkte:
Der Abstand der beiden Schnittpunkte  entspricht der Länge der Strecke
entspricht der Länge der Strecke  Damit ist bewiesen, dass der Abstand der beiden Schnittpunkte
Damit ist bewiesen, dass der Abstand der beiden Schnittpunkte  ist.
ist.
Steigung der Tangente an
e)
Koordinaten des Tiefpunktes des Graphen von  bestimmen:
bestimmen:
Der Tiefpunkt kann mit Hilfe eines CAS-Taschenrechners bestimmt werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Der Tiefpunkt des Graphen von
Casio Classpad II
Der Tiefpunkt des Graphen von  befindet sich bei
befindet sich bei  .
Für
.
Für  ist der Abstand der beiden Schnittpunkte aus Teilaufgabe 2d) am kleinsten.
ist der Abstand der beiden Schnittpunkte aus Teilaufgabe 2d) am kleinsten.
Der Abstand der beiden Schnittpunkte beträgt![\(d\left(\dfrac{1}{10}\right)=2 \,[\text{LE}]\)](https://mathjax.schullv.de/c1324a728966ba34b0916f8daa2849e750735a1786971307b633c6430b726a39?color=5a5a5a) .
.
Der Tiefpunkt kann mit Hilfe eines CAS-Taschenrechners bestimmt werden.
menu  6: Graph analysieren
6: Graph analysieren  2: Minimum
2: Minimum
Analyse  Grafische Lösung
Grafische Lösung  Minimum
Minimum
Der Abstand der beiden Schnittpunkte beträgt
f)
Funktionsgleichung für die Funktion  ermitteln:
ermitteln:

![\(\begin{array}[t]{rll}
A(u)&=& \dfrac{1}{2}\cdot u\cdot10(1- \mathrm e^{-u})\cdot \mathrm e^{-u} \\[5pt]
&=& 5\cdot u \cdot(\mathrm e^{-u}- \mathrm e^{-2u})
\end{array}\)](https://mathjax.schullv.de/51cfecdfbeb2c38ad28b886b2d78a81d5a642c396c10f4fcb93e768a368166fe?color=5a5a5a)
3
a)
Bedeutung des Faktor  angeben:
angeben:
Der Faktor gibt die Masse zum Zeitpunkt des Unfalls in Milligramm an.
gibt die Masse zum Zeitpunkt des Unfalls in Milligramm an.
Prozentualen Anteil berechnen:

 Jährlich nimmt die Masse um etwa
Jährlich nimmt die Masse um etwa  ab.
ab.
Der Faktor
Prozentualen Anteil berechnen:
b)
Jahr bestimmen:
 Im Jahr
Im Jahr  wird erstmals weniger als ein Milligramm des Plutonium-
wird erstmals weniger als ein Milligramm des Plutonium- vorhanden sein.
vorhanden sein.
c)
Streckungsfaktoren und Wert von  bestimmen:
bestimmen:

 Streckungsfaktor in
Streckungsfaktor in  -Richtung:
-Richtung:
 Streckungsfaktor in
Streckungsfaktor in  -Richtung:
-Richtung:
 Wert von
Wert von  :
:

d)
Bedeutung der Aussage  angeben:
angeben:
Die Masse des Americium- nimmt in den ersten
nimmt in den ersten  Jahren nach dem Reaktorunfall im Mittel pro Jahr um
Jahren nach dem Reaktorunfall im Mittel pro Jahr um  Milligramm zu.
Milligramm zu.
Begründen können wir die Aussage damit, dass die mittlere Änderung pro Jahr beträgt, wobei
beträgt, wobei  gilt. Da der Wert des gegebenen Terms positiv ist, handelt es sich bei der Änderung um eine Zunahme.
gilt. Da der Wert des gegebenen Terms positiv ist, handelt es sich bei der Änderung um eine Zunahme.
Die Masse des Americium-
Begründen können wir die Aussage damit, dass die mittlere Änderung pro Jahr