Analysis 2.2 - Lesebestätigung
1
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit 

a)
Begründe, dass jeder Graph der Schar symmetrisch bezüglich des Koordinatenursprungs ist.
(2 BE)
b)
Weise in Abhängigkeit von  nach, dass der Graph von
nach, dass der Graph von  einen Tiefpunkt mit der
einen Tiefpunkt mit der  -Koordinate
-Koordinate  hat. Begründe, dass er zudem einen Hochpunkt besitzt und dass dieser eine kleinere
hat. Begründe, dass er zudem einen Hochpunkt besitzt und dass dieser eine kleinere  -Koordinate hat als der Tiefpunkt.
-Koordinate hat als der Tiefpunkt.
(4 BE)
c)
Beurteile folgende Aussage:

Betrachtet wird nun die Funktion der Schar
Es gibt einen Wert von  so dass die Strecke zwischen dem Hochpunkt und Tiefpunkt eine Diagonale eines achsenparallelen Quadrats ist.
so dass die Strecke zwischen dem Hochpunkt und Tiefpunkt eine Diagonale eines achsenparallelen Quadrats ist.
(3 BE)
d)
Die Tangente an den Graphen von  im Punkt
im Punkt  die
die  -Achse und die Gerade
-Achse und die Gerade  mit der Gleichung
mit der Gleichung  schließen ein Dreieck ein.
schließen ein Dreieck ein.
Berechne den Flächeninhalt des Dreiecks.
Berechne den Flächeninhalt des Dreiecks.
(5 BE)
e)
Der Graph von  und die
und die  -Achse begrenzen eine Fläche, die aus zwei Flächenstücken besteht.
-Achse begrenzen eine Fläche, die aus zwei Flächenstücken besteht.
Es gibt eine Gerade für die gilt:
für die gilt:
 an und begründe deine Angabe. Ermittle für das Flächenstück, das im zweiten Quadranten liegt, das Verhältnis der beiden Teilflächen.
an und begründe deine Angabe. Ermittle für das Flächenstück, das im zweiten Quadranten liegt, das Verhältnis der beiden Teilflächen.
Es gibt eine Gerade
- die Gerade
verläuft parallel zur Geraden
aus Teilaufgabe d
- die Gerade
teilt jedes der beiden Flächenstücke in zwei Teile
- das Verhältnis dieser beiden Teile ist in beiden Flächenstücken gleich groß.
(5 BE)
f)
Begründe, dass die folgende Aussage richtig ist:

Ist  ein beliebiger Punkt auf dem Graphen von
ein beliebiger Punkt auf dem Graphen von  so liegt der Mittelpunkt der Verbindungsstrecke von
so liegt der Mittelpunkt der Verbindungsstrecke von  und dem Koordinatenursprung auf dem Graphen der in
und dem Koordinatenursprung auf dem Graphen der in  definierten Funktion
definierten Funktion 
(4 BE)
g)
Betrachtet wird die Funktion  mit
mit  Für einen Wert von
Für einen Wert von  und einen Wert von
und einen Wert von  gelten folgende Bedingungen:
gelten folgende Bedingungen:
 und
und 
- Die Funktion
hat bei
eine Nullstelle,
- der Graph von
schließt im vierten Quadranten mit der
-Achse ein Flächenstück mit dem Inhalt
ein.
(4 BE)
2
Die Leitung eines großen Unternehmens versendet jeden Arbeitstag um  Uhr eine E-Mail mit tagesaktuellen Informationen an alle Mitarbeiterinnen und Mitarbeiter. Diese wurden gebeten, nach dem Lesen der E-Mail eine Lesebestätigung zu versenden.
Die folgende Tabelle zeigt für einen bestimmten Tag, wie viele Lesebestätigungen bei der Leitung des Unternehmens bis zum jeweiligen Zeitpunkt bereits eingegangen sind.
Uhr eine E-Mail mit tagesaktuellen Informationen an alle Mitarbeiterinnen und Mitarbeiter. Diese wurden gebeten, nach dem Lesen der E-Mail eine Lesebestätigung zu versenden.
Die folgende Tabelle zeigt für einen bestimmten Tag, wie viele Lesebestätigungen bei der Leitung des Unternehmens bis zum jeweiligen Zeitpunkt bereits eingegangen sind.
Beispielsweise sind von  Uhr bis
Uhr bis  Uhr
Uhr  Lesebestätigungen eingegangen.
Lesebestätigungen eingegangen.
 definierten Funktionen
definierten Funktionen  und
und  die Funktion
die Funktion  entwickelt:
entwickelt:
 Die Funktion
Die Funktion  beschreibt modellhaft für einen Zeitraum von acht Stunden eines Arbeitstages die zeitliche Entwicklung der momentanen Änderungsrate der Anzahl der eingegangenen Lesebestätigungen. Dabei ist
beschreibt modellhaft für einen Zeitraum von acht Stunden eines Arbeitstages die zeitliche Entwicklung der momentanen Änderungsrate der Anzahl der eingegangenen Lesebestätigungen. Dabei ist  die seit
die seit  Uhr vergangene Zeit in Stunden und
Uhr vergangene Zeit in Stunden und  die momentane Änderungsrate der Anzahl der seit
die momentane Änderungsrate der Anzahl der seit  Uhr eingegangenen Lesebestätigungen in der Einheit
Uhr eingegangenen Lesebestätigungen in der Einheit 
| Zeitpunkt | Anzahl der bis dahin eingegangenen Lesebestätigungen | |
|---|---|---|
| ..... | ||
| ..... | ||
a)
Ermittle mithilfe der Tabelle für den betrachteten Tag, wie viele Lesebestätigungen im Zeitraum von  Uhr bis
Uhr bis  Uhr im Mittel pro Stunde eingegangen sind.
Uhr im Mittel pro Stunde eingegangen sind.
Auf der Grundlage der über viele Tage erfassten Lesebestätigungen wurde mithilfe der in
(3 BE)
b)
Berechne  und interpretiere das Ergebnis im Sachzusammenhang.
und interpretiere das Ergebnis im Sachzusammenhang.
(3 BE)
c)
Es gilt  Begründe, dass die Funktion
Begründe, dass die Funktion  nicht geeignet ist, die momentane Änderungsrate auch für den Zeitraum nach
nicht geeignet ist, die momentane Änderungsrate auch für den Zeitraum nach  Uhr zu beschreiben.
Uhr zu beschreiben.
(3 BE)
d)
Berechne mithilfe der Funktion  die Anzahl der im Zeitraum von
die Anzahl der im Zeitraum von  Uhr bis
Uhr bis  Uhr eines Arbeitstages eingegangenen Lesebestätigungen. Ermittle, um wie viel Prozent diese auf der Grundlage des Modells berechnete Anzahl von der entsprechenden Anzahl des eingangs betrachteten Tages (vgl. Tabelle) abweicht.
Uhr eines Arbeitstages eingegangenen Lesebestätigungen. Ermittle, um wie viel Prozent diese auf der Grundlage des Modells berechnete Anzahl von der entsprechenden Anzahl des eingangs betrachteten Tages (vgl. Tabelle) abweicht.
(4 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1
a)
Für jeden Wert von  ist der Funktionsterm von
ist der Funktionsterm von  ein Polynom, welches nur ungerade Exponenten von
ein Polynom, welches nur ungerade Exponenten von  besitzt und somit symmetrisch zum Koordinatenursprung ist.
besitzt und somit symmetrisch zum Koordinatenursprung ist.
b)
Für die ersten beiden Ableitungen von  folgt mit dem CAS:
folgt mit dem CAS:

 1. Schritt: Notwendige Bedingung für Extremstellen überprüfen
1. Schritt: Notwendige Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
f_a](https://mathjax.schullv.de/91a07a9509eec47b883b77457460df457c1f228048e39223307490d818fad0d5?color=5a5a5a) 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
 Da
Da  gilt, ist dieser Wert größer als null, womit der Graph von
gilt, ist dieser Wert größer als null, womit der Graph von  einen Tiefpunkt mit der
einen Tiefpunkt mit der  -Koordinate
-Koordinate  hat. Da der Graph von
hat. Da der Graph von  punktsymmetrisch zum Ursprung ist, besitzt
punktsymmetrisch zum Ursprung ist, besitzt  somit bei
somit bei  einen Hochpunkt, der wegen
einen Hochpunkt, der wegen  eine kleinere
eine kleinere  -Koordinate als der Tiefpunkt hat.
-Koordinate als der Tiefpunkt hat.
c)
Für die  -Koordinate des Tiefpunkts von
-Koordinate des Tiefpunkts von  folgt:
Da der Graph der Schar punktsymmetrisch zum Ursprung ist, verläuft die Strecke zwischen dem Hoch- und dem Tiefpunkt durch den Ursprung und damit auf einer Geraden der Form
folgt:
Da der Graph der Schar punktsymmetrisch zum Ursprung ist, verläuft die Strecke zwischen dem Hoch- und dem Tiefpunkt durch den Ursprung und damit auf einer Geraden der Form  Einsetzen der Koordinaten des Tiefpunkts liefert mit dem solve-Befehl des CAS für
Einsetzen der Koordinaten des Tiefpunkts liefert mit dem solve-Befehl des CAS für 
 Da somit
Da somit  gilt, ist die Strecke für alle
gilt, ist die Strecke für alle  keine Diagonale eines achsenparallelen Quadrats und somit ist die Aussage falsch.
keine Diagonale eines achsenparallelen Quadrats und somit ist die Aussage falsch.
d)
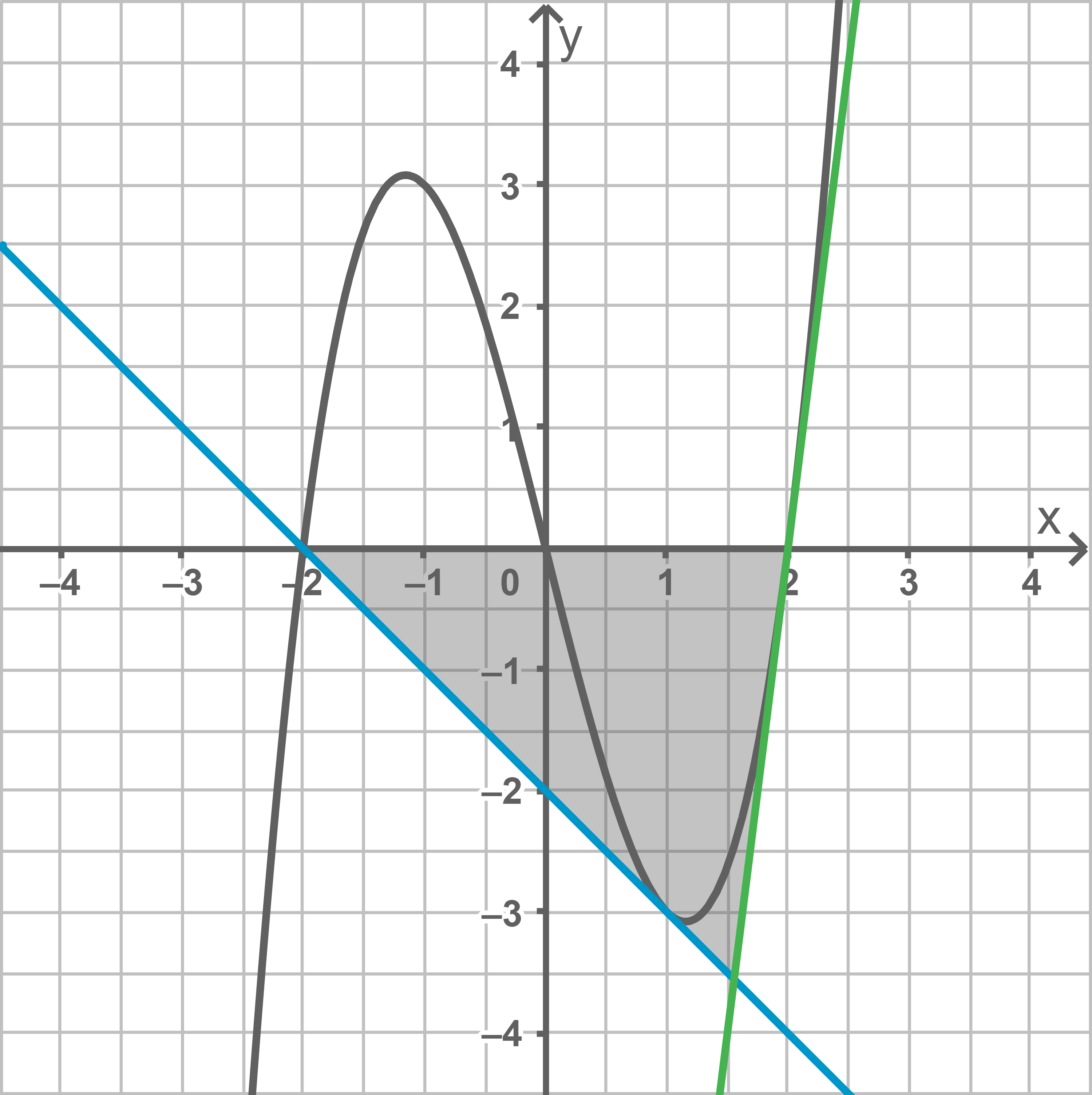
e)
Gleichung angeben und begründen
Die Gerade  hat die Gleichung
hat die Gleichung  denn da der Graph von
denn da der Graph von  symmetrisch zum Koordinatenurpsrung ist und
symmetrisch zum Koordinatenurpsrung ist und  parallel zu
parallel zu  verläuft, muss die Gerade
verläuft, muss die Gerade  durch den Ursprung verlaufen und Steigung
durch den Ursprung verlaufen und Steigung  besitzen.
Verhältnis ermitteln
Auflösen von
besitzen.
Verhältnis ermitteln
Auflösen von  nach
nach  mit dem solve-Befehl des CAS liefert:
mit dem solve-Befehl des CAS liefert:
![\(\begin{array}[t]{rll}
x_1&=&-\sqrt{3} \\[5pt]
x_2&=&0 \\[5pt]
x_3&=&\sqrt{3}
\end{array}\)](https://mathjax.schullv.de/bc62bcf8eed64b17495f4b47aebee32ace47ee6d3199a60b5c770865ad56107a?color=5a5a5a) Für den Inhalt des gesamten Flächenstücks im zweiten Quadranten folgt mit dem CAS:
Für den Inhalt des gesamten Flächenstücks im zweiten Quadranten folgt mit dem CAS:
![\(A=\displaystyle\int_{-2}^{0}f_1(x)\;\mathrm dx = 4\;[\text{FE}]\)](https://mathjax.schullv.de/f2da96b72fe8aa48e6740773afe4c72282e68696056566776f54ced99a45b773?color=5a5a5a) Für die Größe der durch den Schnitt der Geraden entstehenden Teilflächen folgt damit:
Für die Größe der durch den Schnitt der Geraden entstehenden Teilflächen folgt damit:
![\(A_1=\displaystyle\int_{-\sqrt{3}}^{0}(f_1(x)+x)\;\mathrm dx = \dfrac{9}{4}\;[\text{FE}]\)](https://mathjax.schullv.de/37ce9a5e7f643060506846194ab2123c8bf0628490fb68bc9183fea880819468?color=5a5a5a)
![\(A_2=4-\dfrac{9}{4}=\dfrac{7}{4}\;[\text{FE}]\)](https://mathjax.schullv.de/e81e6606376d6995f38a3526f5f2d0875d927076e7201a37b82d16451a8d56cc?color=5a5a5a) Für das Verhältnis der beiden Teilflächen ergibt sich somit:
Für das Verhältnis der beiden Teilflächen ergibt sich somit:

f)
Für einen Punkt  auf dem Graphen von
auf dem Graphen von  mit den allgemeinen Koordinaten
mit den allgemeinen Koordinaten  hat der Mittelpunkt der Verbindungsstrecke von
hat der Mittelpunkt der Verbindungsstrecke von  mit dem Koordinatenursprung die Koordinaten
mit dem Koordinatenursprung die Koordinaten  Gleichsetzen von
Gleichsetzen von  mit
mit  liefert:
liefert:
![\(\begin{array}[t]{rll}
f_4\left(\dfrac{x}{2}\right)&=&\dfrac{f_1(x)}{2} \\[5pt]
4\cdot\left(\dfrac{x}{2}\right)^3-4\cdot\dfrac{x}{2}&=&\dfrac{x^3-4x}{2} \\[5pt]
\dfrac{1}{2}x^3-2x&=&\dfrac{1}{2}x^3-2x
\end{array}\)](https://mathjax.schullv.de/e16b20e8038b51b80fd15b58ba282b8a4eec5632d315cbb57501d85af611c805?color=5a5a5a) Da die beiden Seiten der Gleichung übereinstimmen, ist die Aussage aus der Aufgabenstellung richtig.
Da die beiden Seiten der Gleichung übereinstimmen, ist die Aussage aus der Aufgabenstellung richtig.
g)
Für alle Werte von  und
und  besitzt die Funktion
besitzt die Funktion  an der Stelle
an der Stelle  eine Nullstelle. Die beiden angegebenen Bedingungen ergeben somit
eine Nullstelle. Die beiden angegebenen Bedingungen ergeben somit  und
und  Auflösen der ersten Bedingung nach
Auflösen der ersten Bedingung nach  mit dem CAS liefert:
mit dem CAS liefert:
 Einsetzen in die zweite Bedingung liefert für
Einsetzen in die zweite Bedingung liefert für  Die zu den beiden Bedingungen zugehörigen Werte ergeben sich somit zu
Die zu den beiden Bedingungen zugehörigen Werte ergeben sich somit zu  und
und 
2
a)
Die zeitliche Differenz zwischen  Uhr und
Uhr und  Uhr beträgt
Uhr beträgt  Stunden. Für die im Mittel pro Stunde eingegangenen Lesebestätigungen in diesem Zeitfenster folgt somit:
Stunden. Für die im Mittel pro Stunde eingegangenen Lesebestätigungen in diesem Zeitfenster folgt somit:

b)
c)
Anhand des Funktionsterms von  lässt sich erkennen, dass die Funktionswerte bei
lässt sich erkennen, dass die Funktionswerte bei  ihr Vorzeichen von plus nach minus ändern, da
ihr Vorzeichen von plus nach minus ändern, da  dort seine erste Nullstelle besitzt. Somit würden die Änderungsraten nach
dort seine erste Nullstelle besitzt. Somit würden die Änderungsraten nach  Uhr negative Werte annehmen, was im Sachzusammenhang keinen Sinn ergibt.
Uhr negative Werte annehmen, was im Sachzusammenhang keinen Sinn ergibt.
d)
Eingegangene Lesebestätigungen berechnen
Da die seit  Uhr vergangene Zeit um
Uhr vergangene Zeit um  Uhr
Uhr  Stunden beträgt, folgt:
Prozentuale Abweichung ermitteln
Mit den Werten aus der Tabelle folgt für die gesuchte prozentuale Abweichung:
Stunden beträgt, folgt:
Prozentuale Abweichung ermitteln
Mit den Werten aus der Tabelle folgt für die gesuchte prozentuale Abweichung:
