Stochastik 3.2 - Fitnessarmband

Unter den Kunden eines Krankenversicherungsunternehmens haben $59\,\%$ Datenschutzbedenken. Von den Kunden mit Datenschutzbedenken nutzen $23\,\%$ ein Fitnessarmband. $19\,\%$ aller Kunden haben keine Datenschutzbedenken und nutzen ein Fitnessarmband.

Stelle den Sachverhalt in einem beschrifteten Baumdiagramm dar.

(3 BE)

Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband.
Bestimme die Wahrscheinlichkeit dafür, dass sie Datenschutzbedenken hat.

(3 BE)

Es gilt $0,23\neq0,59\cdot 0,23+0,19$ . Begründe damit, dass die Ereignisse „Eine unter allen Kunden zufällig ausgewählte Person hat Datenschutzbedenken.“ und „Eine unter allen Kunden zufällig ausgewählte Person nutzt ein Fitnessarmband.“ stochastisch abhängig sind.

(3 BE)

100 Kunden des Unternehmens werden zufällig ausgewählt.

Berechne die Wahrscheinlichkeit dafür, dass mehr als $50\,\%$ der ausgewählten Kunden Datenschutzbedenken haben.

(2 BE)

Ersetzt man die Platzhalter $a$ und $b$ in geeigneter Weise, so kann mit dem Term

Term anzeigen

die Wahrscheinlichkeit eines Ereignisses im Sachzusammenhang berechnet werden.
Gib an, wodurch die Platzhalter zu ersetzen sind, und beschreibe das zugehörige Ereignis.

(3 BE)

Untersuche, ob es einen Wert von $n$ mit $n\gt0$ gibt, für den die folgende Aussage richtig ist:

Werden $2n$ Kunden des Unternehmens zufällig ausgewählt, so ist die Wahrscheinlichkeit dafür, dass unter diesen niemand Datenschutzbedenken hat, halb so groß wie bei $n$ Kunden.

(3 BE)

Ein Händler vermutet, dass die Fitnessarmbänder eines bestimmten Herstellers besonders häufig Fehler aufweisen. Um einen Anhaltspunkt für den Anteil der fehlerhaften Armbänder unter allen Fitnessarmbändern dieses Herstellers zu gewinnen, führt er einen Signifikanztest mit der Nullhypothese „Der Anteil der fehlerhaften Armbänder beträgt mindestens $7\,\%$ .“ durch.

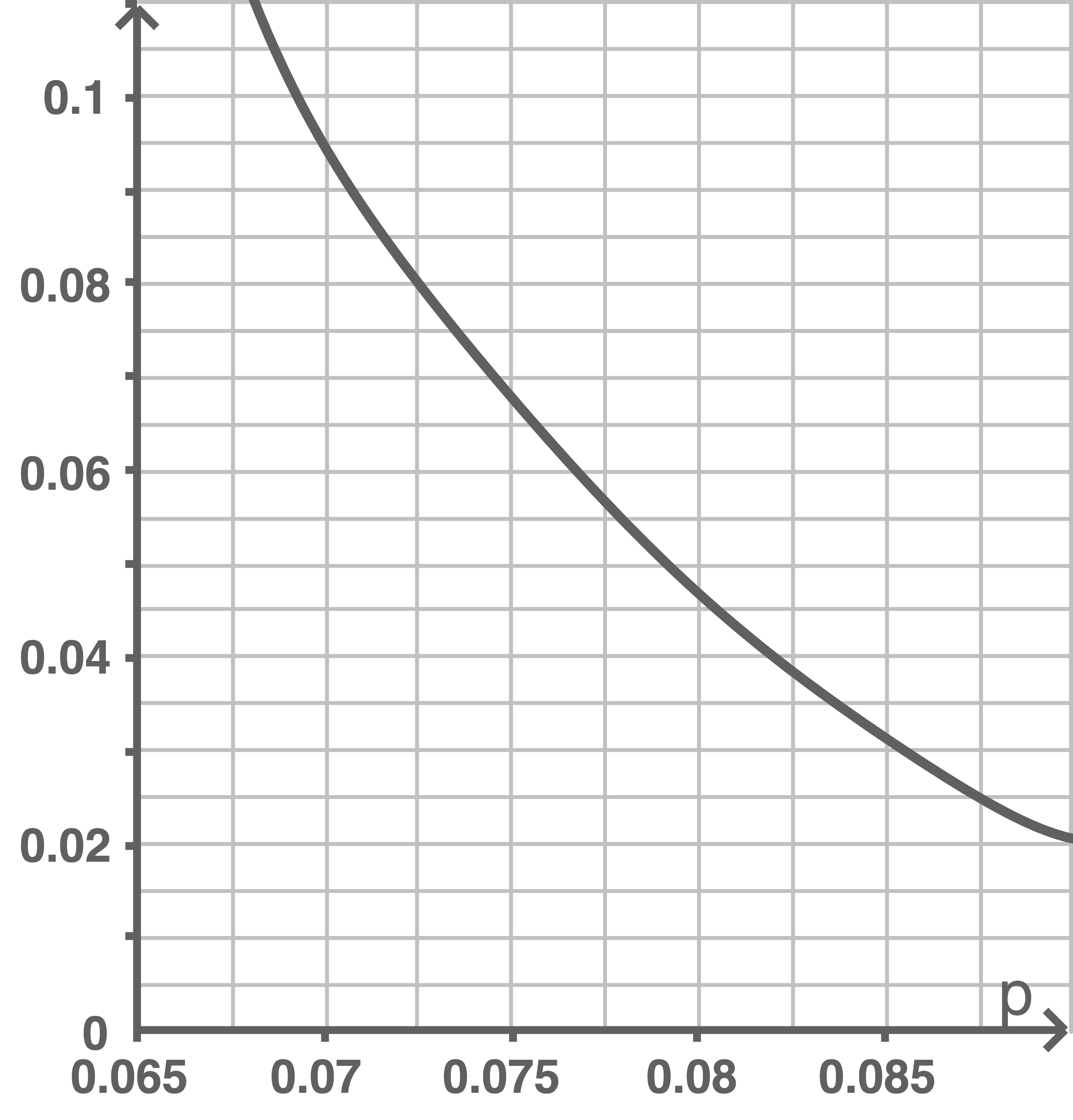
Für diesen Test gilt:

Die Nullhypothese wird abgelehnt, wenn höchstens vier Armbänder fehlerhaft sind.
Der Abbildung kann die Wahrscheinlichkeit für den Fehler erster Art in Abhängigkeit vom Anteil $p$ fehlerhafter Armbänder entnommen werden.

stochastik, signifikanzniveau, hypothesentest, wahrscheinlichkeit

Ermittle den Umfang der für den Test verwendeten Stichprobe.

(5 BE)

Gib an, welche Überlegung den Händler dazu veranlasst haben könnte, die gewählte Nullhypothese der Alternative „Der Anteil der fehlerhaften Armbänder beträgt höchstens $7\,\%$ .“ vorzuziehen. Begründe deine Angabe.

(3 BE)

Bei einer Werbeveranstaltung eines Elektrofachmarktes wird für die Kunden ein Gewinnspiel angeboten. Für einen Einsatz darf ein Kunde ein Glücksrad, das nur aus den Symbolen Sonne (S) oder Mond (M) besteht, siebenmal drehen. So entstehen Anordnungen aus sieben Symbolen. Die Wahrscheinlichkeit dafür, dass eine Sonne erscheint, ist $0,7$ , die für einen Mond $0,3$ .

Ermittle die Wahrscheinlichkeit dafür, dass die erzeugte Anordnung mit SSS endet.

(2 BE)

Interpretiere den folgenden Term im Sachzusammenhang $0,7^3\cdot \pmatrix{4\\2}\cdot 0,7^2\cdot 0,3^2$ .

(2 BE)

Eine Anordnung erzielt einen Gewinn (Einkaufsgutschein), wenn sie mehr als dreimal „Mond“ enthält.
Ermittle die Wahscheinlichkeit für den Erhalt eines Gewinns.

(2 BE)

Für Gewinne sind folgende Einkaufsgutscheine vorgesehen:

Anzahl der Monde	Einkaufsgutschein in Euro
4	2
5	10
6	100
7	1000

Je Gewinnspiel möchte der Elektronikfachmarkt durchschnittlich mindestens 20 Cent gewinnen. Ermittle den dafür nötigen Mindesteinsatz.

(4 BE)

Eine Anordnung mit genau zwei Sonnen an den vorderen fünf Stellen gewinnt einen Extrapreis. Ermittle die Wahrscheinlichkeit dafür, dass man mit einer Anordnung zugleich einen Gewinn und einen Extrapreis erhält.

(5 BE)

(40 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

baumdiagramm, wahrscheinlichkeiten berechnen, pfadregeln, fitnessarmband cas

D: Eine Person hat Datenschutzbedenken
F: Eine Person nutzt ein Fitnessarmband

Die Wahrscheinlichkeit $p,$ dass eine Person, die keine Datenschutzbedenken hat, ein Fitnessarmband benutzt, ergibt sich wie folgt:

$\begin{array}[t]{rll} 0,41\cdot p&=& 0,19 &\quad \scriptsize \mid\; : 0,41\\[5pt] p&\approx& 0,46 \end{array}$

$P_F(D)=\dfrac{P(D\cap F)}{P(F)}$ $=\dfrac{0,59\cdot 0,23}{0,59\cdot 0,23+0,19}\approx 0,42$

Die Wahrscheinlichkeit beträgt ungefähr $42\,\%.$

$0,23$ ist der Anteil an Kunden, die trotz Datenschutzbedenken ein Fitnessarmband nutzen.

$0,59\cdot 0,23+0,19$ ist der Anteil aller Kunden, die ein Fitnessarmband nutzen.

Da die beiden Anteile nicht gleich groß sind, sind die Ereignisse stochastisch abhängig.

Die Zufallsvariable $X$ beschreibt die Anzahl der Kunden mit Datenschutzbedenken. $X$ ist $B_{100;0,59}$ -verteilt.

$P(X\gt 50)=1-P(X\leq 50)$ $\approx 1-0,04=0,96$

Die Wahrscheinlichkeit beträgt ungefähr $96\,\%.$

$a=0,41\quad b=49$

Der Term beschreibt das Ereignis, dass höchstens die Hälfte aller ausgewählten Kunden Datenschutzbedenken hat.

Die Wahrscheinlichkeit, dass unter $2n$ zufällig ausgewählten Kunden niemand Datenschutzbedenken hat, ist gegeben durch $0,41^{2n}.$
Die Wahrscheinlichkeit, dass bei $n$ zufällig ausgewählten Kunden niemand Datenschutzbedenken hat, beträgt $0,41^n.$

Es soll gelten:

$\begin{array}[t]{rll} 0,41^{2n} &=& \dfrac{1}{2}\cdot0,41^n \quad \scriptsize \mid\; :0,41^n \\[5pt] 0,41^n&=&\dfrac{1}{2} \end{array}$

Die Gleichung gilt für kein $n \in \mathbb N$ . Somit gibt es keinen Wert für $n,$ für den die Aussage richtig ist.

Der Abbildung kann entnommen werden, dass die Wahrscheinlichkeit für einen Fehler erster Art bei $p=0,07$ ungefähr bei $0,097$ liegt.

Die Zufallsvariable $Y$ beschreibt die Anzahl der fehlerhaften Armbänder. $Y$ ist $B_{n;0,07}$ -verteilt, wobei der Parameter $n$ gesucht ist.

Die Nullhypothese wird abgelehnt, wenn höchstens vier Armbänder fehlerhaft sind. Gesucht ist also ein Wert für $n,$ sodass $P(Y\leq 4)\approx 0,097$ gilt.

Systematisches Ausprobieren mit dem Taschenrechner liefert:

$n=112: P(Y\leq 4)\approx 0,101$
$n=113: P(Y\leq 4)\approx 0,097$
$n=114: P(Y\leq 4)\approx 0,093$

Die Stichprobe für den Test hatte einen Umfang von $113$ Armbändern.

Bei der gewählten Nullhypothese beträgt das Risiko, fälschlicherweise von einem zu geringen Anteil fehlerhafter Armbänder auszugehen, höchstens $9,7\,\%$ und ist somit gering. Die Wahrscheinlichkeit, fälschlicherweise von einem zu großen Anteil fehlerhafter Armbänder auszugehen, kann dagegen deutlich größer sein.

$P(\text{SSS})=0,7^3=0,343$

Die Wahrscheinlichkeit beträgt $34,3\,\%.$

Der Term gibt bespielsweise die Wahrscheinlichkeit dafür an, dass die ersten drei Stellen der Anordnung Sonnen sind und bei den restlichen vier Stellen genau zwei Monde dabei sind.

Die Zufallsvariable $Z$ beschreibt die Anzahl der Monde in der Anordnung. $Z$ ist $B_{7;0,3}$ -verteilt.

$P(Z\geq 4)=1-P(Z\leq 3)$ $\approx1-0,874=0,126$

Die Wahrscheinlichkeit für den Erhalt eines Gewinnes beträgt ungefähr $12,6\,\%.$

Der Parameter $a$ gibt den nötigen Mindesteinsatz an.

In der folgenden Tabelle sind die Gewinne bzw. Verluste $z_i$ für den Elektrofachmarkt bei einem Einsatz $a$ mit ihrer jeweiligen Wahrscheinlichkeit gegeben:

$z_i$	$P(Z=z_i)$
$a-2$	$P(Z=4)$ $=0,0972$
$a-10$	$P(Z=5)$ $=0,025$
$a-100$	$P(Z=6)$ $=0,0036$
$a-1000$	$P(Z=7)$ $=0,0002$
$a$	$P(Z\leq 3)$ $=0,874$

Der erwartete Gewinn in Abhängigkeit von $a$ lässt sich wie folgt berechnen:

$E(Z)=(a-2)\cdot0,0972$ $+(a-10)\cdot 0,025$ $+(a-100)\cdot 0,0036$ $+(a-1000)\cdot0,0002$ $+a\cdot0,874$ $= a-1,0044$

Es soll $E(Z)\geq 0,2$ gelten:

$\begin{array}[t]{rll} a-1,0044 &\geq& 0,2 \quad \scriptsize \mid\;+1,0044 \\[5pt] a &=& 1,2044 \end{array}$

Der nötige Mindesteinsatz beträgt also $1,21\,€.$

$G:$ Es wird ein Gewinn erzielt
$E:$ Es wird ein Extrapreis erzielt

Die Zufallsvariable $W$ beschreibt die Anzahl der Sonnen. $W$ ist $B_{5;0,7}$ -verteilt.

$P(W=2)=0,1323$

Damit zugleich ein Gewinn und ein Extrapreis erzielt wird, muss die Anordnung genau zwei Sonnen an den vorderen fünf Stellen haben und mindestens viermal den Mond enthalten. Unter den letzten beiden Symbolen darf die Sonne also höchstens einmal vorkommen.

$P(E\cap G)$ $=0,1323\cdot 0,3^2+0,1312\cdot 2\cdot 0,7\cdot 0,3$ $\approx0,06747$

Die gesuchte Wahrscheinlichkeit beträgt ungefähr $6,75\,\%.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?