Stochastik 3.2 - Stahlkugeln

Stochastik: Stahlkugeln

Ein Unternehmen produziert Stahlkugeln für Kugellager. Erfahrungsgemäß sind $4 \,\%$ aller Kugeln fehlerhaft.
$800$ Kugeln werden zufällig ausgewählt. Die Anzahl der fehlerhaften Kugeln unter den ausgewählten kann durch eine binomialverteilte Zufallsgröße $X$ beschrieben werden.

Bestimme die Wahrscheinlichkeit für die folgenden Ereignisse.

$C:$

„Genau $30$ der ausgewählten Kugeln sind fehlerhaft. “

$D:$

„Weniger als $30$ der ausgewählten Kugeln sind fehlerhaft. “

(3 BE)

Es gilt: $P(X=35) \approx 6\,\%.$
Interpretiere diese Aussage im Sachzusammenhang.

(2 BE)

Bestimme die Wahrscheinlichkeit dafür, dass die Anzahl der fehlerhaften Kugeln unter den ausgewählten höchstens um eine halbe Standardabweichung vom Erwartungswert dieser Anzahl abweicht.

(5 BE)

Eine fehlerhafte Kugel hat entweder einen Formfehler oder einen Größenfehler. Die Wahrscheinlichkeit dafür, dass eine Kugel einen Formfehler hat, beträgt $3\,\%$ . Alle Kugeln werden vor dem Verpacken geprüft. Dabei werden $95 \,\%$ der Kugeln mit Formfehler, $98 \,\%$ der Kugeln mit Größenfehler, aber auch $0,5 \,\%$ der Kugeln ohne Fehler aussortiert.

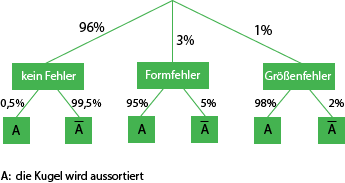
Stelle den Sachzusammenhang in einem beschrifteten Baumdiagramm dar.

(4 BE)

Beurteile unter Zuhilfenahme geeigneter Rechnungen folgende Aussage:

Die Wahrscheinlichkeit, dass eine Kugel nicht aussortiert wird, ist doppelt so groß wie die Wahrscheinlichkeit, dass eine aussortierte Kugel keinen Formfehler hat.

(6 BE)

Aufgrund zunehmender Reklamationen wird vermutet, dass der Anteil der fehlerhaften Kugeln auf über $4 \,\%$ angestiegen ist. Um diese Vermutung zu prüfen, soll die Nullhypothese „Der Anteil der fehlerhaften Kugeln beträgt höchstens $4\,\%$ .“ auf der Grundlage einer Stichprobe von $500$ Kugeln getestet werden.
Wenn das Ergebnis des Tests die Vermutung nicht entkräftet, soll die Produktion unterbrochen werden, um die Maschinen zu warten. Das Risiko, die Produktion irrtümlich zu unterbrechen, soll höchstens $3 \,\%$ betragen.

Beschreibe für diesen Test im Sachzusammenhang den Fehler zweiter Art.
Gib die Konsequenz an, die sich aus diesem Fehler für die Produktion ergeben würde.

(3 BE)

Für den beschriebenen Test wird der Ablehnungsbereich betrachtet. Eine der beiden Grenzen dieses Ablehnungsbereichs ist größer als $0$ und kleiner als $500$ ; diese Grenze wird mit $k$ bezeichnet. Zur Bestimmung des Werts von $k$ soll die binomialverteilte Zufallsgröße $Y$ mit den Parametern $n= 500$ und $p= 0,04$ verwendet werden.
Begründe, dass keine der beiden Ungleichungen I und II den korrekten Wert von $k$ liefert.

$P(Y\leq k) \leq 0,03$

$P(Y\leq k) \gt 0,97$

(4 BE)

Die Kugeln werden in Packungen verkauft. Ein Teil der verkauften Packungen wird zurückgegeben. Die Wahrscheinlichkeit dafür, dass eine verkaufte Packung zurückgegeben wird, beträgt $3 \,\%$ . Dem Unternehmen entsteht pro Packung, die zurückgegeben wird, ein Verlust von $5,80$ Euro; pro Packung, die nicht zurückgegeben wird, erzielt das Unternehmen einen Gewinn von $8,30$ Euro.
Bestimme die Wahrscheinlichkeit, mit der das Unternehmen bei einem Verkauf von $200$ Packungen einen Gesamtgewinn von mindestens $1500$ Euro erzielt.

(4 BE)

In einer Packung von $20$ Kugeln sind genau $2$ fehlerhafte Kugeln.

Es werden zufällig nacheinander drei Kugeln aus der Packung entnommen, ohne sie zurückzulegen.
Ermittle die Wahrscheinlichkeit für die folgenden Ereignisse:

$F:$

„Die dritte Kugel ist fehlerhaft. “

$G:$

„Mindestens eine Kugel ist fehlerhaft. “

(5 BE)

Es sollen $k$ Kugeln aus der Packung entnommen werden, ohne sie zurückzulegen. Dabei soll die Wahrscheinlichkeit $p$ dafür, dass mindestens eine der entnommenen Kugeln eine fehlerhafte Kugel ist, kleiner als 0,5 sein.
Ermittle, wie viele Kugeln höchstens entnommen werden dürfen, wenn die Bedingung „p kleiner als 0,5 “ erfüllt bleiben soll.

(4 BE)

(40 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

$X$ ist binominalverteilt und gibt die Anzahl an fehlterhaften Kugeln an.
$n=800$ und $p=0,04.$

$P(C)=P(X=30)=0,069=6,9\,\%$

$\blacktriangleright$ TI nspire CAS

menu $\to$ 5 $\to$ 5 $\to$ E: Binomial Cdf

$\blacktriangleright$ Casio Classpad II

Interaktiv $\to$ Verteilungsfunktionen $\to$ Diskret $\to$ binomial CDf

$P(D)=P(X\leq 29)=0,334=33,4\,\%$

$P(X=35)=6\,\%$ ist die Wahrscheinlichkeit, dass von 800 zufällig ausgewählten Kugeln exakt 35 fehlerhaft sind.

Der Erwartungswert beträgt:

$E=p\cdot n=0,04\cdot800=32$

Die Standartabweichung beträgt:

$\sigma=\sqrt{n\cdot p\cdot (1-p)}$ $=\sqrt{800\cdot0,04\cdot 0,96}$ $=5,54$

$32-\dfrac{\sigma}{2}\approx29\quad 32+\dfrac{\sigma}{2}\approx35$

$P(29\leq X\leq35)$ $=P(X\leq35)-P(X\leq29)$ $=0,407=40,7\,\%$

Diagramm zur Fehleranalyse mit Wahrscheinlichkeiten für verschiedene Fehlerarten.

$P(E)$ ist die Wahrscheinlichkeit an, dass eine Kugel nicht aussortiert wird.

Vollständigen Rechenweg anzeigen

$P(F)$ ist die Wahrscheinlichkeit, dass eine aussortierte Kugel keinen Formfehler hat. Um diese zu berechnen wird der Satz von Bayes verwendet:

$P(A\mid B)= \dfrac{P(B\mid A)\cdot P(A)}{P(B)}$

Vollständigen Rechenweg anzeigen

Somit ist $P(E)$ nicht doppelt so groß wie $P(F).$

Ein Fehler zweiter Art liegt vor, wenn die Nullhypothese nicht zutrifft, aber fälschlicherweise durch die Stichprobe bestätigt wird. Das Unternehmen geht also davon aus, dass Nullhypothese korrekt ist und die Maschine mit einem Fehleranteil von nicht mehr als $4\%$ produziert. Tatsächlich aber hat die Maschine einen höheren Fehleranteil und müsste gewartet werden.

Das Risiko, die Produktion irrtümlich zu unterbrechen, soll höchstens $3\%$ betragen. Das heißt: Die Wahrscheinlichkeit, dass die Anzahl der fehlerhaften Kugeln mindestens $k$ beträgt soll höchstens $3\%$ sein. Das wiederum bedeutet, dass die Wahrscheinlichkeit, dass es weniger als $k$ fehlerhafte Kugeln gibt größer als $97\%$ ist.

$Y$ ist binominalverteilt und gibt die Anzahl der zurückgegebenen Packungen an.
$n=200\quad p=0,03$

$y\cdot5,8+(1-y)\cdot8,3\geq 1500$
$14,2y \leq 160$
$y\leq11$

$\blacktriangleright$ TI nspire CAS

menu $\to$ 5 $\to$ 5 $\to$ E: Binomial Cdf

$\blacktriangleright$ Casio Classpad II

Interaktiv $\to$ Verteilungsfunktionen $\to$ Diskret $\to$ binomial CDf

$P(Y\leq11)=0,982=98,2\%$

Für $P(F)$ gilt: Die dritte Kugel ist fehlerhaft. Eine der ersten beiden Kugeln ist fehlerhaft oder keine der ersten beiden Kugeln ist fehlerhaft:

Vollständigen Rechenweg anzeigen

Um $P(G)$ zu bestimmen, kann die Gegenwahrscheinlichkeit (keine Kugel ist fehlerhaft) genutzt werden:

$P(G)=1-\dfrac{18}{20}\cdot\dfrac{17}{19}\cdot\dfrac{16}{18}=\dfrac{27}{95}$ $=28,4\%$

Es wird die Wahrscheinlichkeit für verschiedene Werte von $k$ berechnet. Dabei wird wieder die Gegenwahscheinlichkeit (keine Kugel ist fehlerhaft) zur Hilfe genommen:

Für $k=5$ gilt $P(G)=1-\dfrac{18}{20}\cdot\dfrac{17}{19}\cdot\dfrac{16}{18}\cdot\dfrac{15}{17}\cdot\dfrac{14}{16}$ $=0,368\lt0,05$

Für $k=6$ gilt

Vollständigen Rechenweg anzeigen

Somit dürfen maximal 5 Kugeln entfernt werden, damit die Bedingung erfüllt bleibt.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?