Analysis 2.2 - Flugzeugflügel
Analysis: Flugzeugflügel
Gegeben ist die in
a)
Berechne die Nullstellen der Funktion  in Abhängigkeit von
in Abhängigkeit von 
(2 BE)
b)
Gib das Verhalten der Funktionswerte von  für
für  und
und  an.
an.
(2 BE)
c)
Ermittle die Art und die Lage der lokalen Extrempunkte von  .
(zur Kontrolle:
.
(zur Kontrolle:  )
)
(5 BE)
d)
Bestimme eine Gleichung der Kurve, auf der die Hochpunkte der Graphen  liegen.
liegen.
(2 BE)
e)
Für die Stelle  der Funktion
der Funktion  gelten folgende Bedingungen:
gelten folgende Bedingungen:
 an.
an.
Weiterhin wird die in
(1 BE)
f)
Die Graphen  und
und  schneiden sich in den Punkten
schneiden sich in den Punkten  und
und 
Entscheide, welcher dieser Punkte Schnittpunkt aller Graphen mit
mit  ist.
ist.
Begründe deine Entscheidung.
Entscheide, welcher dieser Punkte Schnittpunkt aller Graphen
Begründe deine Entscheidung.
(2 BE)
g)
Die Funktion  besitzt folgende Eigenschaften:
besitzt folgende Eigenschaften:
 einen Wendepunkt besitzt.
einen Wendepunkt besitzt.
(3 BE)
h)
Der Graph einer Funktion  geht aus dem Graphen
geht aus dem Graphen  hervor. Es gilt:
hervor. Es gilt:
 an.
an.
- der Graph
wurde an beiden Koordinatenachsen gespiegelt und
- der gespiegelte Graph
wurde danach so verschoben, dass gilt:
(3 BE)
i)
An den Graphen  wird im Schnittpunkt mit der
wird im Schnittpunkt mit der  -Achse eine Tangente
-Achse eine Tangente  gelegt.
gelegt.
Die Tangente schließt mit der
schließt mit der  -Achse und der Geraden
-Achse und der Geraden  mit
mit 
 eine Fläche von
eine Fläche von  ein.
ein.
Bestimme .
(zur Kontrolle:
.
(zur Kontrolle:  )
)
Die Tangente
Bestimme
(3 BE)
j)
Die Tangente  aus der Teilaufgabe
aus der Teilaufgabe  , die
, die  -Achse und die Gerade
-Achse und die Gerade  mit
mit  begrenzen vollständig eine Fläche
begrenzen vollständig eine Fläche  .
Ermittle das Teilverhältnis der Strecken
.
Ermittle das Teilverhältnis der Strecken  wenn gilt:
wenn gilt:
 und
und 
Die Konstrukteure einer kleinen Firma haben einen neuartigen Flugzeugflügel entworfen. Dabei werden die Graphen der Funktionen
(3 BE)
Es gilt:
k)
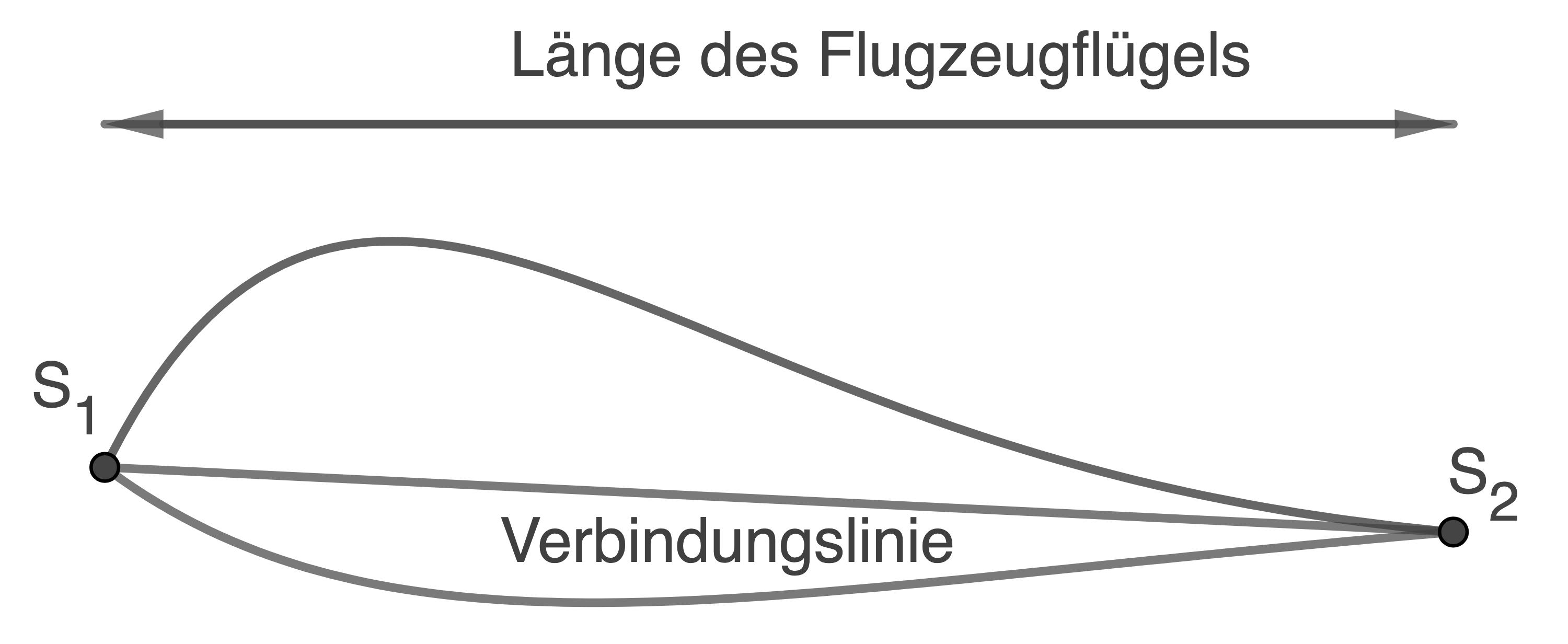
Für die Konstruktion des Flugzeugflügels müssen folgende Bedingungen erfüllt sein:
(I)
Die Länge des Flugzeugflügels ist der horizontale Abstand zwischen  und
und  Diese Länge beträgt
Diese Länge beträgt 
(II)
Die maximale vertikale Höhe des Flugzeugflügels lässt sich mithilfe der Differenzfunktion von  und
und  bestimmen. Sie darf
bestimmen. Sie darf  nicht überschreiten.
nicht überschreiten.
(III)
Der Neigungswinkel zwischen Verbindungslinie  und der Horizontalen soll kleiner als
und der Horizontalen soll kleiner als  sein.
sein.
Prüfe, ob diese Bedingungen eingehalten wurden.
(8 BE)
l)
Begründe ohne Rechnung, dass die Länge des Flugzeugflügels kürzer als die Verbindungslinie zwischen  und
und  ist.
ist.
(2 BE)
m)
Die Richtung, aus der während einer bestimmten Phase des Fluges die Luft anströmt, kann modellhaft durch eine Gerade zwischen  und einem Punkt
und einem Punkt  mit
mit  angenommen werden. Im Punkt
angenommen werden. Im Punkt  ändert der Graph von
ändert der Graph von  seine Krümmungsart.
seine Krümmungsart.
Weise nach, dass die Größe des Winkels nicht mehr als
nicht mehr als  beträgt.
beträgt.
Weise nach, dass die Größe des Winkels
(5 BE)
n)
In den Flugzeugflügel soll ein quaderförmiger Tank integriert werden. Die Querschnittsfläche des Tanks kann durch ein achsenparalleles Rechteck, dessen untere Seite auf der  -Achse liegt, modelliert werden. Dieser Tank hat im Querschnitt die Maße
-Achse liegt, modelliert werden. Dieser Tank hat im Querschnitt die Maße  .
.
Stelle diesen Sachverhalt in einer Skizze dar. Zeige rechnerisch, dass ein solcher Tank nicht in den Flugzeugflügel eingebaut werden kann.
Stelle diesen Sachverhalt in einer Skizze dar. Zeige rechnerisch, dass ein solcher Tank nicht in den Flugzeugflügel eingebaut werden kann.
(4 BE)
o)
Vereinfachend kann angenommen werden, dass ein Teil eines Flugzeugflügels stets den abgebildeten Querschnitt und eine Tiefe von  besitzt.
besitzt.
Ein moderner Flugzeugflügel besteht zu ca. aus carbonfaserverstärktem Kunststoff (CFK). CFK hat neben einer besseren Stabilität vor allem den Vorteil der Massereduktion durch eine geringere Dichte (ca.
aus carbonfaserverstärktem Kunststoff (CFK). CFK hat neben einer besseren Stabilität vor allem den Vorteil der Massereduktion durch eine geringere Dichte (ca.  ) als herkömmliche Stoffe wie Aluminium (ca.
) als herkömmliche Stoffe wie Aluminium (ca.  ).
).
Bestimme für den beschriebenen Teil des Flugzeugflügels die benötigte Masse an CFK in und die Massereduktion gegenüber der bisherigen Verwendung von Aluminium in
und die Massereduktion gegenüber der bisherigen Verwendung von Aluminium in 
Ein moderner Flugzeugflügel besteht zu ca.
Bestimme für den beschriebenen Teil des Flugzeugflügels die benötigte Masse an CFK in
(5 BE)
(50 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?Flugzeugflügel
a)
b)
c)
Mit der Produktregel wird zunächst die Ableitung von  gebildet:
gebildet:

 kann nicht null werden.
kann nicht null werden.



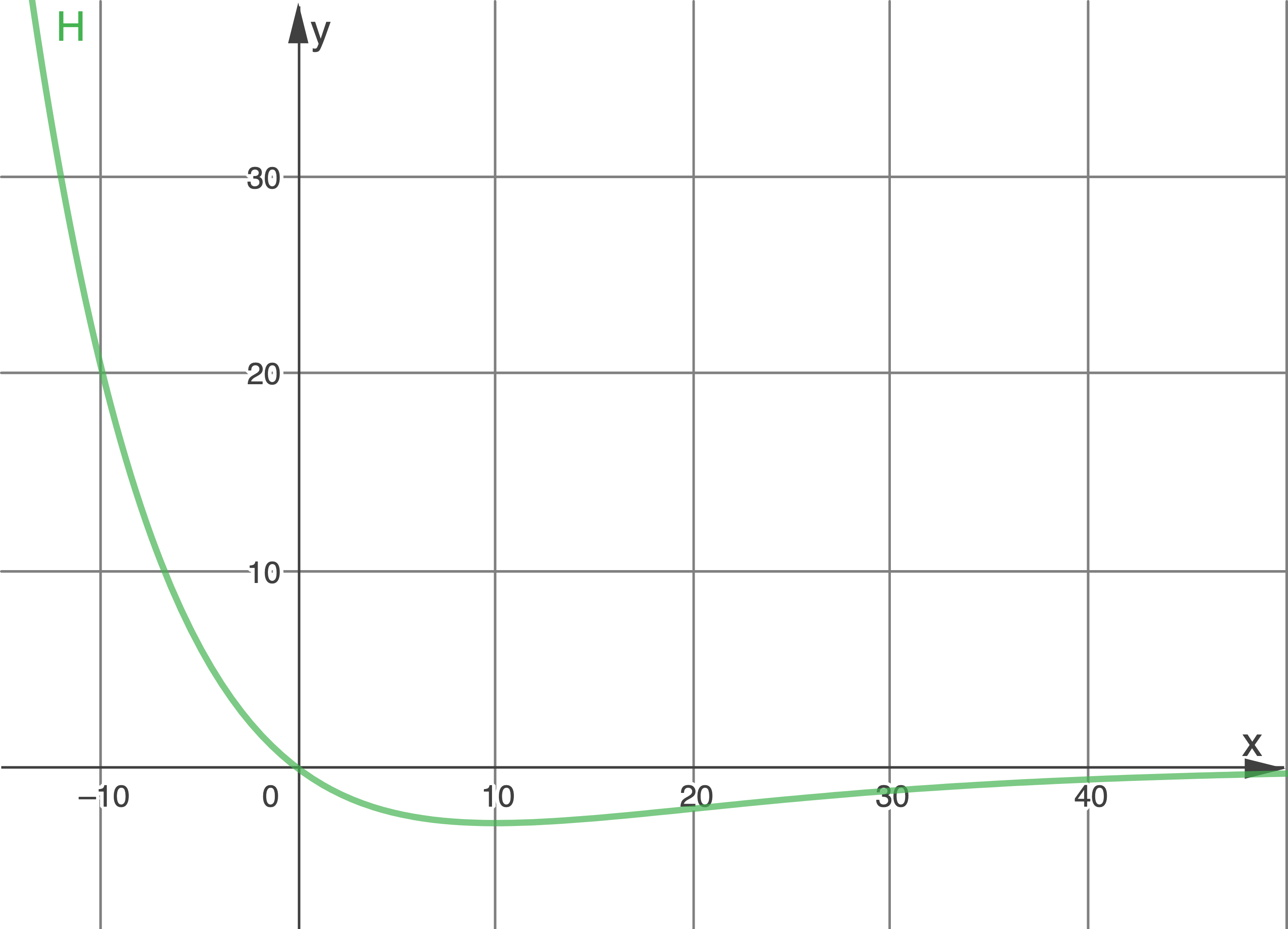
 Am Schaubild ist zu sehen, dass bei
Am Schaubild ist zu sehen, dass bei  einen Tiefpunkt und bei
einen Tiefpunkt und bei  einen Hochpunkt gibt.
einen Hochpunkt gibt.
d)
Zunächst muss der Hochpunkt von  bestimmt werden:
bestimmt werden: 
 Auf
Auf  auflösen:
auflösen:
 Nun wird der
Nun wird der  -Wert berechnet:
-Wert berechnet:
 Um die Gleichung der Ortskurve zu erhalten, muss nun
Um die Gleichung der Ortskurve zu erhalten, muss nun  in
in  eingesetzt werden:
eingesetzt werden:

e)
An der Stelle  ist die Ableitung zweiten Grades gleich null und die Ableitung dritten Grades ungleich null. Somit befindet sich am Graph an dieser Stelle ein Wendepunkt.
ist die Ableitung zweiten Grades gleich null und die Ableitung dritten Grades ungleich null. Somit befindet sich am Graph an dieser Stelle ein Wendepunkt.
f)
Der Punkt  ist Schnittpunkt aller Graphen der Funktion
ist Schnittpunkt aller Graphen der Funktion  mit dem Graph
mit dem Graph  . Es gilt:
. Es gilt:
 unabhängig von
unabhängig von 
g)
h)
Zunächst wird der Graph an der  -Achse gespiegelt:
-Achse gespiegelt:
 Nun zusätzlich an der
Nun zusätzlich an der  -Achse:
-Achse:
 Damit
Damit  gilt, muss der gespiegelte Graph um eine Längeneinheit nach oben verschoben werden:
gilt, muss der gespiegelte Graph um eine Längeneinheit nach oben verschoben werden:

i)
j)
k)
Bedingung 1:
Aus Aufgabe f können die Schnitstellen und
und  entnommen werden.
entnommen werden.
![\(\dfrac{55}{2}-0=27,5\;\text{[dm]}\)](https://mathjax.schullv.de/c39fba025287db015b40df2a8148199f2c8966d3d6cbd4e88c84efda1b6997c9?color=5a5a5a)
Bedingung 1 ist somit erfüllt. Bedingung 2:
Es müssen die Koordinaten des Hochpunkts der Differenzfunktion bestimmt werden.
bestimmt werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 Der Flügel hat eine maximale vertikale Höhe von
Der Flügel hat eine maximale vertikale Höhe von 
Somit ist Bedingung 2 ebenfalls erfüllt. Bedingung 3:

 Somit ist auch Bedingung 3 erfüllt.
Somit ist auch Bedingung 3 erfüllt.
Aus Aufgabe f können die Schnitstellen
Bedingung 1 ist somit erfüllt. Bedingung 2:
Es müssen die Koordinaten des Hochpunkts der Differenzfunktion
menu  6: Graph analysieren
6: Graph analysieren  3: Maximum
3: Maximum
Analyse  Grafische Lösung
Grafische Lösung  Maximum
Maximum
Somit ist Bedingung 2 ebenfalls erfüllt. Bedingung 3:
l)
Die Verbindungsstrecke der beiden Punkte ist länger, da sie sich sowohl in  -Richtung, als auch in
-Richtung, als auch in  -Richtung erstreckt. Die Verbindsungslinie entspricht der Hypotenuse in einem rechtwinkligen Dreieck. Die Hypotenuse ist immer die längste Strecke im Dreieck.
-Richtung erstreckt. Die Verbindsungslinie entspricht der Hypotenuse in einem rechtwinkligen Dreieck. Die Hypotenuse ist immer die längste Strecke im Dreieck.
m)
Gesucht wird nach dem Wendepunkt. Dieser kann durch die Nullstelle der zweiten Ableitung von  bestimmt werden.
bestimmt werden.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Im Bereich
Casio Classpad II
Im Bereich  existiert folgender Wendepunkt:
existiert folgender Wendepunkt:
 Um den Winkel
Um den Winkel  zu berechnen, müssen der Neigungswinkel
zu berechnen, müssen der Neigungswinkel  der Strecke
der Strecke  und der Neigungswinkel
und der Neigungswinkel  des Punktes
des Punktes  addiert werden:
addiert werden:



menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

n)
Zunächst werden die Koordinaten der Schnittpunkte des Graphen der Funktion  mit einer Geraden
mit einer Geraden  bestimmt:
bestimmt:
 Nun wird die Länge der Strecke
Nun wird die Länge der Strecke  bestimmt:
bestimmt:
 Ein
Ein 
 breites Rechteck passt somit nicht in die Querschnittsfläche des Flügels.
breites Rechteck passt somit nicht in die Querschnittsfläche des Flügels.
o)
Zunächst wird der Flächeninhalt der Querschnittsfläche des Flügels bestimmt. Dazu wird die Differenzfunktion  aus Teilaufgabe k) integriert. Als Grenzen werden die Schnittstellen der Funktionen
aus Teilaufgabe k) integriert. Als Grenzen werden die Schnittstellen der Funktionen  und
und  verwendet.
verwendet.
![\(A=\displaystyle\int_{0}^{27,5}d(x)\;\mathrm dx=105,37\;\text{[dm]}^2\)](https://mathjax.schullv.de/d79f266c2706ee6fd47012f04de98f428d7ed829df0da170f8af189f9f76a302?color=5a5a5a) Nun wird das Volumen berechnet:
Nun wird das Volumen berechnet:
![\(V_{ges}= 105,37\;\text{[dm]}^2\cdot20\;\text{[dm]}\)](https://mathjax.schullv.de/55052bd8f006ac006c597088180e4b0f3ee2d7ccca4dcc9b1508baa85b721063?color=5a5a5a)
![\(=2107,4\;\text{[dm]}^3\)](https://mathjax.schullv.de/8256d9b8f36c04a7ae53e02ea9cfd1067269835a85f4c81b9d8d8f142fd6c62f?color=5a5a5a) Das CFK-Volumen beträgt:
Das CFK-Volumen beträgt:
![\(V_{CFK}=2107,4\;\text{[dm]}^3\cdot0,53\)](https://mathjax.schullv.de/415906b2bca4d51b202d7a06add461d9c713afda5d039dd61c75c04fe3030f17?color=5a5a5a)
![\(=1116,92\;\text{[dm]}^3\)](https://mathjax.schullv.de/74395b49d9071a342743692d97112080331a0d0b496e0879045662bd9884f5f7?color=5a5a5a) Zuletzt wird die Masse berechnet:
Zuletzt wird die Masse berechnet:

 Somit werden
Somit werden  CFK benötigt.
CFK benötigt.