Analysis 2.1 - Exponentialfunktionen
Gegeben ist die Schar der in  definierten Funktionen
definierten Funktionen  mit
mit 
 Die Graphen von
Die Graphen von  werden mit
werden mit  bezeichnet.
bezeichnet.
 definierten Funktionen
definierten Funktionen  mit
mit 

a)
Gib das Verhalten der Funktionswerte von  für
für  in Abhängigkeit von
in Abhängigkeit von  an.
an.
(3 BE)
b)
Ermittle die Anzahl der Nullstellen von  in Abhängigkeit von
in Abhängigkeit von 
(4 BE)
c)
Die Abbildung stellt die Graphen  und
und  dar. Ordne den Graphen I und II ihren jeweiligen Parameter zu.
dar. Ordne den Graphen I und II ihren jeweiligen Parameter zu.
Skaliere die Koordinatenachsen.
Gib den gemeinsamen Schnittpunkt aller Graphen mit der
mit der  -Achse an.
-Achse an.
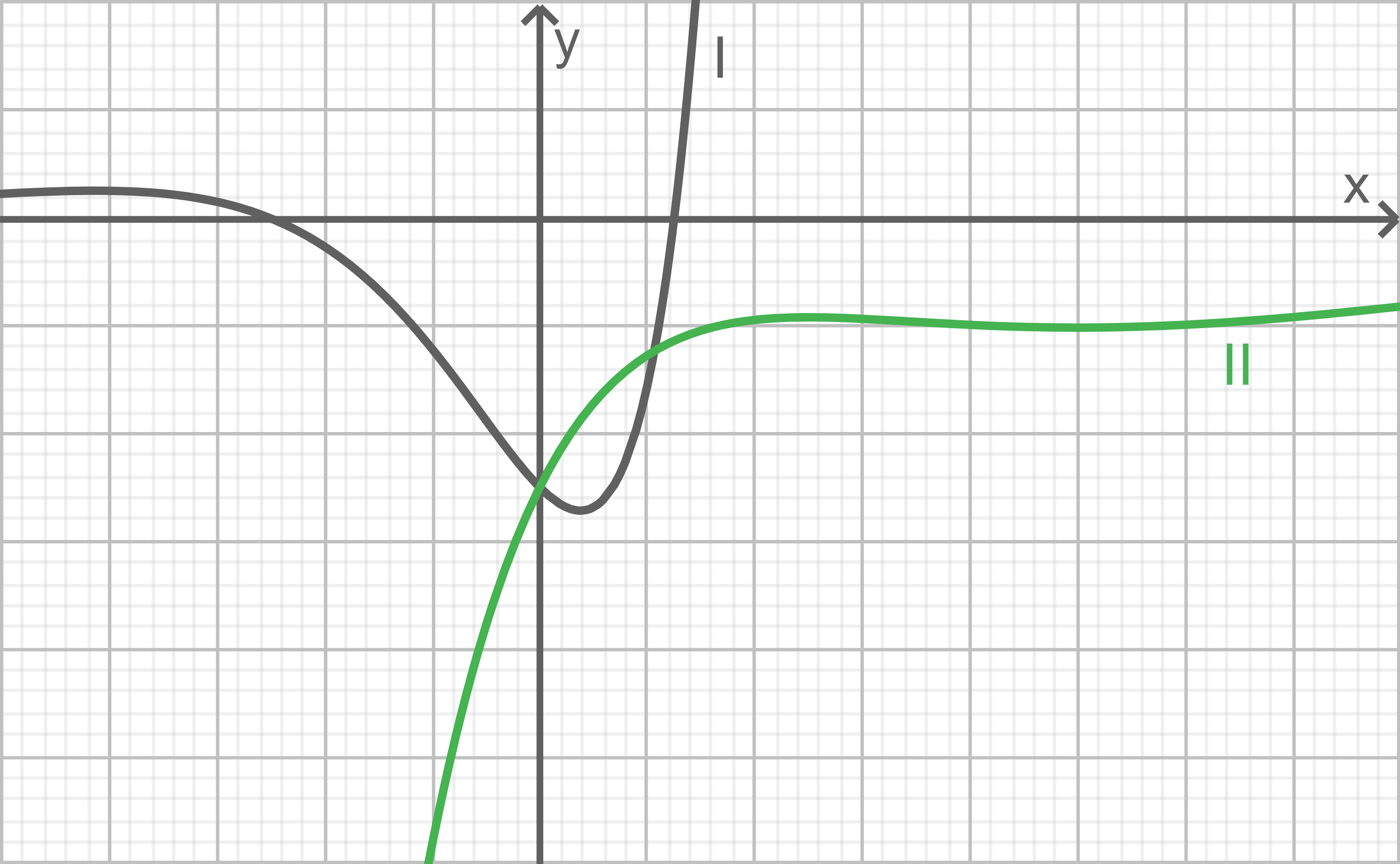
Skaliere die Koordinatenachsen.
Gib den gemeinsamen Schnittpunkt aller Graphen

(3 BE)
d)
Zeige, dass  und
und  mögliche lokale Extremstellen von
mögliche lokale Extremstellen von  sind.
sind.
(2 BE)
e)
Die Gerade durch die beiden einzigen lokalen Extrempunkte von  schneidet die
schneidet die  -Achse im Punkt
-Achse im Punkt 
Bestimme die Koordinaten von näherungsweise.
näherungsweise.
Bestimme die Koordinaten von
(zur Kontrolle:  )
)
(3 BE)
f)
Durch Spiegelung der Graphen von  an der
an der  -Achse entstehen die Graphen einer Funktionsschar
-Achse entstehen die Graphen einer Funktionsschar 
Es gibt zwei Werte für so dass gilt:
so dass gilt:
Die Tangente an den Graphen von an der Stelle
an der Stelle  die Tangente an den Graphen von
die Tangente an den Graphen von  an der Stelle
an der Stelle  und die
und die  -Achse begrenzen ein Dreieck, das gleichseitig ist. Bestimme diese beiden Werte von
-Achse begrenzen ein Dreieck, das gleichseitig ist. Bestimme diese beiden Werte von 
Gegeben ist zusätzlich die Schar der in Es gibt zwei Werte für
Die Tangente an den Graphen von
(4 BE)
g)
Im Zusammenhang mit  wurde folgende Rechnung durchgeführt:
wurde folgende Rechnung durchgeführt:
(5 BE)
h)
Die Punkte  und der Schnittpunkt des Graphen von
und der Schnittpunkt des Graphen von  mit der
mit der  -Achse sind Eckpunkte eines Dreiecks. Bestimme die Innenwinkel des Dreiecks.
-Achse sind Eckpunkte eines Dreiecks. Bestimme die Innenwinkel des Dreiecks.
(4 BE)
i)
Beschreibe ein Verfahren zur Berechnung des Flächeninhalts des Dreiecks aus Teilaufgabe h.
(3 BE)
j)
Bestimme den Wert für  für den der Graph von
für den der Graph von  die
die  -Achse im Winkel von
-Achse im Winkel von  schneidet.
schneidet.
(2 BE)
k)
Begründe die folgende Aussage:

Aus der Lage und Art der Extrempunkte der Graphen der Funktionenschar  lässt sich schlussfolgern, dass keine Funktion der Schar
lässt sich schlussfolgern, dass keine Funktion der Schar  eine Nullstelle besitzt.
eine Nullstelle besitzt.
(3 BE)
l)
Weise nach, dass gilt 
(1 BE)
m)
Betrachtet wird der Inhalt der Fläche, den der Graph II (siehe Abbildung) mit der  -Achse im selben Intervall wie in Teilaufgabe l begrenzt.
-Achse im selben Intervall wie in Teilaufgabe l begrenzt.
Beurteile mithilfe der Abbildung, ob der Inhalt dieser Fläche größer oder kleiner als der in Teilaufgabe l berechnete Wert ist.
Beurteile mithilfe der Abbildung, ob der Inhalt dieser Fläche größer oder kleiner als der in Teilaufgabe l berechnete Wert ist.
(3 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
1. Fall: 
![\(\begin{array}[t]{rll}
\lim\limits_{x\to+\infty}f_a(x)&=&\lim\limits_{x\to+\infty}((x-5) \cdot 1) \\[5pt]
&=&+\infty
\end{array}\)](https://mathjax.schullv.de/bdd9eb8498f9a7c62ae4f0ad4250f996d4d25930e129dd253fcc13412a4c89cd?color=5a5a5a) 2. Fall:
2. Fall:  3. Fall:
3. Fall:  Da für
Da für  der Term
der Term  schneller steigt bzw. fällt als
schneller steigt bzw. fällt als  geht der erste Faktor von
geht der erste Faktor von  gegen
gegen  Der zweite Faktor
Der zweite Faktor  geht in diesem Fall für
geht in diesem Fall für  gegen
gegen  Da die
Da die  -Funktion schneller steigt bzw. fällt als der erste Faktor, folgt somit
-Funktion schneller steigt bzw. fällt als der erste Faktor, folgt somit 
b)
c)
Graphen zuordnen
Graph I gehört zu  und Graph II zu
und Graph II zu  Koordinatenachsen skalieren
Koordinatenachsen skalieren
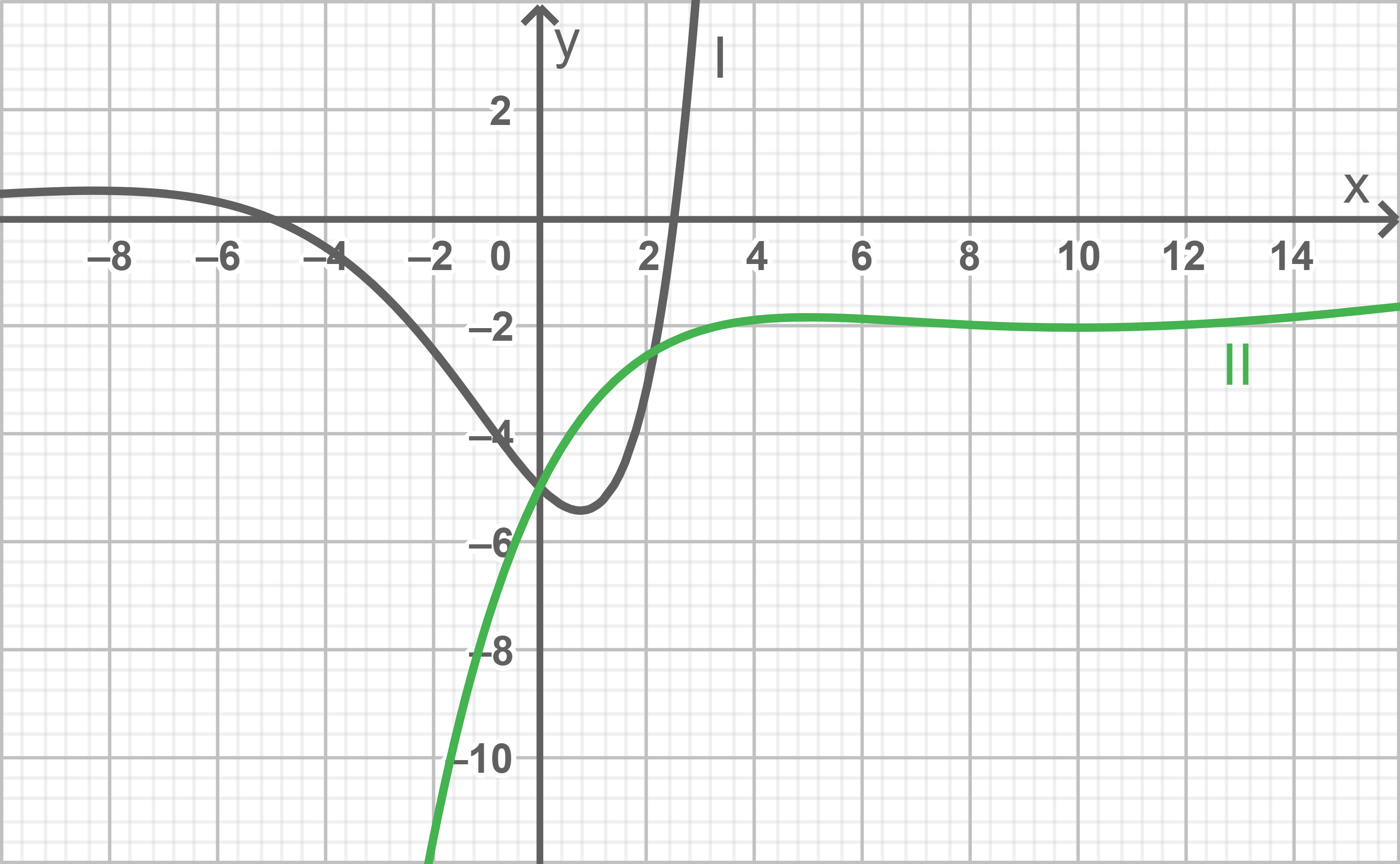 Schnittpunkt angeben
Der gemeinsame Schnittpunkt
Schnittpunkt angeben
Der gemeinsame Schnittpunkt  aller Graphen
aller Graphen  mit der
mit der  -Achse besitzt die Koordinaten
-Achse besitzt die Koordinaten 

d)
Ableiten von 
 im CAS liefert:
im CAS liefert:
 Mit dem solve-Befehl des CAS folgt aus
Mit dem solve-Befehl des CAS folgt aus 
![\(\begin{array}[t]{rll}
x_1&=&5 \\[5pt]
x_2&=&10
\end{array}\)](https://mathjax.schullv.de/d685752dad9448ff4f37eb35620077896b1c1cd465a188b42c4e4173a75b8ba4?color=5a5a5a) Somit sind
Somit sind  und
und  mögliche lokale Extremstellen von
mögliche lokale Extremstellen von 
e)
Aus Aufgabenteil d) folgt, dass  und
und  die einzigen beiden lokalen Extremstellen von
die einzigen beiden lokalen Extremstellen von  sind. Für die
sind. Für die  -Werte der angegebenen Punkte folgt:
-Werte der angegebenen Punkte folgt:
![\(\begin{array}[t]{rll}
f_{-0,2}(5)&=&(-0,2\cdot5^2+5-5) \cdot \mathrm e^{-0,2\cdot5} \\[5pt]
&=&-5\mathrm e^{-1}
\end{array}\)](https://mathjax.schullv.de/63128c610d1b1d6f751fea4a85aaa46a24341955d76abaf8cc76fe79b95946e4?color=5a5a5a)
![\(\begin{array}[t]{rll}
f_{-0,2}(10)&=&(-0,2\cdot10^2+10-5) \cdot \mathrm e^{-0,2\cdot10} \\[5pt]
&=&-15\mathrm e^{-2}
\end{array}\)](https://mathjax.schullv.de/56b8aaf7de3c111eac66a68261c6a0e15be3bbd2f5d33d470364ede9b4e4703f?color=5a5a5a) Für die Steigung
Für die Steigung  der Geraden, die durch diese beiden Punkte verläuft, folgt somit:
der Geraden, die durch diese beiden Punkte verläuft, folgt somit:
 Einsetzen der Koordinaten
Einsetzen der Koordinaten  in die Geradengleichung
in die Geradengleichung  liefert für den
liefert für den  -Achsenabschnitt
-Achsenabschnitt 
![\(\begin{array}[t]{rll}
-5\mathrm e^{-1}&=&-0,038\cdot5+n \\[5pt]
-5\mathrm e^{-1}&=&-0,19+n \quad \scriptsize \mid\;+0,19\\[5pt]
-5\mathrm e^{-1}+0,19&=&n \\[5pt]
-1,65&\approx&n
\end{array}\)](https://mathjax.schullv.de/ca374967d26805b8b0ef693cd18f73cf9ee53e717c05bd534f09d545f860334d?color=5a5a5a) Für die gesuchten Koordinaten des Punkts
Für die gesuchten Koordinaten des Punkts  folgt somit näherungsweise
folgt somit näherungsweise 
f)
Aufgrund der Spiegelung sind die Winkel, die die betrachteten Tangenten an  bzw.
bzw.  mit der
mit der  -Achse und mit der
-Achse und mit der  -Achse einschließen, jeweils gleich groß. Damit das Dreieck gleichseitig ist, müssen alle Innenwinkel
-Achse einschließen, jeweils gleich groß. Damit das Dreieck gleichseitig ist, müssen alle Innenwinkel  betragen, was genau dann der Fall ist wenn sich die Schnittwinkel der Tangenten mit der
betragen, was genau dann der Fall ist wenn sich die Schnittwinkel der Tangenten mit der  -Achse zu
-Achse zu  aufaddieren, das heißt beide
aufaddieren, das heißt beide  betragen. Für die Ableitung von
betragen. Für die Ableitung von  folgt mit dem CAS:
folgt mit dem CAS:
 Für die Steigung
Für die Steigung  der Tangente an
der Tangente an  folgt somit:
folgt somit:
 Gleichsetzen mit
Gleichsetzen mit  liefert nun als einen möglichen Wert für
liefert nun als einen möglichen Wert für 
![\(\begin{array}[t]{rll}
-5a+1&=&\tan(30^\circ) &\quad \scriptsize \mid\;-1\\[5pt]
-5a&=&\tan(30^\circ)-1 &\quad \scriptsize \mid\;:(-5)\\[5pt]
a&=&\dfrac{3-\sqrt{3}}{15}
\end{array}\)](https://mathjax.schullv.de/6b8bd030e5195a5782156d9365e9d328d3f4ab481117fda8b9eb198330ffa230?color=5a5a5a) Gleichsetzen der Steigung
Gleichsetzen der Steigung  mit
mit  liefert für den anderen Wert:
liefert für den anderen Wert:
![\(\begin{array}[t]{rll}
-5a+1&=&\tan(-30^\circ) &\quad \scriptsize \mid\;-1\\[5pt]
-5a&=&\tan(-30^\circ)-1 &\quad \scriptsize \mid\;:(-5)\\[5pt]
a&=&\dfrac{3+\sqrt{3}}{15}
\end{array}\)](https://mathjax.schullv.de/4c6803c3803fb3ca64d88063c8eeb7fc5190348a9f92d1100f11185d763f4ede?color=5a5a5a)
g)
Schritte erläutern
 an den Graphen von
an den Graphen von  die zusätzlich durch den Punkt
die zusätzlich durch den Punkt  verläuft. Bestimme die Koordinaten des Punktes
verläuft. Bestimme die Koordinaten des Punktes  in dem
in dem  an den Graph von
an den Graph von  anliegt.
anliegt.
- Eine Tangentengleichung mit
-Achsenabschnitt
wird aufgestellt, das heißt
schneidet die
-Achse im bekannten Punkt
- Die Steigung
der Tangente ist durch die Steigung der Funktion
an der Stelle
gegeben
- Auflösen der Gleichung
liefert den Wert von
Einsetzen in
ergibt dann
und damit die Koordinaten des Punktes
h)
i)
Da die Seite  vollständig auf der
vollständig auf der  -Achse verläuft, eignet sie sich als Grundseite des Dreiecks. Damit ergibt sich der Flächeninhalt des Dreiecks als
-Achse verläuft, eignet sie sich als Grundseite des Dreiecks. Damit ergibt sich der Flächeninhalt des Dreiecks als  wobei
wobei  die Höhe zur Grundseite
die Höhe zur Grundseite  ist und sich als
ist und sich als  -Koordinate von
-Koordinate von  ergibt. Die Länge von
ergibt. Die Länge von  ergibt sich als Abstand zweier Punkte.
ergibt sich als Abstand zweier Punkte.
j)
Genau dann, wenn  gilt, schneidet der Graph von
gilt, schneidet der Graph von  die
die  -Achse in einem Winkel von
-Achse in einem Winkel von  Da die
Da die  -Funktion nie null wird, kann
-Funktion nie null wird, kann  für kein
für kein  gelten. Auflösen von
gelten. Auflösen von  nach
nach  mit dem solve-Befehl des CAS liefert somit:
mit dem solve-Befehl des CAS liefert somit:

k)
Für die zweite Ableitung von  ergibt sich mit dem CAS:
ergibt sich mit dem CAS:
 1. Schritt: Notwendige Bedingung für Extremstellen anwenden
1. Schritt: Notwendige Bedingung für Extremstellen anwenden
 Mit dem solve-Befehl das CAS ergibt sich:
Mit dem solve-Befehl das CAS ergibt sich:
 2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
2. Schritt: Hinreichende Bedingung für Extremstellen überprüfen
![\(\begin{array}[t]{rll}
h_a](https://mathjax.schullv.de/003fae687d968facc0ccb8d40e0f113e79f1f5a250c3140c0105a8eb83f4b37d?color=5a5a5a) Somit besitzt der Graph von
Somit besitzt der Graph von  an der Stelle
an der Stelle  einen Tiefpunkt.
3. Schritt: Koordinaten bestimmen
einen Tiefpunkt.
3. Schritt: Koordinaten bestimmen
![\(\begin{array}[t]{rll}
h_a(a)&=&\mathrm e^{a-a}+a-a \\[5pt]
&=&1
\end{array}\)](https://mathjax.schullv.de/3bd96066a8f2ffaf19f3fc2fd020bb3a58304d9423a6c194b473c0b9adcc785d?color=5a5a5a) Der einzige Extrempunkt jedes Graphen der Funktionenschar ist somit ein Tiefpunkt, der oberhalb der
Der einzige Extrempunkt jedes Graphen der Funktionenschar ist somit ein Tiefpunkt, der oberhalb der  -Achse liegt. Daher kann keiner der Graphen der Funktionenschar eine Nullstelle besitzen.
-Achse liegt. Daher kann keiner der Graphen der Funktionenschar eine Nullstelle besitzen.
l)
m)
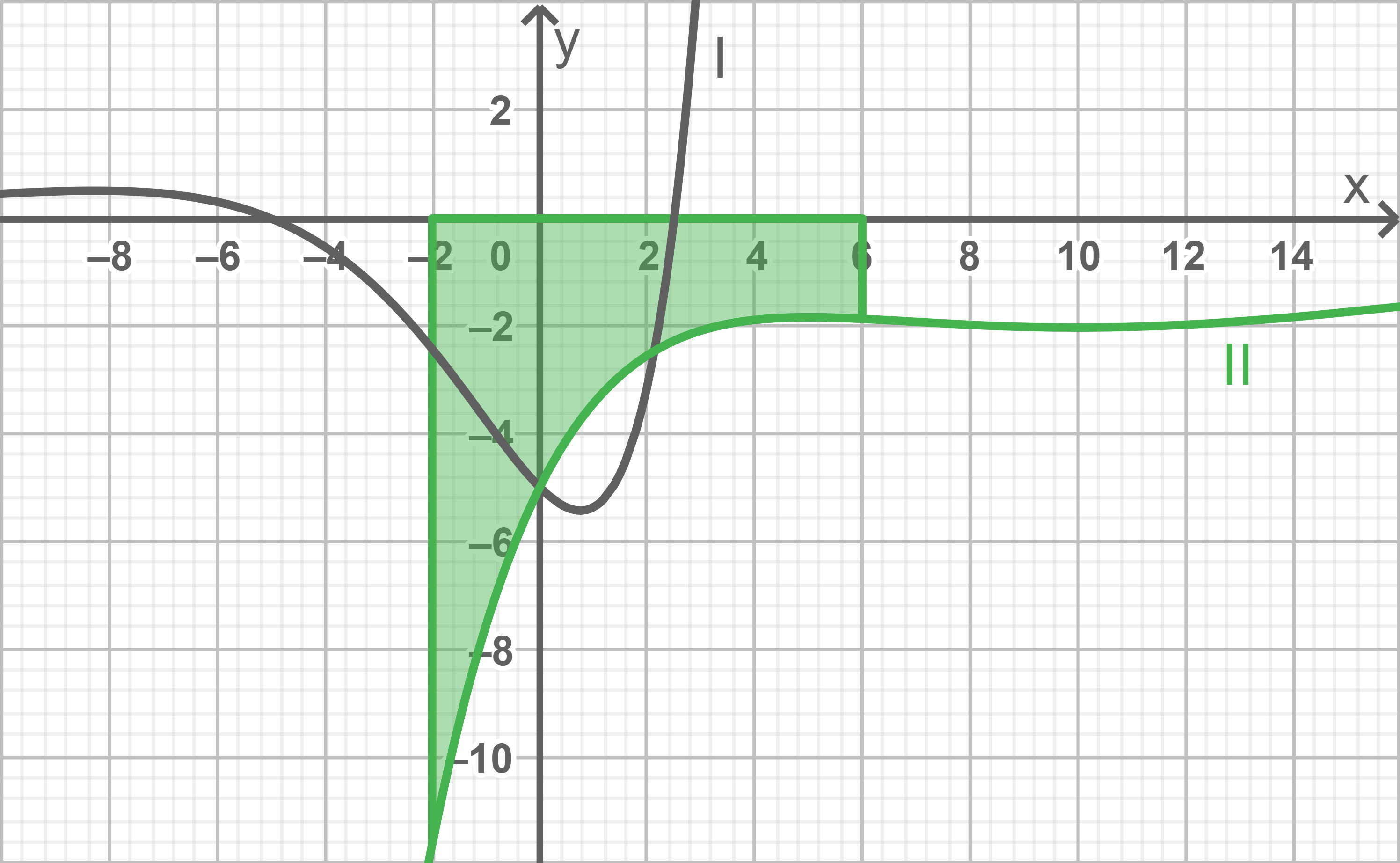
Da aufgrund der Achsenbeschriftung jedes Kästchen