Analytische Geometrie 3.1 - Pyramiden
Betrachtet werden die Pyramiden  mit
mit 
 ,
,  und
und  , wobei
, wobei  gilt.
gilt.
Die Abbildung 1 zeigt eine dieser Pyramiden.
Die Abbildung 1 zeigt eine dieser Pyramiden.
a)
Begründe, dass das Dreieck  gleichschenklig ist.
gleichschenklig ist.
(2 BE)
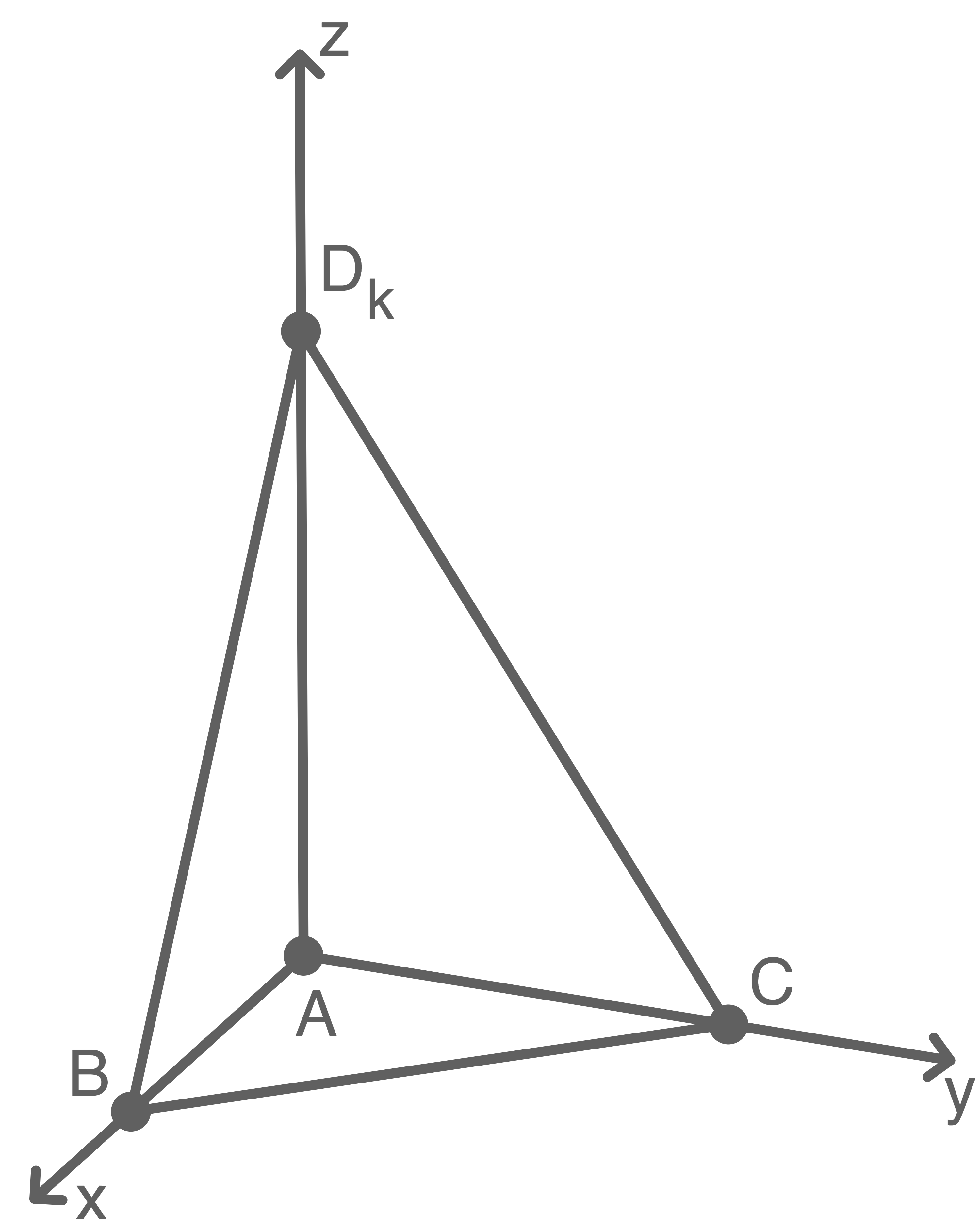
Abb. 1
b)
Der Mittelpunkt der Strecke  ist
ist  . Begründe, dass
. Begründe, dass  die Länge einer Höhe des Dreiecks
die Länge einer Höhe des Dreiecks  ist.
ist.
Bestimme den Flächeninhalt des Dreiecks .
.
Für jeden Wert von Bestimme den Flächeninhalt des Dreiecks
(3 BE)
c)
Bestimme eine Gleichung von  in Koordinatenform.
in Koordinatenform.
 Zur Kontrolle:
Zur Kontrolle: 

(4 BE)
d)
Ermittle denjenigen Wert von  , für den die Größe des Winkels, unter dem die
, für den die Größe des Winkels, unter dem die  -Achse die Ebene
-Achse die Ebene  schneidet,
schneidet,  beträgt.
beträgt.
(4 BE)
e)
Die Punkte  ,
,  ,
,  und
und  sind ebenfalls Eckpunkte einer Pyramide.
sind ebenfalls Eckpunkte einer Pyramide.
Ermittle, um wie viel Prozent das Volumen dieser Pyramide größer ist als das Volumen der Pyramide .
.
Ermittle, um wie viel Prozent das Volumen dieser Pyramide größer ist als das Volumen der Pyramide
(3 BE)
f)
Bestimme den Abstand des Punktes  von der Ebene
von der Ebene  .
.
(2 BE)
g)
Der Punkt  wird an der Ebene
wird an der Ebene  gespiegelt. Ermittle die Koordinaten des Spiegelpunktes
gespiegelt. Ermittle die Koordinaten des Spiegelpunktes  .
.
(4 BE)
Zusätzlich zu den Pyramiden wird der in der Abbildung 2 gezeigte Quader betrachtet. Die Punkte  und
und  sind Eckpunkte des Quaders, die Seitenflächen des Quaders sind parallel zu den Koordinatenebenen.
sind Eckpunkte des Quaders, die Seitenflächen des Quaders sind parallel zu den Koordinatenebenen.
Für enthält die Seitenfläche
enthält die Seitenfläche  der Pyramide den Eckpunkt
der Pyramide den Eckpunkt  des Quaders.
des Quaders.
Für kleinere Werte von schneidet die Seitenfläche
schneidet die Seitenfläche  den Quader in einem Vieleck.
den Quader in einem Vieleck.
Für
Für kleinere Werte von
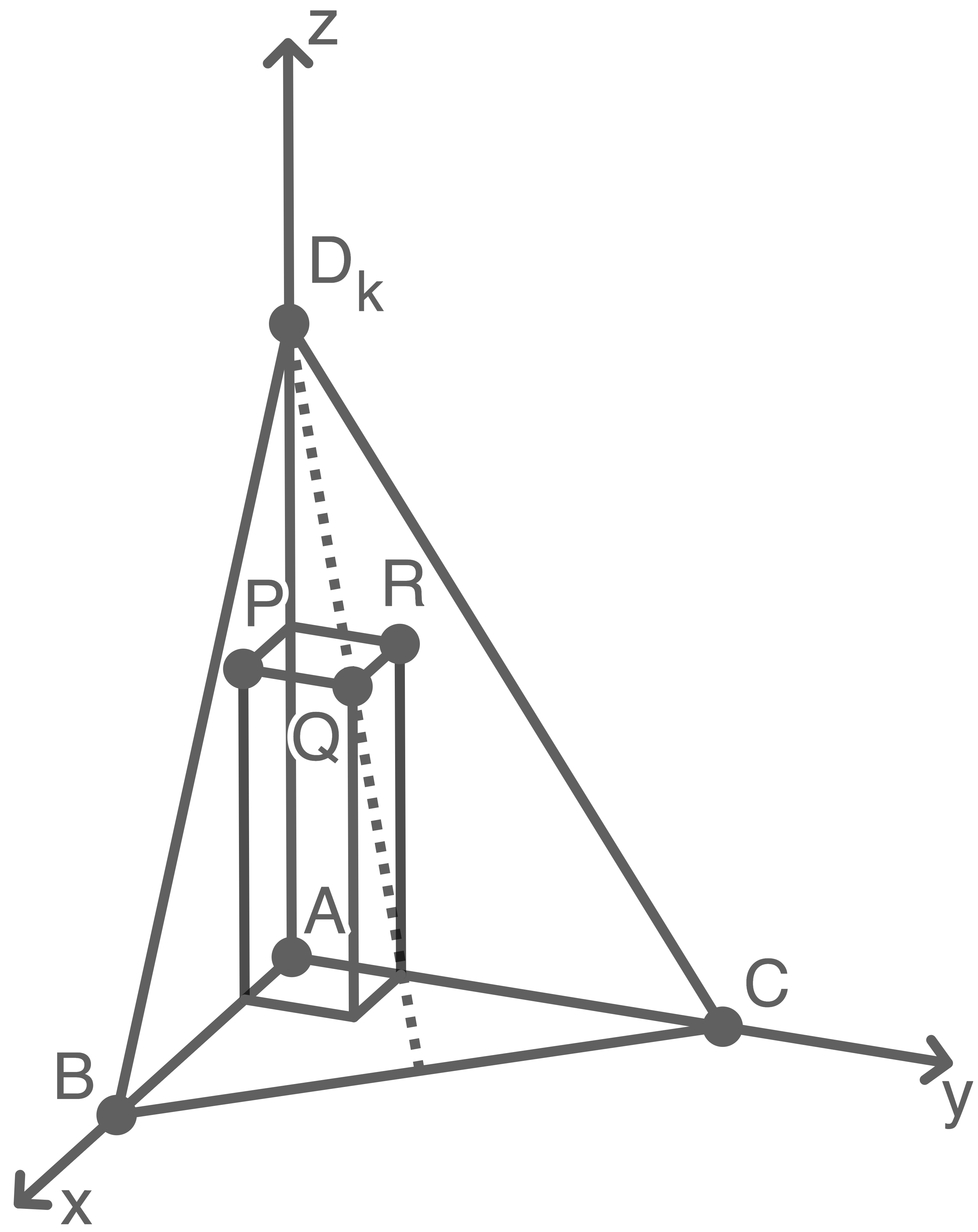
Abb. 2
h)
Für einen Wert von  verläuft die Seitenfläche
verläuft die Seitenfläche  durch die Eckpunkte
durch die Eckpunkte  und
und  des Quaders. Bestimme diesen Wert von
des Quaders. Bestimme diesen Wert von  .
.
 Zur Kontrolle:
Zur Kontrolle: 

(3 BE)
i)
Bestimme für  das Teilverhältnis, in dem der Punkt
das Teilverhältnis, in dem der Punkt  die Strecke
die Strecke  teilt.
teilt.
(2 BE)
j)
Gib in Abhängigkeit von  die Anzahl der Eckpunkte des Vielecks an, in dem die Seitenfläche
die Anzahl der Eckpunkte des Vielecks an, in dem die Seitenfläche  den Quader schneidet.
den Quader schneidet.
(4 BE)
k)
Nun wird die Pyramide  , d.h. diejenige für
, d.h. diejenige für  , betrachtet. Dieser Pyramide werden Quader mit quadratischer Grundfläche einbeschrieben; der Punkt
, betrachtet. Dieser Pyramide werden Quader mit quadratischer Grundfläche einbeschrieben; der Punkt  ist gemeinsamer Eckpunkt der Quader. Die Seitenflächen der Quader sind parallel zu den Koordinatenebenen. Die Höhe
ist gemeinsamer Eckpunkt der Quader. Die Seitenflächen der Quader sind parallel zu den Koordinatenebenen. Die Höhe  der Quader durchläuft alle Werte mit
der Quader durchläuft alle Werte mit  . Für jeden Wert von
. Für jeden Wert von  liegt der Eckpunkt
liegt der Eckpunkt  in der Seitenfläche
in der Seitenfläche  der Pyramide. Die Abbildung 3 zeigt einen dieser Quader.
der Pyramide. Die Abbildung 3 zeigt einen dieser Quader.
Ermittle die Koordinaten des Punktes in Abhängigkeit von
in Abhängigkeit von  .
.
Ermittle die Koordinaten des Punktes
(4 BE)
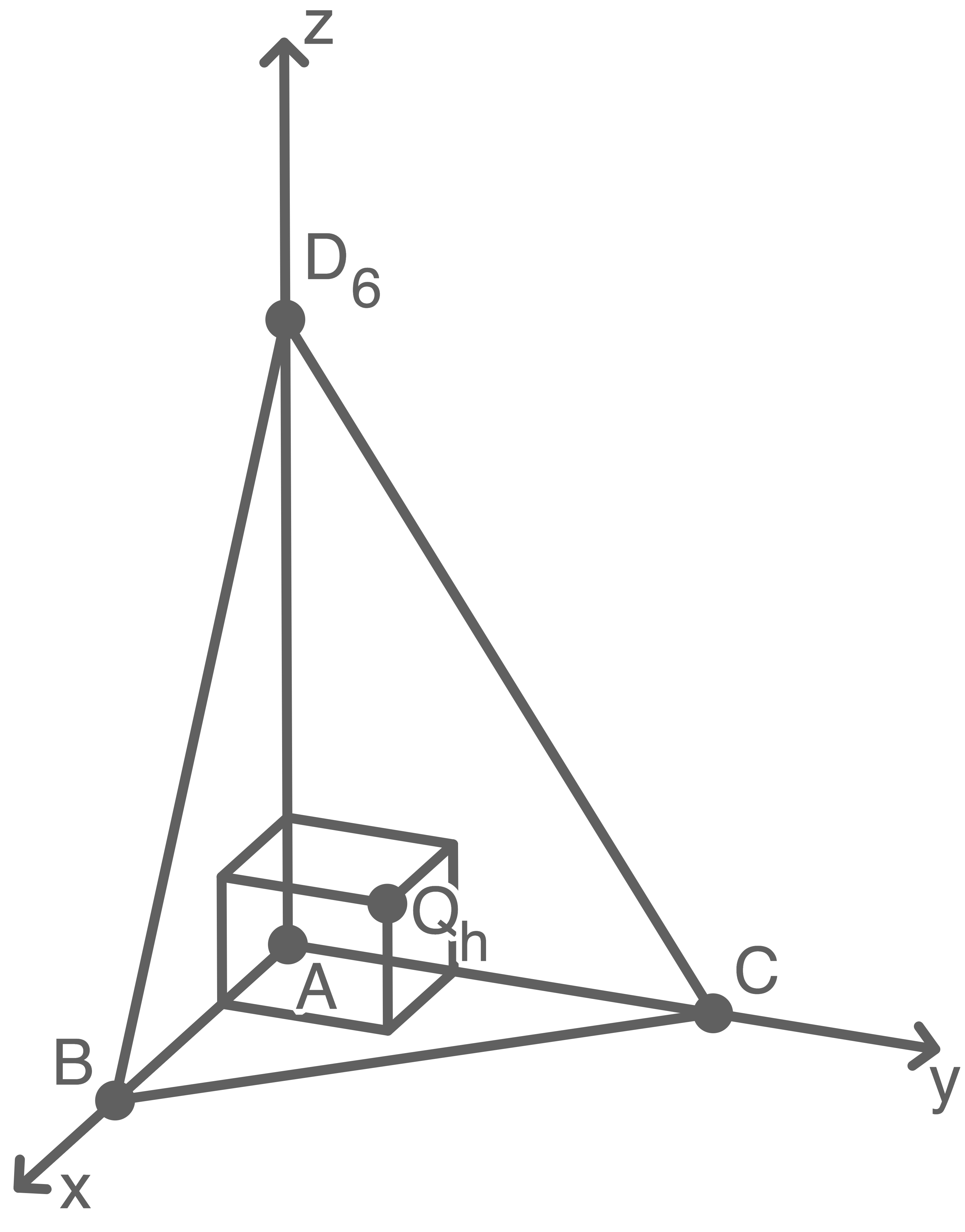
Abb. 3
l
Eine Ebene  , die parallel zur
, die parallel zur  -Ebene liegt, schneidet die Pyramide
-Ebene liegt, schneidet die Pyramide  so, dass die beiden entstehenden Teilkörper das gleiche Volumen haben.
so, dass die beiden entstehenden Teilkörper das gleiche Volumen haben.
Ermittle die Stelle, an der die Ebene die
die  -Achse schneidet.
-Achse schneidet.
Ermittle die Stelle, an der die Ebene
(5 BE)
(40 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
Die Dreicke  und
und  sind beide rechtwinklig und haben gleich lange Katheten. Folglich müssen auch ihre Hypothenusen gleich lang sein, die gerade den beiden Schenkel des Dreiecks
sind beide rechtwinklig und haben gleich lange Katheten. Folglich müssen auch ihre Hypothenusen gleich lang sein, die gerade den beiden Schenkel des Dreiecks  entsprechen.
entsprechen.
b)
Höhe des Dreiecks begründen
Da das Dreieck  mit der Grundseite
mit der Grundseite  gleichschenklig ist, ist die Höhe durch die Länge der Strecke zwischen dem Mittelpunkt von
gleichschenklig ist, ist die Höhe durch die Länge der Strecke zwischen dem Mittelpunkt von  mit dem Punkt
mit dem Punkt  gegeben. Diese entspricht gerade
gegeben. Diese entspricht gerade  Flächeninhalt bestimmen
Flächeninhalt bestimmen

c)
Da die Ebene nicht durch den Ursprung verläuft, eignet sich die Darstellung  für die Ebene
für die Ebene  Einsetzen der Koordinaten des Punktes
Einsetzen der Koordinaten des Punktes  liefert
liefert  Einsetzten der Koordinaten des Punktes
Einsetzten der Koordinaten des Punktes  liefert
liefert  Einsetzten der Koordinaten des Punktes
Einsetzten der Koordinaten des Punktes  liefert die Gleichung
liefert die Gleichung  also
also  Die Ebenengleichung ist also gegeben durch
Die Ebenengleichung ist also gegeben durch 
d)
e)
Die Pyramide  kann in die Pyramiden
kann in die Pyramiden  und
und  aufgeteilt werden. Beide Pyramiden haben dann das Dreieck
aufgeteilt werden. Beide Pyramiden haben dann das Dreieck  als Grundfläche.
Es gilt
als Grundfläche.
Es gilt  und
und  Die Pyramide
Die Pyramide  hat also ein um
hat also ein um  größeres Volumen als die Pyramide
größeres Volumen als die Pyramide 
f)
Der Abstand kann mithilfe der hesseschen Normalform berechnet werden.





 Der Abstand von der Ebene
Der Abstand von der Ebene  zum Punkt
zum Punkt  beträgt
beträgt 
g)
Die Lotgerade durch den Punkt  und die Ebene
und die Ebene  ist gegeben durch
ist gegeben durch  Der Schnittpunkt von
Der Schnittpunkt von  mit
mit  lässt durch Einsetzen der Koordinaten in die Ebenengleichung bestimmen:
lässt durch Einsetzen der Koordinaten in die Ebenengleichung bestimmen:
![\(\begin{array}[t]{rll}
t+t+\dfrac{1}{2}\left(-1+\dfrac{t}{2}\right)&=& 4 \\[5pt]
-\dfrac{1}{2}+\dfrac{9t}{4}&=& 4 \quad \scriptsize \mid\; +\dfrac{1}{2} \\[5pt]
\dfrac{9t}{4}&=& \dfrac{9}{2} \quad \scriptsize \mid\; \cdot \dfrac{4}{9} \\[5pt]
t&=& 2
\end{array}\)](https://mathjax.schullv.de/fa791b2505d3afc1b4599d5594bd16b5b7e331a781d5af7ed53f79c72418a690?color=5a5a5a)
 Der Punkt
Der Punkt  hat die Koordianten
hat die Koordianten 
h)
Einsetzen der Koordinaten des Punktes  in
in  liefert:
liefert:
![\(\begin{array}[t]{rll}
1\cdot1+1\cdot 0 +\dfrac{4}{k}\cdot 3&=& 4 \\[5pt]
1 +\dfrac{12}{k}&=& 4 \quad \scriptsize \mid\;-1 \\[5pt]
\dfrac{12}{k}&=& 3 \quad \scriptsize \mid\;\cdot k \\[5pt]
12&=& 3k \quad \scriptsize \mid\; :3 \\[5pt]
4&=& k \\
k&=& 4
\end{array}\)](https://mathjax.schullv.de/547eb358f85ad5788e17f506bf925070eb47b315d365938b102dad3f1792213b?color=5a5a5a)
i)
Der Punkt  hat die
hat die  -Koordinate
-Koordinate  der Punkt
der Punkt  hat die
hat die  -Koordinate
-Koordinate  Damit teilt der Punkt
Damit teilt der Punkt  die Strecke
die Strecke  im Verhältnis
im Verhältnis 
j)
Aus den vorherigen Teilaufgaben ist bekannt:
 den Punkt mit den Koordinaten
den Punkt mit den Koordinaten  für
für 
![\(\begin{array}[t]{rll}
1\cdot 0+1\cdot 0+\dfrac{4}{k}\cdot 3&=& 4 \\[5pt]
\dfrac{12}{k}&=& 4 \quad \scriptsize \mid\; \cdot \dfrac{k}{4} \\[5pt]
3&=& k \\[5pt]
k&=& 3
\end{array}\)](https://mathjax.schullv.de/96b8e65aad0f9a8a0a5ff6570c6278e1315f34fcd770b85ce417265ae2c692cd?color=5a5a5a) Damit lässt sich für die Anzahl an Eckpunkten in Abhängigkeit von
Damit lässt sich für die Anzahl an Eckpunkten in Abhängigkeit von  folgern:
folgern:
 drei Eckpunkte
drei Eckpunkte
 fünf Eckpunkte
fünf Eckpunkte
 vier Eckpunkte
vier Eckpunkte
- Für
schneidet die Ebene den Quader in genau einem Punkt, für
also in keinem Punkt
- Für
schneidet
den Quader in den Punkten
und
k)
Der Punkt  liegt auf der Strecke
liegt auf der Strecke  und hat die
und hat die  -Koordiante
-Koordiante  Die Strecke
Die Strecke  liegt auf der Geraden mit folgender Gleichung:
Damit ein Punkt auf dieser Geraden die
liegt auf der Geraden mit folgender Gleichung:
Damit ein Punkt auf dieser Geraden die  -Koordinate
-Koordinate  hat, muss
hat, muss  gelten. Damit gilt für die restlichen Koordinaten
gelten. Damit gilt für die restlichen Koordinaten  Die Koordinaten des Punktes
Die Koordinaten des Punktes  lauten
lauten 
l)
Es bezeichnet  den Abstand des Schnittpunkts von
den Abstand des Schnittpunkts von  mit der
mit der  -Achse und dem Punkt
-Achse und dem Punkt  Die Ebene
Die Ebene  schneidet die Strecke
schneidet die Strecke  dann bei
dann bei  und die Strecke
und die Strecke  bei
bei  Das Volumen der abgetrennten Pyramide lässt sich damit wie folgt berechnen:
Grundseite:
Das Volumen der abgetrennten Pyramide lässt sich damit wie folgt berechnen:
Grundseite: 
Höhe:
 Das Volumen der gesamten Pyramide ist gegeben durch
Das Volumen der gesamten Pyramide ist gegeben durch  Es muss also gelten:
Es muss also gelten:
![\(\begin{array}[t]{rll}
\dfrac{1}{4}f^3 &=& \dfrac{1}{2}\cdot 16 \quad \scriptsize \mid\; \cdot 4 \\[5pt]
f^3 &=& 32 \quad \scriptsize \mid\; \sqrt[3]{} \\[5pt]
f &\approx& 3,2
\end{array}\)](https://mathjax.schullv.de/7183a38ed23086207ba1e52c790e753861998d7b60c0e553d05de20f7ba444c8?color=5a5a5a) Damit lässt sich der gesuchte Wert von
Damit lässt sich der gesuchte Wert von  berechnen:
berechnen:

Höhe: