Analysis 1
a)
Die folgende Abbildung stellt einen achsensymmetrischen Querschnitt des Rumpfes einer Segelyacht vereinfacht in einem Koordinatensystem dar. Die  -Achse beschreibt die Lage der Wasseroberfläche und die
-Achse beschreibt die Lage der Wasseroberfläche und die  -Achse verläuft entlang der Symmetrieachse. Dabei entspricht eine Längeneinheit einem Meter in der Wirklichkeit.
-Achse verläuft entlang der Symmetrieachse. Dabei entspricht eine Längeneinheit einem Meter in der Wirklichkeit.
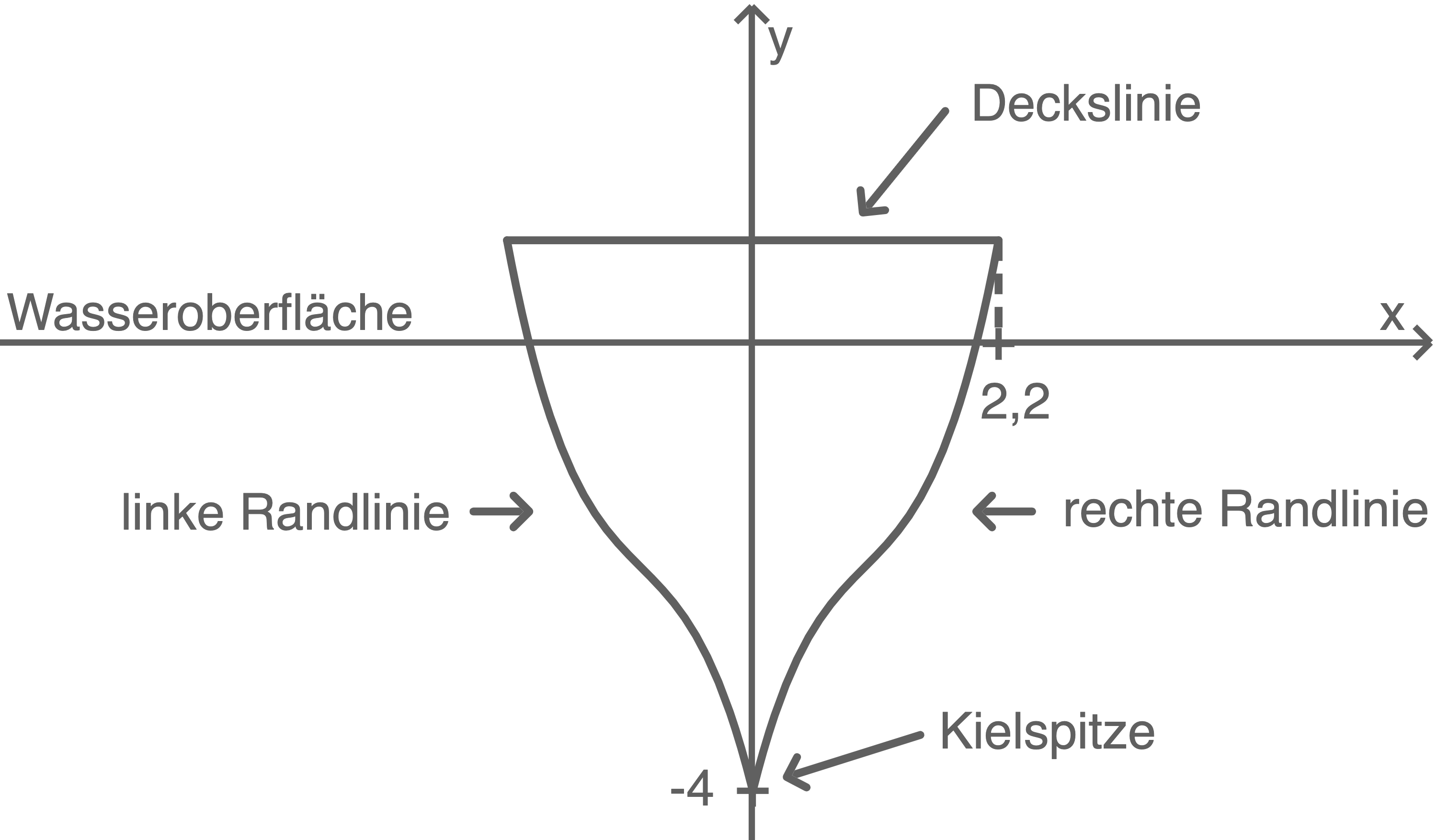 Die rechte Randlinie wird mithilfe der Funktion
Die rechte Randlinie wird mithilfe der Funktion  mit
mit  für
für  modelliert.
modelliert.

a1)
Berechne die Breite des Querschnitts auf Höhe der Wasseroberfläche und zeige, dass die Deckslinie ca.  über der Wasseroberfläche liegt.
über der Wasseroberfläche liegt.
(3 BE)
a2)
Weise nach, dass der Graph von  im Intervall
im Intervall ![\([0 ; 2,2]\)](https://mathjax.schullv.de/eacc030304b140cf23bf537f1011c790cc73f4ae4ac33e23c1099ef14b0b5b20?color=5a5a5a) eine Wendestelle besitzt, und gib die Koordinaten des Wendepunktes an.
eine Wendestelle besitzt, und gib die Koordinaten des Wendepunktes an.
(4 BE)
a3)
Berechne die Größe des Winkels, der sich aus der rechten und der linken Randlinie an der Kielspitze im Inneren des Querschnitts ergibt.
(4 BE)
a4)
Bestimme den Flächeninhalt des Querschnitts.
(4 BE)
b)
Bei der Trainingsfahrt einer Rennyacht wird ihre Geschwindigkeit durch die Funktion  mit
mit  mit
mit  beschrieben. Dabei gibt
beschrieben. Dabei gibt  die Zeit in Sekunden
die Zeit in Sekunden  nach Beginn der Zeitmessung an und
nach Beginn der Zeitmessung an und  die Geschwindigkeit in Meter pro Sekunde
die Geschwindigkeit in Meter pro Sekunde 
b1)
Zeige, dass die mittlere Änderungsrate der Geschwindigkeit im Zeitraum von  bis
bis  nach Beginn der Zeitmessung ungefähr gleich der momentanen Änderungsrate der Geschwindigkeit
nach Beginn der Zeitmessung ungefähr gleich der momentanen Änderungsrate der Geschwindigkeit  nach Beginn der Zeitmessung ist.
nach Beginn der Zeitmessung ist.
(4 BE)
b2)
Begründe anhand des Funktionsterms von  dass die Geschwindigkeit der Yacht stets kleiner als
dass die Geschwindigkeit der Yacht stets kleiner als  ist.
ist.
(2 BE)
b3)
Der Wert des Terms  gibt die Länge des zurückgelegten Weges in Metern innerhalb des Zeitraums von
gibt die Länge des zurückgelegten Weges in Metern innerhalb des Zeitraums von  bis
bis  Sekunden an.
Bestimme den Wert für
Sekunden an.
Bestimme den Wert für  so dass diese Länge
so dass diese Länge  beträgt.
beträgt.
(2 BE)
c)
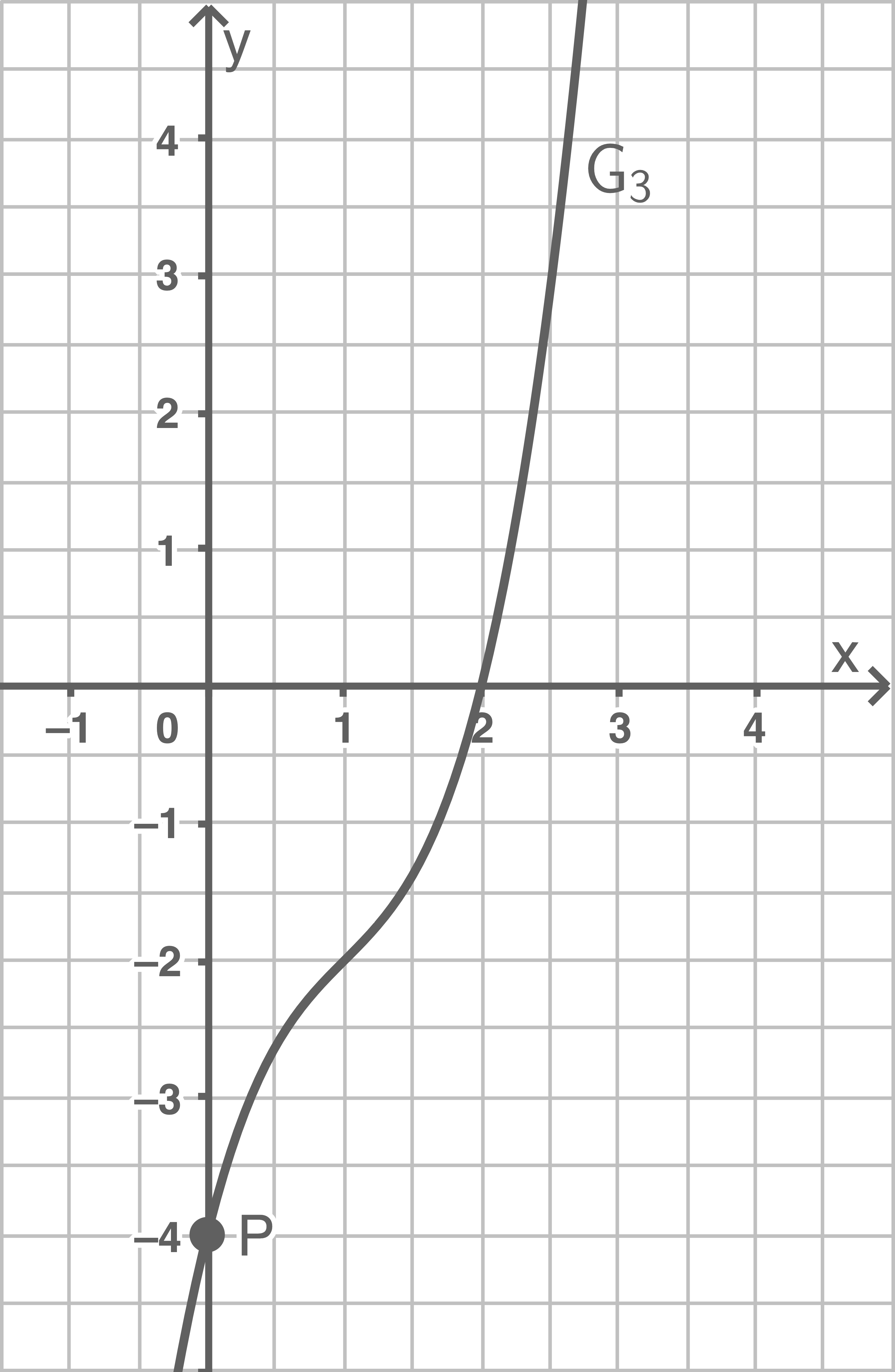
Gegeben ist die Schar der auf  definierten Funktionen
definierten Funktionen  mit
mit  und
und  Der Graph jeder Funktion
Der Graph jeder Funktion  wird mit
wird mit  bezeichnet. Jeder Graph
bezeichnet. Jeder Graph  verläuft durch den Punkt
verläuft durch den Punkt  Die folgende Abbildung zeigt
Die folgende Abbildung zeigt 

c1)
Zeige, dass jeweils zwei verschiedene Graphen  und
und  nur den Punkt
nur den Punkt  gemeinsam haben.
gemeinsam haben.
(3 BE)
c2)
Bestimme alle Werte von  so dass
so dass  keine waagerechte Tangente besitzt.
keine waagerechte Tangente besitzt.
(4 BE)
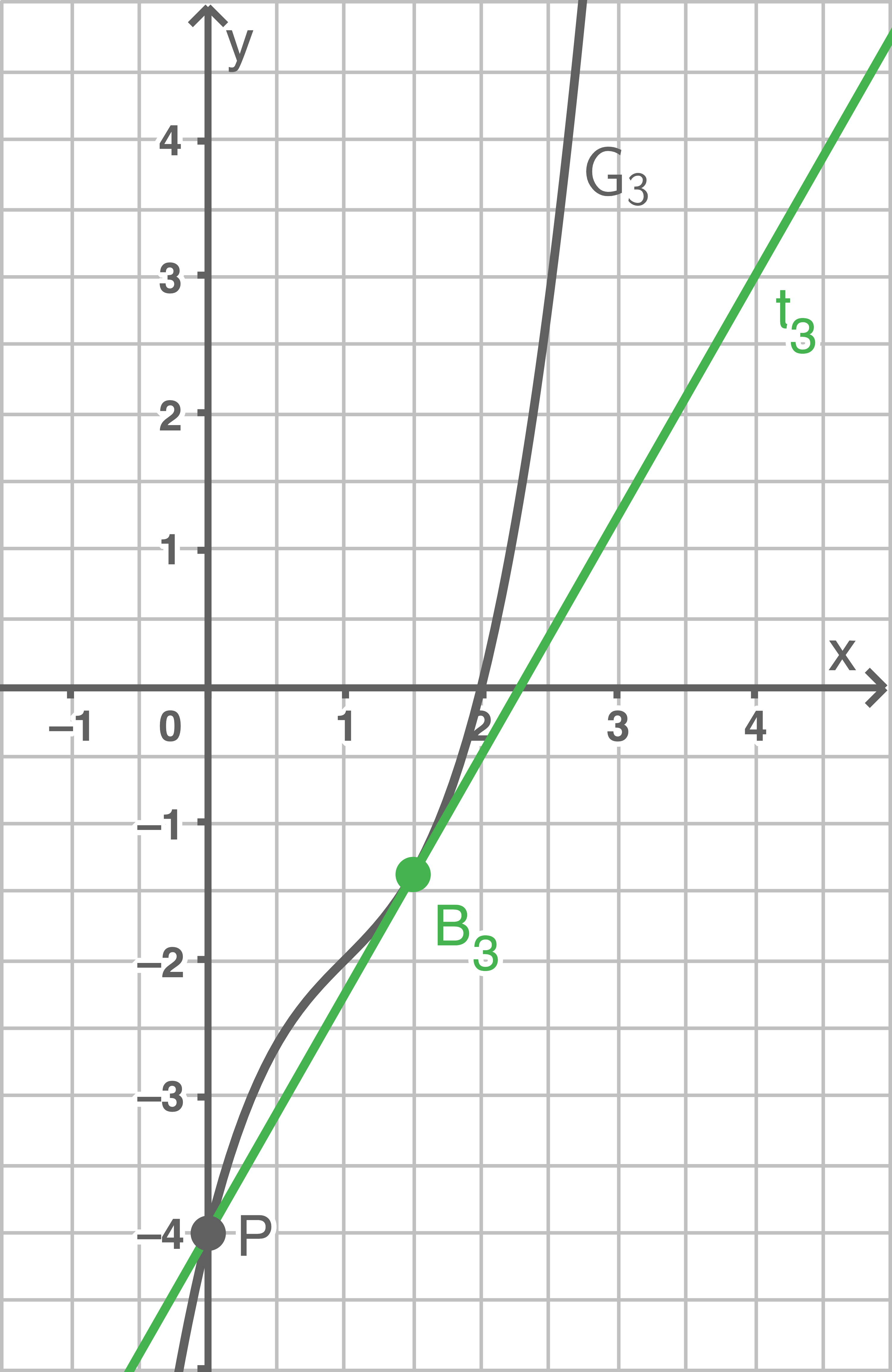
c3)
Auf jedem Graphen  liegt genau ein von
liegt genau ein von  verschiedener Punkt
verschiedener Punkt  so dass die dort angelegte Tangente
so dass die dort angelegte Tangente  durch
durch  verläuft.
verläuft.
- Zeichne
und
in die Abbildung ein.
- Berechne die
-Koordinate des Berührpunktes
in Abhängigkeit von
(6 BE)
c4)
Zeige für jeden Punkt  auf dem Graphen
auf dem Graphen  Die im Punkt
Die im Punkt  angelegte Tangente
angelegte Tangente  hat höchstens einen weiteren gemeinsamen Punkt mit
hat höchstens einen weiteren gemeinsamen Punkt mit 
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a1)
Breite berechnen
Der CAS liefert aus  für die Nullstelle von
für die Nullstelle von  im Bereich
im Bereich  den Wert
den Wert  Aufgrund der Symmetrie und wegen
Aufgrund der Symmetrie und wegen  beträgt die Breite des Querschnitts auf Höhe der Wasseroberfläche
beträgt die Breite des Querschnitts auf Höhe der Wasseroberfläche  Höhe der Deckslinie über der Wasseroberfläche zeigen
Die Deckslinie liegt somit ca.
Höhe der Deckslinie über der Wasseroberfläche zeigen
Die Deckslinie liegt somit ca.  über der Wasseroberfläche.
über der Wasseroberfläche.
a2)
Wendestelle nachweisen


 Notwendige Bedingung für eine Wendestelle überprüfen:
Notwendige Bedingung für eine Wendestelle überprüfen:
 Mit Hilfe des CAS folgt
Mit Hilfe des CAS folgt  Hinreichende Bedingung für eine Wendestelle überprüfen:
Hinreichende Bedingung für eine Wendestelle überprüfen:
 Bei
Bei  liegt also eine Wendestelle im Intervall
liegt also eine Wendestelle im Intervall ![\([0;2,2]\)](https://mathjax.schullv.de/2202acb3515c43403a3894e266e51a5f3891a6c46f15b4019f15bce848c356a3?color=5a5a5a) vor.
Koordinaten angeben
vor.
Koordinaten angeben

 Der Wendepunkt hat somit die Koordinaten
Der Wendepunkt hat somit die Koordinaten 
a3)
a4)
Der Flächeninhalt des Querschnitts im Bereich der positiven  -Achse ist gegeben durch die Fläche zwischen der Deckslinie und dem Graphen der Funktion
-Achse ist gegeben durch die Fläche zwischen der Deckslinie und dem Graphen der Funktion  Aufgrund der Symmetrie folgt für den gesamten Flächeninhalt:
Der Flächeninhalt des Querschnitts beträgt also etwa
Aufgrund der Symmetrie folgt für den gesamten Flächeninhalt:
Der Flächeninhalt des Querschnitts beträgt also etwa 
b1)
Die mittlere Änderungsrate der Geschwindigkeit im Zeitraum von  bis
bis  wird wie folgt berechnet:
Die momentane Änderungsrate der Geschwindigkeit bei
wird wie folgt berechnet:
Die momentane Änderungsrate der Geschwindigkeit bei  wird durch die Ableitung der Funktion
wird durch die Ableitung der Funktion  bestimmt:
bestimmt:
 Einsetzen von
Einsetzen von  ergibt:
ergibt:

 Da die mittlere Änderungsrate und die momentane Änderungsrate übereinstimmen, ist die Aussage gezeigt.
Da die mittlere Änderungsrate und die momentane Änderungsrate übereinstimmen, ist die Aussage gezeigt.
b2)
Die Funktion  beschreibt die Geschwindigkeit der Yacht. Da für alle Werte von
beschreibt die Geschwindigkeit der Yacht. Da für alle Werte von  stets
stets  gilt, folgt:
gilt, folgt:
 Somit ist die Geschwindigkeit der Yacht stets kleiner als
Somit ist die Geschwindigkeit der Yacht stets kleiner als 
b3)
Gesucht ist die Lösung der Gleichung  Mit dem CAS folgt
Mit dem CAS folgt 
c1)
Da  vorausgesetzt ist, ergibt sich keine weitere Lösung für
vorausgesetzt ist, ergibt sich keine weitere Lösung für  außer
außer  . Die beiden Funktionen haben also nur den Punkt
. Die beiden Funktionen haben also nur den Punkt  gemeinsam.
gemeinsam.
c2)
Eine waagerechte Tangente liegt vor, wenn die Steigung  ist. Gesucht ist also die Lösung der folgenden Gleichung:
ist. Gesucht ist also die Lösung der folgenden Gleichung:
![\(\begin{array}[t]{rll}
f_k](https://mathjax.schullv.de/99c23e113df67631afac1d1eb57673f0d2325cac08faa0d5d0e9346bdbab1b04?color=5a5a5a) Mit der pq-Formel ergibt sich:
Mit der pq-Formel ergibt sich:
 Damit
Damit  keine Lösung hat, muss der Ausdruck unter der Wurzel negativ sein:
keine Lösung hat, muss der Ausdruck unter der Wurzel negativ sein:
![\(\begin{array}[t]{rll}
\left(-\dfrac{k}{3}\right)^2 - \dfrac{4}{3} &\lt& 0 \\[5pt]
\dfrac{k^2}{9} - \dfrac{4}{3} &\lt& 0 &\quad \scriptsize \mid\; +\dfrac{4}{3} \\[5pt]
\dfrac{k^2}{9} &\lt& \dfrac{4}{3} &\quad \scriptsize \mid\; \cdot 9 \\[5pt]
k^2 &\lt& 12 &\quad \scriptsize \mid\; \sqrt{\ } \\[5pt]
k &\lt& \sqrt{12}
\end{array}\)](https://mathjax.schullv.de/99d5ef64b26f43dbb9e7d35db144170be79a330446fc845408a864be565c9dbf?color=5a5a5a) Somit besitzt
Somit besitzt  für
für  keine waagerechte Tangente.
keine waagerechte Tangente.
c3)
c4)
Die Tangente  an den Graphen
an den Graphen  im Punkt
im Punkt  ist wie folgt gegeben:
ist wie folgt gegeben:
 Mit Hilfe des CAS liefert die Gleichung
Mit Hilfe des CAS liefert die Gleichung  die folgenden beiden Lösungen:
die folgenden beiden Lösungen:
![\(\begin{array}[t]{rll}
x_1&=&k-2q \\[5pt]
x_2&=&q
\end{array}\)](https://mathjax.schullv.de/876d4f08f123714bd731f2da62da781c6fbce4091831848c056f5e343edff254?color=5a5a5a) Da
Da  die
die  -Koordinate von
-Koordinate von  ist und es nur eine weitere Lösung gibt, ist die Aussage somit wahr.
ist und es nur eine weitere Lösung gibt, ist die Aussage somit wahr.