Analysis 2

Auf einer Autobahn entsteht morgens an einer Baustelle häufig ein Stau, der sich dann wieder vollständig auflöst.

An einem bestimmten Tag entsteht der Stau um 6:00 Uhr und löst sich bis 10:00 Uhr vollständig auf. Für diesen Stau kann mithilfe der in $\mathbb{R}$ definierten Funktion $f$ mit

$f(x)=x \cdot(8-5 x) \cdot\left(1-\frac{x}{4}\right)^2$

für $0 \leq x \leq 4$ beschrieben werden, wie stark die Staulänge zunimmt bzw. abnimmt. Dabei gibt $x$ die nach 6:00 Uhr vergangene Zeit in Stunden und $f(x)$ die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.

a1)

Nenne die Uhrzeiten, zu denen die momentane Änderungsrate der Staulänge den Wert null hat.

(3 P)

a2)

Es gilt $f(2)\lt 0.$
Gib die Bedeutung dieser Tatsache im Sachzusammenhang an.

(1 P)

a3)

Berechne den Zeitpunkt, zu dem die Staulänge am stärksten zunimmt.

(5 P)

a4)

Gib den Zeitpunkt an, zu dem der Stau am längsten ist.
Begründe deine Angabe.

(2 P)

Im Sachzusammenhang ist neben der Funktion $f$ die in $\mathbb{R}$ definierte Funktion $s$ mit $s(x)=-\frac{1}{16} x^5+\frac{3}{4} x^4-3 x^3+4 x^2$ von Bedeutung.

b1)

Begründe, dass die folgende Aussage richtig ist:

Die Staulänge kann für jeden Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion $s$ angegeben werden.

(2 P)

b2)

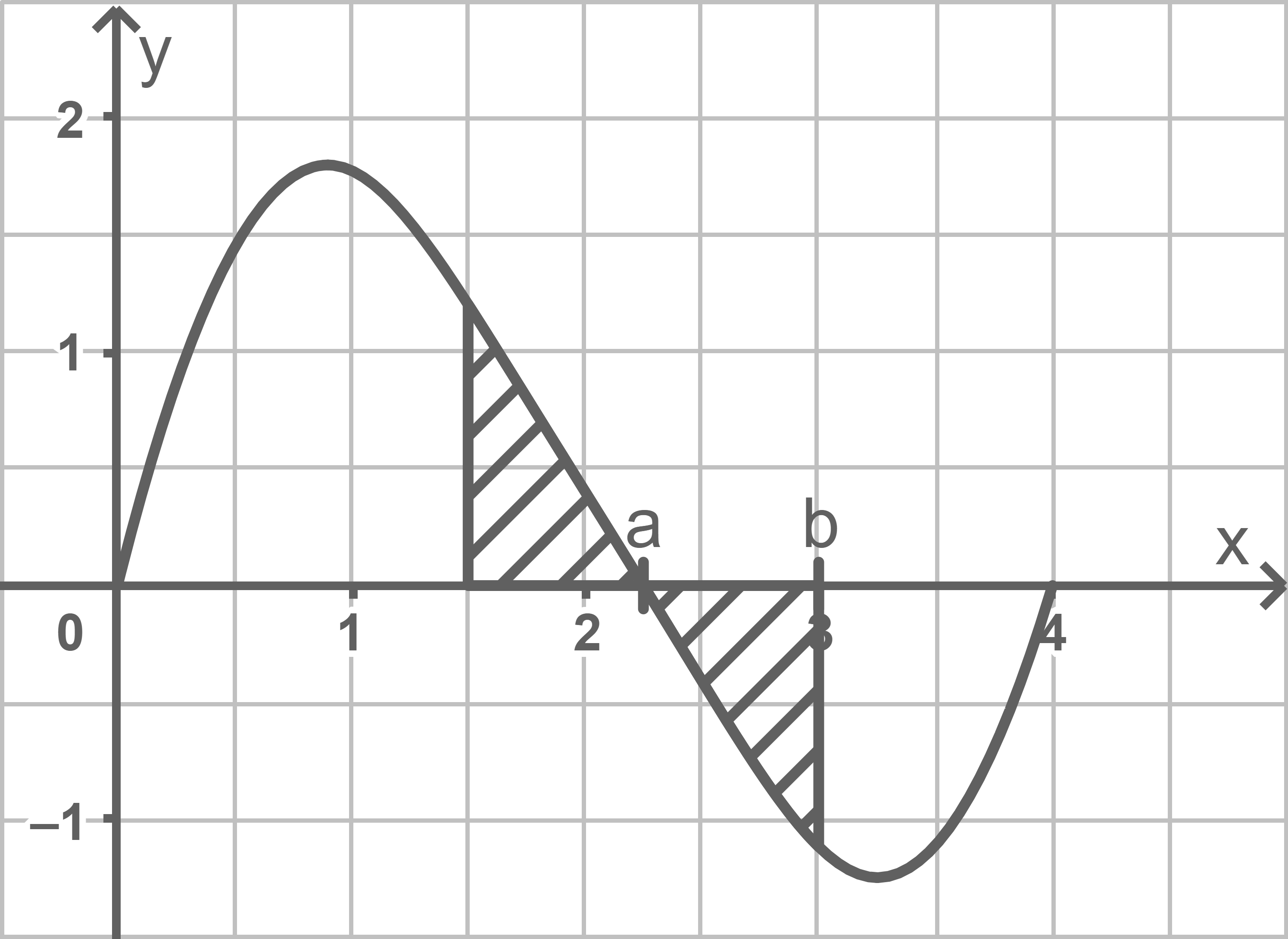
Berechne die Zunahme der Staulänge von 06:30 Uhr bis 08:00 Uhr und bestimme für diesen Zeitraum die durchschnittliche Änderungsrate der Staulänge.

(3 P)

b3)

Bestimme denjenigen Zeitpunkt zwischen 07:00 Uhr und 10:00 Uhr, zu dem die Staulänge $0,5 \;\text{km}$ geringer ist als eine Stunde vorher.

(3 P)

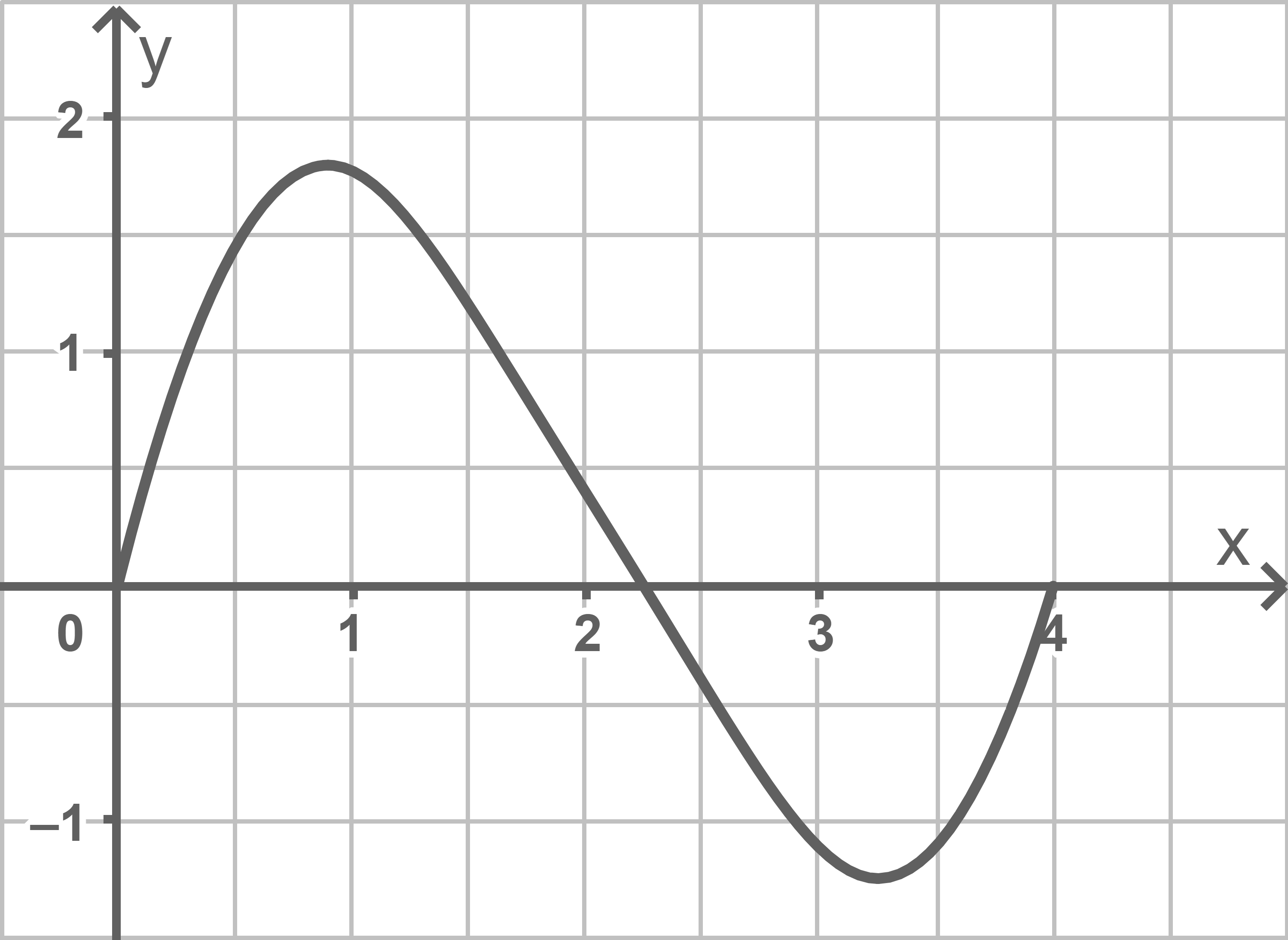
Für einen anderen Tag wird die momentane Änderungsrate der Staulänge für den Zeitraum von 6:00 Uhr bis 10:00 Uhr durch den in der Abbildung 1 gezeigten Graphen dargestellt.

Dabei gibt $x$ wieder die nach 6:00 Uhr vergangene Zeit in Stunden und $y$ die momentane Änderungsrate der Staulänge in Kilometer pro Stunde an.

Abbildung 1

c1)

Der Stau entsteht erneut um 6:00 Uhr, löst sich aber bis 10:00 Uhr nicht vollständig auf.
Begründe anhand von Abbildung 1, dass es einen Zeitpunkt gibt, an dem die Staulänge größer als 2 Kilometer ist.

(3 P)

c2)

Um 07:30 Uhr hat der Stau eine bestimmte Länge. Es gibt einen anderen Zeitpunkt, zu dem der Stau die gleiche Länge hat.
Markiere diesen Zeitpunkt in der Abbildung 1, begründe deine Markierung und veranschauliche deine Begründung in der Abbildung 1.

(3 P)

Betrachtet wird die Schar der in $\mathbb{R}$ definierten Funktionen $h_k$ mit

$h_k(x)=(x-3)^k+1$ und $k \in \mathbb{N} \setminus\{0\}.$

Die erste Ableitungsfunktion von $h_k$ wird mit $\(h_k$ bezeichnet.

d1)

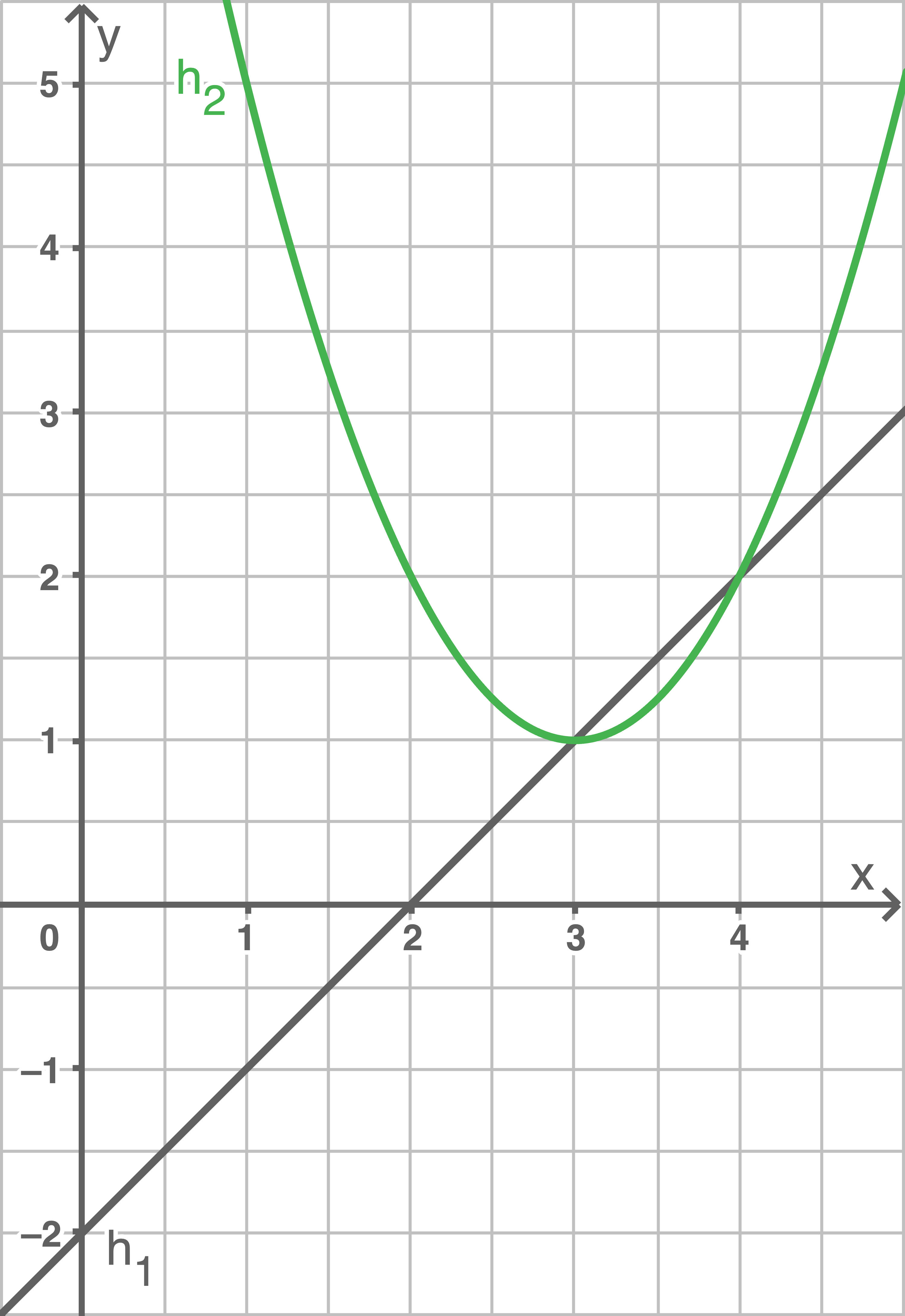
Skizziere die Graphen von $h_1$ und $h_2$ in einem gemeinsamen Koordinatensystem.

(3 P)

d2)

Untersuche, für welche Werte von $k$ die Funktion $h_k$ eine Nullstelle besitzt.

(2 P)

d3)

Beurteile die folgende Aussage:

Es gibt genau einen Wert von $k,$ für den der Graph von $\(h_k$ eine Tangente an den Graphen von $h_k$ ist.

(4 P)

d4)

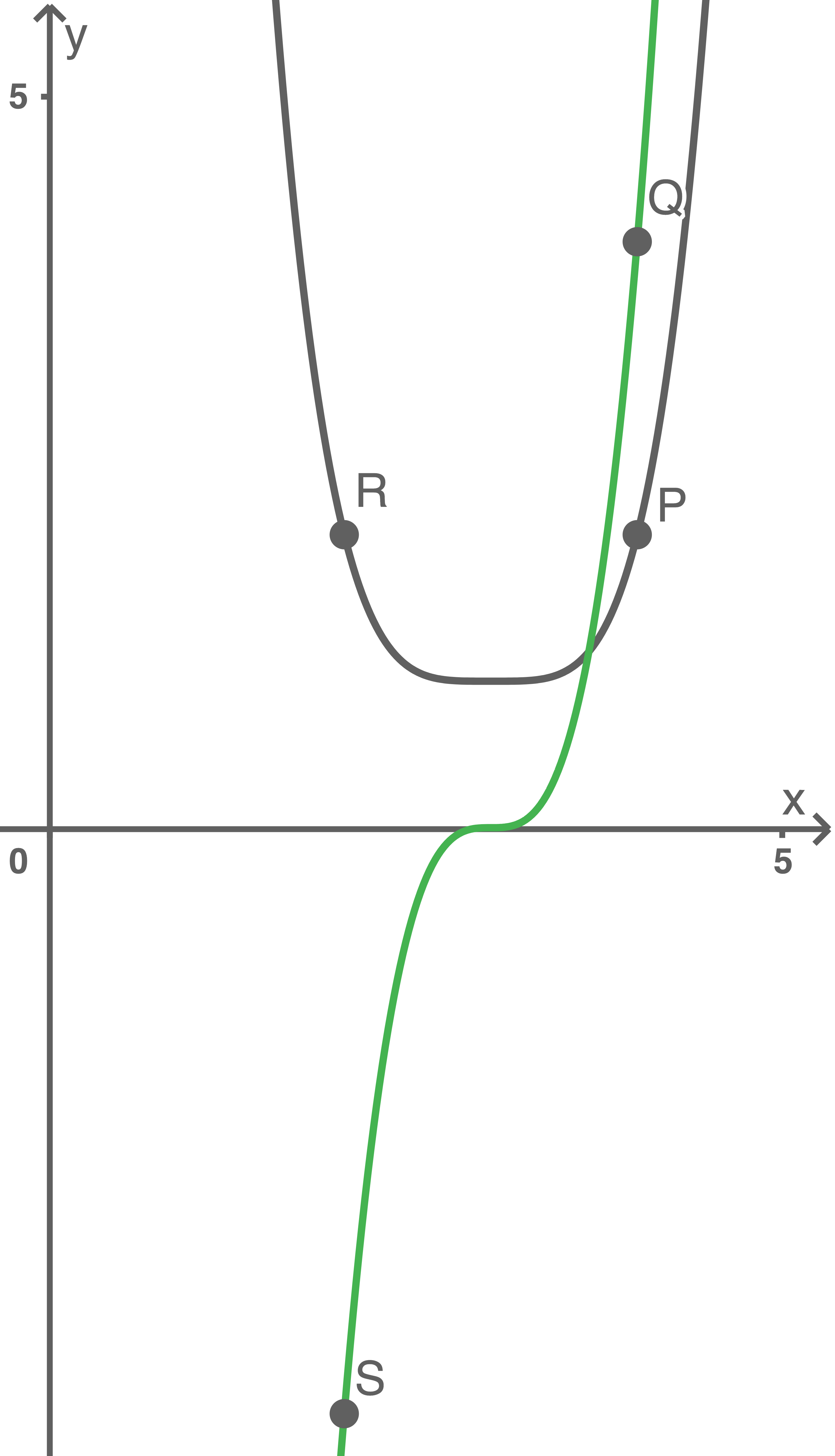
Die Graphen von $h_k$ und $\(h_k$ werden in der Abbildung 2 für $k=4$ beispielhaft für gerade Werte von $k$ gezeigt.
Für jeden geraden Wert von $k$ mit $k \geq 4$ werden die Punkte

$P\left(4 \mid h_k(4)\right),$ $Q\left(4 \mid h_k^{\prime}(4)\right),$ $R\left(2 \mid h_k(2)\right)$ und $S\left(2 \mid h_k^{\prime}(2)\right)$

betrachtet. Diese Punkte sind jeweils Eckpunkte eines Vierecks.
Begründe, dass jedes dieser Vierecke ein Trapez ist.
Beweise, dass jedes dieser Trapeze den Flächeninhalt $2k$ besitzt.

Abbildung 2

(6 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

Aus $f(x)=0$ folgt:

$x_1=0,$ $x_2=1,6$ und $x_3=4$

Dies entspricht den Zeitpunkten 06:00 Uhr, 07:36 Uhr und 10:00 Uhr.

a2)

Um 08:00 Uhr nimmt die Staulänge ab.

a3)

Zeitpunkt mit der stärksten Zunahme berechnen

Mit dem notwendigen Kriterium für Extremstellen und dem CAS folgt:

$\(\begin{array}[t]{rll} f$

Ein Vergleich der Funktionswerte an den infragekommenden Extremstellen liefert:

$f(0,62) \approx 2,17$

$f(2,58) \approx -1,59$

$f(4) = 0$

$f(0) = 0$

Die Staulänge nimmt also ca. 0,62 Stunden nach 06:00 Uhr am stärksten zu.

$0,62\cdot 60 = 37,2\;[\text{min}]$

Um ca. 06:37 Uhr nimmt die Staulänge am stärksten zu.

a4)

Der Stau ist um 07:36 Uhr am längsten.

Die Länge des Staus nimmt genau dann zu, wenn $f(x) \gt 0.$
Dies ist zwischen der ersten und zweiten Nullstelle der Fall. Bis 07:36 Uhr nimmt die Staulänge daher zu und ab 07:36 Uhr bis 10:00 Uhr nimmt sie dann wieder ab.

b1)

Die Funktion $f$ modelliert die Änderungsrate der Staulänge im Zeitraum von 06:00 Uhr bis 10:00 Uhr. Die Staulänge wird also durch die Stammfunktion von $f$ beschrieben, die für $x=0$ den Wert null annimmt.

$\(\begin{array}[t]{rll} s$

Es gilt also $\(s$

Zudem gilt $s(0) = -\frac{1}{16}\cdot 0^5 +\frac{3}{4}\cdot 0^4 -3\cdot 0^3 +4\cdot 0^2 = 0.$

Somit kann die Staulänge zu jedem Zeitpunkt von 06:00 Uhr bis 10:00 Uhr durch die Funktion $s$ angegeben werden.

b2)

Zunahme der Staulänge berechnen

$s(2)-s(0,5)\approx 2\;[\text{km}] - 0,7\;[\text{km}]$ $= 1,3 \;[\text{km}]$

Die Länge des Staus hat zwischen 06:30 Uhr und 08:00 Uhr damit um ca. $1,3\;[\text{km}]$ zugenommen.

Durchschnittliche Änderungsrate bestimmen

$\dfrac{s(2)-s(0,5)}{2-0,5} \approx\frac{1,3\;\text{km}}{1,5\;\text{h}} \approx 0,9\frac{\text{km}}{\text{h}}.$

b3)

Gesucht ist der Zeitpunkt $x$ mit $s(x)=s(x-1)-0,5.$

Eingabe dieser Gleichung in den CAS und nach $x$ auflösen liefert im Intervall $[1;4]:$

$x_2\approx 2,32$

Mit $0,32\cdot60=19,2 \;[\text{min}]$ ist der gesuchte Zeitpunkt ca. 08:19 Uhr.

c1)

Der Inhalt der Fläche, die der Graph mit der $x$ -Achse im Bereich $0\leq x \leq 2,2$ einschließt, entspricht der Länge in Kilometer, um die der Stau in den ersten $2,2$ Stunden wächst.

Der Abbildung lässt sich durch Zählen der Kästchen entnehmen, dass diese Fläche größer als $2\,\text{FE}$ ist. Der Stau nimmt in den ersten 2,2 Stunden also um mehr als $2\,\text{km}$ zu und ist somit zu einem Zeitpunkt größer als $2\,\text{km}.$

c2)

Die Länge des Staus wird durch den Inhalt der Fläche, die der Graph im Intervall $[0;b]$ mit der $x$ -Achse einschließt, beschrieben. Ist der Flächeninhalt der Flächen, die der Graph mit der $x$ -Achse für $1,5\leq x\leq a$ oberhalb der $x$ -Achse und $a\leq x \leq b$ unterhalb der $x$ -Achse einschließt, gleich groß, so entspricht $b$ dem gesuchten Zeitpunkt.

d1)

Graphenschar - Schleswig-Holstein Abi 2023

d2)

$\begin{array}[t]{rll} h_k(x) &=& 0 \\[5pt] (x-3)^k +1 &=& 0 &\quad \scriptsize \mid\; -1 \\[5pt] (x-3)^k &=& -1 \end{array}$

Die Gleichung kann nur für ungerade Werte von $k$ erfüllt werden. Dann muss zudem $x-3 =-1$ gelten, also $x=2.$

Die Funktion $h_k$ besitzt nur für ungerade $k$ eine Nullstelle, undzwar $x=2.$

d3)

$\(h_k{ }$ $= k\cdot(x-3)^{k-1}$

Eine Tangente ist immer eine Gerade, die zugehörige Funktion also maximal vom Grad $1.$ Da $\(h_k{ }$ durch das Ableiten vom Grad $k-1$ ist, kommen nur $k=1$ und $k=2$ infrage.

Für $k=1$ handelt es sich bei dem Graphen von $h_k$ allerdings um eine Gerade, die keine Tangente besitzen kann. Also bleibt nur $k=2$ zu überprüfen.

1. Schritt: Funktionswerte von $h_2$ und $\(h_2{ }$ vergleichen

Rechenweg anzeigen

$x=4$

2. Schritt: Steigungen vergleichen

Die Steigung von $\(h_2$ lässt sich zu $m=2$ aus der Funktionsgleichung ablesen.

Außerdem ergibt sich die Steigung des Graphen von $h_2$ an der Stelle $x=4$ zu:

$\(h_2$

An der Stelle $x=4$ besitzen die Graphen von $h_2$ und $\(h_2$ also einen gemeinsamen Punkt mit identischer Steigung.

Damit ist die Aussage aus der Aufgabenstellung korrekt.

d4)

Trapezform begründen

Die Punkte $P$ und $Q,$ sowie die Punkte $R$ und $S$ haben jeweils übereinstimmende $x$ -Koordinaten. Damit sind die Seiten $\overline{PQ}$ und $\overline{RS}$ parallel.

Flächeninhalt beweisen

Die Höhe der Trapeze beträgt in jedem Fall $h=4-2 = 2.$

Bei geradem $k$ folgt für die Flächeninhalte der Trapeze damit:

Rechenweg anzeigen

$\begin{array}[t]{rll} A_{k}&=& 2\cdot\dfrac{\vert\overline{PQ}\vert+\vert\overline{RS}\vert}{2} \\[5pt] & ... & \\[5pt] &=& 2k \;[\text{FE}] \\[10pt] \end{array}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?