Analysis 2

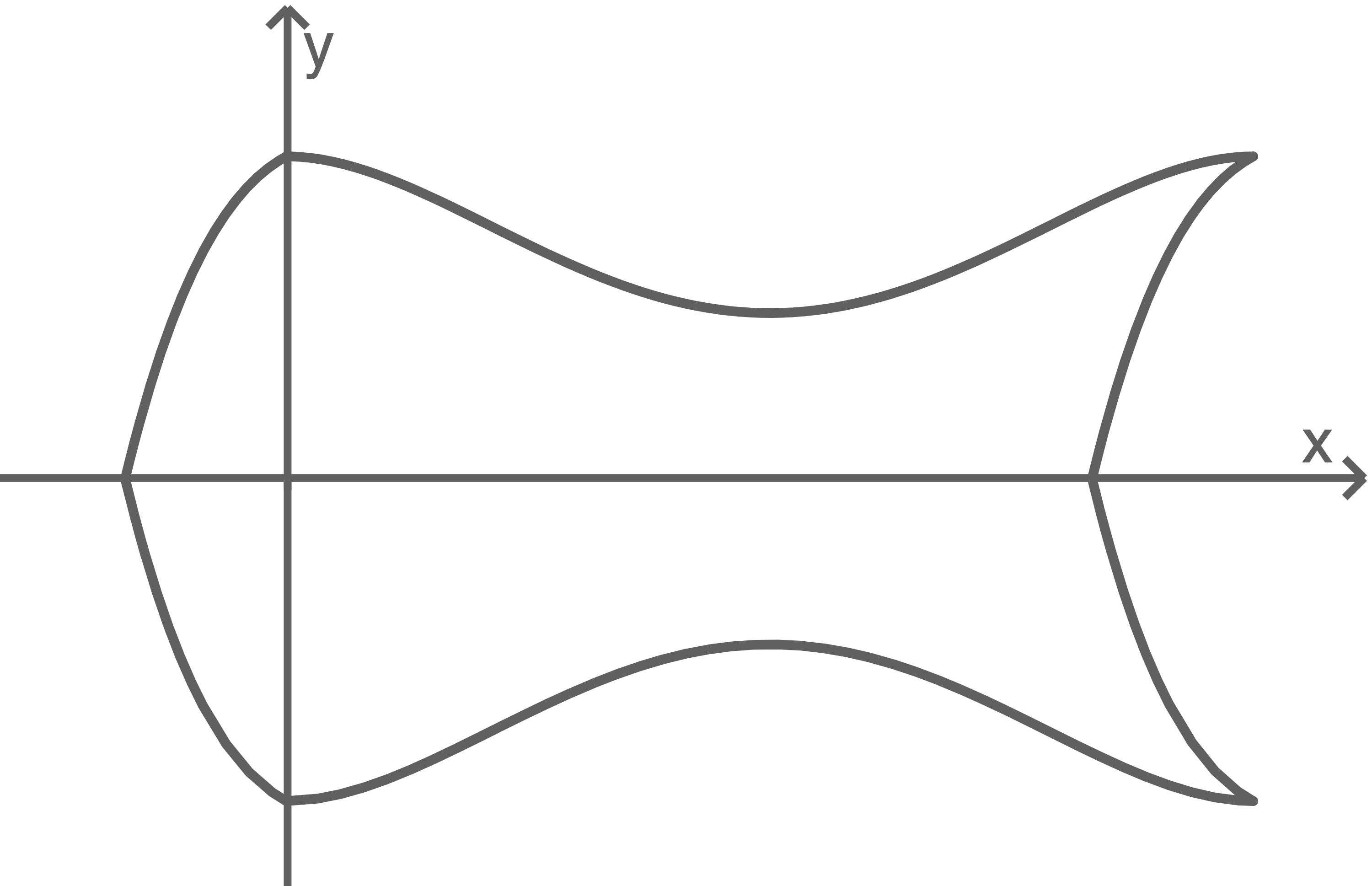
Eine dekorativ geschwungene Gehwegplatte wird untersucht. Wird die Gehwegplatte von oben betrachtet, hat sie die in der Abbildung dargestellte Form. Diese Form ist symmetrisch bezüglich der $x$ -Achse des eingezeichneten Koordinatensystems.

Der obere Rand der Form wird beschrieben mithilfe des Graphen der Funktion $f$ mit

$f(x)$ $=-\frac{3}{250} \cdot x^{4}+\frac{18}{125} \cdot x^{3}-\frac{54}{125} \cdot x^{2}+2$ und $0 \leq x \leq 6$

Eine Längeneinheit entspricht einem Dezimeter in der Wirklichkeit.

a1)

Berechne die Koordinaten des Tiefpunktes des Graphen von $f.$

(4 P)

a2)

Zeichne den Graphen von $f$ in die Abbildung 1 auf dem Beiblatt.

(3 P)

a3)

Die Breite der Form an jeder Stelle $x$ mit $x \in[0 ; 6]$ ist $2 \cdot f(x).$ Es gibt zwei Stellen $x \in[0 ; 6],$ an denen die Form eine Breite von 3 Längeneinheiten aufweist.

Bestimme den Abstand dieser beiden Stellen voneinander.

(3 P)

Der linke Rand der Form wird oberhalb der $x$ -Achse modelliert mithilfe des Graphen der Funktion $l$ mit

$l(x)=2 \cdot(x+1) \cdot \mathrm{e}^{-0,73 \cdot x}$ und $-1 \leq x \leq 0.$

Der rechte Rand der Form wird mithilfe einer Funktion $r$ modelliert. Der Graph von $r$ ergibt sich durch eine Verschiebung des Graphen von $l$ entlang der $x$ -Achse und ist über dem Intervall $[5 ; 6]$ in der Abbildung 1 auf dem Beiblatt dargestellt.

b1)

Leite einen Funktionsterm von $r$ her.

(2 P)

b2)

Begründe, dass der Flächeninhalt der Form mit dem Term $2 \cdot \displaystyle\int_{0}^{6} f(x)\; \mathrm{d} x$ berechnet werden kann.

(3 P)

b3)

Ein Kubikdezimeter des zur Herstellung der Gehwegplatten verwendeten Materials hat eine Masse von $1,76 \mathrm{~kg}.$

Berechne die Masse einer Gehwegplatte mit einer Plattendicke von einem halben Dezimeter.

(4 P)

b4)

Die Bogenlänge $L$ des Graphen einer differenzierbaren Funktion $h$ über einem Intervall $[a ; b]$ lässt sich berechnen durch

$L=\displaystyle\int_{a}^{b} \sqrt{1+\left(h^{\prime}(x)\right)^{2}} \mathrm{~d} x.$

Berechne mithilfe dieser Formel den Umfang der Form.

(4 P)

c1)

Der linke und der obere Rand der Form treffen im Punkt $(0 \mid 2)$ in einem Winkel $\alpha$ aufeinander. Die Situation ist in der Abbildung 2 auf dem Beiblatt dargestellt.
Berechne $\alpha.$

(3 P)

c2)

Die Gerade $g$ verläuft durch den Punkt $P(0 \mid 2)$ und ist orthogonal zur Tangente an den Graphen von $l$ im Punkt $P.$
Berechne den Schnittpunkt von $g$ mit der $x$ -Achse.

(4 P)

Betrachtet wird nun die Schar der in $\mathbb{R}$ definierten Funktionen $f_{k}$ mit

$f_{k}(x)$ $=-\frac{1}{100} k \cdot x^{4}+\frac{3}{25} k \cdot x^{3}-\frac{9}{25} k \cdot x^{2}+2$ und $k \neq 0.$

d1)

Berechne den Wert $k,$ für den $f_{k}(x)=f(x)$ ist.

(2 P)

d2)

Bestimme für jedes $k \neq 0$ die Wendestellen von $f_{k}.$

$[$ Kontrolle: $x=-\sqrt{3}+3 \vee x=\sqrt{3}+3]$

(4 P)

d3)

Die Wendepunkte der Graphen der Funktionen $f_{k}$ liegen oberhalb, unterhalb bzw. auf der $x$ -Achse.

Untersuche diesbezüglich die Lage der Wendepunkte in Abhängigkeit von $k.$

(4 P)

Material (Beiblatt)

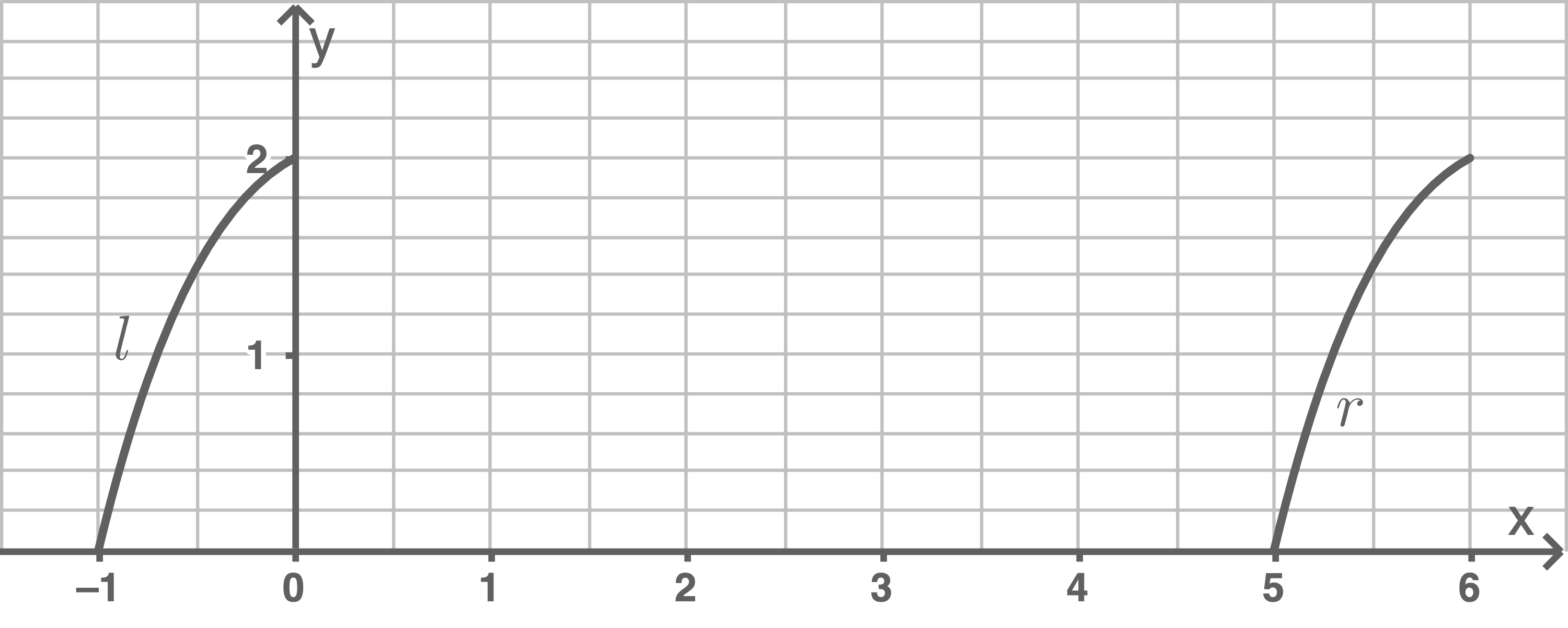
Gehwegplatte Beiblatt - Schleswig-Holstein Abi CAS 2022 (Analysis 2)

Abbildung 1

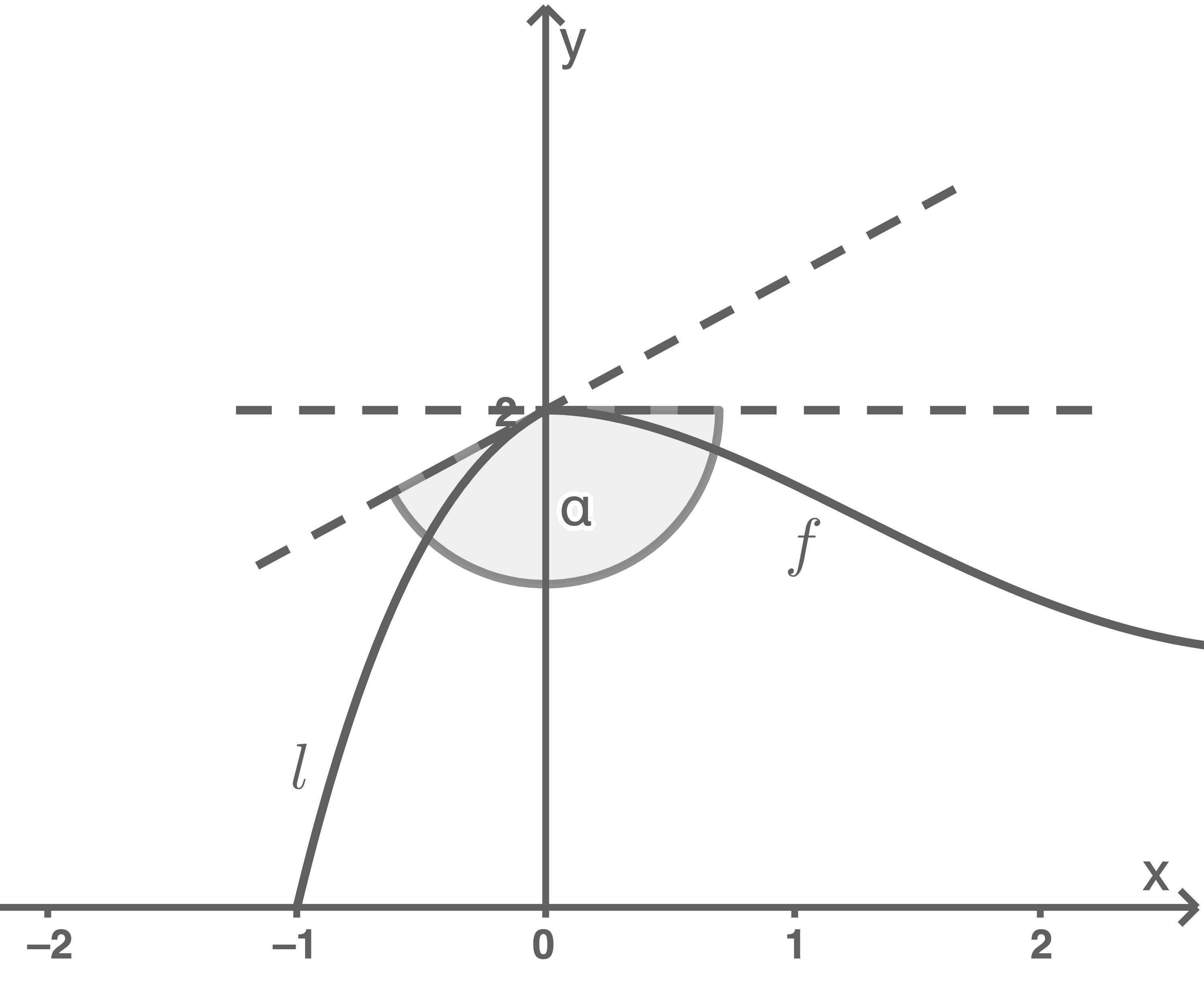
Winkel Gehwegplatte - Schleswig-Holstein Abi CAS 2022 (Analysis 2)

Abbildung 2

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

Mit dem notwendigen Kriterium für eine Extremstelle $x$ mit $0 \leq x\leq 6$ von $f$ muss $f^{\prime}(x)=0$ gelten.
Mit dem Ableitungs- und solve-Befehl des CAS ergeben sich die Lösungen der Gleichung $\(f$ zu $x_1 = 0,$ $x_2=3$ und $x_3=6.$

Zusätzlich folgt mit dem CAS für das hinreichende Kriterium:

$f^{\prime \prime}(3)=\frac{54}{125}>0$

Für die $y$ -Koordinate gilt $f(3)=1,028.$

An der Stelle $3$ befindet sich also der Tiefpunkt mit den Koordinaten $(3 \mid 1,028).$

a2)

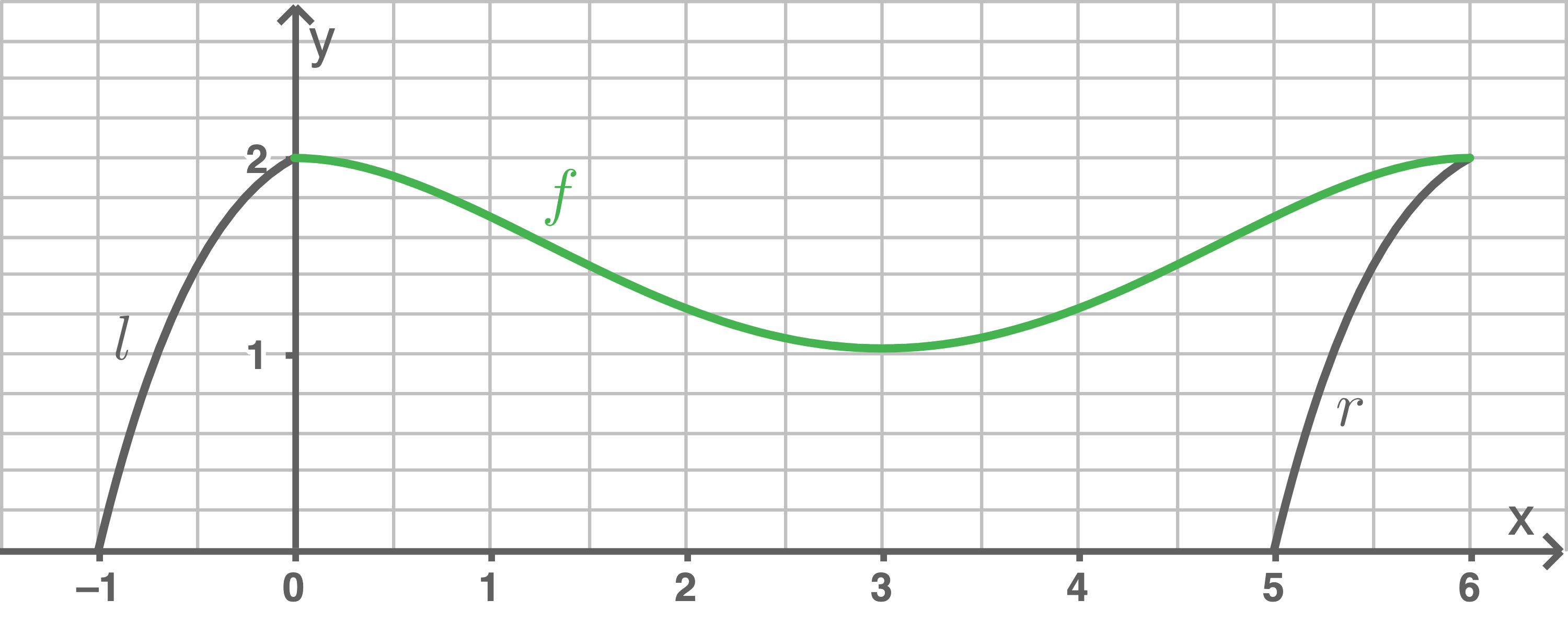
Graph - Schleswig-Holstein Abi CAS 2022 (Analysis 2)

a3)

$2 \cdot f(x)=3$ ergibt mit dem solve-Befehl des CAS die Lösungen $x_1 \approx 1,4047$ und $x_2 \approx 4,5953.$

Wegen $4,5953-1,4047 = 3,1906$ liegen die Stellen etwa $3,19\,\text{LE} = 3,19\,\text{dm}$ voneinander entfernt.

b1)

Der Graph von $r$ ergibt sich durch Verschiebung des Graphen von $l$ um 6 Längeneinheiten nach rechts:

$r(x)=l(x-6)$ $=2 \cdot(x-6+1) \cdot \mathrm{e}^{-0,73 \cdot(x-6)}$ $= 2 \cdot(x-5) \cdot \mathrm{e}^{-0,73 \cdot(x-6)}$

b2)

Aufgrund der Symmetrie der Form bezüglich der $x$ -Achse gilt für ihren Flächeninhalt

Rechenweg anzeigen

$A=...$

Da der Graph von $r$ durch eine Verschiebung des Graphen von $l$ entstanden ist, gilt

$\displaystyle\int_{-1}^{0} l(x)\; \mathrm{d}x=\displaystyle\int_{5}^{6} r(x) \;\mathrm{d} x.$

Damit gilt insgesamt:

Rechenweg anzeigen

$A=2 \cdot \displaystyle\int_{0}^{6} f(x)\; \mathrm{d} x$

b3)

Mit dem CAS lässt sich der Flächeninhalt der Form berechnen:

$A=2 \cdot \displaystyle\int_{0}^{6} f(x) \mathrm{d} x \approx 17,78$

Für das Volumen der Gehwegplatte folgt:

$V \approx 17,78\,\text{dm}^{2} \cdot 0,5\,\text{dm}=8,89\,\text{dm}^{3}$

Die Masse ist dann:

$8,89\,\text{dm}^{3} \cdot 1,76\, \frac{\text{kg}}{\text{dm}^{3}} \approx 15,65 \,\text{kg}$

b4)

Mithilfe der Formel und dem CAS ergibt sich für den Umfang $U$ der Form

Rechenweg anzeigen

$U\approx 21,89\,\text{[LE]}$

Der Umfang der Form beträgt ca. $21,89\,\text{dm}.$

c1)

$\alpha$ ist der größere der beiden Winkel, die die Tangenten an die Graphen von $l$ und $f$ im Punkt $P$ einschließen.
Der kleinere wird mit $\alpha_1$ bezeichnet.

Die Steigungen der beiden Tangenten sind $\(f$ und $\(l$

Wegen $f^{\prime}(0)=0$ ist $l^{\prime}(0)=\tan \left(\alpha_{1}\right).$

$\alpha=180^{\circ}-\alpha_{1}=180^{\circ}-\tan^{-1} \left(l^{\prime}(0)\right)$ $=180^{\circ}-\tan^{-1} \left(\frac{27}{50}\right) \approx 151,63^{\circ}$

c2)

Die Steigung von $g$ ergibt sich aus der Steigung der Tangente an den Graphen von $l$ im Punkt $P$ zu:

$\(m_g = -\dfrac{1}{m_t} = -\dfrac{1}{l$

Der $y$ -Achsenabschnitt ist $l(0)=2.$

Die Gerade $g$ kann daher durch die Gleichung

$g(x)=-\frac{1}{l^{\prime}(0)} \cdot x+l(0)=-\frac{50}{27} \cdot x+2$

beschrieben werden.

Die Schnittstelle mit der $x$ -Achse ist die Lösung der Gleichung $g(x)=0,$ die mit dem CAS berechnet wird: $x=\frac{27}{25}.$

Der Schnittpunkt von $g$ mit der $x$ -Achse hat damit die Koordinaten $\left(\frac{27}{25} \mid 0\right).$

d1)

Es ist $k$ mit $f_k(x)= f(x)$ gesucht. Durch den Vergleich eines der Koeffizienten ergibt sich beispielsweise:

$\begin{array}[t]{rll} -\frac{1}{100}\cdot k &=& -\frac{3}{250} &\quad \scriptsize \mid\;\cdot (-100) \\[5pt] k &=& \frac{6}{5} = 1,2 \end{array}$

d2)

Mit dem notwendigen Kriterium für eine Wendestelle $x$ von $f_{k}$ muss $f_{k}^{\prime \prime}(x)=0$ sein.

Mit dem CAS ergeben sich die Lösungen dieser Gleichung:

$x_1=-\sqrt{3}+3$ und $x_2=\sqrt{3}+3$

Für das hinreichende Kriterium für Wendestellen folgt ebenfalls mit dem CAS:

$f_{k}^{\prime \prime \prime}(-\sqrt{3}+3)=\frac{6 \cdot k \cdot \sqrt{3}}{25} \neq 0$

$f_{k}^{\prime \prime \prime}(\sqrt{3}+3)=\frac{-6 \cdot k \cdot \sqrt{3}}{25} \neq 0$

Also sind die Stellen $-\sqrt{3}+3$ und $\sqrt{3}+3$ die Wendestellen von $f_{k}.$

d3)

Die Lage der Wendepunkte bezüglich der $x$ -Achse wird durch die $y$ -Koordinate beschrieben.

$f_{k}(-\sqrt{3}+3)=2-\frac{9 \cdot k}{25}$

$f_{k}(\sqrt{3}+3) = 2-\frac{9 \cdot k}{25}$

Die Wendepunkte haben also die Koordinaten $\left(-\sqrt{3}+3 \mid 2-\frac{9 \cdot k}{25}\right)$ und $\left(\sqrt{3}+3 \mid 2-\frac{9 \cdot k}{25}\right).$

Mit dem CAS lassen sich folgende Ungleichungen lösen:

$2-\frac{9 \cdot k}{25}\lt 0$ gilt für $k\gt\frac{50}{9},$ sodass beide Wendepunkte des Graphen von $f_{k}$ für $k\gt\frac{50}{9}$ unterhalb der $x$ -Achse liegen.

$2-\frac{9 \cdot k}{25}=0$ gilt für $k=\frac{50}{9},$ sodass beide Wendepunkte des Graphen von $f_{k}$ für $k=\frac{50}{9}$ auf der $x$ -Achse und für $k\lt\frac{50}{9}$ oberhalb der $x$ -Achse liegen.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?