Analytische Geometrie 2
An einem Balkon wird ein Solarmodul montiert. In einem geeigneten Koordinatensystem beschreibt die  -Ebene den Erdboden. Das Viereck
-Ebene den Erdboden. Das Viereck  mit den Eckpunkten
mit den Eckpunkten 
 und
und  liegt in einer Ebene
liegt in einer Ebene  und beschreibt die Moduloberseite. Eine Längeneinheit entspricht einem Meter in der Wirklichkeit.
und beschreibt die Moduloberseite. Eine Längeneinheit entspricht einem Meter in der Wirklichkeit.
a)
a1)
Weise nach, dass das Viereck  ein Rechteck ist.
ein Rechteck ist.
(3 BE)
a2)
Berechne den Flächeninhalt der Moduloberseite und die Länge einer Diagonalen.
(4 BE)
a3)
Bestimme eine Gleichung der Ebene  in Koordinatenform.
in Koordinatenform.
[zur Kontrolle: ]
]
[zur Kontrolle:
(3 BE)
a4)
Jede Gerade, die in der Ebene  liegt und durch das Innere des Rechtecks
liegt und durch das Innere des Rechtecks  verläuft, teilt das Rechteck in genau zwei Vielecke: ein
verläuft, teilt das Rechteck in genau zwei Vielecke: ein  -Eck und ein
-Eck und ein  -Eck.
Gib alle möglichen Paare
-Eck.
Gib alle möglichen Paare  mit
mit  an.
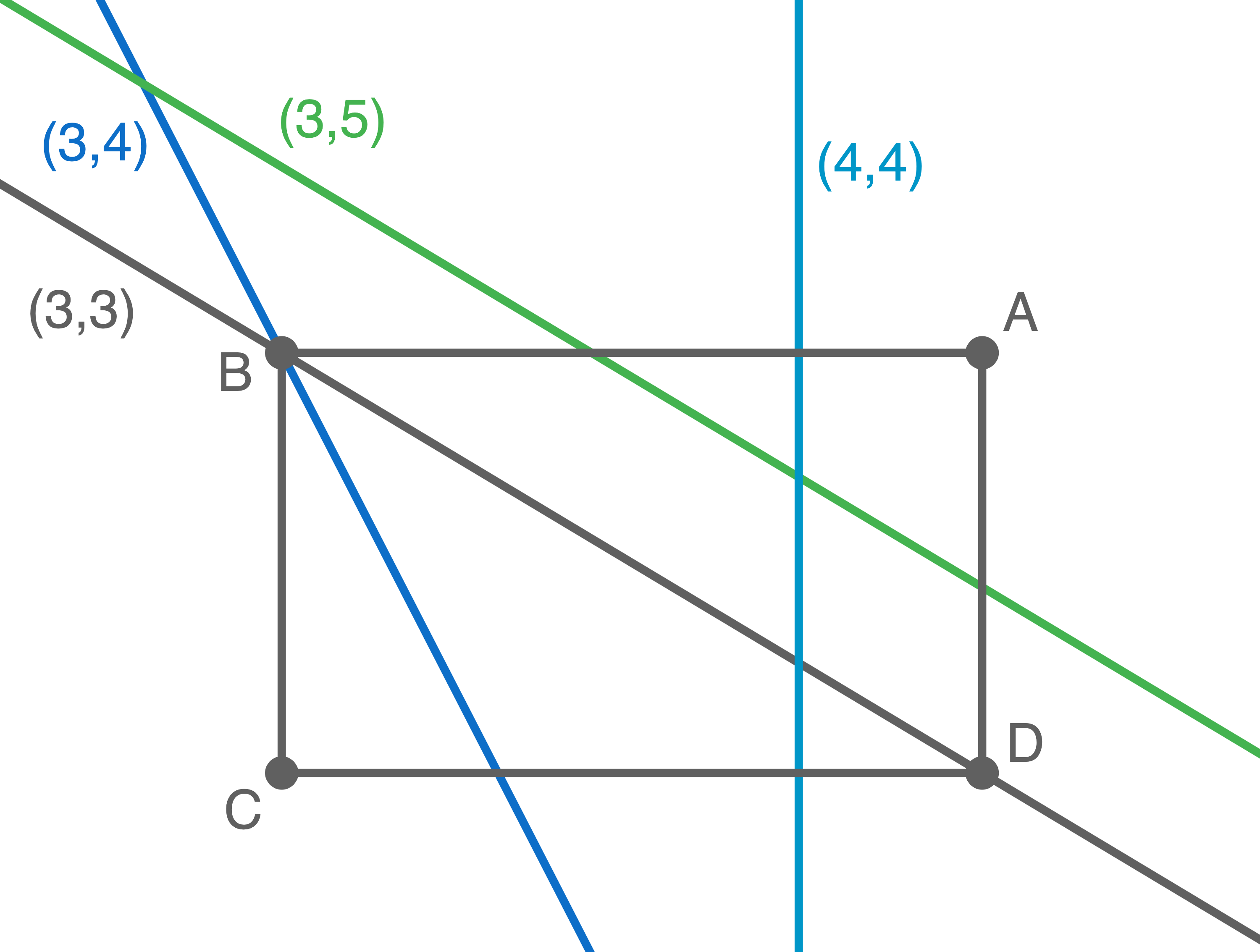
Skizziere für jedes dieser Paare beispielhaft eine Gerade in die folgende Abbildung.
an.
Skizziere für jedes dieser Paare beispielhaft eine Gerade in die folgende Abbildung.


(4 BE)
b)
Der Punkt  stellt die Spitze eines Fahnenmastes in der Nähe des Balkons dar. Zu einem bestimmten Zeitpunkt verlaufen die Sonnenstrahlen in eine Richtung, die durch den Vektor
stellt die Spitze eines Fahnenmastes in der Nähe des Balkons dar. Zu einem bestimmten Zeitpunkt verlaufen die Sonnenstrahlen in eine Richtung, die durch den Vektor  beschrieben wird. Die Spitze des Fahnenmastes erzeugt dabei auf der Moduloberseite einen Schattenpunkt, der im Modell durch den Punkt
beschrieben wird. Die Spitze des Fahnenmastes erzeugt dabei auf der Moduloberseite einen Schattenpunkt, der im Modell durch den Punkt  dargestellt wird.
dargestellt wird.
b1)
Berechne die Koordinaten von 
(4 BE)
b2)
Berechne die Größe des Schnittwinkels der Gerade durch die Punkte  und
und  mit der Ebene
mit der Ebene 
(3 BE)
b3)
Nun wird die Richtung der Sonnenstrahlen allgemeiner durch den Vektor  mit
mit  beschrieben.
Mit Hilfe eines Normalenvektors
beschrieben.
Mit Hilfe eines Normalenvektors  der Ebene
der Ebene  wird die Funktion
wird die Funktion  mit
mit

 für
für  definiert. Die Funktion
definiert. Die Funktion  hat genau eine Maximalstelle
hat genau eine Maximalstelle  Es gilt
Es gilt  Berechne
Berechne  mit
mit  und
und  Erläutere die Bedeutung von
Erläutere die Bedeutung von  im Sachzusammenhang.
im Sachzusammenhang.
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a)
a1)
a2)
Flächeninhalt berechnen

 Der Flächeninhalt der Moduloberseite beträgt damit
Der Flächeninhalt der Moduloberseite beträgt damit  Länge einer Diagonalen berechnen
Länge einer Diagonalen berechnen
 Für die Länge der Diagonale
Für die Länge der Diagonale  gilt:
gilt:
 Die Diagonale ist somit ca.
Die Diagonale ist somit ca.  lang.
lang.
a3)
a4)
Es treten folgende Paare  auf:
auf:  und
und 

b)
b1)
Die Gerade  verläuft durch den Punkt
verläuft durch den Punkt  in Richtung des Vektors
in Richtung des Vektors  und wird somit durch folgende Gleichung beschrieben:
und wird somit durch folgende Gleichung beschrieben:
 Um den Schnittpunkt von
Um den Schnittpunkt von  mit der Ebene
mit der Ebene  der Moduloberseite zu finden, werden die allgemeinen Koordinaten eines Punktes auf der Geraden
der Moduloberseite zu finden, werden die allgemeinen Koordinaten eines Punktes auf der Geraden  in die Koordinatengleichung von
in die Koordinatengleichung von  eingesetzt:
Es folgt:
eingesetzt:
Es folgt:
 Der Punkt
Der Punkt  hat somit die Koordinaten
hat somit die Koordinaten 
b2)
Der Schnittwinkel  der Geraden
der Geraden  und der Ebene
und der Ebene  wird durch den Winkel zwischen dem Richtungsvektor
wird durch den Winkel zwischen dem Richtungsvektor  der Geraden und dem Normalenvektor
der Geraden und dem Normalenvektor  der Ebene bestimmt.
Der Schnittwinkel lässt sich wie folgt berechnen:
der Ebene bestimmt.
Der Schnittwinkel lässt sich wie folgt berechnen:
b3)
Daraus folgt:
![\(\begin{array}[t]{rll}
\sin(\alpha)&=& f(k^*) \\[5pt]
\sin(\alpha)&=& f(1,64) \\[5pt]
\sin(\alpha)&\approx& 0,814 \quad \scriptsize \mid\;\sin^{-1} \\[5pt]
\alpha &\approx& 54,5^\circ
\end{array}\)](https://mathjax.schullv.de/baa2f5c5c0385400a7fd6eef2022ac60e026d6f2ae1508d2f5d666921b57b9cf?color=5a5a5a) Im Sachzusammenhang ist
Im Sachzusammenhang ist  die Größe des maximalen Winkels, unter dem die Sonnenstrahlen auf die Moduloberseite treffen.
die Größe des maximalen Winkels, unter dem die Sonnenstrahlen auf die Moduloberseite treffen.