Analysis 1

Im Jahr 2019 zerstörte ein Großbrand das Dach der Kathedrale Notre-Dame de Paris. Eine der vielen Ideen für den geplanten Wiederaufbau sieht die Errichtung eines Glasdachs mit einem gläsernen Turm darauf vor.

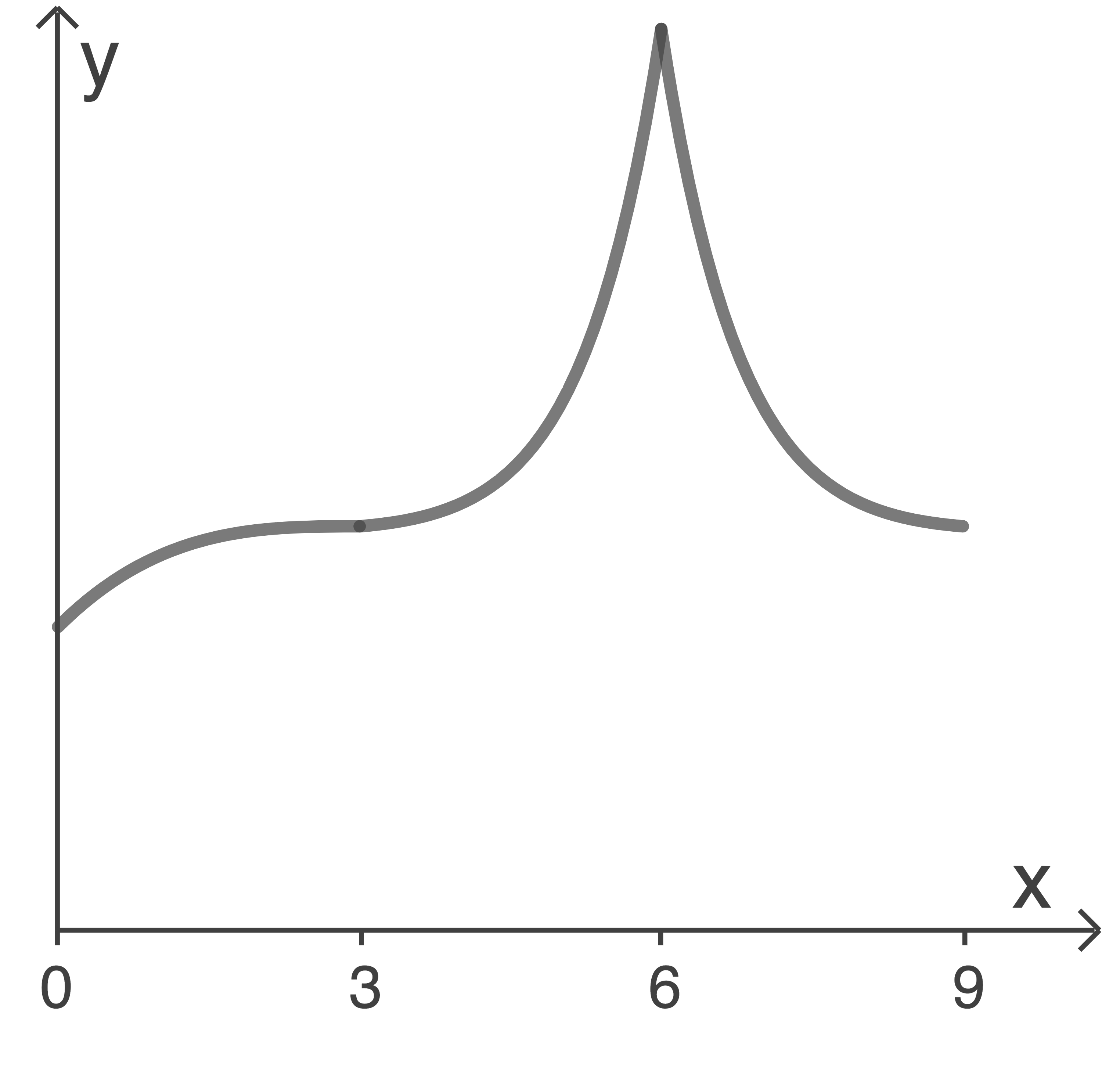
Graph mit einer Kurve, die die Beziehung zwischen den Variablen x und y darstellt.

Skizze eines historischen Gebäudes mit spitzem Turm und dekorativer Fassade.

In einem geeigneten Koordinatensystem wird der Dachfirst mit Hilfe von Funktionsgraphen modelliert. Die Funktionswerte geben die Höhe des Dachfirsts über dem Boden an; die $x$ -Achse beschreibt das Bodenniveau. Dabei entspricht eine Längeneinheit 10 m in der Wirklichkeit.

Zunächst wird eine ganzrationale Funktion $f$ dritten Grades betrachtet. Der Graph von $f$ verläuft durch die beiden Punkte $P(O \mid 3)$ und $W(3 \mid 4)$ . Dabei ist $W$ ein Wendepunkt mit waagerechter Tangente. Mit Hilfe des Graphen von $f$ wird über dem Intervall $[0;3]$ ein erstes Teilstück des Dachfirsts modelliert.

a1)

Leite einen Funktionsterm von $f$ her.

[Kontrolle: $f(x)=\dfrac{1}{27}x^3-\dfrac{1}{3}x^2+x+3$ ]

(6 P)

a2)

Berechne die Höhe des Dachfirsts über dem Boden an der Stelle $x = 1$ .

(2 P)

a3)

Gib einen Funktionsterm der Ableitungsfunktion $\(f$ und die Steigung des Graphen von $f$ an der Stelle $x = 0$ an.

(2 P)

a4)

Weise mit Hilfe einer Rechnung nach, dass der Graph von $f$ für $x \lt 3$ rechtsgekrümmt ist.

(3 P)

Nun werden eine Funktion $g$ und ihre Ableitungsfunktion $\(g$ mit

$g(x)= (x-3)\cdot \mathrm{e}^{x-5,5}+4$ und $\(g$

betrachtet. Mit Hilfe des Graphen von $g$ wird über dem Intervall $[3;6]$ ein weiteres Teilstück des Dachfirsts modelliert.

b1)

Ergänze die Wertetabelle zu $g$ , und zeichne den Graphen von $g$ über dem Intervall $[3;6]$ in das vorgegebene Koordinatensystem.

$x$	$g(x)$
$3$	$4,00$
$3,5$
$4$	$4,22$
$4,5$
$5$
$5,5$	$6,50$
$6$

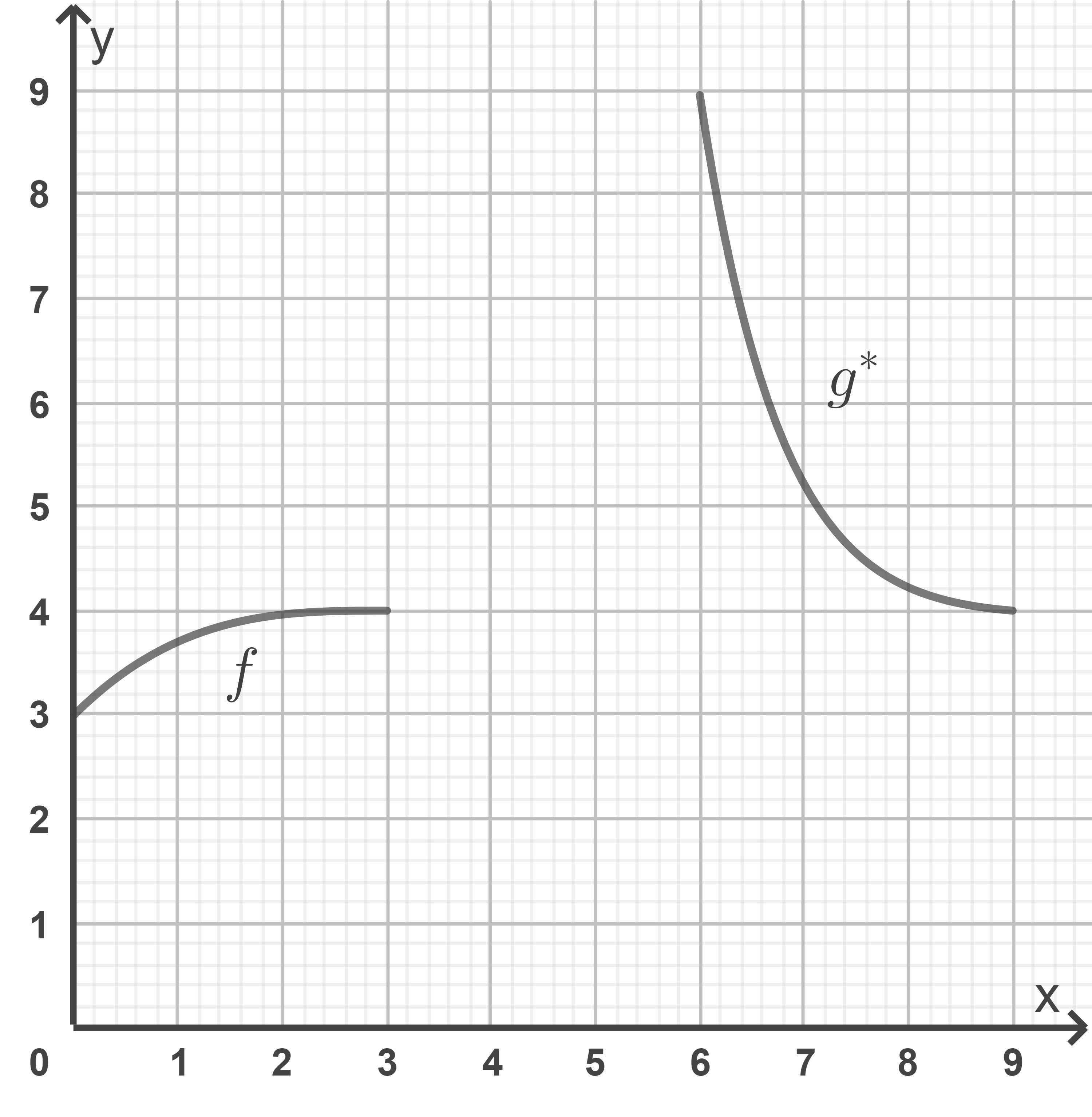
Diagramm mit zwei Funktionen f und g* auf einem Koordinatensystem. X- und Y-Achse sind beschriftet.

(4 P)

b2)

Die Graphen von $f$ und $g$ verlaufen beide durch den Punkt $W(3 \mid 4)$ .
Prüfe, ob der Dachfirst dort knickfrei modelliert wird.

(3 P)

b3)

Bestimme alle Extrem- und Wendestellen der auf ganz $\mathbb{R}$ definierten Funktion $g$ .

(8 P)

b4)

Der Graph der Funktion $g$ wird an der $y$ -Achse gespiegelt und dann um zwölf Längeneinheiten nach rechts verschoben. Dadurch ergibt sich der Graph der Funktion $g^*$ , der über dem Intervall $[6;9]$ in der Abbildung in b1) gezeigt wird.
Ermittle einen Funktionsterm $g^*(x)$ , und stelle diesen Term in der Form $(ax + b) \cdot \mathrm{e}^{-x+c} + 4$ mit geeigneten reellen Werten $a$ , $b$ , $c$ dar.

(4 P)

Für eine verbesserte Modellierung des Dachfirsts wird anstelle der Funktion $g$ aus Teilaufgabe b) die Verwendung der Funktionen $h_k$ und ihrer Ableitungsfunktionen $\(h$ mit

$h_k(x)=\dfrac{5}{9}(x-3)^2\cdot e^{k(x-6)}+4$

und

Gleichung anzeigen

mit $k\geq0$ vorgeschlagen.

c1)

Weise nach, dass die Funktion $g$ aus Teilaufgabe b) nicht in der Schar der Funktionen $h_k$ enthalten ist.

(2 P)

c2)

Zeige, dass der Term $5k+\dfrac{10}{3}$ die Steigung des Graphen von $h_k$ an der Stelle $x=6$ angibt.

(2 P)

c3)

So wie in der Teilaufgabe 4b) lässt sich aus dem Graphen von $h_k$ der Graph einer Funktion $h_k^*$ erzeugen. Bei $x=6$ modellieren die Graphen von $h_k$ und $h_k^*$ dann die Spitze des Dachfirsts.
Bestimme denjenigen Wert für $k$ , für den der Innenwinkel der Spitze 30° beträgt.

(4 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

Zunächst wird die allgemeine Funktionsgleichung und die ersten beiden Ableitungen einer ganzrationalen Funktion dritten Grades aufgestellt:

$\(\begin{array}[t]{rll} f(x)&=& ax^3+bx^2+cx+d &\quad \scriptsize \\[5pt] f$

Die Informationen über die Funktion $f$ ergeben folgende Gleichungen:

$f(0)= 3$
$f(3)= 4$
$\(f$
$\(f$

Aus $f(0)=3$ folgt direkt $d=3.$ Daraus folgt:

$\begin{array}[t]{rll} f(3)&=&4 &\quad \scriptsize \mid\; \\[5pt] 27a+9b+3c+3&=&4 &\quad \scriptsize \mid\; -3 \\[5pt] 27a+9b+3c&=& 1 \end{array}$

Damit muss Folgendes gelten:

Vollständigen Rechenweg anzeigen

$\(\begin{array}{lrll} \text{I}\quad&27a + 9b + 3c&=& 1 \\ \text{II$

Aus $\(\text{III$ folgt $c=1.$

Einsetzen von $c$ in $\(\text{II$ liefert:

$\begin{array}[t]{rll} 3b+2\cdot 1&=& 1 &\quad \scriptsize \mid\; -2 \\[5pt] 3b\cdot 1&=& -1 &\quad \scriptsize \mid\; :3 \\[5pt] b&=& -\dfrac{1}{3} \end{array}$

Einsetzen von $b$ und $c$ in $\text{I}$ liefert:

Vollständigen Rechenweg anzeigen

$a=\dfrac{1}{27}$

Für die Gleichung der Funktion $f$ gilt also insgesamt:

$f(x)=\dfrac{1}{27}x^3-\dfrac{1}{3}x^2+x+3$

a2)

$\begin{array}[t]{rll} f(1)&=&\dfrac{1}{27}-\dfrac{1}{3}+1+3 &\quad \scriptsize \\[5pt] &=& \dfrac{100}{27} &\quad \scriptsize \\[5pt] &\approx& 3,7 \end{array}$

Die Höhe des Dachfirsts über dem Boden an der Stelle $x=1$ beträgt etwa $37\,\text{m}$ .

a3)

$\(\begin{array}[t]{rll} f$

a4)

Wenn $\(f$ für $x\lt3$ gilt, ist der Graph von $f$ für $x$ rechtsgekrümmt. Mit $\(f$ folgt:

$\(\begin{array}[t]{rll} f$

Der Graph $f$ ist folglich für $x\lt3$ rechtsgekrümmt.

b1)

$x$	$g(x)$
$3$	$4,00$
$3,5$	$4,07$
$4$	$4,22$
$4,5$	$4,55$
$5$	$5,21$
$5,5$	$6,50$
$6$	$8,95$

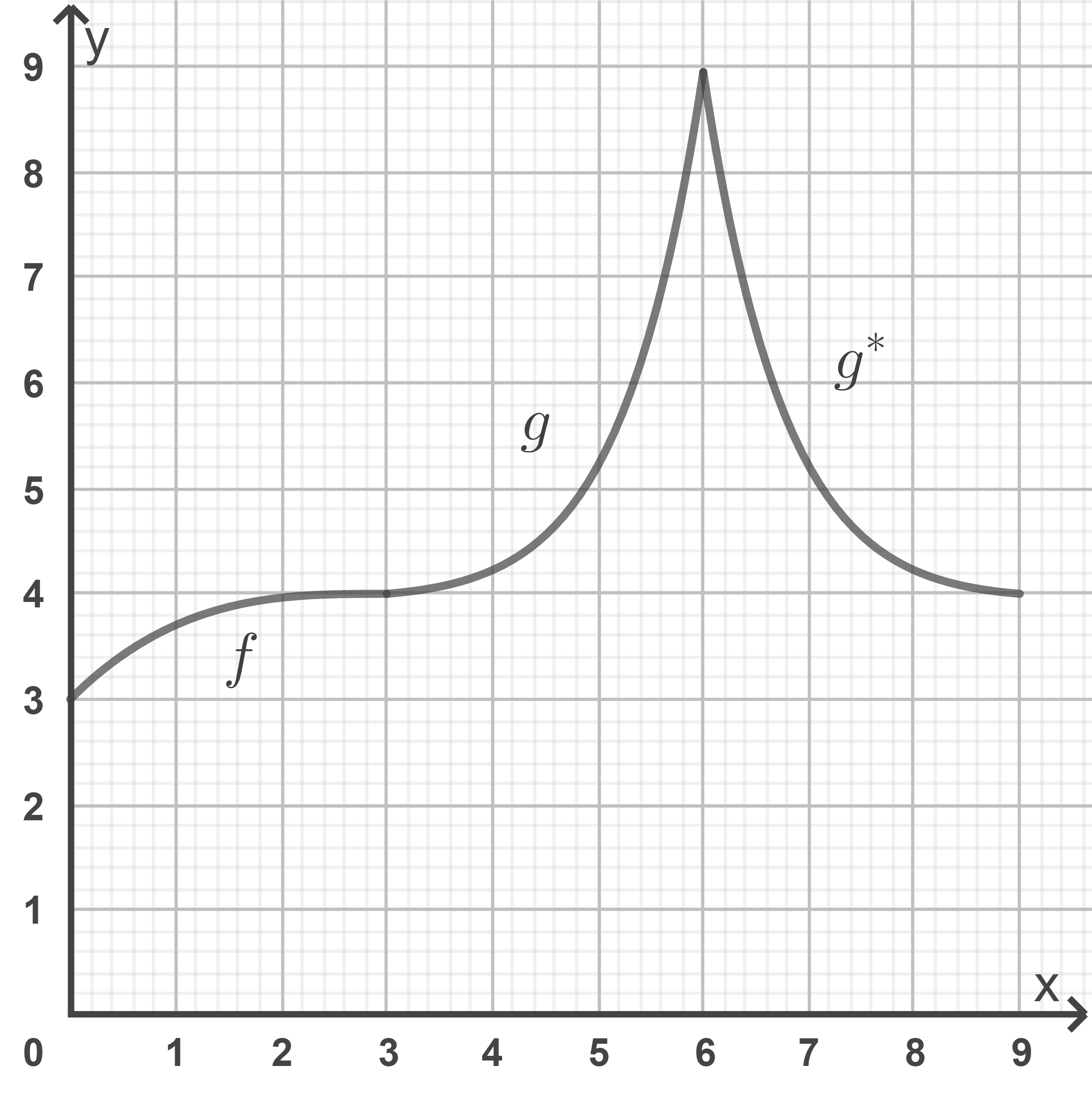
Grafik mit zwei Funktionen f und g auf einem Koordinatensystem. Die y-Achse reicht von 3 bis 9, die x-Achse von 0 bis 9.

b2)

$\(g$

$\(f$

Somit ist $\(f$ , sodass der Dachfirst an dieser Stelle durch die Graphen $f$ und $g$ nicht knickfrei modelliert werden kann.

b3)

1. Schritt: Ableitungen berechnen

$g(x)=(x-3)\cdot \mathrm e^{x-5,5}+4$

$\(g$

$\(g$ $=\mathrm e ^{x-5,5}(x-1)$

$\(g$ $=x\cdot\mathrm e ^{x-5,5}$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

3. Schritt: Hinreichende Bedingung für Extremstellen anwenden

$\(g$

Für $x=2$ ist somit die notwendige und hinreichende Bedingung einer Extremstelle erfüllt.

4. Schritt: Notwendige Bedingung für Wendestellen anwenden

$\(\begin{array}[t]{rll} g$

5. Schritt: Hinreichende Bedingung für Wendestellen anwenden

$\(g$

Für $x=1$ ist somit die notwendige und hinreichende Bedingung einer Wendestelle erfüllt.

b4)

Eine Spiegelung von $g$ an der $y$ -Achse ergibt:

$g(-x)=(-x-3)\cdot \mathrm e^{-x-5,5}+4$

Eine zusätzliche Verschiebung um 12 Einheiten nach rechts liefert:

Vollständigen Rechenweg anzeigen

$g(-(x-12)) = (-x+9)\cdot\mathrm e^{-x+6,5}+4$

Für die Funktion $g^*(x)$ ergibt sich die Funktionsgleichung $g^*(x)=(-x+9)\cdot \mathrm e^{-x+6,5}+4$ mit $a=-1$ , $b=9$ und $c=6,5$ .

c1)

Für alle $k$ gilt:

$\begin{array}[t]{rll} h_k(6)&=&\dfrac{5}{9}(6-3)^2\cdot \mathrm e^{k(6-6)}+4&\quad \scriptsize \\[5pt] &=& 5+4&\quad \scriptsize\\[5pt] &=& 9\quad \scriptsize\\[5pt] g(6)&=& (6-3)\cdot \mathrm e^{6-5,5}+4 \quad \scriptsize\\[5pt] &=& 3e^{0,5}+4 \quad \scriptsize\\[5pt] &\approx& 8,94 \end{array}$

Folglich gibt es keine Funktion $h_k$ , die an der Stelle $x=6$ mit $g$ übereinstimmt.

c2)

Rechenweg anzeigen

c3)

An der Stelle $x=6$ wird der Steigungswinkel $\alpha$ des Graphen von $h_k$ wie folgt berechnet:

$\(\tan(\alpha)= h$

Der Innenwinkel der Spitze des Dachfirsts und $2\alpha$ ergänzen sich zu $180^{\circ}$ :

$\begin{array}[t]{rll} 30^{\circ}+2\alpha&=& 180^{\circ} &\quad \scriptsize \mid -30^{\circ}\\[5pt] 2\alpha&=& 150^{\circ} &\quad \scriptsize \mid :2\\[5pt] \alpha&=& 75^{\circ} \end{array}$

Damit folgt:

$\begin{array}[t]{rll} \tan (75^{\circ})&=& 5k+\dfrac{10}{3}\\[5pt] 2+\sqrt{3}&=& 5k+\dfrac{10}{3} &\quad \scriptsize \mid -\dfrac{10}{3}\\[5pt] \dfrac{-4+3\sqrt3}{3}&=& 5k &\quad \scriptsize \mid :5\\[5pt] \dfrac{-4+3\sqrt3}{15}&=& k&\quad \scriptsize \\[5pt] 0,08 &\approx& k \end{array}$

Für $k\approx 0,08$ beträgt der Innenwinkel der Spitze $30^{\circ}$ .

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?