Analysis 2
Während eines Sommertages werden von 4:00 Uhr morgens bis 18:00 Uhr abends Wetterdaten von einer Messstation aufgenommen.
Eine Messgröße ist die Temperatur der Luft. Die Funktion  mit
mit
 und
und  beschreibt diese Messergebnisse. Dabei gibt
beschreibt diese Messergebnisse. Dabei gibt  die vergangene Zeit seit 0:00 Uhr in Stunden
die vergangene Zeit seit 0:00 Uhr in Stunden  an und
an und  die Temperatur in Grad Celsius
die Temperatur in Grad Celsius  Der Graph von
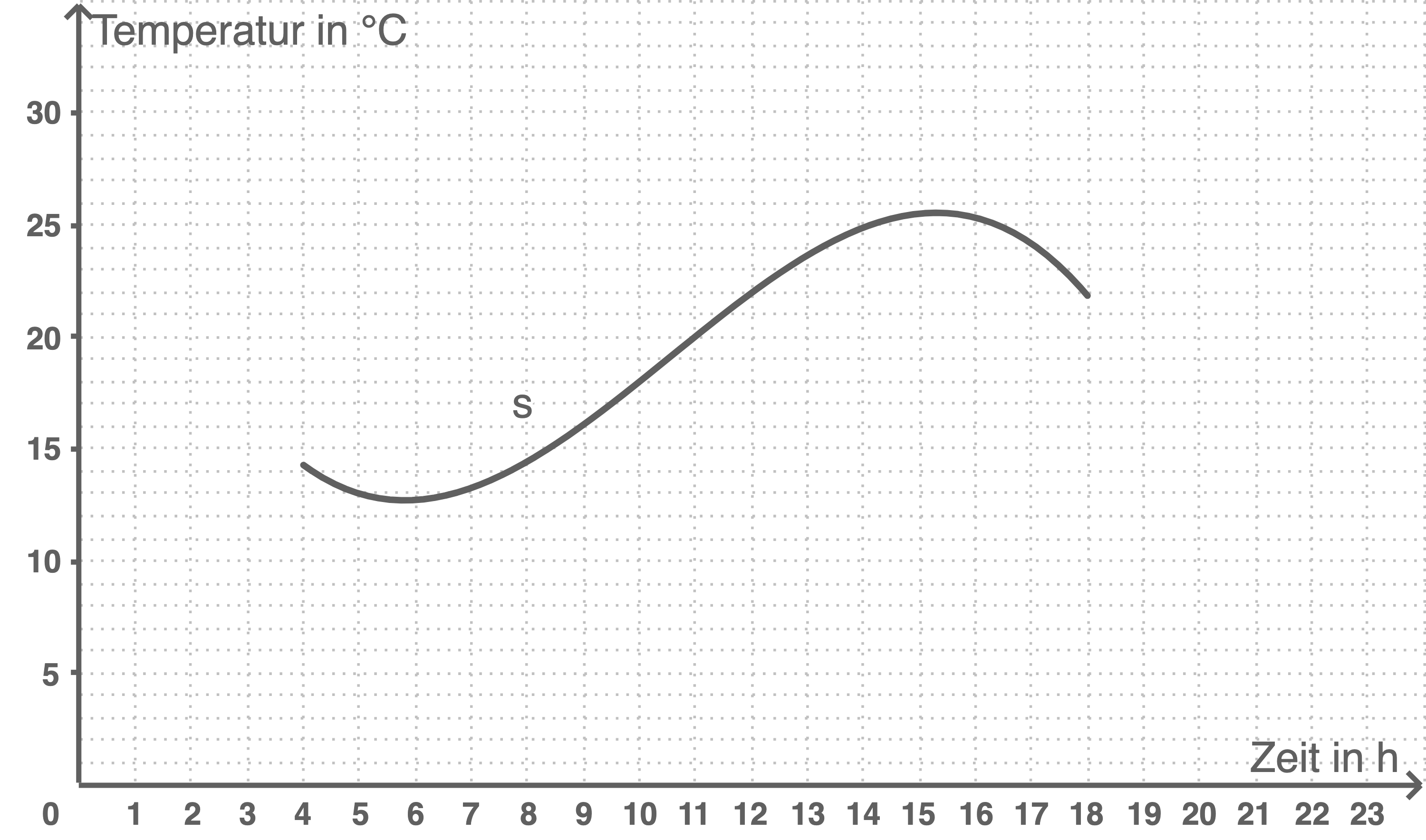
Der Graph von  ist in Abbildung 1 dargestellt.
ist in Abbildung 1 dargestellt.
 Luft enthält Wasser im gasförmigen Zustand. Die maximale Masse an Wasser, die in Luft enthalten sein kann, ist abhängig von der Temperatur.
Die Funktion
Luft enthält Wasser im gasförmigen Zustand. Die maximale Masse an Wasser, die in Luft enthalten sein kann, ist abhängig von der Temperatur.
Die Funktion  mit
mit
 beschreibt diesen Zusammenhang. Dabei ist
beschreibt diesen Zusammenhang. Dabei ist  die Temperatur in Grad Celsius.
die Temperatur in Grad Celsius.  gibt in der Einheit Gramm
gibt in der Einheit Gramm  die maximale Masse an Wasser an, die ein Kubikmeter Luft enthalten kann. Die Abbildung 2 zeigt den Graphen von
die maximale Masse an Wasser an, die ein Kubikmeter Luft enthalten kann. Die Abbildung 2 zeigt den Graphen von 
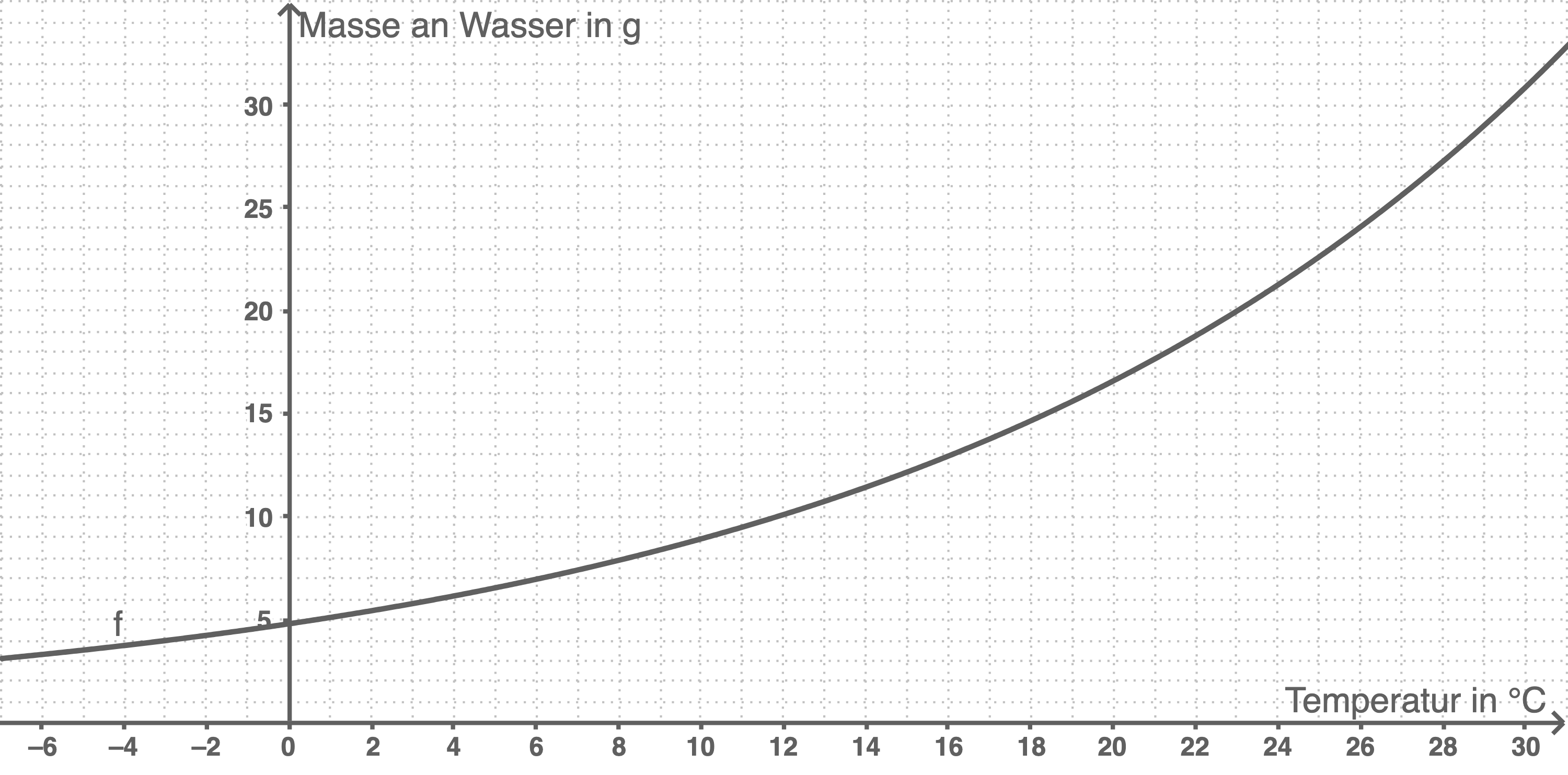

Abbildung 1
a)
a1)
Bestimme rechnerisch die maximale und die minimale Temperatur im Messzeitraum.
(5 BE)
a2)
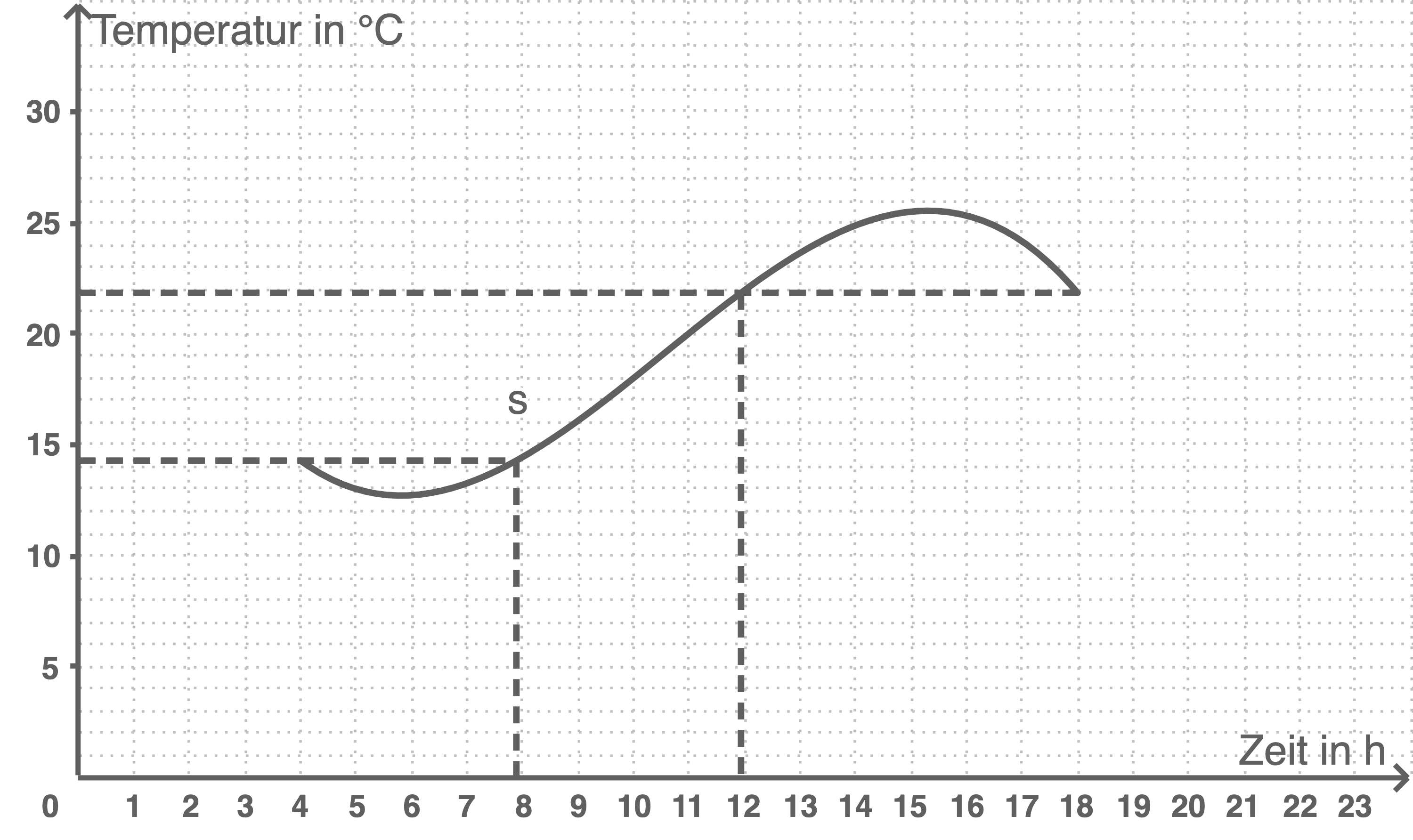
Außer der maximalen und der minimalen Temperatur gibt es weitere Temperaturen, die bei dieser Messung nur einmal auftreten.
Ermittle näherungsweise anhand der Abbildung 1 diese Temperaturen und die entsprechenden Uhrzeiten. Zeichne dazu geeignete Hilfslinien ein.
(4 BE)
a3)
Berechne sowohl die größte als auch die kleinste momentane Änderungsrate der Temperatur im Messzeitraum.
(5 BE)
a4)
Berechne den Wert des Terms  und gib die Bedeutung dieses Terms im Sachzusammenhang an.
und gib die Bedeutung dieses Terms im Sachzusammenhang an.
(3 BE)

Abbildung 2
b)
b1)
Berechne  sowie die Stelle
sowie die Stelle  mit
mit 
(2 BE)
b2)
Beurteile die folgende Aussage:
Es gibt eine Stelle  an der der Funktionswert von
an der der Funktionswert von  und die Steigung des Graphen von
und die Steigung des Graphen von  gleich groß sind.
gleich groß sind.
(5 BE)
b3)
Die Funktion  wächst streng monoton. Interpretiere diese Tatsache im Sachzusammenhang.
wächst streng monoton. Interpretiere diese Tatsache im Sachzusammenhang.
(2 BE)
c)
Die Messstation ermittelt auch die sogenannte relative Luftfeuchtigkeit, die als Prozentsatz  angegeben wird. Die relative Luftfeuchtigkeit ist der Anteil der Masse an Wasser in der Luft bezogen auf die maximale Masse an Wasser, die in Luft enthalten sein kann.
angegeben wird. Die relative Luftfeuchtigkeit ist der Anteil der Masse an Wasser in der Luft bezogen auf die maximale Masse an Wasser, die in Luft enthalten sein kann.
c1)
Für jeden Wert  mit
mit  beschreibt die Funktion
beschreibt die Funktion  mit
mit  den Zusammenhang zwischen der Temperatur und der Masse an Wasser in der Luft bei einer vorliegenden relativen Luftfeuchtigkeit von
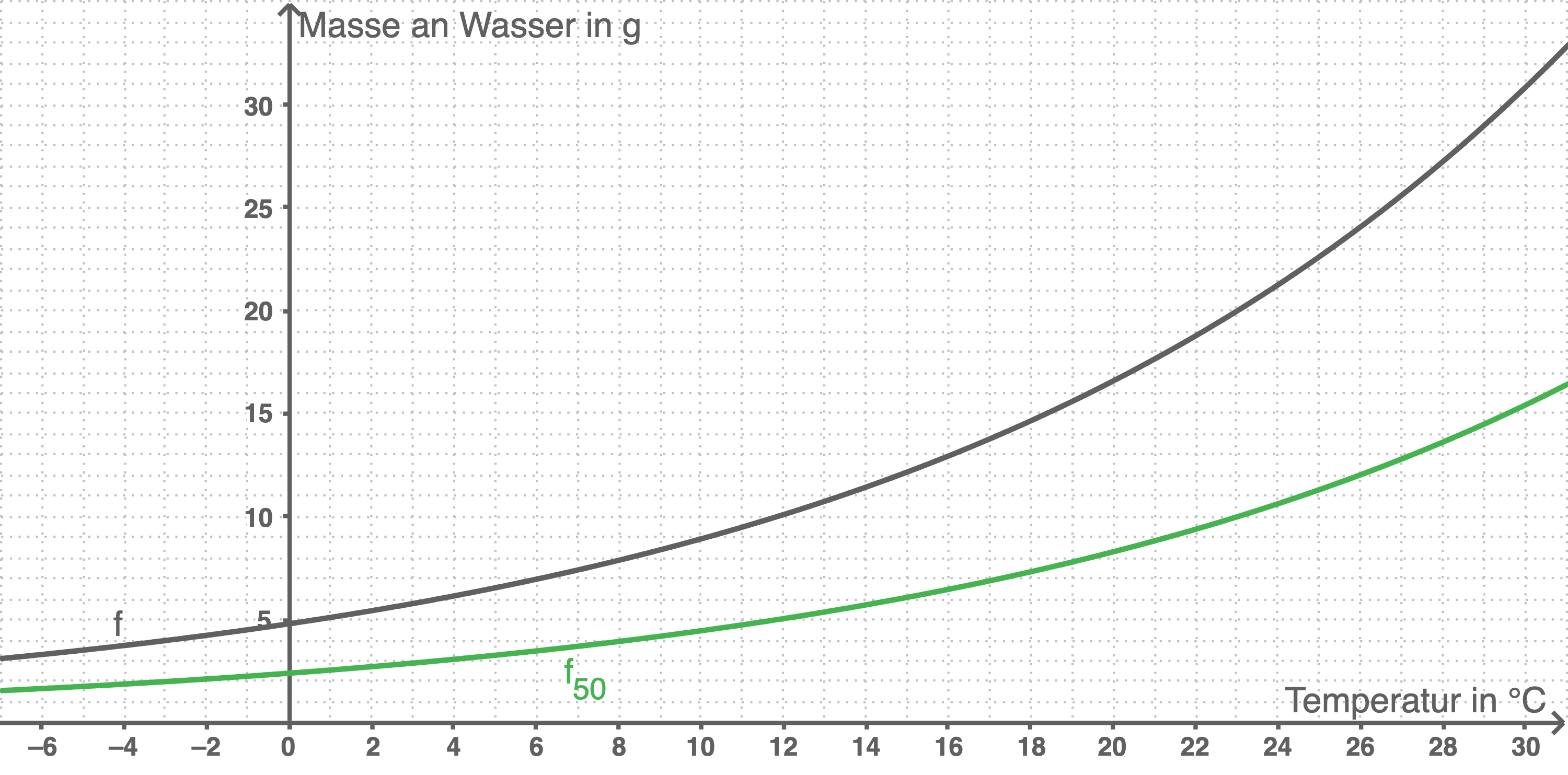
den Zusammenhang zwischen der Temperatur und der Masse an Wasser in der Luft bei einer vorliegenden relativen Luftfeuchtigkeit von  Zeichne den Graphen der Funktion
Zeichne den Graphen der Funktion  in die Abbildung 2.
in die Abbildung 2.
(3 BE)
c2)
Am Tag der Messung liegt um 15 Uhr eine relative Luftfeuchtigkeit von  vor.
Bestimme, welche relative Luftfeuchtigkeit um 18 Uhr vorliegt, falls die Masse an Wasser in der Luft unverändert bleibt.
vor.
Bestimme, welche relative Luftfeuchtigkeit um 18 Uhr vorliegt, falls die Masse an Wasser in der Luft unverändert bleibt.
(5 BE)
d)
Die Messwerte der Temperatur der Luft im Verlauf des nächsten Tages werden mit Hilfe einer ganzrationalen Funktion  dritten Grades in Abhängigkeit von
dritten Grades in Abhängigkeit von  beschrieben. Dabei gibt
beschrieben. Dabei gibt  wieder die Zeit in Stunden seit 0:00 Uhr an und
wieder die Zeit in Stunden seit 0:00 Uhr an und  die Temperatur in Grad Celsius.
Bei der Auswertung der Wetterdaten wird die Verkettung
die Temperatur in Grad Celsius.
Bei der Auswertung der Wetterdaten wird die Verkettung  der Funktionen
der Funktionen  und
und  mit dem Funktionsterm
mit dem Funktionsterm  betrachtet.
betrachtet.
d1)
Gib die Bedeutung des Werts  im Sachzusammenhang an.
im Sachzusammenhang an.
(2 BE)
d2)
Im Folgenden werden die Funktionen  und
und  auf ganz
auf ganz  betrachtet. Für den Term
betrachtet. Für den Term  der ersten Ableitungsfunktion von
der ersten Ableitungsfunktion von  gilt die Gleichung
gilt die Gleichung
 Weiterhin gilt
Weiterhin gilt  für alle
für alle  Begründe damit die folgende Aussage:
Wenn
Begründe damit die folgende Aussage:
Wenn  eine lokale Maximalstelle von
eine lokale Maximalstelle von  ist, dann ist
ist, dann ist  auch eine lokale Maximalstelle von
auch eine lokale Maximalstelle von 
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a1)
a2)
a3)
a4)
Der Term beschreibt den Mittelwert der von 4 Uhr bis 18 Uhr gemessenen Temperaturen in 
b1)
Zuerst wird der Wert der Funktion  an der Stelle
an der Stelle  berechnet:
berechnet:
![\(\begin{array}[t]{rll}
f(10) &=& 4,8 \cdot \mathrm e^{0,062 \cdot 10} \\
&=& 4,8 \cdot \mathrm e^{0,62} \\
&\approx& 8,92
\end{array}\)](https://mathjax.schullv.de/2731cab6e356a45cfc457882cb0b18a24317298f48b528543888082f257999ec?color=5a5a5a) Nun wird die Stelle
Nun wird die Stelle  bestimmt, an der
bestimmt, an der  gilt:
gilt:
![\(\begin{array}[t]{rll}
4,8 \cdot \mathrm e^{0,062 \cdot x} &=& 20 &\quad \scriptsize \mid\; :4,8 \\
\mathrm e^{0,062 \cdot x} &=& \dfrac{20}{4,8} &\quad \scriptsize \mid\; \ln \\
0,062x &=& \ln\left(\dfrac{20}{4,8}\right) &\quad \scriptsize \mid \;:0,062 \\
x &\approx& 23,02
\end{array}\)](https://mathjax.schullv.de/c01d1432870491b0a3758bf2e9cd02883779103f46aff854c8b279fedd9fce9d?color=5a5a5a) Somit ist
Somit ist  und die Stelle, bei der
und die Stelle, bei der  ist, liegt bei
ist, liegt bei  .
.
b2)
An einer solchen Stelle  würde
würde  gelten. Für die Ableitung von
gelten. Für die Ableitung von  gilt:
gilt:
 Da stets
Da stets  gilt, folgt:
Da dies ein Widerspruch ist, gibt es keine solche Stelle
gilt, folgt:
Da dies ein Widerspruch ist, gibt es keine solche Stelle  die Aussage ist also falsch.
die Aussage ist also falsch.
b3)
Je höher die Temperatur ist, desto mehr Wasser kann die Luft maximal enthalten.
c1)
c2)
Wegen  beträgt die Temperatur um 15 Uhr
beträgt die Temperatur um 15 Uhr  Da
Da  ist, liegen ca.
ist, liegen ca.  Wasser in einem Kubikmeter Luft vor.
Wegen
Wasser in einem Kubikmeter Luft vor.
Wegen  beträgt die Temperatur um 18 Uhr noch
beträgt die Temperatur um 18 Uhr noch  Der Anteil
Der Anteil  entspricht somit einer relativen Luftfeuchtigkeit von ca.
entspricht somit einer relativen Luftfeuchtigkeit von ca.  .
.
d1)
Der Wert beschreibt die maximale Masse an Wasser in Gramm, die ein Kubikmeter Luft um 12 Uhr am nächsten Tag enthalten kann.
d2)
Wenn  eine lokale Maximalstelle von
eine lokale Maximalstelle von  ist, wechselt
ist, wechselt  an der Stelle
an der Stelle  das Vorzeichen von positiv zu negativ. Da laut Aufgabenstellung für alle
das Vorzeichen von positiv zu negativ. Da laut Aufgabenstellung für alle  gilt, dass
gilt, dass  hat
hat  stets dasselbe Vorzeichen wie
stets dasselbe Vorzeichen wie  Somit vollzieht auch
Somit vollzieht auch  an der Stelle
an der Stelle  einen Vorzeichenwechsel von positiv zu negativ.
einen Vorzeichenwechsel von positiv zu negativ.