Analysis 2
Mit ferngesteuerten Fahrzeugen, sogenannten Buggys, werden Rennen auf speziellen Fahrbahnen gefahren. Ein erster Fahrbahnabschnitt vom Startpunkt  zum Punkt
zum Punkt  wird mithilfe einer Funktion
wird mithilfe einer Funktion  modelliert. An der Stelle
modelliert. An der Stelle  gibt
gibt  die Höhe der Fahrbahn an. Auf beiden Achsen im zugehörigen Koordinatensystem entspricht eine Längeneinheit einem Meter in der Wirklichkeit.
die Höhe der Fahrbahn an. Auf beiden Achsen im zugehörigen Koordinatensystem entspricht eine Längeneinheit einem Meter in der Wirklichkeit.
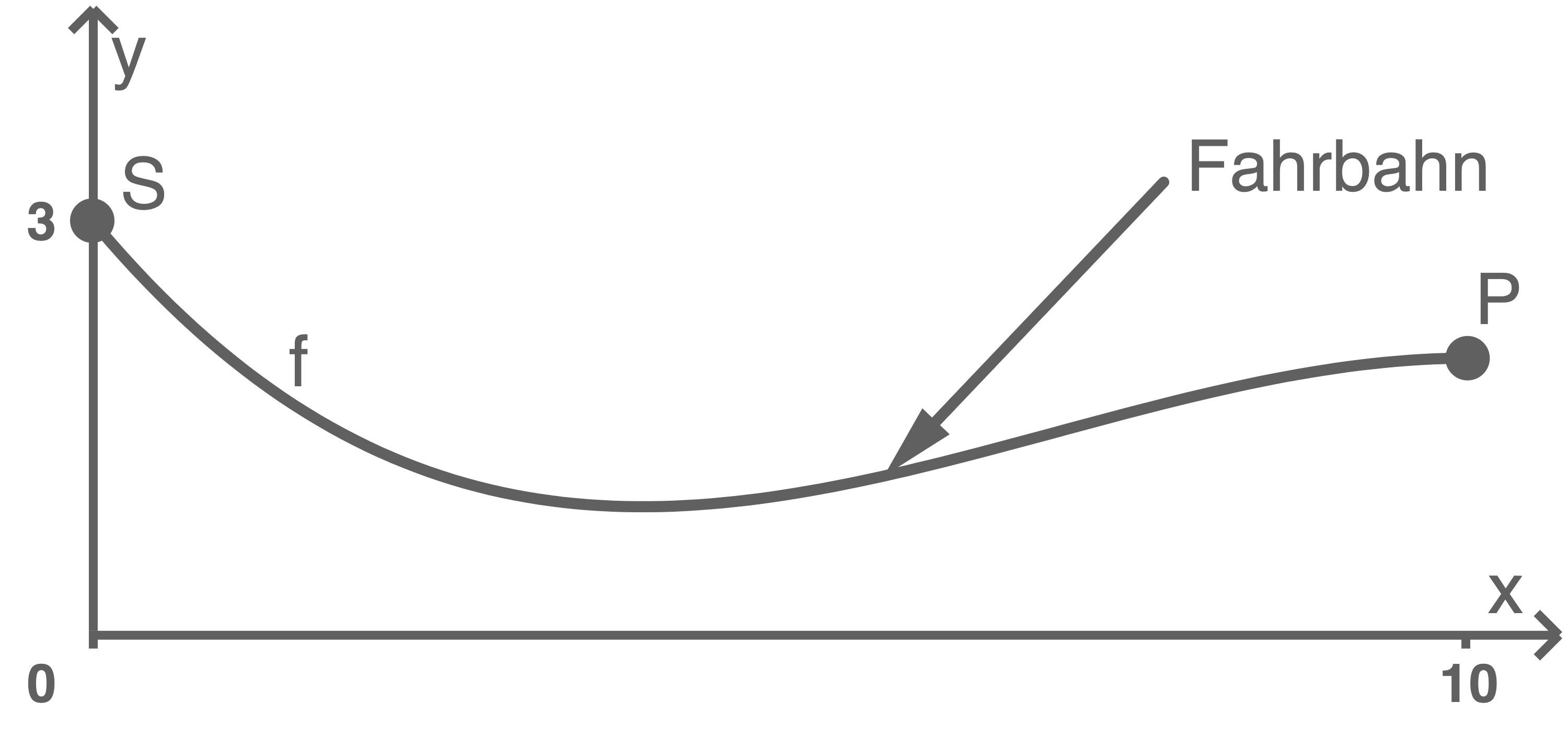
 mit
mit ![\(x \in[0 ; 10] .\)](https://mathjax.schullv.de/f41ff429720fb6143c939c46ff20c423621c2834a4124dc86d60e8911bf63fb9?color=5a5a5a) Ein Buggy fährt von
Ein Buggy fährt von  nach
nach  . Während der Fahrt nimmt die Höhe der Fahrbahn zunächst ab, bis sie ihren Minimalwert erreicht, und nimmt anschließend wieder zu.
Ein zweiter Fahrbahnabschnitt wird durch die Funktion
. Während der Fahrt nimmt die Höhe der Fahrbahn zunächst ab, bis sie ihren Minimalwert erreicht, und nimmt anschließend wieder zu.
Ein zweiter Fahrbahnabschnitt wird durch die Funktion  mit
mit
 und
und ![\( x \in[10 ; 14]\)](https://mathjax.schullv.de/fce1d9f2a6e8fc4bc618940577655d7da2a02b54de01ebf53b5439c2d02454ae?color=5a5a5a) modelliert. An der Stelle
modelliert. An der Stelle  gibt
gibt  die Höhe der Fahrbahn an.
die Höhe der Fahrbahn an.
 Wertetabelle zu Teilaufgabe c1)
Wertetabelle zu Teilaufgabe c1)

a)
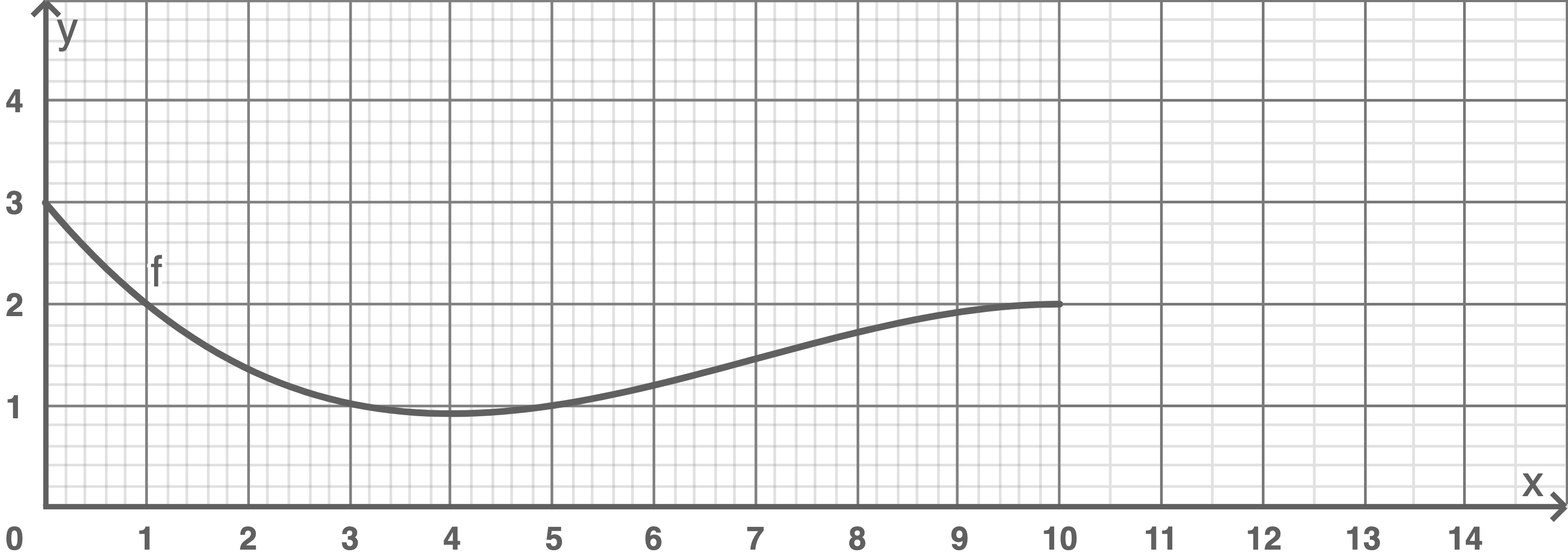
Auf dem Beiblatt ist der Graph der Funktion  größer dargestellt.
größer dargestellt.
Verwende für den ersten Fahrbahnabschnitt im Folgenden
a1)
Gib mithilfe des Graphen die Höhe der Fahrbahn an der Stelle  an.
an.
(1 P)
a2)
Bestimme unter Verwendung geeigneter Hilfslinien in der Abbildung auf dem Beiblatt
- die Stellen, an denen die Fahrbahnhöhe
beträgt, und
- die Steigung der Fahrbahn an der Stelle
(5 P)
b)
b1)
Berechne die minimale Höhe der Fahrbahn.
(4 P)
b2)
Berechne die maximale Steigung, die der Buggy während der Fahrt überwindet.
(5 P)
b3)
Die Länge  des Graphen der Funktion
des Graphen der Funktion  über dem Intervall
über dem Intervall ![\([a ; b]\)](https://mathjax.schullv.de/9082d98d4e7f9402e9c1d5c1e0b40655337b007d919508a2ded32428ee030fc3?color=5a5a5a) kann durch
kann durch  berechnet werden.
Berechne die Länge des Fahrbahnabschnitts.
berechnet werden.
Berechne die Länge des Fahrbahnabschnitts.
(3 P)
c)
c1)
Zeichne in die Abbildung auf dem Beiblatt den Graphen der Funktion  unter Verwendung der dort angegebenen Wertetabelle.
unter Verwendung der dort angegebenen Wertetabelle.
(2 P)
c2)
Bestimme einen Term der ersten Ableitungsfunktion  von
von 
(2 P)
c3)
Der Graph von  schließt im Punkt
schließt im Punkt  an den Graphen von
an den Graphen von  an. Untersuche, ob dieser Anschluss knickfrei ist.
an. Untersuche, ob dieser Anschluss knickfrei ist.
(2 P)
c4)
Für jedes  ist die Funktion
ist die Funktion  mit
mit  und
und ![\(x \in[10 ; 14]\)](https://mathjax.schullv.de/04cd44dee966348f9a51838f5a50a98fd904728f2fb9b0a492a6c774a0be7d03?color=5a5a5a) gegeben.
gegeben.
- Weise nach, dass alle Funktionsgraphen der Schar durch den Punkt
verlaufen.
- Zeige, dass
der einzige Punkt ist, den je zwei verschiedene Graphen der Schar gemeinsam haben.
(5 P)
d)
Ein Buggy fährt mit so hoher Geschwindigkeit, dass er am Übergang der beiden Fahrbahnabschnitte an der Stelle  den Kontakt zur Fahrbahn verliert und ein Stück fliegt, bis er auf der durch
den Kontakt zur Fahrbahn verliert und ein Stück fliegt, bis er auf der durch  modellierten Fahrbahn landet und weiterfährt.
Die Flugbahn lässt sich mithilfe einer Parabel beschreiben. Diese besitzt den Scheitelpunkt
modellierten Fahrbahn landet und weiterfährt.
Die Flugbahn lässt sich mithilfe einer Parabel beschreiben. Diese besitzt den Scheitelpunkt  und schneidet den Graphen von
und schneidet den Graphen von  an der Stelle
an der Stelle 
Material (Beiblatt)
d1)
Leite einen Funktionsterm der Funktion  her, deren Graph diese Parabel ist.
[Kontrolle:
her, deren Graph diese Parabel ist.
[Kontrolle:  ]
]
(4 P)
d2)
Berechne die durchschnittliche Höhe der Flugbahn über der Fahrbahn.
(3 P)
d3)
Im Allgemeinen hängen die Weite des Fluges und die Geschwindigkeit  des Buggys an der Stelle
des Buggys an der Stelle  an der dieser den Kontakt zur Fahrbahn verliert, voneinander ab.
Die zugehörige Flugbahn wird für
an der dieser den Kontakt zur Fahrbahn verliert, voneinander ab.
Die zugehörige Flugbahn wird für  beschrieben mithilfe einer Parabel mit dem Funktionsterm
beschrieben mithilfe einer Parabel mit dem Funktionsterm
 Diese Parabel schneidet den Graphen von
Diese Parabel schneidet den Graphen von  an der Stelle
an der Stelle  mit
mit  Zeige, dass
Zeige, dass  gilt.
gilt.
(4 P)

Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a1)
Aus der Abbildung auf dem Beiblatt lässt sich  ablesen.
ablesen.
An der Stelle ist die Fahrbahn also
ist die Fahrbahn also  hoch.
hoch.
An der Stelle
a2)
Stellen mit einer Fahrbahnhöhe von 1,6 m bestimmen
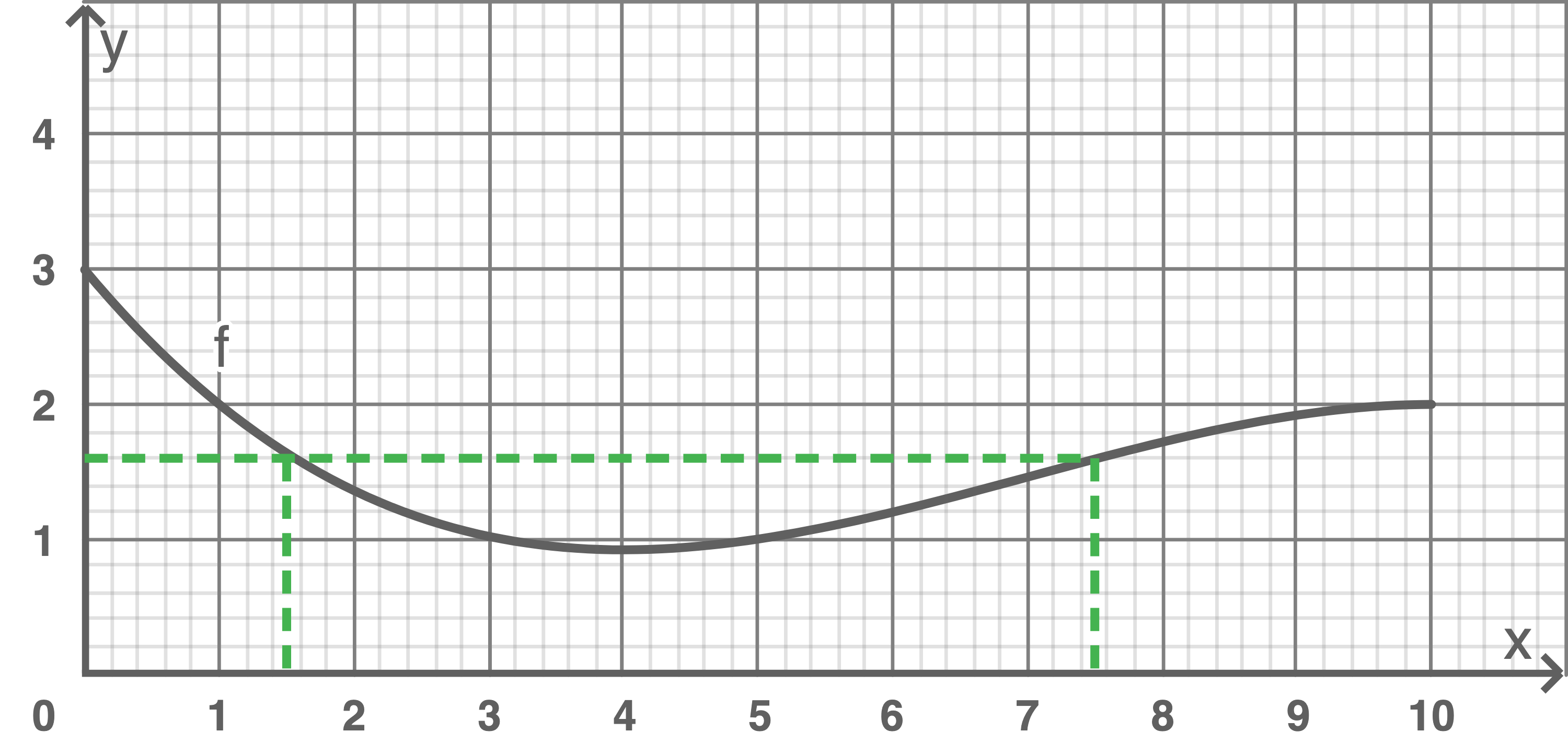 Steigung bestimmen
Die Steigung der Fahrbahn an der Stelle
Steigung bestimmen
Die Steigung der Fahrbahn an der Stelle  kann mit Hilfe der Tangente
kann mit Hilfe der Tangente  an den Graphen von
an den Graphen von  an der Stelle
an der Stelle  bestimmt werden.
bestimmt werden.
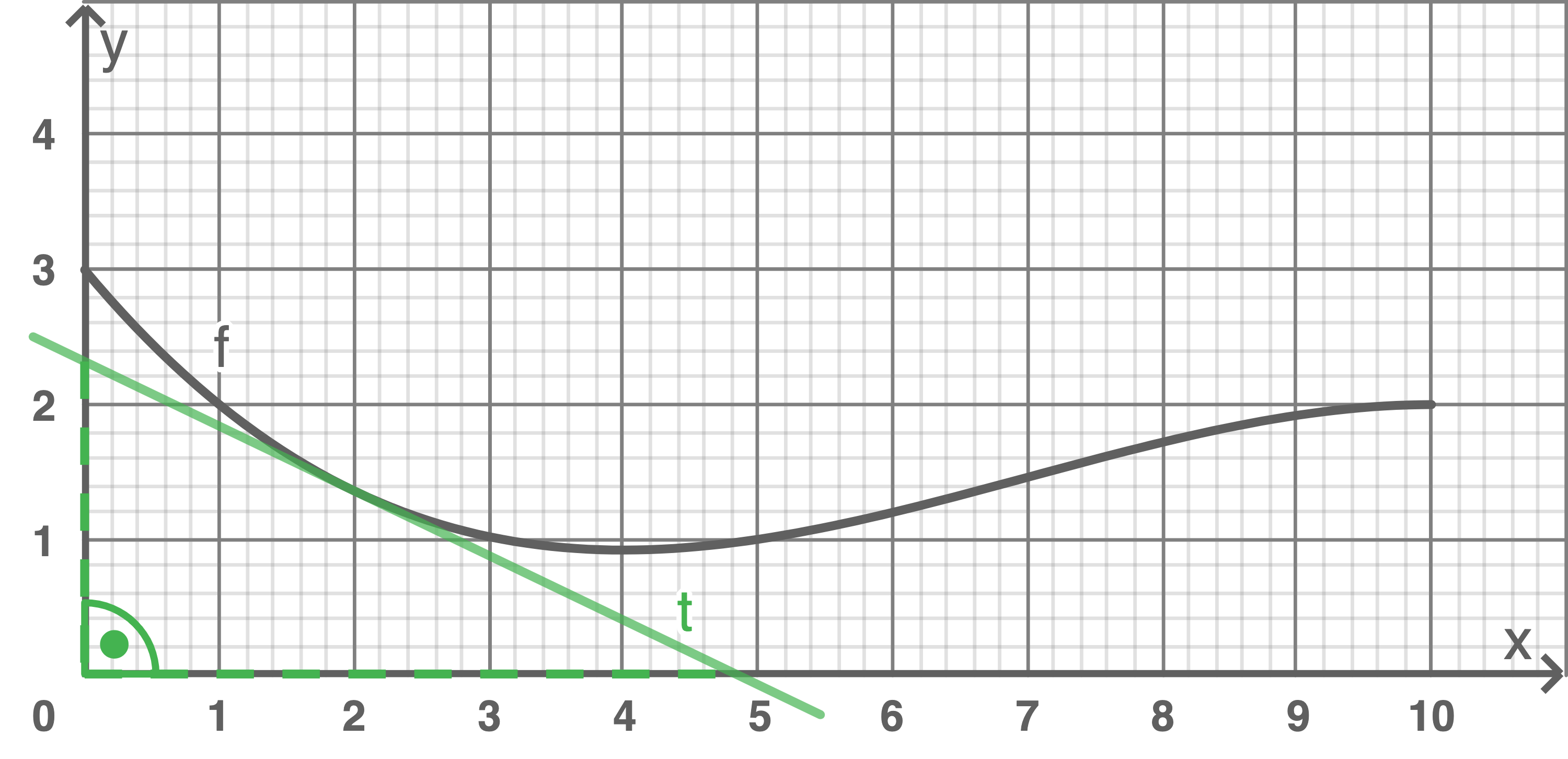 An die Tangente lässt sich ein Steigungsdreieck anlegen. Die Tangente verläuft in etwa durch die Punkte
An die Tangente lässt sich ein Steigungsdreieck anlegen. Die Tangente verläuft in etwa durch die Punkte  und
und  Für die Steigung an der Stelle
Für die Steigung an der Stelle  ergibt sich daher:
ergibt sich daher:



b1)
Laut Aufgabenstellung nimmt die Höhe der Fahrbahn zunächst ab, bis sie ihren Minimalwert erreicht und nimmt dann wieder zu. Daher wird die minimale Höhe im Tiefpunkt des Graphen von  angenommen.
1. Schritt: Notwendiges Kriterium für Extrempunkte anwenden
Für eine Extremstelle
angenommen.
1. Schritt: Notwendiges Kriterium für Extrempunkte anwenden
Für eine Extremstelle  von
von  muss
muss  erfüllt sein. Für die erste Ableitung gilt:
erfüllt sein. Für die erste Ableitung gilt:
 Gleichsetzen:
Gleichsetzen:
 liegt bereits am Ende des betrachteten Fahrbahnabschnitts und kann wegen der Beschreibung in der Aufgabenstellung daher nicht die Stelle mit der minimalen Höhe sein.
2. Schritt: Höhe berechnen
liegt bereits am Ende des betrachteten Fahrbahnabschnitts und kann wegen der Beschreibung in der Aufgabenstellung daher nicht die Stelle mit der minimalen Höhe sein.
2. Schritt: Höhe berechnen

 Die minimale Höhe der Fahrbahn beträgt
Die minimale Höhe der Fahrbahn beträgt 
b2)
Die maximale Steigung entspricht dem globalen Maximum von  1. Schritt: Notwendiges Kriterium für Extremstellen von
1. Schritt: Notwendiges Kriterium für Extremstellen von  anwenden
Für ein lokales Maximum von
anwenden
Für ein lokales Maximum von  an der Stelle
an der Stelle  im Inneren des Definitionsbereichs muss wegen des notwendigen Kriteriums für Extremstellen
im Inneren des Definitionsbereichs muss wegen des notwendigen Kriteriums für Extremstellen  gelten.
gelten.
 Gleichsetzen:
Gleichsetzen:
![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/aae35677edcdf4d56727c7bda4e7f51ebbfbb5d9d17df7af757ac8660b516f3f?color=5a5a5a) 2. Schritt: Auf Randextrema überprüfen
2. Schritt: Auf Randextrema überprüfen


 Mit dem Vorzeichenwechselkriterium ist eine hinreichende Bedingung für ein lokales Maximum der 1 . Ableitung von
Mit dem Vorzeichenwechselkriterium ist eine hinreichende Bedingung für ein lokales Maximum der 1 . Ableitung von  an der Stelle
an der Stelle  erfüllt.
erfüllt.
Zugleich zeigen die Werte von an den Rändern, dass dieses auch das globale Maximum ist.
Die maximale Steigung beträgt
an den Rändern, dass dieses auch das globale Maximum ist.
Die maximale Steigung beträgt 
Zugleich zeigen die Werte von
b3)
Die Fahrbahn hat eine Länge von ca. 
c1)
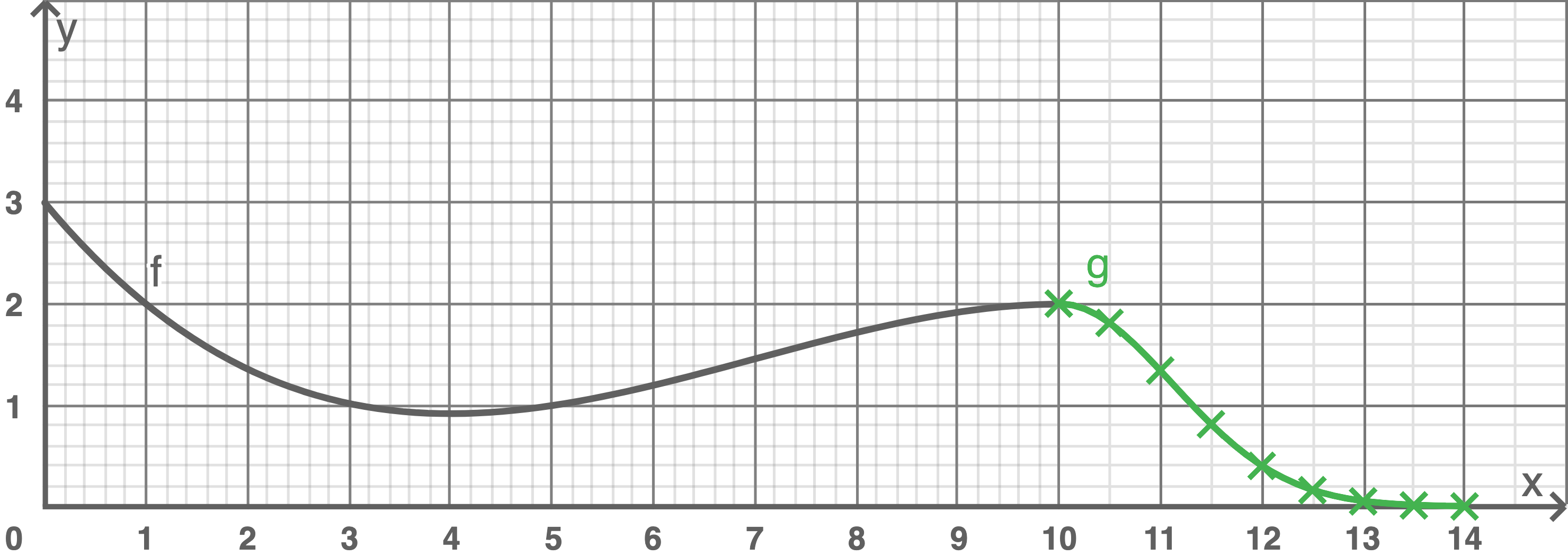
c2)
Mit der Kettenregel folgt:



c3)
Für einen knickfreien Anschluss, müssen die Graphen von  und
und  an der Übergangsstelle
an der Übergangsstelle  die gleiche Steigung haben. Es muss also
die gleiche Steigung haben. Es muss also  überprüft werden:
überprüft werden:
 (siehe b2) )
(siehe b2) )
 Da
Da  gilt, ist der Anschluss knickfrei.
gilt, ist der Anschluss knickfrei.
c4)
Verlauf der Graphen durch den Punkt nachweisen
 Für alle
Für alle  gilt
gilt  Somit verlaufen alle Graphen der Schar durch den Punkt
Somit verlaufen alle Graphen der Schar durch den Punkt  Einzigen gemeinsamen Punkt zeigen
Betrachtet werden
Einzigen gemeinsamen Punkt zeigen
Betrachtet werden  mit
mit  und
und  sowie
sowie  Für einen gemeinsamen Punkt
Für einen gemeinsamen Punkt  muss
muss  erfüllt sein:
Da es also keine weiteren Schnittstellen gibt, ist
erfüllt sein:
Da es also keine weiteren Schnittstellen gibt, ist  der einzige Punkt, den je zwei verschiedene Graphen der Schar gemeinsam haben.
der einzige Punkt, den je zwei verschiedene Graphen der Schar gemeinsam haben.
d1)
Mit der Scheitelpunktform gilt:
 wobei
wobei  die Koordinaten des Scheitelpunkts sind.
Mit dem Scheitelpunkt
die Koordinaten des Scheitelpunkts sind.
Mit dem Scheitelpunkt  folgt also:
folgt also:
 Die Parabel soll zudem den Graphen von
Die Parabel soll zudem den Graphen von  an der Stelle
an der Stelle  schneiden. Also gilt:
schneiden. Also gilt:

 Einsetzen in die Funktionsgleichung von
Einsetzen in die Funktionsgleichung von  Damit folgt:
Damit folgt:

d2)
Die Höhe der Flugbahn über der Fahrbahn wird für ![\(x\in [10;12,3]\)](https://mathjax.schullv.de/985506603a23ad7581e4fb1b99d4ccef9e1b9f64d5aef1210786f26ef7907e50?color=5a5a5a) durch die Differenzenfunktion
durch die Differenzenfunktion  beschrieben:
beschrieben:

 Gesucht ist also der durchschnittliche Funktionswert von
Gesucht ist also der durchschnittliche Funktionswert von  im Intervall
im Intervall ![\([10;12,3].\)](https://mathjax.schullv.de/5151576aa6987163115bf7c871226c399b22cbbee31e147e1272856410c0bf5b?color=5a5a5a) Diesder kann mit der zugehörigen Formel und dem Taschenrechner berechnet werden:
Die durchschnittliche Flughöhe über der Fahrbahn beträgt ca.
Diesder kann mit der zugehörigen Formel und dem Taschenrechner berechnet werden:
Die durchschnittliche Flughöhe über der Fahrbahn beträgt ca. 
d3)
An der Stelle  schneiden sich die Graphen von
schneiden sich die Graphen von  und
und  Also gilt:
Da Geschwindigkeiten nicht negativ sein können, folgt
Also gilt:
Da Geschwindigkeiten nicht negativ sein können, folgt 