Stochastik
Alle in deinen Lösungen verwendeten Zufallsgrößen müssen explizit eingeführt werden.
Mache auch Angaben über die Verteilung der jeweiligen Zufallsgrößen. Ein Fahrradhändler hat festgestellt, dass es sich bei aller von ihm verkauften Fahrräder um Mountainbikes handelt. Es soll davon ausgegangen werden, dass in einer zufälligen Auswahl verkaufter Fahhräder die Anzahl der Mountainbikes binomialverteilt ist.
aller von ihm verkauften Fahrräder um Mountainbikes handelt. Es soll davon ausgegangen werden, dass in einer zufälligen Auswahl verkaufter Fahhräder die Anzahl der Mountainbikes binomialverteilt ist.
Mache auch Angaben über die Verteilung der jeweiligen Zufallsgrößen. Ein Fahrradhändler hat festgestellt, dass es sich bei
a)
a1)
Bestimme die Wahrscheinlichkeit dafür, dass sich in einer zufälligen Auswahl von  verkauften Fahrrädern
verkauften Fahrrädern
- genau
Mountainbikes befinden;
- mindestens
und weniger als
Mountainbikes befinden.
(5 P)
a2)
Ermittle die Wahrscheinlichkeit dafür, dass in einer zufälligen Auswahl von  verkauften Fahrrädern die Anzahl der Mountainbikes um mindestens
verkauften Fahrrädern die Anzahl der Mountainbikes um mindestens  größer ist als der Erwartungswert für diese Anzahl.
größer ist als der Erwartungswert für diese Anzahl.
(3 P)
a3)
Beschreibe im Sachzusammenhang ein Zufallsexperiment, bei dem die Wahrscheinlichkeit eines Ereignisses mit dem Term
 berechnet werden kann. Gib dieses Ereignis an.
berechnet werden kann. Gib dieses Ereignis an.
(3 P)
a4)
Der Händler hat berechnet, dass er im September des Jahres 2020 mit einer Wahrscheinlichkeit von mehr als  mehr als
mehr als  Mountainbikes verkaufen wird.
Mountainbikes verkaufen wird.
Ermittle, von welcher Anzahl verkaufter Fahrräder er bei seiner Berechnung mindestens ausgegangen ist.
Ermittle, von welcher Anzahl verkaufter Fahrräder er bei seiner Berechnung mindestens ausgegangen ist.
(4 P)
b)
Der Anteil der Mountainbikes unter allen verkauften Fahrrädern beträgt weiterhin 
 aller verkauften Fahrräder haben einen Rahmen aus Aluminium.
aller verkauften Fahrräder haben einen Rahmen aus Aluminium.  aller verkauften Fahrräder sind weder Mountainbikes noch haben sie einen Rahmen aus Aluminium.
aller verkauften Fahrräder sind weder Mountainbikes noch haben sie einen Rahmen aus Aluminium.
Bestimme den Anteil der Fahrräder mit einem Rahmen aus Aluminium unter den verkauften Mountainbikes.
Bestimme den Anteil der Fahrräder mit einem Rahmen aus Aluminium unter den verkauften Mountainbikes.
(4 P)
c)
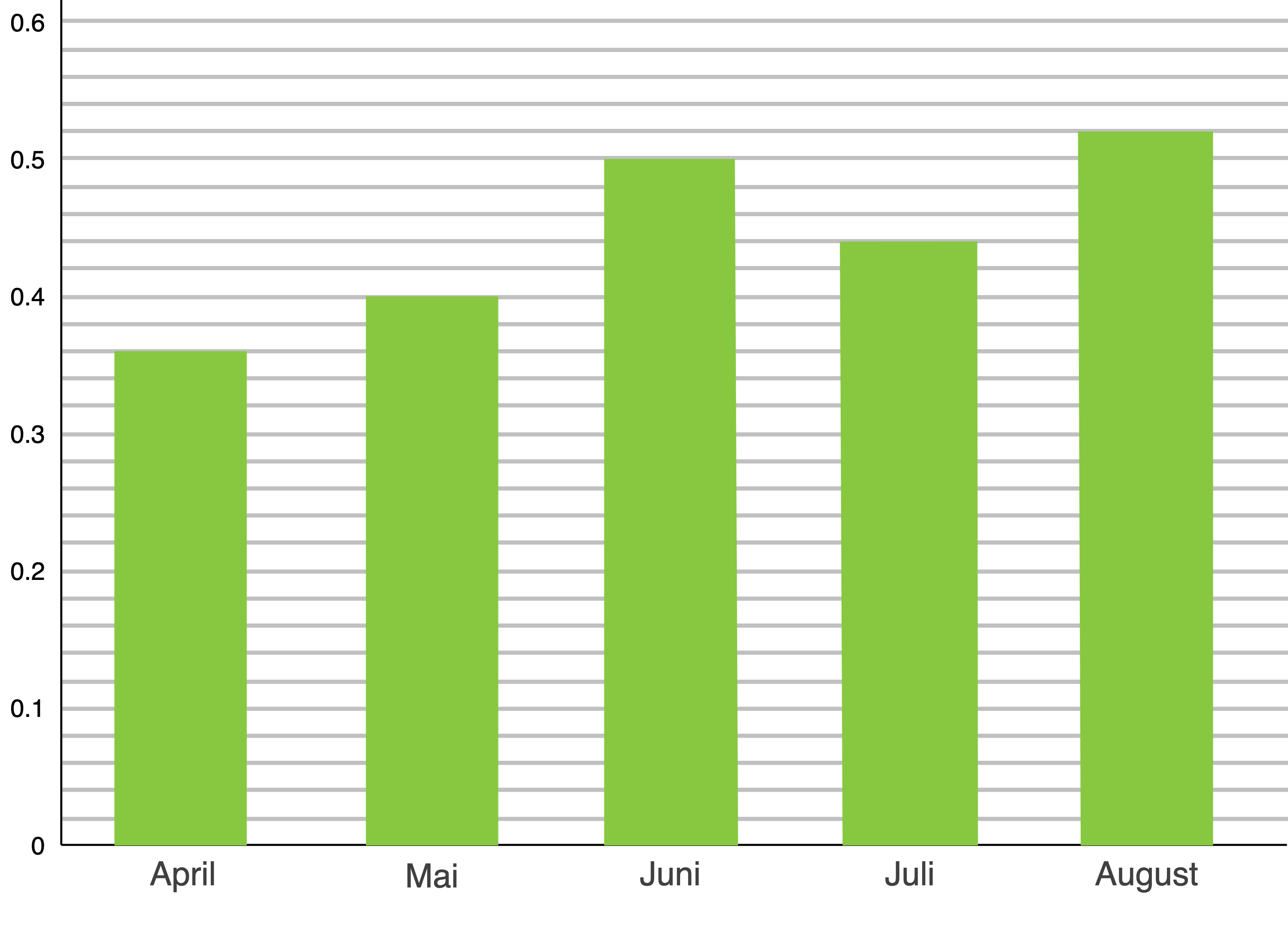
Die Abbildung zeigt für einige Monate des Jahres 2019 jeweils den Anteil der Mountainbikes unter allen verkauften Fahrrädern.

c1)
Im April wurden  Mountainbikes verkauft. Bestimme für diesen Monat die Anzahl aller verkauften Fahrräder.
Mountainbikes verkauft. Bestimme für diesen Monat die Anzahl aller verkauften Fahrräder.
(2 P)
c2)
Der Anteil der Mountainbikes lag im Mai und Juni insgesamt bei  im Juli war er größer als im Mai und im August größer als im Juni. Entscheide, ob es dennoch möglich ist, dass der Anteil der Mountainbikes im Juli und August insgesamt kleiner war als insgesamt im Mai und Juni. Begründe deine Entscheidung.
im Juli war er größer als im Mai und im August größer als im Juni. Entscheide, ob es dennoch möglich ist, dass der Anteil der Mountainbikes im Juli und August insgesamt kleiner war als insgesamt im Mai und Juni. Begründe deine Entscheidung.
(3 P)
d)
Der Händler verkauft  der von ihm verkauften Fahrräder über sein Ladengeschäft
der von ihm verkauften Fahrräder über sein Ladengeschäft  den Rest über sein Onlineportal
den Rest über sein Onlineportal  In beiden Fällen bietet er an, für das gekaufte Fahrrad eine Garantieverlängerung abzuschließen
In beiden Fällen bietet er an, für das gekaufte Fahrrad eine Garantieverlängerung abzuschließen 
d1)
Vervollständige zu diesem Sachverhalt das Baumdiagramm.
Zeige, dass die Wahrscheinlichkeit dafür, dass für ein zufällig ausgewähltes verkauftes Fahrrad eine Garantieverlängerung abgeschlossen wird, kleiner als ist.
ist.
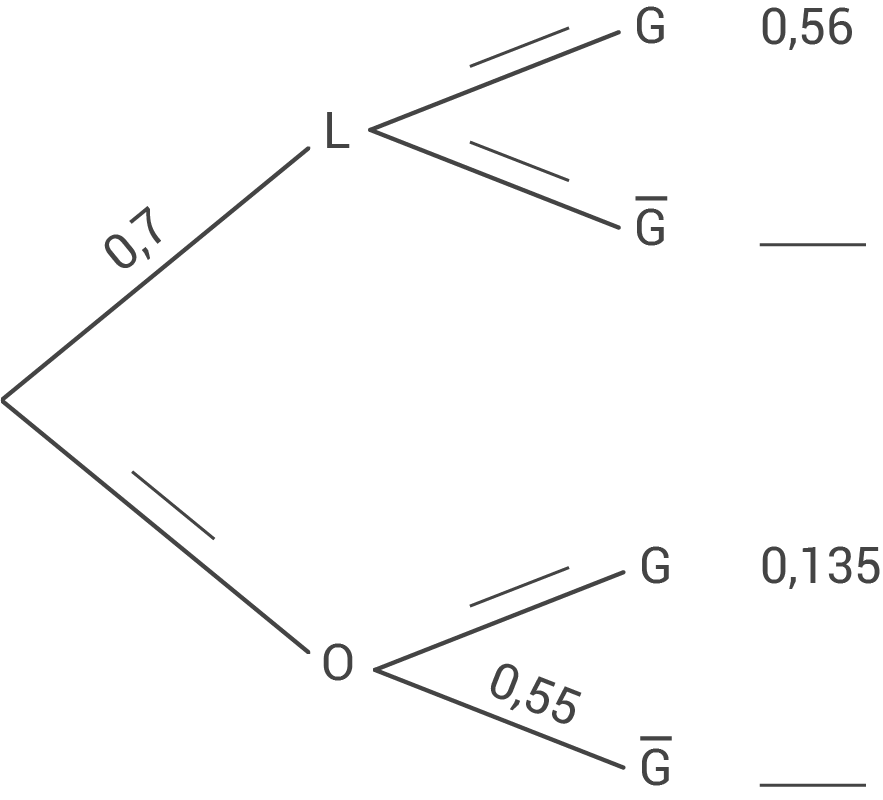
Zeige, dass die Wahrscheinlichkeit dafür, dass für ein zufällig ausgewähltes verkauftes Fahrrad eine Garantieverlängerung abgeschlossen wird, kleiner als

(5 P)
d2)
Nach einer Neugestaltung des Onlineportals vermutet der Händler, dass der Anteil der Fahrräder, für die beim Onlineverkauf eine Garantieverlängerung abgeschlossen wird, auf über  gestiegen ist.
gestiegen ist.
Erstelle einen Hypothesentest mit einer Stichprobengröße von Fahrrädern, der geeignet ist, die Vermutung des Händlers auf einem Signifikanzniveau von
Fahrrädern, der geeignet ist, die Vermutung des Händlers auf einem Signifikanzniveau von  zu stützen. Gib auch die Entscheidungsregel an.
zu stützen. Gib auch die Entscheidungsregel an.
Erstelle einen Hypothesentest mit einer Stichprobengröße von
(8 P)
e)
Betrachtet werden zwei Ereignisse  und
und  eines Zufallsexperiments, deren Wahrscheinlichkeit jeweils ungleich Null ist.
eines Zufallsexperiments, deren Wahrscheinlichkeit jeweils ungleich Null ist.
Beweise die folgende Aussage: Wenn ist, dann ist auch
ist, dann ist auch 
Beweise die folgende Aussage: Wenn
(3 P)
a1)
Bezeichne mit  die Zufallsgröße, welche die zufällige Anzahl an verkauften Mountainbikes in der Stichprobe beschreibt. Laut Aufgabenstellung soll
die Zufallsgröße, welche die zufällige Anzahl an verkauften Mountainbikes in der Stichprobe beschreibt. Laut Aufgabenstellung soll  als binomialverteilt angenommen werden. Die zugehörigen Parameter sind
als binomialverteilt angenommen werden. Die zugehörigen Parameter sind  und
und 
![\(\begin{array}[t]{rll}
P(X=30)&=& B_{100;0,4}(30) &\quad \scriptsize \\[5pt]
&\approx& 0,0100 &\quad \scriptsize \\[5pt]
&=& 1\,\%
\end{array}\)](https://mathjax.schullv.de/03af681fbb051ad51705338698f52fdb8440103e410bbe96d5e97a0c2df48fe8?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  sind genau 30 der verkauften Fahrräder Mountainbikes.
sind genau 30 der verkauften Fahrräder Mountainbikes.
![\(\begin{array}[t]{rll}
P(35\leq X\leq 44)&=& F_{100;0,4}(44)-F_{100;0,4}(34) &\quad \scriptsize \\[5pt]
&\approx& 0,8211-0,1303=0,6908 &\quad \scriptsize \\[5pt]
&=& 69,08\,\%
\end{array}\)](https://mathjax.schullv.de/6988ec6cb3cbaa2b7e1767dfe2b329c01b145ed3387938032a7fceed1dc28063?color=5a5a5a) Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  sind mindestens 35 und weniger als 45 der verkauften Fahrräder Mountainbikes.
sind mindestens 35 und weniger als 45 der verkauften Fahrräder Mountainbikes.
a2)
a3)
Betrachtet man die Formel zur Binomialverteilung  lassen sich aus dem Term die Werte
lassen sich aus dem Term die Werte  und
und  ablesen.
ablesen.  ist noch aus dem Sachzusammenhang bekannt.
ist noch aus dem Sachzusammenhang bekannt.
Subtrahiert von wird in diesem Ereignis aufgezeigt, mit welcher Wahrscheinlichkeit, in einer Stichprobengröße von 10 Fahrrädern, mindestens zwei Mountainbikes verkauft werden.
wird in diesem Ereignis aufgezeigt, mit welcher Wahrscheinlichkeit, in einer Stichprobengröße von 10 Fahrrädern, mindestens zwei Mountainbikes verkauft werden.
Subtrahiert von
a4)
Gesucht ist das kleinste  für das
für das  gilt. Durch systematisches Probieren im Taschenrechner liefert
gilt. Durch systematisches Probieren im Taschenrechner liefert  und
und  .So erkennt man, dass er davon ausgeht, mindestens 2100 Fahrräder zu verkaufen (
.So erkennt man, dass er davon ausgeht, mindestens 2100 Fahrräder zu verkaufen ( ).
).
b)
Wir definieren die Ereignisse, dass ein Mountainbike  und ein Fahrrad mit Aluminiumrahmen
und ein Fahrrad mit Aluminiumrahmen  verkauft wird. Wird ein Fahrrad, das weder ein Mountainbike ist und ohne Aluminiumrahmen, verkauft, definiert sich dies über die Gegenwahrscheinlichkeit
verkauft wird. Wird ein Fahrrad, das weder ein Mountainbike ist und ohne Aluminiumrahmen, verkauft, definiert sich dies über die Gegenwahrscheinlichkeit  Gegeben ist
Gegeben ist 
 und
und  Gesucht ist
Gesucht ist 










 Mit einer Wahrscheinlichkeit von
Mit einer Wahrscheinlichkeit von  besitzt ein verkauftes Mountainbike einen Aluminiumrahmen.
besitzt ein verkauftes Mountainbike einen Aluminiumrahmen.
 |
|||||||||
 |
 |
||||||||
c1)
c2)
Es ist möglich.
Wurden beispielsweise im Juli Fahrräder verkauft und im August
Fahrräder verkauft und im August  so ergibt sich für diese beiden Monate insgesamt für den Anteil der verkauften Mountainbikes
so ergibt sich für diese beiden Monate insgesamt für den Anteil der verkauften Mountainbikes

Wurden beispielsweise im Juli
d1)
 |
|||||||||
 |
 |
||||||||
d2)
Bezeichne mit  die Zufallsgröße, welche die Anzahl der online verkauften Fahrräder mit einer Garantieverlängerung beschreibt. Diese kann als binomialverteilt mit
die Zufallsgröße, welche die Anzahl der online verkauften Fahrräder mit einer Garantieverlängerung beschreibt. Diese kann als binomialverteilt mit  und unbekanntem
und unbekanntem  angenommen werden.
Es soll die Hypothese
angenommen werden.
Es soll die Hypothese  gestützt werden.
gestützt werden.
Als Nullhypothese wird also gewählt.
gewählt.
Gilt der extremste Wert der Nullhypothese, dann ist Wird die Nullhypothese für diesen Wert bei einem rechtsseitigen Test verworfen, so auch für alle anderen möglichen Werte von
Wird die Nullhypothese für diesen Wert bei einem rechtsseitigen Test verworfen, so auch für alle anderen möglichen Werte von  der Nullhypothese.
der Nullhypothese.
Zu bestimmen ist die kleinste natürliche Zahl mit
mit


 Aus
Aus  und
und  ergibt sich
ergibt sich  Somit ist
Somit ist  Wird also für midestens
Wird also für midestens  der
der  Fahhräder beim Onlinekauf eine Garantieverlägerung abgeschlossen, so wird die Nullhypothese abgelehnt und die Vermutung des Händlers gestützt.
Fahhräder beim Onlinekauf eine Garantieverlägerung abgeschlossen, so wird die Nullhypothese abgelehnt und die Vermutung des Händlers gestützt.
Als Nullhypothese wird also
Gilt der extremste Wert der Nullhypothese, dann ist
Zu bestimmen ist die kleinste natürliche Zahl
e)
Die Ereignisse  und
und  sind voneinander unabhängig, da
sind voneinander unabhängig, da  Die Wahrscheinlichkeit von Ereignis
Die Wahrscheinlichkeit von Ereignis  ändert sich nicht, wenn
ändert sich nicht, wenn  eintritt oder nicht. Da
eintritt oder nicht. Da  unabhängig von
unabhängig von  ist, ist ein nicht eintreffen von
ist, ist ein nicht eintreffen von  ebenfalls unabhängig von
ebenfalls unabhängig von  da
da 