Analysis 2

Ein digitales Messgerät misst bei einem Diabetes-Patienten kontinuierlich den Glukosewert (Blutzuckerwert). Der Glukosewert dieses Patienten wird in Abhängigkeit von der Zeit $t$ im Intervall [0; 3,75] mit Hilfe der Funktion $g$ mit

$g(t)=13\cdot t^3-78\cdot t^2+104\cdot t+96$

modelliert. Dabei wird der Glukosewert $g(t)$ in $u$ (Units) und die Zeit $t$ in $h$ (Stunden) seit Messbeginn angegeben. Die Abbildung 1 zeigt den Graphen von $g$ im betrachteten Intervall.

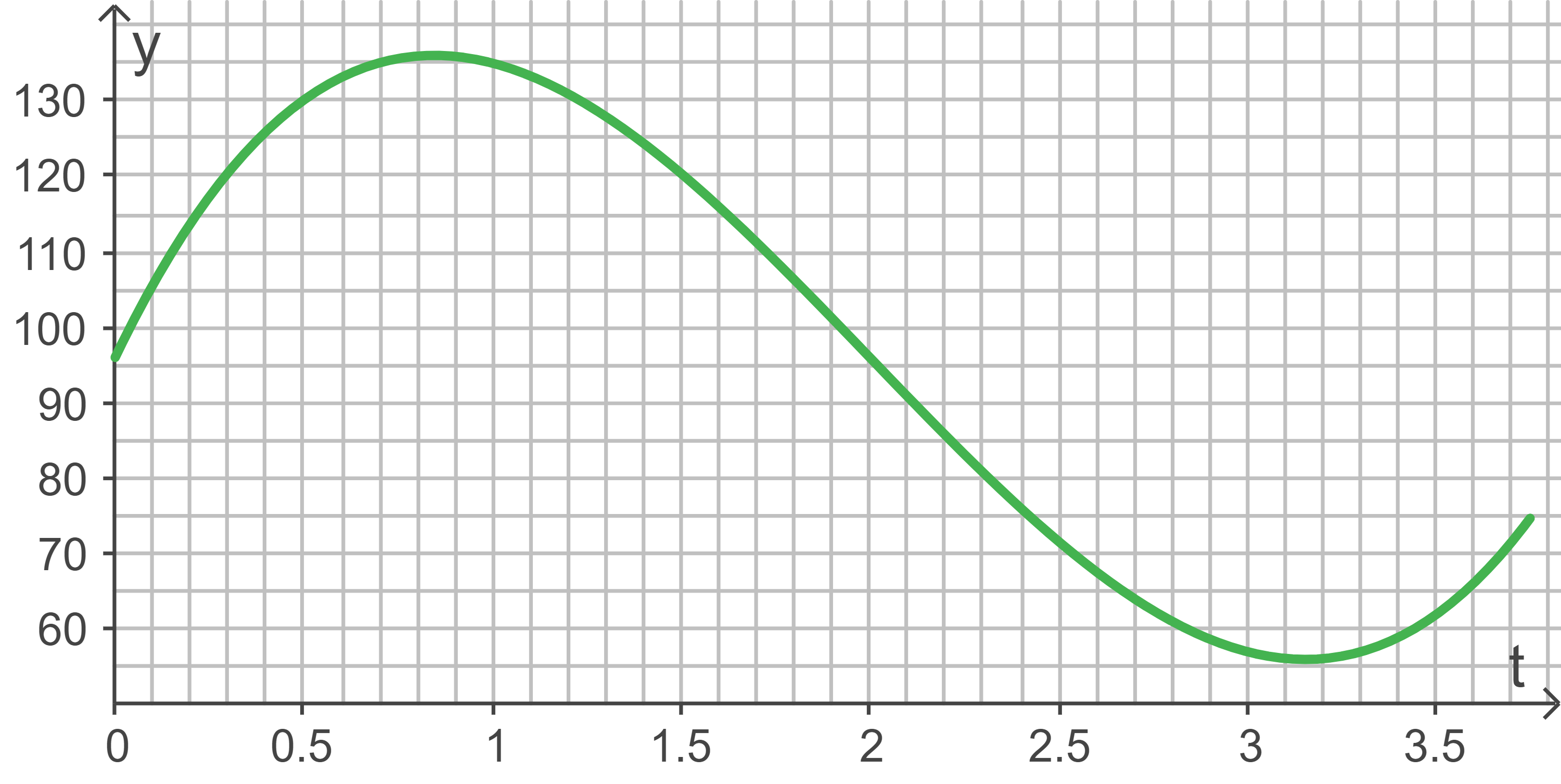
Graph mit einer grünen Kurve, die schwankende Werte auf einem Koordinatensystem darstellt.

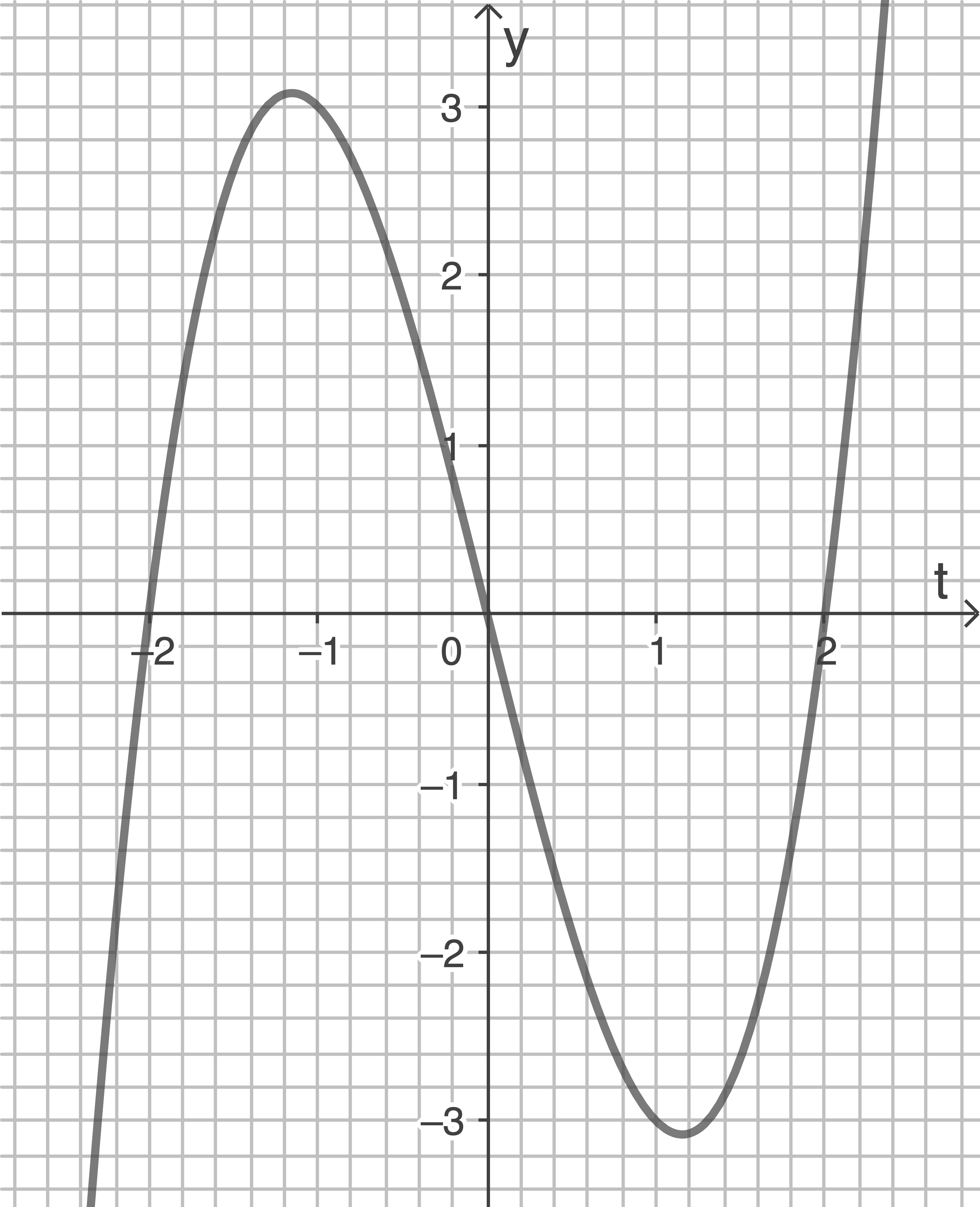
Abbildung 1

a1)

Bei einem Glukosewert von unter $70\,u$ spricht man von Unterzuckerung. Bestimme mit Hilfe des Graphen die Länge des Zeitraums, in dem Unterzuckerung vorliegt.

(2 P)

a2)

Etwas mehr als drei Stunden nach Messbeginn liegt im Bereich der Unterzuckerung der niedrigste Glukosewert. Berechne den zugehörigen Zeitpunkt.

a3)

Weise nach, dass der Glukosewert eine Stunde nach Messbeginn um mehr als 40 % größer ist als zu Beginn der Messung.

(3 P)

a4)

Berechne den durchschnittlichen Glukosewert innerhalb der ersten zwei Stunden nach Messbeginn.

(3 P)

Aus medizinischer Sicht ist ein zu schnelles Absinken des Glukosewerts gefährlich.

b1)

$T(2\mid-52)$ ist der tiefste Punkt des Graphen der Ableitungsfunktion $\(g$ über dem Intervall $[0; 3,75].$
Interpretiere dies im Sachzusammenhang.

(3 P)

b2)

Die folgenden Terme beschreiben unterschiedliche Änderungsarten der Funktion $g$ .

Term A: $\dfrac{g(3)-g(1)}{3-1}$

Term B: $\lim\limits_{h\to0}\dfrac{g(1+h)-g(1)}{h}$

Gib an, welche Änderungsraten diese beiden Terme beschreiben.

(4 P)

b3)

Liegt die momentane Änderungsrate unter einem Wert von $-40\,u/h$ , so zeigt das Messgerät des Patienten ein Warnsymbol an.

Weise nach, dass dieses Warnsymbol im betrachteten Zeitintervall mehr als eine Stunde lang angezeigt wird.

(4 P)

Gegeben ist die Funktionenschar $f_a$ mit

$f_a(t)=a\cdot(t^3-4\cdot t)$ und $a\gt0$ .

Die Abbildung 2 zeigt den Graphen von $f_1$ .

Graph einer Funktion auf einem Koordinatensystem mit x- und y-Achse.

c1)

Für jedes $a\gt0$ hat der Graph von $f_a$ genau einen Hochpunkt $H_a$ . Beschreibe, wie sich die Lage von $H_a$ ändert, wenn sich der Wert des Parameters $a$ verdreifacht.

(3 P)

c2)

Die Tangente an den Graphen von $f_a$ im Punkt $(2\mid 0)$ schließt mit der $t$ -Achse einen Winkel ein.
Bestimme denjenigen Wert für $a$ , für den dieser Winkel 45° beträgt.

(3 P)

c3)

Weise durch Rechnung nach:
Verschiebt man den Graphen von $g$ nach links entlang der $t$ -Achse um 2 Einheiten und anschießend entlang der $y$ -Achse nach unten um 96 Einheiten, so erhält man einen Graphen, der zur Schar $f_a$ gehört.

(5 P)

Gegeben ist die Funktionenschar $h_a$ mit $h_a(t)=-a\cdot t$ und $a\gt0$ .
Betrachtet wird der folgende Term:

$\,\bigg \vert \,\displaystyle\int_{1}^{t_0}f_a(t)\;\mathrm dt\,\bigg \vert\,-\,\bigg \vert \,\displaystyle\int_{1}^{t_0}h_a(t)\;\mathrm dt\,\bigg \vert \,$

Dabei ist $t_0$ diejenige Lösung der Gleichung $f_a(t)=h_a(t)$ , für die $1\lt t_0\lt2$ gilt.

d1)

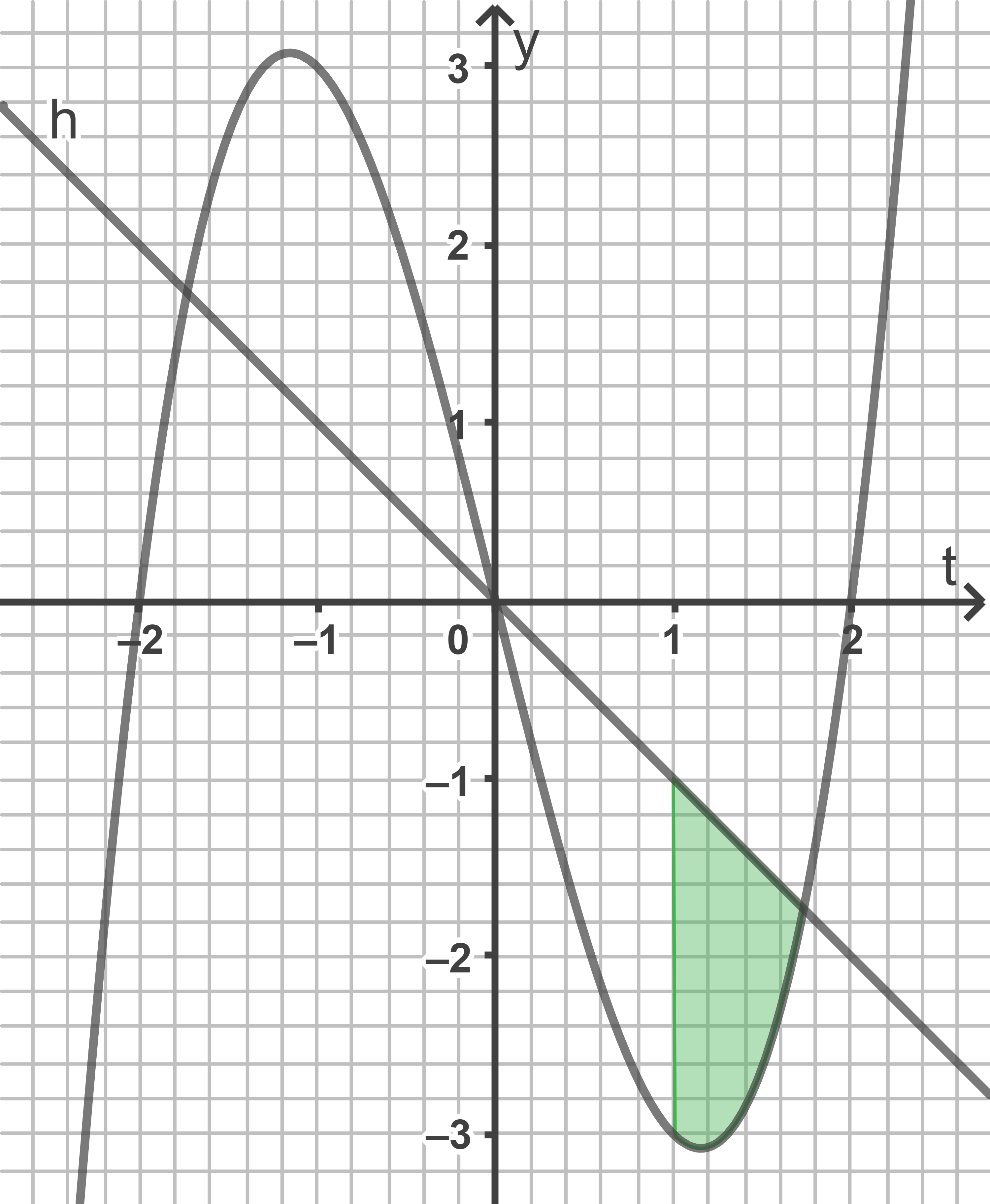
Zeichne in Abbildung 2 ein Flächenstück ein, dessen Inhalt mit dem angegebenen Term für $a=1$ berechnet werden kann.

(2 P)

d2)

Berechne $t_0$ sowie den Wert des obigen Terms in Abhängigkeit von $a$ .

(5 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

Am Graphen kann abgelesen werden, dass der Glukosewert ungefähr zwischen $2,55$ Stunden und $3,68$ Stunden unterhalb von $70\;\text{u}$ liegt.
Somit ist der Patient ca. $1,13$ Stunden lang unterzuckert.

a2)

Um im Bereich der Unterzuckerung den geringsten Glukosewert zu ermitteln, muss das lokale Minimum berechnet werden.

1. Schritt: Ableitung berechnen

$g(t)=13\cdot t^3-78\cdot t^2+104\cdot t+96$

$\(g$

2. Schritt: Notwendige Bedingung für Extremstellen anwenden

$\(\begin{array}[t]{rll} g$

Mit der $pq$ -Formel folgt:

$t_{1/2}=-\dfrac{-4}{2} \pm \sqrt{\left(\dfrac{-4}{2}\right)^2-\dfrac{8}{3}}$

$t_1=3,15\quad t_2=0,85$

Nur $t_1$ liegt im Bereich der Unterzuckerung. Der niedrigste Glukosewert ist somit nach $3,15$ Stunden erreicht.

a3)

$g(0)=96$

$g(1)=13-78+104+96=135$

$\dfrac{135}{96}=1,406\mathrel{\widehat{=}}140,6\%$

Somit ist der Glukosewert nach einer Stunde um $40,6\%$ größer als zu Beginn der Messung.

a4)

Hierzu wird der Mittelwert berechnet:

Vollständigen Rechenweg anzeigen

$\dfrac{1}{2-0}\displaystyle\int_{0}^{2}g(t)\;\mathrm dt=122$

Der durchschnittliche Glukosewert liegt in den ersten beiden Stunden bei $122.$

b1)

Nach genau zwei Stunden sinkt der Glukosewert im gegebenen Intervall am stärksten. Die momentane Änderungsrate beträgt dort $-52\,\text{u/h}.$

b2)

Term A gibt die mittlere Änderungsrate des Glukosewerts im Intervall $[1;3]$ an.
Term B gibt die momentane Änderungsrate des Glukosewertes bei $t=1$ an.

b3)

$\(\begin{array}[t]{rll} g$

Mit der $pq$ -Formel folgt:

$t_{1/2}-\dfrac{-4}{2} \pm \sqrt{\left(\dfrac{-4}{2}\right)^2-\dfrac{144}{39}}$

$t_1\approx2,55\quad t_2\approx1,45$

Wegen $2,55-1,45=1,1\gt1$ wird das Warnsymbol mehr als eine Stunde lang angezeigt.

c1)

1. Schritt: Ableitung berechnen

$\begin{array}[t]{rll} f_a(t)&=& a\cdot (t^3-4 t) \\[5pt] &=& a t^3-4at \end{array}$

$\(f$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} f$

3. Schritt: Veränderung der Lage von $H_a$ ber Verdreifachung von $a$

Da $t$ nicht von $a$ abhängig ist, ändert sich die Stelle des Hochpunkts für kein $a.$

Der Abbildung kann entnommen werden, dass sich der Hochpunkt $H_a$ somit für alle $a$ an der Stelle $t=-\sqrt{2}$ befindet.

Für den $y$ -Wert von $H_a$ gilt:

Vollständigen Rechenweg anzeigen

$f_a(-\sqrt{2})= 2\cdot \sqrt{2} \cdot a$

Bei einer Verdreifachung von $a$ verändert sich der $t$ -Wert der Hochpunkte nicht. Der $y$ -Wert der Hochpunkte hängt dagegen von $a$ ab und wird somit verdreifacht.

c2)

Zunächst wird die Steigung von $f_a(t)$ an der Stelle $t=2$ berechnet:

$\(\begin{array}[t]{rll} f_a$

Mit $\tan(45°)=1$ gilt:

$\(\begin{array}[t]{rll} f$

Für $a=\dfrac{1}{8}$ beträgt der gesuchte Winkel $45^{\circ}.$

c3)

Vollständigen Rechenweg anzeigen

$g^*(t)=f_{13}(t)$

Damit gehört $g^*$ zur Funktionenschar $f_a.$

d1)

Graph einer Funktion mit einer grünen Fläche zwischen den Kurven. Achsen sind beschriftet.

d2)

$t_0$ berechnen

$\begin{array}[t]{rll} f_a(t) &=& h_a(t) \\[5pt] a\cdot(t^3-4t) &=& -at \\[5pt] at^3-4at&=& -at &\quad \scriptsize \mid\; +at \\[5pt] at^3 &=& 3at &\quad \scriptsize \mid\; :at \\[5pt] t^2 &=& 3 &\quad \scriptsize \mid\; \sqrt{} \\[5pt] t&=& \pm \sqrt{3} \end{array}$

Da $1\lt t_0 \lt2$ gelten muss, ist $t_0=\sqrt{3}.$

Wert des Terms berechnen

Vollständigen Rechenweg anzeigen

$\,\bigg \vert \,\displaystyle\int_{1}^{t_0}f_a(t)\;\mathrm dt\,\bigg \vert \,-\,\bigg \vert \,\displaystyle\int_{1}^{t_0}h_a(t)\;\mathrm dt\,\bigg \vert \, =a$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?