Analytische Geometrie

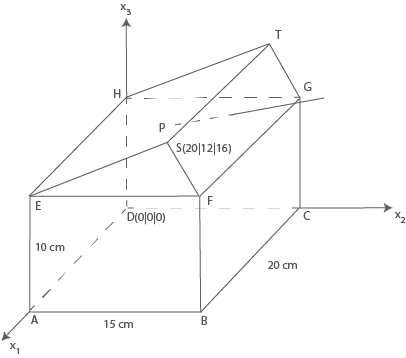
In einer Miniaturausstellung ist das Modell einer Seilbahn mit einer Gondel aufgebaut. Die Abbildung zeigt die Talstation, die die Form eines Quaders mit einem aufgesetzten Prisma hat. Sie steht auf der Grundfläche der Ausstellung, die in der $x_1x_2$ -Ebene liegt. Eine Einheit entspricht einem Zentimeter in der Wirklichkeit.

3D-Diagramm eines Quaders mit Koordinaten und Abmessungen in cm.

Abb. 1

Gib die Koordinaten der Punkte $A$ , $F$ , $G$ und $T$ an und bestimme eine Koordinatenform der Dachebene $E_1$ , die die Punkte $F$ , $G$ und $S$ enthält.

$E_1: 2x_2+x_3=40$

Das Seil der Seilbahn ist geradlinig zwischen den Punkten $P(6\;|\;5\;|\;12)$ und $Q(38\;|\;133\;|\;44)$ (außerhalb der Abbildung) gespannt. Ermittle die Koordinaten des Punktes $R$ , in dem das Seil die Dachebene $E_1$ durchstößt.
Berechne die Länge und den Steigungswinkel des Seils.

(14P)

In der Ausstellung ist eine zweite Seilbahn installiert. Das Seil dieser Bahn ist im Punkt $K(61\;|\;81\;|\;0)$ befestigt und verläuft in Richtung des Vektors $\overrightarrow{v}=\pmatrix{-2\\-2\\1}$ .

Zeige, dass sich die Geraden, entlang derer die Seile verlaufen, nicht schneiden.
Berechne den Abstand dieser Geraden voneinander.

(9P)

Bei der ersten Seilbahn ist eine kugelförmige Gondel so am Seil befestigt, dass ihr Mittelpunkt die Koordinaten $M(10\;|\;21\;|\;13,5)$ hat. Die Gondel hat einen Durchmesser von $4\,\text{cm}$ und ist aus Plexiglas hergestellt.

Gib eine Gleichung der Kugel $K$ an, die die Gondel beschreibt.

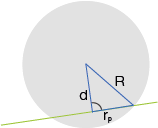
In der Gondel sollte eine kreisförmige Plattform parallel zur Grundfläche positioniert werden. Beim Einkleben ist die Plattform verrutscht; sie liegt jetzt in der Ebene

$E_2: 19x_1+180x_3=2.292,39$

Ein einfaches Diagramm einer Wippe mit einem Kreis und einer horizontalen Linie.

Abb. 2

An der Gondel ist ein Schild mit einem Firmenlogo angebracht worden, sodass es die Gondel tangential in einem Punkt $Y$ berührt und von schräg oben lesbar ist. Ein Normalenvektor zu der Schildebene ist $\overrightarrow{j}=\pmatrix{1\\0\\1}$ .

$Y$

(13P)

Gegeben seien zwei windschiefe Geraden $k$ und $l$ mit $k : \overrightarrow{x}=\pmatrix{6\\5\\12}+t\cdot\pmatrix{1\\4\\1}$ und $l : \overrightarrow{x}=\pmatrix{61\\81\\0}+s\cdot\pmatrix{-2\\-2\\1}$ . Es gibt einen Punkt $U$ auf $k$ und einen Punkt $V$ auf $l$ , so dass der Vektor $\overrightarrow{UV}$ senkrecht zur $x_1x_2$ -Ebene ist.

Ermittle die Koordinaten der Punkte $U$ und $V$ .

(4P)

Bildnachweise [nach oben]

[1]

[2]

Aufgabe A3

$\blacktriangleright$ Koordinaten der Eckpunkte bestimmen

In dieser Aufgabe sind die Eckpunkte $A,F,G,T$ eines Gebäudemodells zu berechnen. Zur Bestimmung dieser Punkte nutzt du, dass du Vektoren paralleler Seiten ersetzen kannst. Berechne so $\overrightarrow{OA}$

$\overrightarrow{OA} = \overrightarrow{0} + \pmatrix{20\\0\\0} = \pmatrix{20\\0\\0}$

$\overrightarrow{OF} = \overrightarrow{OA} + \overrightarrow{AE} + \overrightarrow{EF} = \pmatrix{20\\0\\0} + \pmatrix{0\\0\\10} + \pmatrix{0\\15\\0} = \pmatrix{20\\15\\10}$

Für $\overrightarrow{OG}$ gilt

$\overrightarrow{OG} = \overrightarrow{OF} + \overrightarrow{FG} = \pmatrix{20\\15\\10} - \pmatrix{20\\0\\0} = \pmatrix{0\\15\\10}$

Für $\overrightarrow{OT}$ gilt

$\overrightarrow{OT} = \overrightarrow{OG} + \overrightarrow{FP} = \pmatrix{0\\15\\10} + \pmatrix{20 - 20 \\ 12 - 15 \\ 16 - 10} = \pmatrix{0\\12\\16}$

Somit lauten die Koordinaten der Punkte

$A(20 \mid 0 \mid 0)\, ; F(20 \mid 15 \mid 10) \, ; G(0\mid 15\mid 10) \, ; T(0\mid 12 \mid 16)$

$\blacktriangleright$ Ebenengleichung der Dachebene bestimmen

Nun sollst du die Koordinatenform der Gleichung der Dachebene finden, die die Punkte $F,G,S$ enthält.

Für die Koordinatenform berechnest du zunächst die Parametergleichung der Dachebene. Benutze dazu die allgemeine Gleichung für eine Ebene in Parameterform:

$E: \overrightarrow{x} = \overrightarrow{p} + r \cdot \overrightarrow{u} + s \cdot \overrightarrow{v}$

Als Stützvektor $\overrightarrow{p}$ kannst du $\overrightarrow{OF}$ wählen, als Richtungsvektoren $\overrightarrow{u}$ , $\overrightarrow{v}$ die Vektoren $\overrightarrow{FP}$ und $\overrightarrow{FG}$ .

Du erhältst also

$E_1: \overrightarrow{x} = \pmatrix{20\\15\\10} + r \cdot \pmatrix{0\\-3\\6} + s \cdot \pmatrix{20\\0\\0}$

Um aus der Parametergleichung eine Gleichung in Koordinatenform zu erhalten, musst du einen Normalenvektor der Ebene finden. Dies tust du, indem du das Kreuzprodukt der Richtungsvektoren berechnest

$\pmatrix{0\\-3\\6} \times \pmatrix{20\\0\\0} = \pmatrix{0\\120\\60}$

Durch Divison durch $60$ kannst du den Normalenvektor kürzen:

$\overrightarrow{n} = \pmatrix{0\\2\\1}$

Mithilfe einer Punktprobe ergibt sich:

$\begin{array}[t]{rll} E_1:\quad 2x_2 + x_3 &=& d \\[5pt] 2\cdot 15 + 10&=& d \\[5pt] 40&=& d \end{array}$

Die Koordinatenform lautet also:

$E_1: 2x_2 + x_3 = 40$

$\blacktriangleright$ Koordinaten des Durchstoßpunktes bestimmen

Um die Koordinaten des Punktes $R$ zu ermitteln, in dem das Seil die Dachebene durchstößt, musst du den Schnittpunkt einer Geraden mit der Dachebene bestimmen. Die Gerade modelliert den Verlauf des Seils.

Stelle zunächst die Gleichung für die Gerade auf und verwende $\overrightarrow{OP}$ als Stützvektor und $\overrightarrow{PQ}$ als Richtungsvektor.

$h: \overrightarrow{x} = \pmatrix{6\\5\\12} + m \cdot \pmatrix {38 - 6 \\ 133 - 5 \\ 44 - 12} = \pmatrix{6\\5\\12} + m \cdot \pmatrix {32 \\ 128 \\ 32}$

Nutze jetzt, dass du den Richtungsvektor mit einer Zahl multiplizieren kannst. Klammere also $\dfrac{1}{32}$ aus dem Richtungsvektor aus, setze $r = \dfrac{1}{32} \cdot m$ und du erhältst.

$g: \overrightarrow{x} = \pmatrix{6\\5\\12} + r \cdot \pmatrix {1 \\ 4 \\ 1}$

Setze jetzt $\overrightarrow{g}$ in die Koordinatenform der Ebenengleichung ein und löse diese Gleichung nach $r$ auf

$\begin{array}[t]{rll} &2 \cdot (5 + 4r) + 12 + r &=& 40 &\quad \scriptsize \mid\; -22 \\[5pt] &9r&=&18 & \quad \scriptsize \mid\; : 9 \\[5pt] &r &=& 2& \end{array}$

Setze nun $r=2$ in die Geradengleichung $\overrightarrow{g}$ ein und du erhältst

$\overrightarrow{OR} = \pmatrix{8\\13\\14}$

Somit lauten die Koordinaten des Punktes $R$ $(8 \mid \ 13 \mid 14)$ .

$\blacktriangleright$ Länge des Seils berechnen

Die Länge des Seils ist gerade der Betrag des Vektors $\overrightarrow{PQ}$ . Das ist also

$\vert \overrightarrow{RQ} \vert = \sqrt{32^2+128^2+32^2} \approx 135,76$

Da eine Längeneinheit einem Zentimeter in der Wirklichkeit entspricht, beträgt die Länge des Seils $135,76 \, \text{cm}$ .

$\blacktriangleright$ Steigungswinkel des Seils berechnen

Der Steigungswinkel des Seils entspricht gerade dem Winkel, den die Gerade $g$ mit der $x_1,x_2$ - Ebene einschließt. Um diesen Winkel zu erhalten, benutzt du die Formel

$\mathrm{sin}(\alpha) = \dfrac{ \vert \overrightarrow{n} \cdot \overrightarrow{p} \vert }{ \vert \overrightarrow{n} \vert \cdot \vert \overrightarrow{p} \vert}$

Darin ist $\overrightarrow{n}$ ein Normalenvektor der $x_1,x_2$ - Ebene. $\overrightarrow{p}$ ist ein Richtungsvektor der Geraden, die das Seil darstellt.

Als Normalenvektor kannst du $\pmatrix{0\\0\\1}$ wählen. Rechne also

$\begin{array}[t]{rll} \mathrm{sin}(\alpha)&=& \dfrac{1 }{ \sqrt{1^2} \cdot \sqrt{1^2+4^2+1^2}}&\quad \scriptsize \\[5pt] \mathrm{sin}(\alpha)&\approx& 0,24 &\quad \scriptsize \\[5pt] \alpha&\approx& 13,63^{\circ} &\quad \scriptsize \\[5pt] \end{array}$

Folglich berechnet sich der Steigungswinkel des Seils zu $13,63^{\circ}$ .

$\blacktriangleright$ Fehlen eines Schnittpunktes zeigen

Nun wird eine zweite Seilbahn installiert. Du musst nachweisen, dass das Seil dieser neuen Seilbahn das Seil der alten Seilbahn nicht schneidet.

Stelle dazu zuerst eine neue Geradengleichung auf. Als Stützvektor wählst du den Ortsvektor des gegebenen Punktes $K$ und der Richtungsvektor war gegeben.

$f: \overrightarrow{x} = \pmatrix{61\\81\\0} + s \cdot \pmatrix{-2\\-2\\1}$

Um nachzuweisen, dass die Geraden $g$ und $f$ keinen Schnittpunkt haben, musst du zeigen, dass sich keine eindeutigen Lösungen für die beiden Parameter $r$ und $s$ ergeben, wenn du die Gleichung von $g$ mit der Gleichung von $f$ gleichsetzt.

$\begin{array}{} 61 - 2s&=&6 + r\quad\\ 81 -2s&=& 5 + 4r \quad\\ s&=& 12 + r \quad\\ \end{array}$

Die letzte Gleichung ist bereits der Wert für $s$ . Setze diesen in die erste Gleichung ein und du erhältst:

$\begin{array}[t]{rll} 61 - 2 \cdot (12 + r)&=&6 + r &\quad \scriptsize \mid\;-r -37 :(-3) \\[5pt] r&=&\dfrac{-31}{3}& \end{array}$

Setze $s$ in die dritte Gleichung ein und du erhältst

$\begin{array}[t]{rll} &81 - 2 \cdot (12 + r)&=&6 + r &\quad \scriptsize \mid\;-r -67 :(-3) \\[5pt] &r&=&\dfrac{-61}{3}& \end{array}$

Somit erhältst du zwei unterschiedliche Lösungen für $r$ und damit sind die Geraden $g$ und $f$ nicht parallel.

$\blacktriangleright$ Abstand der beiden Geraden berechnen

Um den Abstand zweier Geraden zu berechnen, musst du prüfen, wie diese zueinander liegen. Da sich $g$ und $f$ nicht schneiden, können sie zueinander parallel oder windschief sein.

Wenn zwei Geraden zueinander parallel sind, sind ihre Richtungsvektoren $\overrightarrow{u}$ und $\overrightarrow{v}$ voneinander linear abhängig. Wähle also

$g: \overrightarrow{a} + r \cdot \overrightarrow{u}$

$f: \overrightarrow{b} + s \cdot \overrightarrow{v}$

Prüfe die Parallelität mit

$\overrightarrow{u} = k \cdot \overrightarrow{v}$

$\pmatrix{1\\4\\1} = k \cdot \pmatrix {-2\\-2\\1}$

Diese Gleichung führt zu einem Widerspruch. Aus der ersten Komponente erhältst du $k = -\dfrac{1}{2}$ und die dritte Komponente liefert $k = 1$ . Folglich sind die Geraden $g$ und $f$ windschief, da sie einander weder schneiden noch parallel sind.

Den Abstand zweier windschiefer Geraden berechnest du mit der Formel

$d = \dfrac{(\overrightarrow{a} - \overrightarrow{b}) \cdot \overrightarrow{n}} {\vert \overrightarrow{n} \vert}$

Darin ist der Vektor $\overrightarrow{n}$ ein Vektor, der auf den beiden Richtungsvektoren senkrecht steht. $\overrightarrow{a}$ und $\overrightarrow{b}$ sind die Stützvektoren der beiden Geraden.

Berechne also das Kreuzprodukt von $\overrightarrow{u}$ und $\overrightarrow{v}$ .

$\pmatrix{1\\4\\1} \times \pmatrix {-2\\-2\\1} = \pmatrix{6\\-3\\6}$

Damit ergibt sich der Abstand der beiden Geraden zu

$d = \pmatrix{61 - 6\\ 81 - 5 \\ 0 - 12} \cdot \pmatrix{6\\-3\\6} \cdot \dfrac {1} { \sqrt{6^2+(-3)^2+6^2}} = \dfrac{10}{3}$

$\blacktriangleright$ Gleichung angeben, die die Kugel beschreibt

Nun wird eine kugelförmige Gondel an der ersten Seilbahn befestigt. Du sollst nun die Gleichung der Kugel $K$ angeben, die die Gondel beschreibt. Dazu nutzt du, dass die Punkte $\pmatrix{x\\y\\z}$ innerhalb einer Kugel mit Radius $r$ und Mittelpunkt $P{a \mid b \mid c}$ so beschrieben werden können

$K: \sqrt{x-a)^2 + (y-b)^2 + (z-c)^2} \leq r^2$

Der Mittelpunkt war gegeben zu $(10 \mid 21 \mid 13,5)$ und der Radius berechnet sich über die Hälfte des Durchmessers zu $\dfrac{4}{2} = 2$ . Also gilt für die Punkte innerhalb der Kugel $K$

$K: \sqrt{(x-10)^2+(y-21)^2+(z-13,5)^2} \leq 4$

$\blacktriangleright$ Bestimmung des Mittelpunktes der Plattform

Du musst den Mittelpunkt und den Flächeninhalt der verrutschten kreisförmigen Plattform berechnen. Die Plattform ist gerade der Schnittkreis der Ebene $E_2$ mit der Kugel $K$ .

Um die Koordinaten des Mittelpunktes des Schnittkreises zu berechnen, stellst du die Geradengleichung durch den Mittelpunkt der Kugel in Richtung des Normalenvektors der Ebene auf.

$g: \overrightarrow{x} = \pmatrix{10\\21\\13,5} + r \cdot \pmatrix{19\\0\\180}$

Diese Gleichung setzt du nun in die Ebenengleichung für $E_2$ ein

$\begin{array}[t]{rll} 19\cdot (10 + 19r)+180(13,5+180r)&=& 2.292,39 &\quad \scriptsize \; \\[5pt] 2.620 + 32.761r &=& 2.292,39 \\ 2.620 + 32.761r &=& 2.292,39 \\ r &=& -0,01 \\ \end{array}$

Den Wert für $r$ setzt du nun in die Geradengleichung ein und erhältst:

$\pmatrix{10\\21\\13,5} - 0,01 \cdot \pmatrix{19\\0\\180} = \pmatrix{9,81\\21\\11,7}$

Also sind die Koordinaten des Mittelpunktes der Plattform $W(9,81 \mid 21 \mid 11,7)$ .

$\blacktriangleright$ Bestimmung des Flächeninhalts der Plattform

Mache dir zunächst eine Skizze. Daran erkennst du, dass es sich bei dem Dreieck mit den Seiten $r_p,d,R$ um ein rechtwinkliges Dreieck handelt.

Geometrische Darstellung eines Kreises mit Bezeichnungen für Radius, Distanz und Linie.

Abb. 1: Das Dreieck mit den Seiten $r_p,d,R$ ist rechtwinklig

Den Flächeninhalt der Plattform berechnest du mithilfe der Hesschen Normalenform der Ebenengleichung

$E_2 = \dfrac{1}{\sqrt{19^2 + 180^2}} \cdot (19x_1+180x_3) \approx 12.67$

Der Radius $r_P$ entspricht gerade dem Abstand des Mittelpunktes $M$ von der Ebene $E_2$ . Diesen kannst du ermitteln, indem du die Koordinaten des Punktes in die Hessesche Normalenform der Ebene $E_2$ einsetzt

$d = \dfrac{1}{\sqrt{19^2 + 180^2}} \cdot (19 \cdot 10 +180 \cdot 13,5) - 12,67 \approx 1,8$

Verwende nun den Satz des Pythagoras

$r_p^2 = r^2 - d^2 = 4 - 1,8^2 \approx 0,7239$

Somit ergibt sich der Flächeninhalt der Plattform zu $A = \pi \cdot r_p^2 \approx 2,27 \, \text{cm}^2$

$\blacktriangleright$ Berührpunkt berechnen

Um irgendeinen Punkt auf der Kugeloberfläche zu erhalten, musst du vom Mittelpunkt der Kugel zwei Längeneinheiten aus in eine beliebige Richtung gehen. Dann bewegst du dich auf der Kugeloberfläche.

Hier ist die Richtung, in die du gehen musst, durch den Normalenvektor der Tangentialebene vorgegeben. Wenn du den Berührpunkt der Schildebene mit der Kugel bestimmen willst, musst du dich vom Kugelmittelpunkt zwei Längeneinheiten in Richtung des Normalenvektors der Tangentialebene bewegen.

Normiere dazu den Normalenvektor der Ebene und rechne

$\overrightarrow{OY} = \overrightarrow{OM} + 2 \cdot \dfrac{\overrightarrow{j}}{\vert \overrightarrow{j} \vert} = \pmatrix{10\\21\\13,5} + \dfrac{2}{\sqrt{2}} \pmatrix{1\\0\\1} = \pmatrix{10 + \sqrt{2} \\ 21 \\ 13,5 + \sqrt{2}}$

Also hat $Y$ in etwa die Koordinaten $(11,41 \mid 21 \mid 14,91)$ .

$\blacktriangleright$ Koordinaten zweier Punkte ermitteln

Um einen Punkt zu erhalten, der senkrecht zur $x_1,x_2$ Ebene ist, machst du den Ansatz

$\overrightarrow{OP} = a \cdot \pmatrix{0\\0\\1}$

Für diesen Punkt muss gelten: $\overrightarrow{OP} = \overrightarrow{y} - \overrightarrow{x}$

Dabei gilt $\overrightarrow{x} \in k$ und $\overrightarrow{y} \in l$ . Du erhältst also ein Gleichungssystem in den drei Unbekannten $s,t,a$ , die du auflösen musst.

$\begin{array}[t]{rll} -t -2s&=& -55 & \\ -4t -2s&=& -76 \\ -a + t +s &=& 12 \end{array}$

Hier genügt es, wenn du nur die ersten beiden Gleichungen löst, da du aus der Aufgabenstellung schon weißt, dass dieses Gleichungssystem eindeutig lösbar sein muss und da nur die Parameter $s,t$ relevant sind.

Aus der ersten Gleichung erhältst du $t = 55 - 2s$ . Eingesetzt in die zweite Gleichung ergeben sich die Werte $s = 24$ und $t = 7$ . Setze diese Parameter nun in die Geradengleichungen für $k$ und $l$ ein

$\overrightarrow{OU} = \pmatrix{6\\5\\12} + 7 \cdot \pmatrix{1\\4\\1} = \pmatrix{13\\33\\19}$

$\overrightarrow{OV} = \pmatrix{61\\81\\0} + 24 \cdot \pmatrix{-2\\-2\\1} = \pmatrix{13\\33\\24}$

Folglich sind die Koordinaten $U(13 \mid 33 \mid 19)$ , $V(13 \mid 33 \mid 24)$ .

Bildnachweise [nach oben]

[1]