SchulLV Logo
Lerninhalte in Mathe
Abi-Aufgaben (WTR)
Abi-Aufgaben (CAS)
Digitales Schulbuch
Inhaltsverzeichnis

Analysis 2

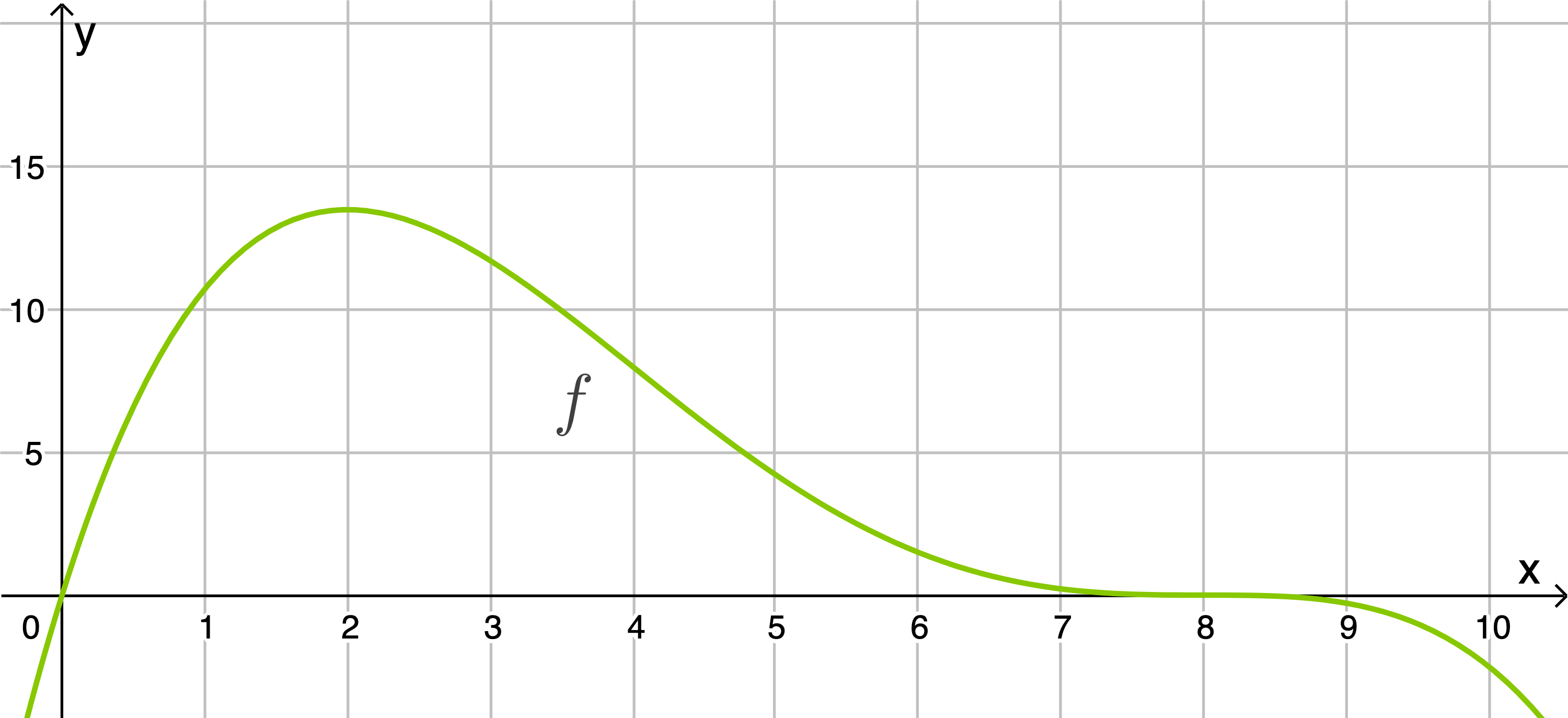
Die Abbildung zeigt den Graphen einer in \(\mathbb{R}\) definierten ganzrationalen Funktion \(f\) vierten Grades. Die Tangente im Wendepunkt \(W(4\mid8)\) des Graphen hat die Steigung \(-4.\)
Graf einer mathematischen Funktion mit einer grünen Kurve im Koordinatensystem.
a)
a1)
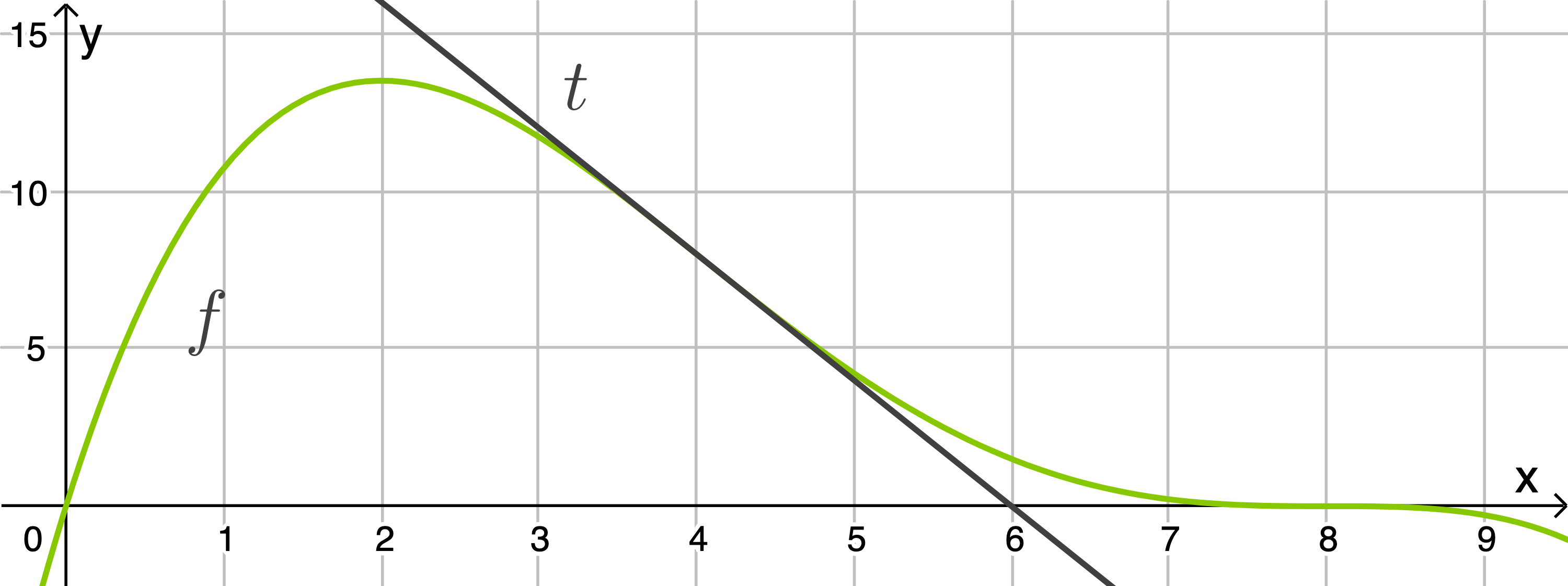
Zeichne die beschriebene Tangente in die Abbildung ein.
Bestimme eine zugehörige Geradengleichung mit Hilfe der gegebenen Werte.
(3 P)
a2)
Die erste Ableitungsfunktion \(f von \(f\) besitzt zwei ganzzahlige Nullstellen.
Gib diese beiden Nullstellen an.
Der Graph von \(f besitzt einen Tiefpunkt.
Gib die Koordinaten dieses Tiefpunkts an, und begründe deine Angabe.
(5 P)
a3)
Die Funktion \(f\) hat eine Gleichung der Form
\(f(x)=ax^4+bx^3+cx^2+16x.\)
Bestimme die Werte der Parameter \(a,\) \(b\) und \(c.\)
[Zur Kontrolle: \(f(x)=-\frac{1}{32}x^4+\frac{3}{4}x^3-6x^2+16x\)]
(6 P)
a4)
Weise rechnerisch nach, dass der Graph von \(f\) an der Stelle \(x=8\) einen Sattelpunkt, d.h. einen Wendepunkt mit waagerechter Tangente, hat.
(4 P)
Am 26. April 1986 ereignete sich in der Ukraine ein Reaktorunfall, bei dem radioaktives Plutonium-241 freigesetzt wurde. Plutonium-241 zerfällt exponentiell, d.h. in jedem Jahr nimmt die Masse des vorhandenen Plutonium-241 um einen konstanten prozentualen Anteil ab. Der Zerfall einer bestimmten Menge Plutonium-241 wird im Folgenden durch die Funktion \(p\) mit
\(p(x)=200\cdot\mathrm e^{-0,048x}\) und \(x\geq0\)
beschrieben. Dabei ist \(x\) die Zeit in Jahren, die seit dem Reaktorunfall vergangen ist, und \(p(x)\) die Masse des verbliebenen Plutonium-241 in Milligramm.
b)
b1)
Gib die Bedeutung des Faktors \(200\) im Sachzusammenhang an.
Berechne den prozentualen Anteil, um den die Masse des Plutonium-241 in jedem Jahr abnimmt.
(3 P)
b2)
Bestimme das Jahr, in dessen Verlauf erstmals weniger als ein Milligramm des Plutonium-241 vorhanden sein wird.
(4 P)
Beim Zerfall eines radioaktiven Stoffs kann ein weiterer radioaktiver Stoff entstehen, der ebenfalls exponentiell zerfällt.
Für ein geeignetes \(k\gt 0\) modelliert die Funktion \(h_k\) mit
\(h_k(x)=10\cdot(1-\mathrm e^{-kx})\cdot\mathrm e^{-x}\) und \(x\geq0\)
die zur Zeit \(x\) vorhandene Masse des neu entstandenen Stoffs. Die Abbildung zeigt den Graphen von \(h_1.\)
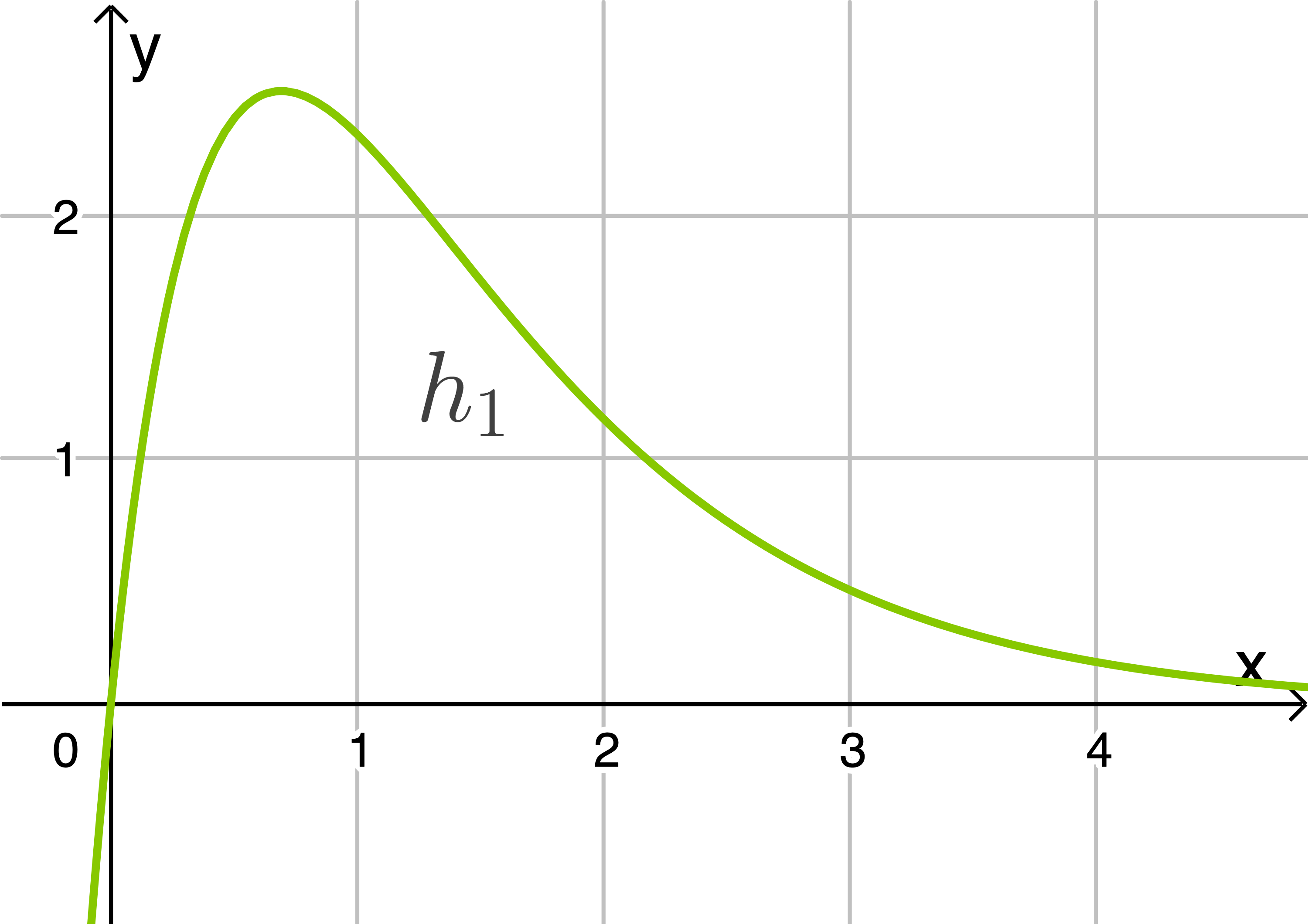
Kurve in grün im Koordinatensystem mit Achsenbeschriftung.
c)
c1)
Zeige, dass \(h_k\) nur die Nullstelle \(x=0\) hat.
(2 P)
c2)
Der Graph der Funktion \(h_k\) hat genau einen Hochpunkt. Für die erste Ableitungsfunktion \(h gilt
\(h
Bestimme die \(x\)-Koordinaten des Hochpunkts in Abhängigkeit von \(k.\)
(3 P)
d)
Beim Zerfall von Plutonium-241 entsteht als weiterer radioaktiver Stoff Americium-241.
Die Funktion \(a\) mit
\(a(x)=207\cdot(1-\mathrm e^{-0,0464x})\cdot\mathrm e^{-0,0016x}\) und \(x\geq0\)
gibt für jedes Jahr \(x\) die Masse des vorhandenen Americium-241 in Milligramm an.
d1)
Der Graph von \(a\) kann für einen Wert von \(k\) aus dem Graphen der Funktion \(h_k\) erzeugt werden, indem man diesen in \(x\)-Richtung und in \(y\)-Richtung streckt.
Gib die beiden Streckungsfaktoren an und bestimme den passenden Wert von \(k.\)
(3 P)
d2)
Im Funktionsterm von \(a\) beschreibt der Faktor \(1-\mathrm e^{-0,0464x}\) die Zunahme der Masse des vorhandenen Americium-241 und der Faktor \(e^{-0,0016x}\) den Zerfall des vorhandenen Americium-241.
Begründe, dass es einen Zeitpunkt gibt, zu dem beide Faktoren den gleichen Wert annehmen, ohne diesen Zeitpunkt zu berechnen.
(3 P)
e)
Für jeden Wert von \(k\) gibt es zu der Funktion \(h_k\) eine Stammfunktion \(H_k\) mit
\(H_k(x)=-10\cdot\mathrm e^{-x}+\dfrac{10}{k+1}\cdot\mathrm e^{-(k+1)x}.\)
Zeige, dass \(\displaystyle\int_{0}^{\infty}h_k(x)\;\mathrm dx \lt10\) für alle \(k\gt0\) gilt.
(4 P)