Analysis 2

Die Pegelhöhe eines Kanals wurde während eines Hochwasserereignisses an einem Ort für einen Zeitraum von 14 Tagen beobachtet. Der zeitliche Verlauf der Pegelhöhe kann näherungsweise durch die Funktion $h$ mit

$h(t)=\frac{3}{2}\cdot \mathrm{e}^{-\frac{1}{18}(t-8)^2}+4$ ; $t\in [0;14]$

beschrieben werden. Diese hat die Ableitungen

$h‘(t)=$	$-\dfrac{1}{6}\cdot (t-8)\cdot \mathrm{e}^{-\frac{1}{18}(t-8)^2}$	und
$h‘‘(t)=$	$\left(\dfrac{1}{54}\left(t-8\right)^2-\dfrac{1}{6}\right) \cdot \mathrm{e}^{-\frac{1}{18}(t-8)^2}$ .

Die Pegelhöhe $h$ wird vom tiefsten Punkt des Kanalbetts bis zur Wasseroberfläche gemessen, $t$ steht für die Zeit nach Beobachtungsbeginn in Tagen und $h(t)$ für die Pegelhöhe in Metern.

Bestimme die mittlere Änderungsrate der Pegelhöhe im Intervall $[0;3]$ .

Leite aus der ersten Ableitung der Funktion $h$ deren zweite Ableitung her.

Berechne die höchsten und die niedrigsten Pegelhöhen im Beobachtungszeitraum.

Berechne die beiden Wendestellen der Funktion $h$ und erläutere deren Bedeutung im Sachzusammenhang. Eine hinreichende Bedingung für die Existenz von Wendestellen muss nicht betrachtet werden.

Skizziere den Graphen der Funktion $h$ .

(19P)

b) Berechne mit Hilfe des Taschenrechners den Ausdruck

$\dfrac{1}{14}\displaystyle\int_{0}^{14}h(t)\;\mathrm dt$

und interpretiere das Ereignis im Sachzusammenhang.

(3P)

Das achsensymmetrische Kanalbett kann über dem Intervall $[-10;10]$ näherungsweise durch eine ganzrationale Funktion $f$ modelliert werden. In jedem der Punkte $(-10\mid 6)$ und $(10\mid 6)$ schließt sich jeweils ein horizontaler Uferweg knickfrei an. Der Ursprung des Koordinatensystems liegt dabei in der Mitte des Kanals im tiefsten Punkt des Kanalbettes.

Diagramm mit einer Funktion und verschiedenen Flächenmarkierungen auf einem Koordinatensystem.

Entscheide, welche Werte für den Grad $k$ der Funktion $f$ gewählt werden können. Begründe deine Entscheidung.

Verwende im Folgenden die Funktion $f$ mit $f(x)=-0,0006\cdot x^4+0,12\cdot x^2$ .
Die normale Pegelhöhe des Kanals beträgt $4\,\text{m}$ .

Zeige, dass die Breite der Wasseroberfläche des Kanals bei normaler Pegelhöhe ca. $13\,\text{m}$ beträgt.

Bei normaler Pegelhöhe hat die wassergefüllte (in der Abbildung grau hinterlegte) Querschnittsfläche des Kanals einen Flächeninhalt von ca. $32,81\,\text{m}^2$ . Bei einer Pegelhöhe von $5,5\,\text{m}$ ist die Wasseroberfläche des Kanals ca. $16,87\,\text{m}$ breit.
Ermittle, um wie viel Prozent sich der Flächeninhalt der wassergefüllten Querschnittsfläche des Kanals vergrößert, wenn der Pegel von normaler Pegelhöhe bis auf die Pegelhöhe von $5,5\,\text{m}$ ansteigt.

(14P)

d) Es gibt eine Funktion $b$ , die jedem Zeitpunkt $t$ des Beobachtungszeitraums eine Breite der Wasseroberfläche des Kanals zuordnet. Dabei wird die Breite in Metern betrachtet.
Zeige, dass

$b(t)=2\cdot \sqrt{100-\sqrt{10.000-\dfrac{h(t)}{0,0006}}}$

ein Funktionsterm dieser Funktion $b$ ist.

(4P)

a) $\blacktriangleright$ Bestimme die mittlere Änderungsrate

Die Pegelhöhe wird durch die Funktion $h$ beschrieben. Die Änderungsrate $R$ in einem Intervall $[a;b]$ einer Funktion $h$ wird durch die Steigung zwischen den Punkten an den Stellen $a$ und $b$ in diesem Intervall bestimmt. Die Steigung ist die Differenz der Funktionswerte geteilt durch die Länge des Intervalls:

$\begin{array}[t]{rll} R&=&\dfrac{h(b)-h(a)}{b-a}\\[5pt] &=&\dfrac{h(3)-h(0)}{3-0}\\[5pt] &=&\dfrac{\dfrac{3}{2}\cdot \mathrm e^{-\dfrac{1}{18}(3-8)^2}+4-\left(\dfrac{3}{2}\cdot \mathrm e^{-\dfrac{1}{18}(0-8)^2}+4\right)}{3}\\[5pt] &\approx&\dfrac{\dfrac{3}{2}\cdot 0,25-\dfrac{3}{2}\cdot0,03}{3}\\[5pt] &=&\dfrac{0,33}{3}\\[5pt] &=&0,11\\[5pt] \end{array}$

Die mittlere Änderungsrate im Intervall $[0\,;\,3]$ beträgt in etwa $0,11\,$ Meter pro Tag.

$\blacktriangleright$ Zweite Ableitung herleiten

Die erste Ableitung bildet sich aus der Funktion $h$ . Du kannst erkennen, dass die erste Ableitung sich mit der Kettenregel bilden lässt.

$\begin{array}[t]{rll} h(t)&=& \dfrac{3}{2}\cdot \mathrm e^{-\frac{1}{18}(t-8)^2}+4\\[5pt] h(u(t))&=& \dfrac{3}{2}\cdot \mathrm e^{u(t)}+4\\[5pt] u(t)&=&-\dfrac{1}{18}(t-8)^2\\[5pt] \end{array}$

$\mathrm e^u$ nach $u$ abgeleitet ist $e^u$ . Das bedeutet, dass bei jeder weiteren Ableitung dieser Teil der Funktion stehen bleiben wird. Um die zweite Ableitung zu bilden, musst du jetzt zusätzlich die Produktregel beachten.

$\begin{array}[t]{rll} h‘(t)&=&-\dfrac{1}{6}\cdot(t-8)\cdot \mathrm e^{-\frac{1}{18}(t-8)^2}\\[5pt] &=&v(t)\cdot \mathrm e^{u(t)}\\[5pt] v(t)&=&-\dfrac{1}{6}\cdot(t-8)\\[5pt] h‘‘(t)&=&v(t)\cdot u‘(t) \cdot \mathrm e^{u(t)}+ v‘(t) \cdot e^{u(t)}\\[5pt] &=&-\dfrac{1}{6}\cdot(t-8)\cdot\left(-\dfrac{2}{18}\right)\cdot(t-8)\cdot \mathrm e^{u(t)} - \dfrac{1}{6} \cdot \mathrm e^{u(t)}\\[5pt] &=&\left(\dfrac{1}{54}(t-8)^2-\dfrac{1}{6}\right)\cdot \mathrm e^{u(t)}\\[5pt] &=&\left(\dfrac{1}{54}(t-8)^2-\dfrac{1}{6}\right)\cdot \mathrm e^{-\dfrac{1}{18}(t-8)^2}\\[5pt] \end{array}$

$\blacktriangleright$ Berechne globale Extrema

Gesucht sind die globalen Extrema im Intervall $[0\,;\,14]$ . Suche also lokale Extrema mit den Bedingungen:

Notwendige Bedingung: $h‘(x)=0$

Hinreichende Bedingung: $h‘‘(x)\neq0$

Für Maxima muss $h‘‘(x)<0$ , für Minima $h‘‘(x)>0$ . Zusätzlich musst du Randextrema untersuchen.

1. Schritt: Notwendige Bedingung überprüfen

$\begin{array}[t]{rll} h‘(t)&=& 0 \\[5pt] -\dfrac{1}{6}\cdot(t-8)\cdot\mathrm e^{-\frac{1}{18}(t-8)^2}&=&0 &\quad&\scriptsize\mid\; :\left(-\dfrac{1}{6}\right)\\[5pt] (t-8)\cdot \mathrm e^{-\frac{1}{18}(t-8)^2}&=&0\\[5pt] \end{array}$

Der Satz vom Nullprodukt besagt, dass wenn in einem Produkt mindestens ein Faktor Null ist, das Produkt Null wird. Die Exponentialfunktion wird nie Null, daher betrachtest du nur den anderen Teil des Terms.

$\begin{array}[t]{rll} (t-8)\cdot \mathrm e^{-\frac{1}{18}(t-8)^2}&=&0 &\quad&\scriptsize\mid\; :\left(\mathrm e^{-\frac{1}{18}(t-8)^2}\right)\\[5pt] t-8&=&0 &\quad&\scriptsize\mid\; +8 \\[5pt] t&=&8\\[5pt] \end{array}$

Bei $t=8$ ist ein lokale Extremstelle.

2. Schritt: Hinreichende Bedingung überprüfen

Der Funktionswert der zweiten Ableitung an der Stelle $t=8$ ist:

$\begin{array}[t]{rll} h‘‘(8)&=&\left(\dfrac{1}{54}(8-8)^2-\dfrac{1}{6}\right)\cdot \mathrm e^{-\dfrac{1}{18}(8-8)^2}\\[5pt] &=&-\dfrac{1}{6}<0\\[5pt] \end{array}$

An der Stelle $t=8$ liegt ein lokales Maximum vor.

3. Schritt: Maximum und Randextrema bestimmen

$\begin{array}[t]{rll} h(t=8)&=&\dfrac{3}{2}\cdot \mathrm e^{-\frac{1}{18}(8-8)^2}+4\\[5pt] &=&\dfrac{3}{2}\cdot 1 +4\\[5pt] &=&5,5\\[5pt] h(t=0)&=&\dfrac{3}{2}\cdot \mathrm e^{-\frac{1}{18}(0-8)^2}+4\\[5pt] &=&\dfrac{3}{2}\cdot \mathrm e^{-\frac{64}{18}}+4\\[5pt] &\approx&\dfrac{3}{2}\cdot 0,029 + 4\\[5pt] &\approx&4,04 \\[5pt] h(t=14)&=&\dfrac{3}{2}\cdot \mathrm e^{-\frac{1}{18}(14-8)^2}+4\\[5pt] &=&\dfrac{3}{2}\cdot \mathrm e^{-\frac{36}{18}}+4\\[5pt] &\approx&\dfrac{3}{2}\cdot 0,135 +4 \\[5pt] &\approx&4,2\\[5pt] \end{array}$

Die Pegelhöhe ist nach 8 Tagen maximal, der Pegelstand beträgt dann in etwa $5,5\,$ m. Die niedrigste Pegelhöhe ist zu Beginn der Beobachtung, also bei $t=0$ . Sie betrug in etwa $4,04\,$ m.

$\blacktriangleright$ Wendestellen berechnen

Die notwendige Bedingung für Wendestellen ist:

$\begin{array}[t]{rll} f‘‘(x_W)&=&0\\[5pt] \end{array}$

Eine hinreichende Bedingung musst du hier nicht überprüfen.

$\begin{array}[t]{rll} h‘‘(t)&=&0\\[5pt] \left(\dfrac{1}{54}(t-8)^2-\dfrac{1}{6}\right)\cdot \mathrm e^{-\frac{1}{18}(t-8)^2}&=&0 &\quad&\scriptsize\mid\; :\mathrm e^{-\frac{1}{18}(t-8)^2} \\[5pt] \dfrac{1}{54}(t-8)^2-\dfrac{1}{6} &=& 0 \\[5pt] \dfrac{1}{54}\cdot t^2 -\dfrac{16}{54}\cdot t +\dfrac{64}{54}-\dfrac{1}{6} &=& 0 &\quad&\scriptsize\mid\; \cdot 54\\[5pt] t^2 -16t +55 &=& 0 \\[5pt] \end{array}$

Für diese Gleichung findest du mit der $pq$ -Formel zwei Lösungen:

$\begin{array}[t]{rll} t^2+p\cdot t +q &=&0 \\[5pt] t_{1/2}&=&-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}\\[5pt] t_{1/2}&=&8\pm\sqrt{64-55}\\[5pt] &=&8\pm 3\\[5pt] t_1&=& 11\\[5pt] t_2&=& 5\\[5pt] \end{array}$

Die Wendestellen sind $t_1=11$ und $t_2=5$ . An der Wendstelle $t_2$ ist die Änderungsrate des Pegelstandes am größten, das heißt der Pegel steigt schnellsten. An der Wendestelle $t_1$ ist die Änderungsrate des Pegelstandes am kleinsten, das heißt der Pegel sinkt am schnellsten.

$\blacktriangleright$ Graphen skizzieren

Zeichne den Graphen der Funktion $h$ . Nutze aus was du bereits bestimmt hast. Die Funktionswerte zu Beginn und am Ende der Beobachtung: $B(0\,|\,4,04)$ und $E(14\,|\,4,2)$ . Desweiteren kennst du die Wendestellen $t_1=11$ und $t_2=5$ . Und du kennst den Hochpunkt des Graphen: $H(8\,|\,5,5)$ . Der Graph sieht so aus:

b) $\blacktriangleright$ Integral berechnen

Hier sollst du den angegebenen Ausdruck mit deinem Taschenrechner berechnen:

$\begin{array}[t]{rll} A&=&\dfrac{1}{14}\displaystyle\int_{0}^{14}h(t)\;\mathrm dx\\[5pt] &=&\dfrac{1}{14}\displaystyle\int_{0}^{14}\dfrac{3}{2}\cdot\mathrm e^{-\dfrac{1}{18}(t-8)^2}+4\;\mathrm dx \\[5pt] &\approx& \dfrac{1}{14}\cdot 67\\[5pt] &\approx& 4,8\\[5pt] \end{array}$

Der Ausdruck ergibt $4,8$ . Der Ausdruck ist Formel für den Mittelwert der Funktion $h$ im Intervall $[0\,;\,14]$ . Das heißt der Ausdruck beschreibt die mittlere Pegelhöhe im Beobachtungszeitraum.

c) Kanalbett

Hier ist die Form eines achsensymmetrischen Kanalbetts durch eine Funktion $\boldsymbol{f}$ im Intervall $[-10\,;\,10]$ näherungsweise gegeben.

$\blacktriangleright$ Finde den Grad $\boldsymbol{k}$

Der Grad $k$ der Funktion $f$ muss gerade, also $k=2,4,6,...$ sein, damit der Graph der Funktion symmetrisch zur $y$ -Achse ist.

$\blacktriangleright$ Bestimme die Breite der Wasseroberfläche

Das Kanalbett wird durch die Funktion $f$ beschrieben. Der Funktionsterm von $f$ lautet:

$\begin{array}[t]{rll} f(x)&=&-0,0006\cdot x^4+0,12\cdot x^2\\[5pt] \end{array}$

Die normale Pegelhöhe beträgt $4\,$ m. Sie wird durch die Funktion $y=4$ beschrieben. Der Abstand der Schnittstellen der Funktion $f$ und $y=4$ beschreibt die Breite der Wasseroberfläche. Die Schnittstellen bestimmst du, indem du die beiden Funktionsterme gleichsetzt und nach $x$ auflöst:

$\begin{array}[t]{rll} f(x)&=&4\\[5pt] -0,0006\cdot x^4+0,12\cdot x^2&=&4 &\quad&\scriptsize\mid\; -4\\[5pt] -0,0006\cdot x^4+0,12\cdot x^2-4&=&0&\;& \text{sub: } x^2=u\\[5pt] -0,0006\cdot u^2+0,12 \cdot u -4 &=&0&\quad&\scriptsize\mid :(-0,0006)\\[5pt] u^2-200u+\dfrac{20.000}{3}&=&0\\[5pt] \end{array}$

Die Substitution ermöglicht es dir mit der $pq$ -Formel zwei Lösungen für $u$ zu erhalten. Mit einer Resubstituion erhältst du daraus die $x$ -Stellen.

$\begin{array}[t]{rll} u^2+pu+q&=&0\\[5pt] u_{1/2}&=& -\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}\\[5pt] u_{1/2}&=&100\pm\sqrt{10.000-\dfrac{20.000}{3}}\\[5pt] &\approx&100\pm 57,7\\[5pt] u_1&\approx& 42,3\\[5pt] u_2&\approx& 157,7\\[5pt] && &\scriptsize\mid\; \text{resub}:x=\pm\sqrt{u}\\[5pt] x_{1/2}&\approx&\pm\sqrt{42,3}\\[5pt] &\approx&\pm 6,5\\[5pt] x_{3/4}&\approx&\pm\sqrt{157,7}\\[5pt] &\approx&\pm12,6\\[5pt] \end{array}$

Die Schnittstellen $x_{3/4}\approx\pm12,6$ liegen außerhalb des gültigen Intervalls $[-10\,;\,10]$ und spielen deshalb keine Rolle. Der Abstand der Schnittstellen $x_1\approx 6,5$ und $x_2 \approx -6,5$ beträgt in etwa $13\,$ m. Bei einer Pegelhöhe von $4\,$ m ist die Breite der Wasseroberfläche in etwa $13\,$ m.

$\blacktriangleright$ Ermittel die Vergrößerung des Flächeninhalts

Hier sollst du bestimmen, um wie viel Prozent sich der Flächeninhalt der Querschnittsfläche vergrößert wenn die Pegelhöhe auf $5,5\,$ m zugenommen hat. Die prozentuale Erhöhung des Flächeninhalts berechnet sich wie folgt:

$p\%=100\%\cdot \left(\dfrac{A_2}{A_1}-1\right)$

Wobei $A_1$ den Flächeninhalt bei normalem Pegelstand beschreibt und $A_2$ den Flächeninhalt bei erhöhtem Pegel beschreibt. Der Flächeninhalt $A_1$ ist gegeben.

$\begin{array}[t]{rll} A_1&=&32,81\\[5pt] \end{array}$

Um den Flächeninhalt $A_2$ zu bestimmen, musst du den Flächeninhalt der in der Skizze grün markierten Flächen bestimmen. Es ist die Fläche zwischen dem Graphen der Funktion $f$ und der Funktion $y=5,5$ .

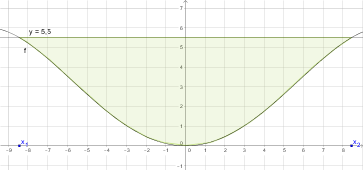Graf einer parabolischen Funktion in grün auf einem Koordinatensystem.

Der Flächeninhalt zwischen den Graphen der Funktionen ist:

$\begin{array}[t]{rll} A_2=\displaystyle\int_{x_1}^{x_2}f(x)-5,5\;\mathrm dx\\[5pt] \end{array}$

Wobei $x_1$ und $x_2$ die Schnittstellen der Funktionen sind. Sie sind durch die Hälfte der Wasserbreite gegeben:

$\begin{array}[t]{rll} x_1&=&-\dfrac{1}{2}\cdot 16,87\\[5pt] &=&-8,435\\[5pt] x_2&=&+8,435\\[5pt] \end{array}$

Der Flächeninhalt ist:

$\begin{array}[t]{rll} A_2&=&\displaystyle\int_{-8,435}^{8,435}-0,0006x^4+0,12x^2-5,5\;\mathrm dx\\[5pt] &\approx&55\\[5pt] \end{array}$

Die Vergrößerung kannst du jetzt berechnen:

$\begin{array}[t]{rll} p\%&=&100\%\cdot \left(\dfrac{A_2}{A_1}-1\right)\\[5pt] &=&100\%\cdot \left(\dfrac{55}{32,81}-1\right)\\[5pt] &\approx&67,6\%\\[5pt] \end{array}$

Der Flächeninhalt der Querschnittsfläche ist um etwa $67,6\%$ angestiegen.

d) Zeige, dass $\boldsymbol{b}$ die Breite beschreibt

Um zu zeigen, dass $b$ die Breite der Wasseroberfläche beschreibt, betrachtest du, wie du die Wasserbreite berechnet hast.

Die Wasserbreite ist der Abstand der Schnittstellen von der Funktion $f$ mit $y=h(x)$ . Die Schnittstellen hast du für $h=4$ bereits berechnet. Du kannst das nochmal für eine allgemeine Höhe berechnen:

$\begin{array}[t]{rll} f(x)&=&h(t)\\[5pt] -0,0006\cdot x^4+0,12\cdot x^2 &=&h(t) &\quad&\scriptsize\mid\; -h(t) \\[5pt] -0,0006\cdot x^4+0,12\cdot x^2 - h(t) &=& 0 &\quad&\scriptsize\mid\; :(-0,0006)\\[5pt] x^4 -200x^2+\dfrac{h(t)}{0,0006} &=& 0 &\;& \text{sub: }x^2=u\\[5pt] u^2 -200\cdot u + \dfrac{h(t)}{0,0006}&=& \\[5pt] \end{array}$

Mit der $pq$ -Formel erhältst du zwei Lösungen für $u$ .

$\begin{array}[t]{rll} u_{1/2}&=&-\dfrac{p}{2}\pm\sqrt{\left(\dfrac{p}{2}\right)^2-q}\\[5pt] &=&\dfrac{200}{2}\pm\sqrt{\left(\dfrac{200}{2}\right)^2-\dfrac{h(t)}{0,0006}}\\[5pt] &=&100\pm\sqrt{10.000-\dfrac{h(t)}{0,0006}}\\[5pt] \end{array}$

Aus der vorherigen Rechnung weißt du bereits, dass sich die "plus"-Lösung außerhalb des Definitionsbereichs befindet. Daher ist nur die "minus"-Lösung zu beachten. Durch eine Resubstitution erhältst du 2 Lösungen für $x$ . Die Breite ist gleich der Differenz der beiden Stellen.

$\begin{array}[t]{rll} u_1&=&100-\sqrt{10.000-\dfrac{h(t)}{0,0006}} \qquad \qquad \qquad \text{resub: }x=\pm\sqrt{u}\\[5pt] x_{1/2}&=&\pm\sqrt{100-\sqrt{10.000-\dfrac{h(t)}{0,0006}}}\\[5pt] b(t)&=&\left|x_1-x_2\right|\\[5pt] &=&+\sqrt{100-\sqrt{10.000-\dfrac{h(t)}{0,0006}}}-\left(-\sqrt{100-\sqrt{10.000-\dfrac{h(t)}{0,0006}}}\right)\\[5pt] &=&2\cdot \sqrt{100-\sqrt{10.000-\dfrac{h(t)}{0,0006}}}\\[5pt] \end{array}$

Wie du siehst, ist deine Funktion $b$ für die Breite gleich der gegebenen Funktion. Somit ist gezeigt, dass die Funktion $b$ die Breite der Wasseroberfläche beschreibt.