Hilfsmittelfreier Teil

HMF 1 - Analysis (Pool 1)

Gegeben ist die ganzrationale Funktion $f$ mit $f(x)=\frac{1}{3} x^{3}-3 x^{2}+8 x-\frac{8}{3}.$
Es ist $f^{\prime}(x)=x^{2}-6 x+8.$

1.1

Gib den Funktionswert von $f$ und die Steigung des Graphen von $f$ jeweils an der Stelle 2 an.

(2 P)

1.2

Untersuche, ob $3$ eine Wendestelle von $f$ ist.

(3 P)

HMF 2 - Analysis (Pool 1)

Betrachtet werden die in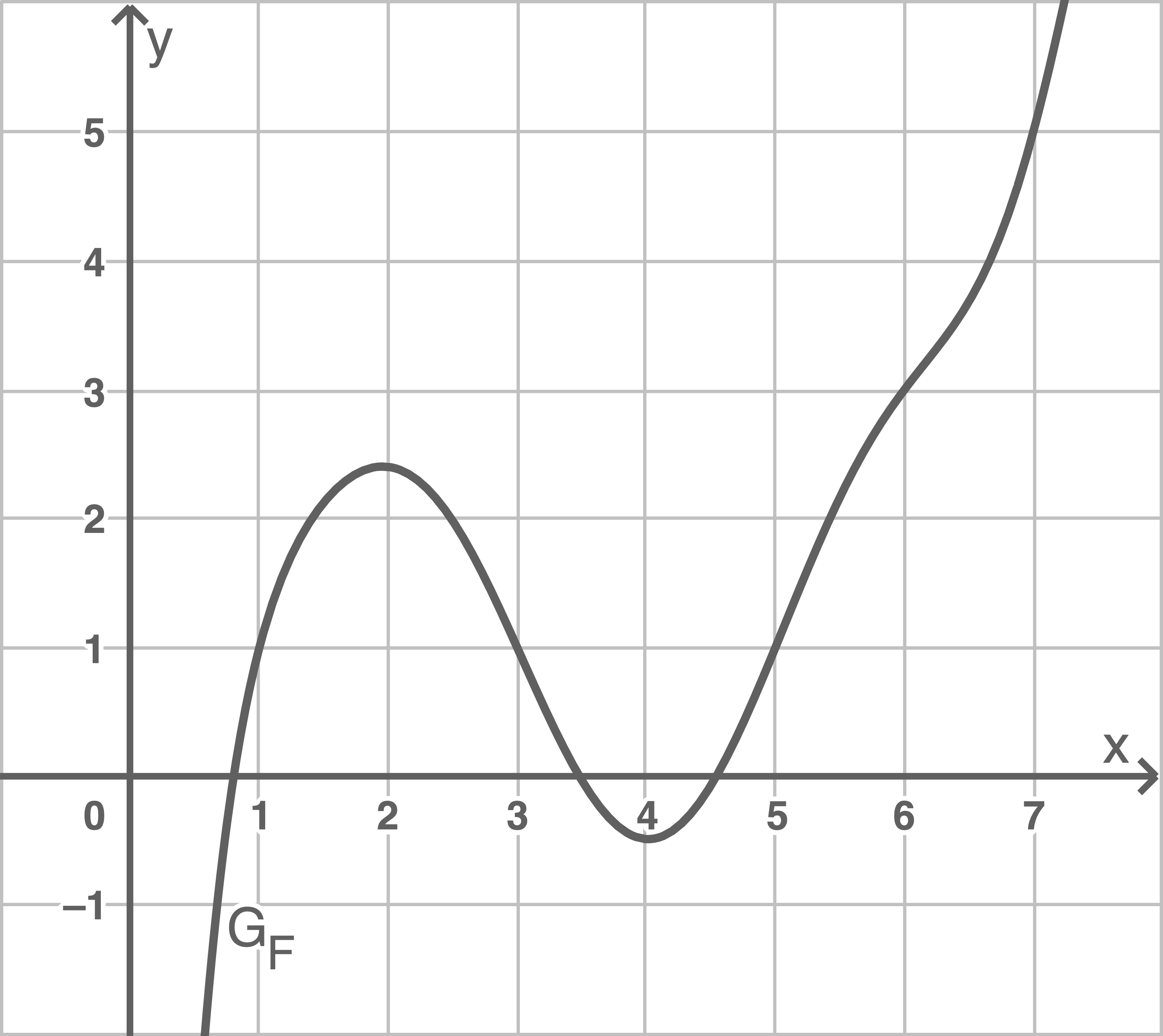 $\mathbb{R}$ definierten Funktionen $f$ und $F,$ wobei $F$ eine Stammfunktion von $f$ ist. Die Abbildung zeigt den Graphen $G_{F}$ von $F.$

funktionswert, tangente, abbildung, stammfunktion, ableitung

2.1

Bestimme den Wert des Integrals $\displaystyle\int_{1}^{7} f(x)\,\mathrm dx.$

(2 P)

2.2

Bestimme den Funktionswert von $f$ an der Stelle $1.$ Veranschauliche dein Vorgehen in der Abbildung.

(3 P)

HMF 3 - Analysis (Pool 2)

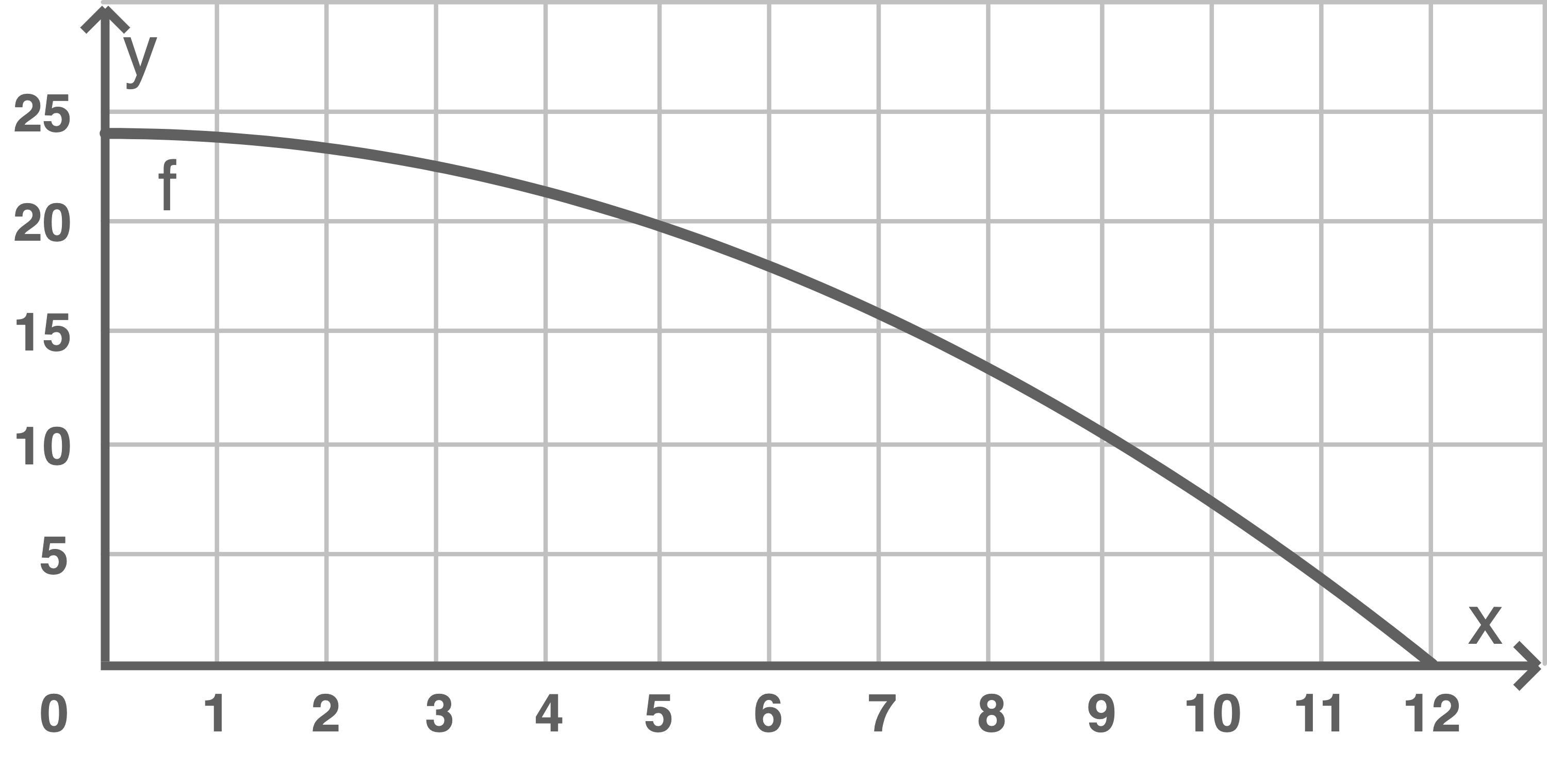
Im Koordinatensystem ist der Graph der Funktion $f$ mit $f(x) = 24-\frac{1}{6} x^{2}$ dargestellt.
Für jede Zahl $x$ mit $0 \lt x \lt 12$ wird ein Rechteck $R_{x}$ durch die Eckpunkte $(0 \mid 0),$ $(x \mid 0),$ $(x \mid f(x))$ und $(0 \mid f(x))$ festgelegt.

Funktionsgraph - Schleswig-Holstein Abi 2022 (Hilfsmittelfrei)

3.1

Zeichne das Rechteck $R_6$ in das Koordinatensystem.

(1 P)

3.2

Unter allen Rechtecken $R_{x}$ gibt es eines mit maximalem Flächeninhalt $A(x)=x \cdot f(x).$ Untersuche, ob für dieses Rechteck $x \lt 7$ ist.

(4 P)

HMF 4 - Analytische Geometrie (Pool 1)

Gegeben sind der Punkt $P(6 \mid 3 \mid 7)$ und die Ebene $E: 2 x_{1}+x_{2}+2 x_{3}=11.$

4.1

Gib eine Gleichung der Gerade $g$ an, die durch den Punkt $P$ und senkrecht zu $E$ verläuft.

(2 P)

Zusätzlich ist die Schar der Geraden $g_{a}: \vec{x}=\pmatrix{6 \\ 3 \\ 7}+t \cdot\pmatrix{2 \\ 1 \\ a}$ mit $t \in \mathbb{R}$ und $a \in \mathbb{R}$ gegeben.

4.2

Zeige, dass es genau einen Wert für $a$ gibt, so dass die zugehörige Gerade $g_{a}$ parallel zu $E$ ist und nicht in $E$ liegt.

(3 P)

HMF 5 - Analytische Geometrie (Pool 1)

Wird der Punkt $P(1\mid 2\mid 3)$ an der Ebene $E$ gespiegelt, so ergibt sich der Punkt $Q(7\mid 2\mid 11).$

5.1

Bestimme eine Gleichung von $E$ in Koordinatenform.

(3 P)

5.2

Auf der Gerade durch $P$ und $Q$ liegen die Punkte $R$ und $S$ symmetrisch bezüglich $E,$ dabei liegt $R$ bezüglich $E$ auf der gleichen Seite wie $P.$ Der Abstand von $R$ und $S$ ist doppelt so groB wie der Abstand von $P$ und $Q.$
Bestimme die Koordinaten von $R.$

(2 P)

HMF 6 - Stochastik (Pool 1)

In einem Unternehmen werden die Mitarbeitenden zu ihrem Arbeitsweg befragt. Zu den Ereignissen

$F:$ „Person kommt regelmäßig mit dem Fahrrad zur Arbeit “

$N:$ „Person wohnt nah an der Arbeitsstelle (in höchstens zehn Kilometern Entfernung)“

ergeben sich aus der Umfragestatistik die folgenden relativen Häufigkeiten:

	$N$	$\overline{N}$
$F$		$0,12$
$\overline{F}$			$0,70$
		$0,60$

6.1

Ergänze die fehlenden Werte in der Tabelle.

(2 P)

6.2

Von allen befragten Personen wird eine zufällig ausgewählt.
Berechne die Wahrscheinlichkeit $P_{\overline{N}}(F)$ und gib die Bedeutung dieser Wahrscheinlichkeit im Sachzusammenhang an.

(3 P)

HMF 7 - Stochastik (Pool 1)

Gegeben sind die im Folgenden beschriebenen Zufallsgrößen $X$ und $Y:$

Ein Würfel, dessen Seiten mit den Zahlen von 1 bis 6 durchnummeriert sind, wird zweimal geworfen. $X$ gibt die dabei erzielte Augensumme an.
Aus einem Behälter mit 60 schwarzen und 40 weißen Kugeln wird zwölfmal nacheinander jeweils eine Kugel zufällig entnommen und wieder zurückgelegt. $Y$ gibt die Anzahl der entnommenen schwarzen Kugeln an.

7.1

Begründe, dass die Wahrscheinlichkeit $P(X=4)$ mit der Wahrscheinlichkeit $P(X=10)$ übereinstimmt.

(2 P)

7.2

Die Wahrscheinlichkeitsverteilungen von $X$ und $Y$ werden jeweils durch eines der folgenden Diagramme I, II und III dargestellt.

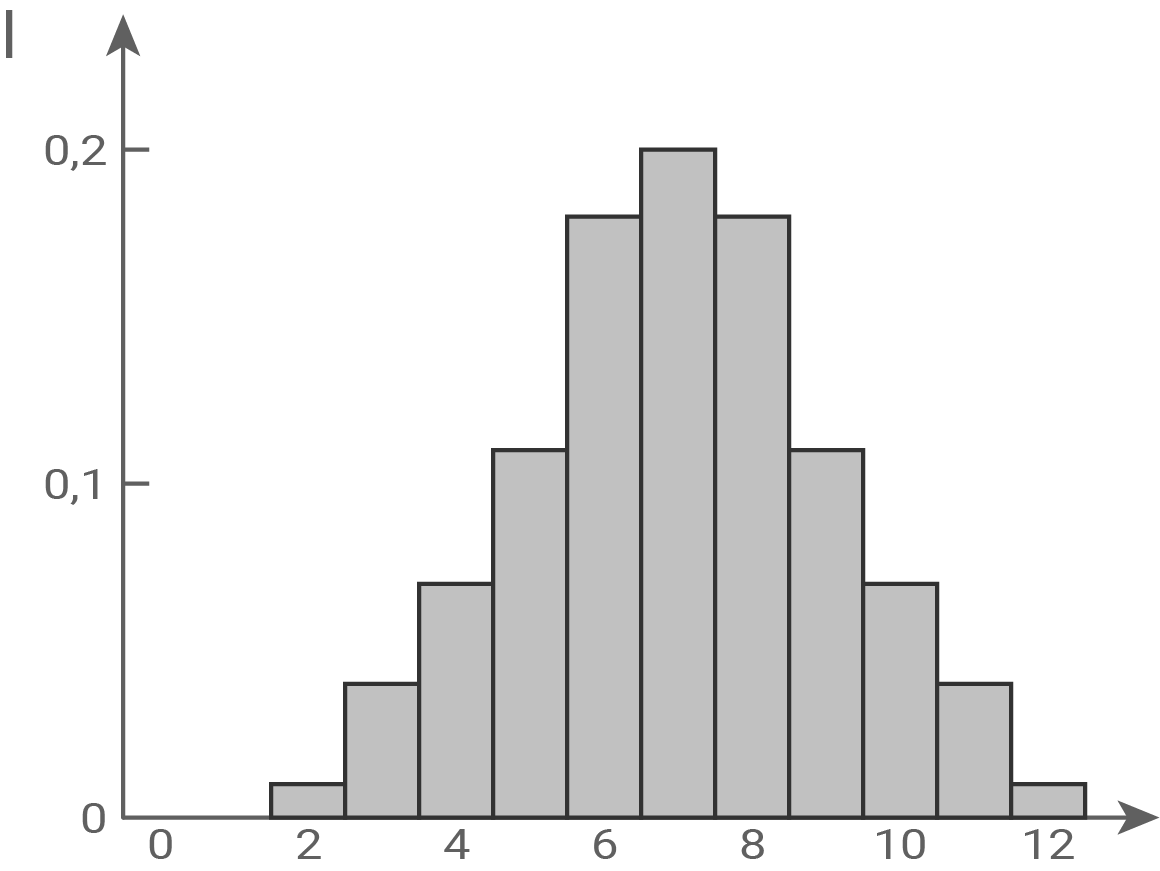
Mecklenburg-Vorpommern Abi 2022 Wahrscheinlichkeitsverteilungen 1

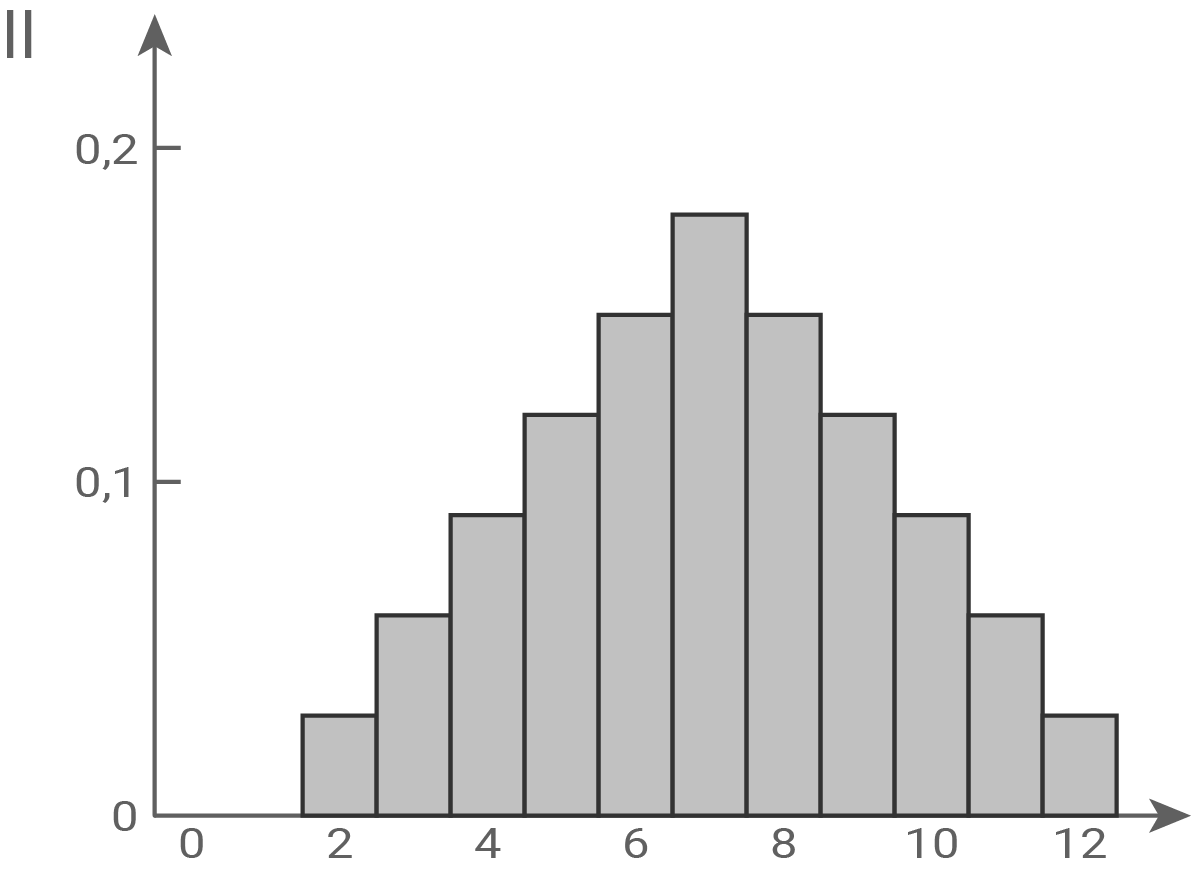
Mecklenburg-Vorpommern Abi 2022 Wahrscheinlichkeitsverteilungen 2

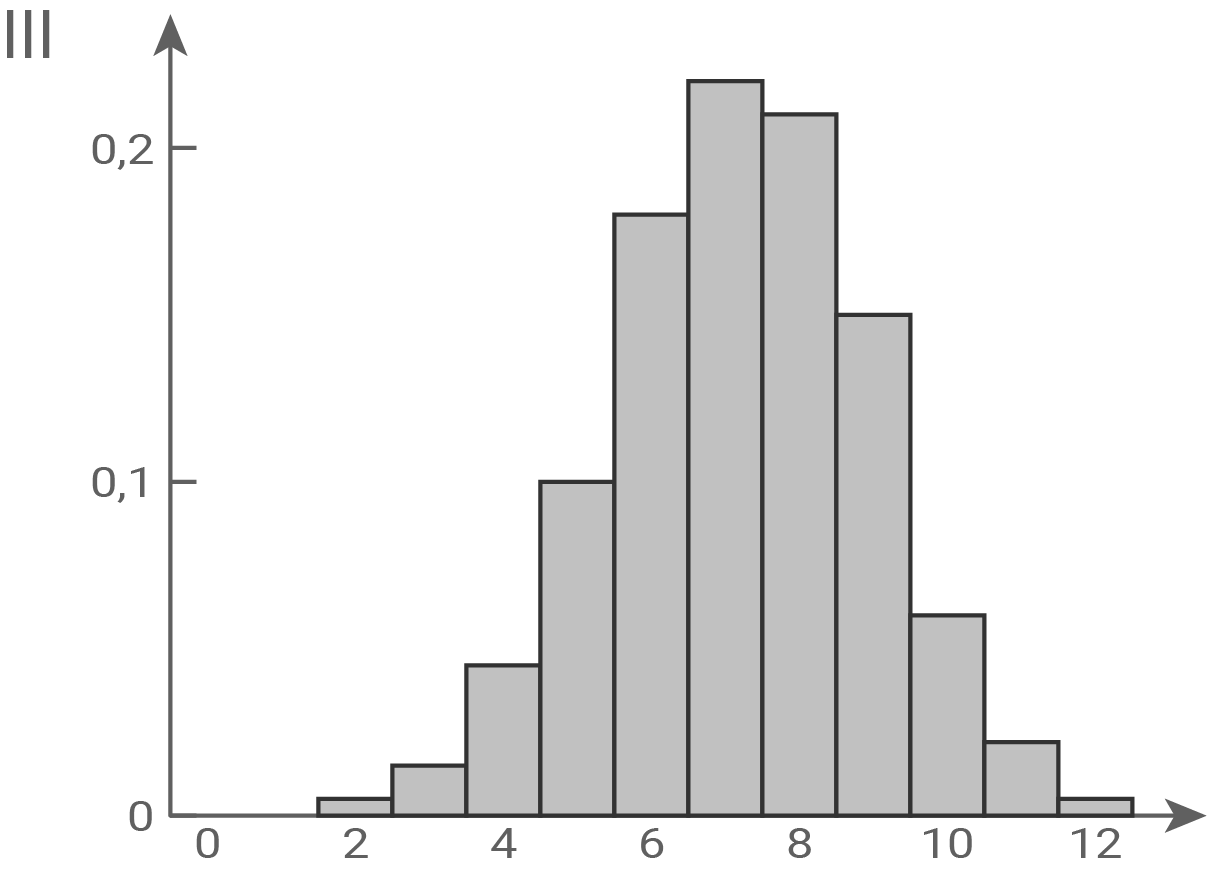Mecklenburg-Vorpommern Abi 2022 Wahrscheinlichkeitsverteilungen 3

Ordne $X$ und $Y$ jeweils dem passenden Diagramm zu und begründe deine Zuordnung.

(3 P)

HMF 8 - Stochastik (Pool 2)

Für ein Spiel wird ein Behälter mit $100$ Kugeln gefüllt. Dafür stehen rote und blaue Kugeln zur Verfügung. Vor jedem Spiel legt der Spieler die Anzahl der blauen Kugeln im Behälter fest. AnschlieBend wird dem Behälter eine Kugel zufällig entnommen. Ist diese Kugel rot, so wird dem Spieler die festgelegte Anzahl blauer Kugeln in Cent ausgezahlt; ist die Kugel blau, so beträgt die Auszahlung $10\,\text{Cent}.$

Ermittle, wie der Spieler die Anzahl blauer Kugeln für ein Spiel festlegen muss, damit der Erwartungswert der Auszahlung möglichst groß ist.

(5 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Lösung HMF 1 - Analysis (Pool 1)

1.1

$\(\begin{array}[t]{rll} f(2) &=& \frac{1}{3} \cdot 2^{3}-3 \cdot 2^{2}+8\cdot 2-\frac{8}{3} \\[5pt] &=& 4 \\[10pt] f$

An der Stelle $2$ beträgt der Funktionswert von $f$ $4$ und die Steigung des Graphen von $f$ Null.

1.2

Notwendiges Kriterium für Wendestellen $\(\boldsymbol{f$ überprüfen

$\(f$

Das notwendige Kriterium für Wendestellen ist an der Stelle $x=3$ also erfüllt.

Hinreichendes Kriterium für Wendestellen $\(\boldsymbol{f$ überprüfen

$\(f$

Das hinreichende Kriterium für Wendestellen ist also ebenfalls erfüllt, sodass $3$ eine Wendestelle von $f$ ist.

Lösung HMF 2 - Analysis (Pool 1)

2.1

$\displaystyle\int_{1}^{7}f(x)\;\mathrm dx = F(7) - F(1)$

Aus der Abbildung lassen sich $F(7)= 5$ und $F(1) = 1$ ablesen.

$\displaystyle\int_{1}^{7}f(x)\;\mathrm dx = F(7) - F(1) = 5-1 = 4$

2.2

$f$ ist die erste Ableitungsfunktion von $F.$ Der Funktionswert von $f$ an der Stelle $x=1$ beschreibt die Steigung des Graphen von $F$ bzw. die Steigung der Tangente an den Graphen von $F$ an der Stelle $x=1.$

Die Tangente lässt sich zusammen mit einem Steigungsdreieck in die Abbildung einzeichnen.

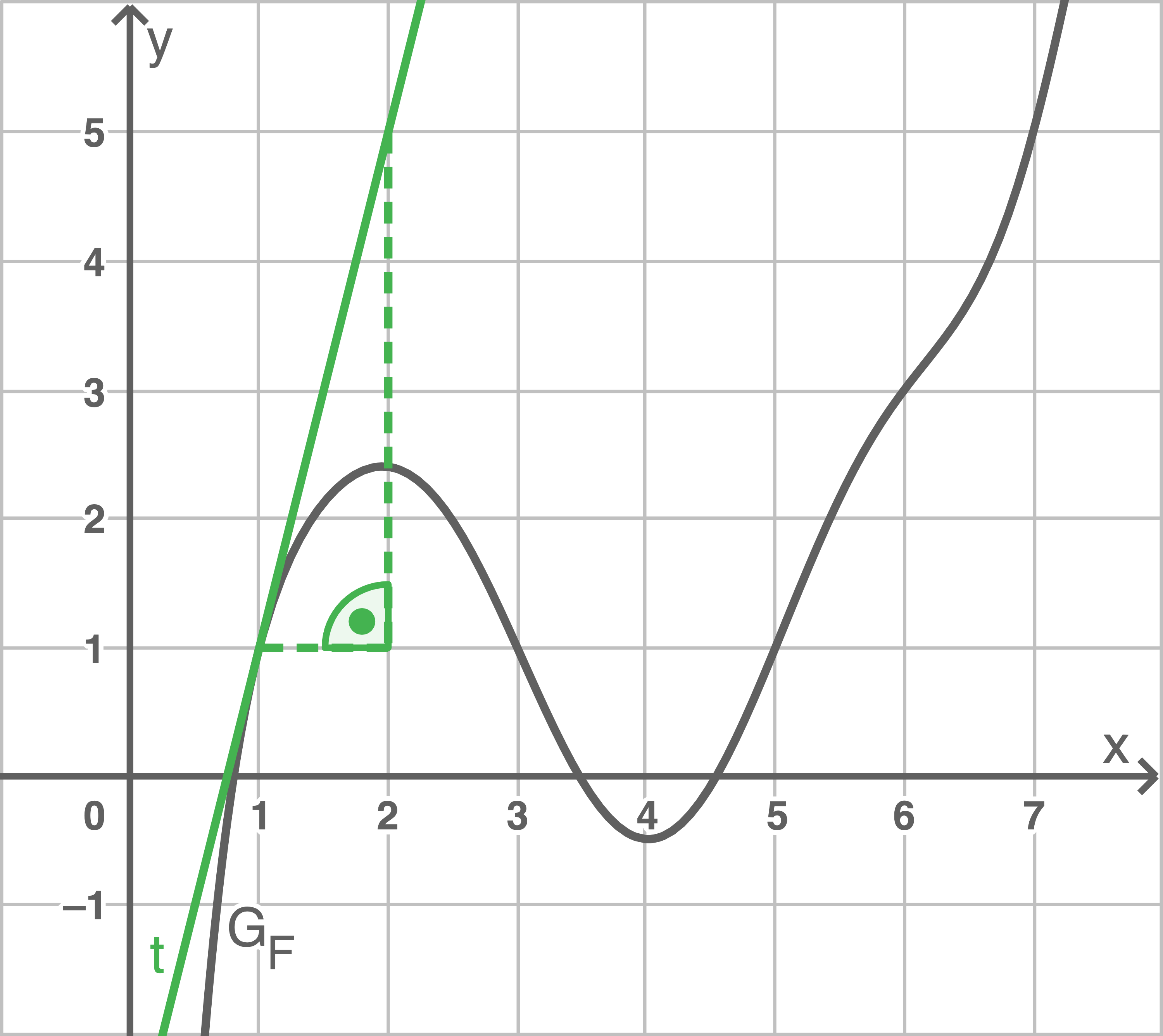
Steigungsdreieck Tangente - Schleswig-Holstein Abi 2022 (Hilfsmittelfrei)

$f(1) = \dfrac{5-1}{2-1} = 4$

Lösung HMF 3 - Analysis (Pool 2)

3.1

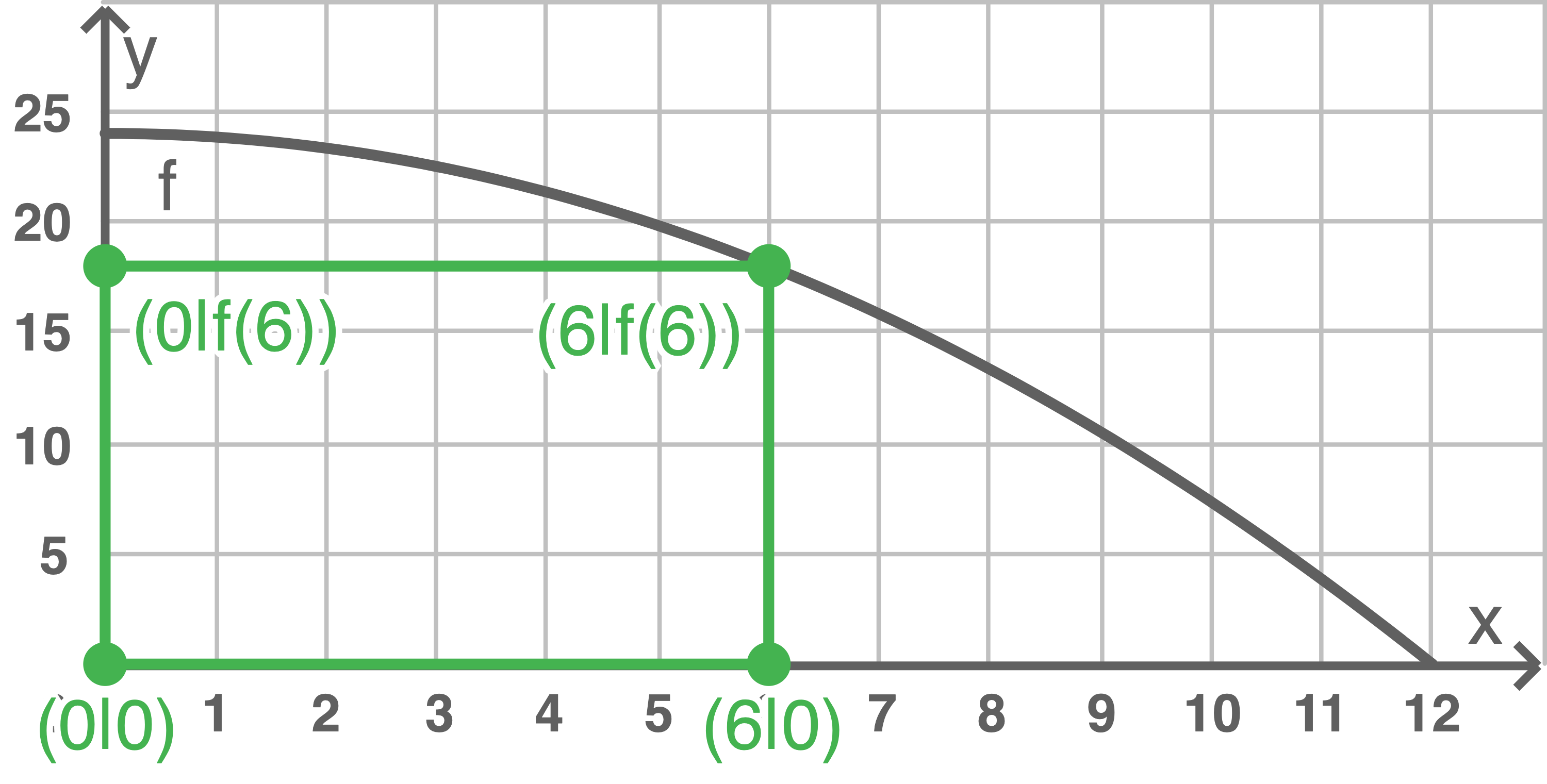
Rechteck - Schleswig-Holstein Abi 2022 (Hilfsmittelfrei)

3.2

Die Funktion $A$ muss zunächst auf Extrema untersucht werden.

1. Schritt: Ableitungsfunktionen bestimmen

$\(\begin{array}[t]{rll} A(x) &=& x\cdot f(x) \\[5pt] &=& x\cdot \left(24-\frac{1}{6}x^2\right)\\[5pt] &=& 24x-\frac{1}{6}x^3\\[10pt] A$

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\(\begin{array}[t]{rll} A$

$x_2 = -\sqrt{48}$ liegt außerhalb des betrachteten Bereichs.

3. Schritt: Hinreichendes Kriterium überprüfen

$\(A$

Bei $x= \sqrt{48} \lt \sqrt{49} = 7$ besitzt $A$ also eine Maximalstelle. Für das Rechteck $R_x$ mit dem maximalen Flächeninhalt gilt daher $x \lt 7.$

Lösung HMF 4 - Analytische Geometrie (Pool 1)

4.1

Ein Normalenvektor von $E$ verläuft senkrecht zu $E$ und kann aus der Ebenengleichung mit $\pmatrix{2\\1\\2}$ abgelesen werden. Dieser wird als Richtungsvektor von $g$ verwendet. Zusammen mit $\overrightarrow{OP}$ als Stützvektor folgt:

$g: \, \overrightarrow{x} = \pmatrix{6\\3\\7}+ s\cdot \pmatrix{2\\1\\2}$ mit $s\in \mathbb{R}.$

4.2

$g_a$ und $E$ verlaufen parallel zueinander, wenn der Richtungsvektor $\pmatrix{2\\1\\a}$ von $g_a$ und der Normalenvektor $\pmatrix{2\\1\\2}$ von $E$ senkrecht zueinander stehen. Dazu muss ihr Skalarprodukt Null ergeben:

$\begin{array}[t]{rll} \pmatrix{2\\1\\a} \circ \pmatrix{2\\1\\2} &=& 0 \\[5pt] 2\cdot 2 +1\cdot 1 +a\cdot 2 &=& 0 \\[5pt] 5 +2a &=& 0 &\quad \scriptsize \mid\; -5 \\[5pt] 2a&=& -5 &\quad \scriptsize \mid\; :2\\[5pt] a &=& -2,5 \end{array}$

Für $a= -2,5$ verläuft $g_a$ parallel zu $E.$ Es muss noch überprüft werden, ob $g_a$ in $E$ liegt.
Einsetzen der Koordinaten des Stützpunkts von $g_a$ in die Ebenengleichung:

$\begin{array}[t]{rll} 2x_1 +x_2 +2x_3 &=& 11 &\quad \scriptsize \mid\;(6\mid 3 \mid 7) \\[5pt] 2\cdot 6 + 3 +2\cdot 7 &=& 11 \\[5pt] 29 &=& 11 \end{array}$

Dies führt zu einem Widerspruch. Da der Stützpunkt von $g_a$ nicht in $E$ liegt, kann auch keine der Geraden $g_a$ in $E$ liegen. $a = -2,5$ ist zudem der einzige Wert von $a,$ für den $g_a$ und $E$ parallel sind.
Insgesamt gibt es also genau einen Wert von $a,$ für den $g_a$ und $E$ parallel sind, aber $g_a$ nicht in $E$ liegt.

Lösung HMF 5 - Analytische Geometrie (Pool 1)

5.1

Der Verbindungsvektor $\overrightarrow{PQ}= \pmatrix{6\\0\\8}$ verläuft senkrecht zu $E$ und kann daher als Normalenvektor verwendet werden.

Da $E$ die Strecke $\overline{PQ}$ mittig teilen muss, kann der Mittelpunkt $M$ dieser Strecke als Stützpunkt verwendet werden.

$\overrightarrow{OM} = \frac{1}{2}\cdot \left(\overrightarrow{OP}+\overrightarrow{OQ}\right)$ $= \frac{1}{2}\cdot \left(\pmatrix{1\\2\\3} + \pmatrix{7\\2\\11} \right) = \pmatrix{4\\2\\7}$

Einsetzen des Normalenvektors und des Mittelpunkts $M(4\mid 2\mid 7)$ in die allgemeine Koordinatenform:

$\begin{array}[t]{rll} 6x_1 +8x_3 &=& d &\quad \scriptsize \mid\; M(4\mid 2\mid 7)\\[5pt] 6\cdot 4 + 8\cdot 7 &=& d \\[5pt] 80 &=& d \end{array}$

Eine Gleichung von $E$ in Koordinatenform lautet:

$E:\, 6x_1 +8x_3 = 80$

5.2

$\overrightarrow{OR}=\overrightarrow{OM}-\overrightarrow{PQ}$ $= \pmatrix{4\\2\\7}-\pmatrix{6\\0\\8} =\pmatrix{-2 \\ 2 \\ -1}$

Die Koordinaten lauten $R(-2\mid 2\mid -1).$

Lösung HMF 6 - Stochastik (Pool 1)

6.1

Rechenweg anzeigen

	$N$	$\overline{N}$
$F$	$\color{#44B350}{0,18}$	$0,12$	$\color{#44B350}{0,30}$
$\overline{F}$	$\color{#44B350}{0,22}$	$\color{#44B350}{0,48}$	$0,70$
	$\color{#44B350}{0,40}$	$0,60$

6.2

$P_{\overline{N}}(F) = \dfrac{P(F\cap\overline{N})}{P(\overline{N})} = \dfrac{0,12}{0,60}$ $= \frac{12}{60} = \frac{1}{5} = 0,2=20\,\%$

Mit einer Wahrscheinlichkeit von $20\,\%$ kommt eine zufällig ausgewählte Person, die nicht nah an der Arbeitsstelle wohnt, regelmäßig mit dem Fahrrad zur Arbeit kommt.

Lösung HMF 7 - Stochastik (Pool 1)

7.1

Beiden Augensummen liegt die gleiche Anzahl an möglichen Ergebnissen mit jeweils der Wahrscheinlichkeit $\frac{1}{36}$ zu Grunde:

$X=4:$ $(1;3),(3;1),(2;2)$

$X=10:$ $(4;6),(6;4),(5;5)$

7.2

Die symmetrische Wahrscheinlichkeitsverteilung von $X$ wird durch Diagramm II dargestellt: Die Wahrscheinlichkeit $P(X=3)=\frac{2}{36}$ ist doppelt so groß wie $P(X=2)=\frac{1}{36}.$ Außerdem sind alle Wahrscheinlichkeiten von $X$ ganzzahlige Vielfache von $\frac{1}{36}$ . Das trifft nur auf Diagramm II zu.

$Y$ ist binomialverteilt mit $p=\frac{3}{5},$ die Wahrscheinlichkeitsverteilung von $Y$ ist nicht symmetrisch und wird durch Abbildung III dargestellt.

Lösung HMF 8 - Stochastik (Pool 2)

Bezeichnet man die festgelegte Anzahl blauer Kugeln mit $b,$ so kann der Erwartungswert der Auszahlung in Cent mit folgendem Term berechnet werden:

$\dfrac{100-b}{100} \cdot b+\frac{b}{100} \cdot 10$ $= \dfrac{(100-b)\cdot b +10b}{100}$ $= \dfrac{-b^2+110b}{100}$

Dieser lässt sich als Funktionsterm in Abhängigkeit von $b$ auffassen. Der zugehörige Graph entspricht einer nach unten geöffneten Parabel, die die $b$ -Achse bei $0$ und $110$ schneidet.
Der Scheitelpunkt und demnach höchste Punkt der Parabel befindet sich demnach bei $b = \frac{0+110}{2} = 55.$

Der Spieler muss sich also für $55$ blaue Kugeln entscheiden.

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

	$N$	$\overline{N}$
$F$	$0,30-0,12 = \color{#44B350}{0,18}$	$0,12$	$1-0,70 = \color{#44B350}{0,30}$
$\overline{F}$	$0,70-0,48 = \color{#44B350}{0,22}$	$0,60-0,12 = \color{#44B350}{0,48}$	$0,70$
	$1-0,60 = \color{#44B350}{0,40}$	$0,60$