Stochastik
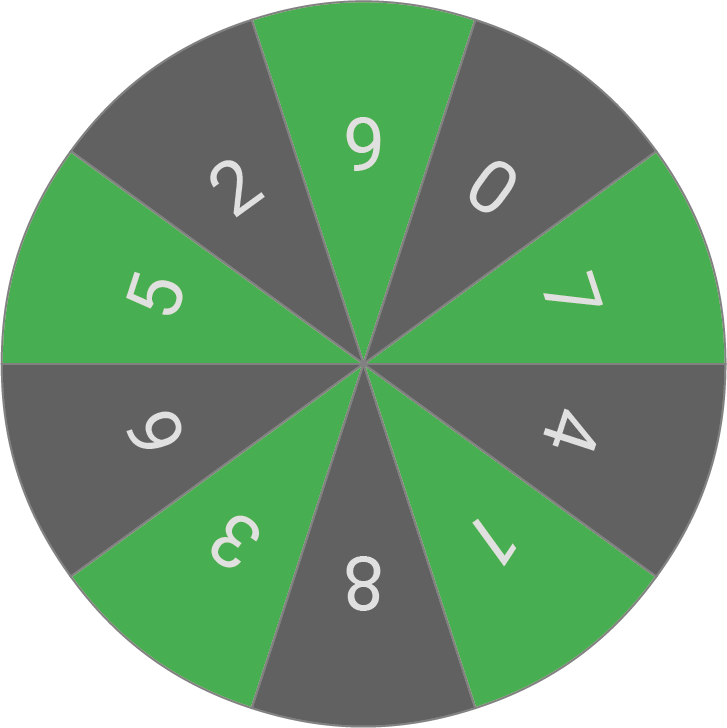
Die Sektoren des abgebildeten Glücksrads sind gleich groß und mit den Zahlen von 0 bis 9 durchnummeriert.
a)
a1)
Das Glücksrad wird zwanzigmal gedreht. Bestimmen Sie die Wahrscheinlichkeiten der folgenden Ereignisse 
und 
.
„Es wird genau siebenmal eine ungerade Zahl erzielt."
„Es wird weniger als neunmal eine ungerade Zahl erzielt."
„Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt.“
und .
„Es wird genau siebenmal eine ungerade Zahl erzielt."
„Es wird weniger als neunmal eine ungerade Zahl erzielt."
„Es wird mehr als siebenmal und höchstens zwölfmal eine ungerade Zahl erzielt.“
(5 P)
a2)
Das Glücksrad wird zweimal gedreht. Untersuche, ob die Ereignisse D und 
stochastisch unabhängig sind.
stochastisch unabhängig sind.
„Die Summe der erzielten Zahlen ist kleiner als 4.“
„Das Produkt der erzielten Zahlen ist 2 oder 3.“
(5 P)
b)
Mit dem Glücksrad wird ein Spiel durchgeführt. Jede spielende Person darf das Glücksrad beliebig oft drehen. Beendet sie das Spiel selbst, bevor sie eine „0“ erzielt, so wird ihr die Summe der erzielten Zahlen in Euro ausgezahlt. Erzielt sie eine „0“, so ist das Spiel dadurch beendet und es erfolgt keine Auszahlung.
b1)
Eine erste Spielerin entscheidet sich vor dem Spiel dafür, das Glücksrad, sofern sie keine „0" erzielt, viermal zu drehen und danach das Spiel zu beenden.
Bestimme die Wahrscheinlichkeit dafür, dass sie eine Auszahlung erhält.
Bestimme die Wahrscheinlichkeit dafür, dass sie eine Auszahlung erhält.
(2 P)
b2)
Bei einer zweiten Spielerin beträgt nach mehrmaligem Drehen des Glücksrads die Summe der erzielten Zahlen 
Die Spielerin entscheidet sich nun, das Glücksrad genau ein weiteres Mal zu drehen.
Berechne in dieser Situation den Erwartungswert für die Auszahlung.
Die Spielerin entscheidet sich nun, das Glücksrad genau ein weiteres Mal zu drehen.
Berechne in dieser Situation den Erwartungswert für die Auszahlung.
(3 P)
b3)
Wenn sich eine spielende Person vor dem Spiel dafür entscheidet, das Glücksrad, sofern sie keine „0“ erzielt, 
-mal zu drehen, dann kann der Erwartungswert für die Auszahlung mit dem Term 
berechnet werden.
Beurteile die folgende Aussage: „Es gibt zwei aufeinanderfolgende, aber nicht drei aufeinanderfolgende Werte von
für die die Erwartungswerte für die Auszahlung übereinstimmen.“
-mal zu drehen, dann kann der Erwartungswert für die Auszahlung mit dem Term berechnet werden.
Beurteile die folgende Aussage: „Es gibt zwei aufeinanderfolgende, aber nicht drei aufeinanderfolgende Werte von
für die die Erwartungswerte für die Auszahlung übereinstimmen.“
(4 P)
c)
Der Schüler Oskar legt einen zehnseitigen Spielwürfel mit den Ziffern 0 bis 9 auf den Tisch und behauptet, dass alle Zahlen des Würfels wie beim Glücksrad mit der gleichen Wahrscheinlichkeit auftreten. Die Schülerin Ronja würfelt mehrfach damit und vermutet, dass die Zahl 8 mit einer geringeren Wahrscheinlichkeit als von Oskar behauptet auftritt. Ronja plant einen Hypothesentest, um ihre Vermutung zu stützen.
c1)
Zunächst ermittelt Ronja die größte Anzahl 
mit der die Zahl 8 bei 240 Durchführungen auftreten darf, damit ihre Vermutung auf einem Signifikanzniveau von 
noch gestützt wird.
mit der die Zahl 8 bei 240 Durchführungen auftreten darf, damit ihre Vermutung auf einem Signifikanzniveau von noch gestützt wird.
- Gib die zugehörige Nullhypothese an und entscheide, ob ein rechtsseitiger oder linksseitiger Hypothesentest vorliegt.
- Ermittle die Anzahl
(6 P)
c2)
Schließlich hat Ronja, um ihre Vermutung zu stützen, einen einseitigen Hypothesentest mit einem Stichprobenumfang von 
und einem Signifikanzniveau von 
erstellt. Dabei hat sie den Verwerfungsbereich 
erhalten.
Bestimme alle ganzen Zahlen, die Ronja für
gewählt haben könnte, die zu dem ermittelten Verwerfungsbereich passen.
und einem Signifikanzniveau von erstellt. Dabei hat sie den Verwerfungsbereich erhalten.
Bestimme alle ganzen Zahlen, die Ronja für
gewählt haben könnte, die zu dem ermittelten Verwerfungsbereich passen.
(4 P)
d)
Ronja und Oskar haben ein Koordinatensystem gezeichnet und auf den Ursprung 
eine Spielfigur gestellt. Sie vereinbaren nun folgendes Spiel.
Das Glücksrad wird immer wieder gedreht. Tritt eine 7 , eine 8 oder eine 9 auf, so darf Oskar die Figur um zwei Einheiten nach oben (in 
-Richtung) bewegen.
Tritt eine der sieben anderen Zahlen auf, darf Ronja die Figur nur um eine Einheit nach rechts (in
-Richtung) verschieben.
Das Spiel endet mit einem Sieg für Ronja, wenn die Figur die-Koordinate 6 erreicht hat. Oskar gewinnt, wenn die Figur die -Koordinate 6 erreicht hat.
eine Spielfigur gestellt. Sie vereinbaren nun folgendes Spiel.
Das Glücksrad wird immer wieder gedreht. Tritt eine 7 , eine 8 oder eine 9 auf, so darf Oskar die Figur um zwei Einheiten nach oben (in -Richtung) bewegen.
Tritt eine der sieben anderen Zahlen auf, darf Ronja die Figur nur um eine Einheit nach rechts (in
-Richtung) verschieben.
Das Spiel endet mit einem Sieg für Ronja, wenn die Figur die
-Koordinate 6 erreicht hat. Oskar gewinnt, wenn die Figur die -Koordinate 6 erreicht hat.
d1)
Erläutere, warum die Figur bei diesem Spiel den Punkt 
nicht erreichen kann.
nicht erreichen kann.
(2 P)
d2)
Gib an, wie oft Ronja und wie oft Oskar die Figur seit Spielbeginn bewegt haben, falls die Figur auf dem Punkt 
steht.
Berechne, wie groß zu Spielbeginn die Wahrscheinlichkeit dafür ist, dass die Figur auf dem Punkt
zum Stehen kommt.
steht.
Berechne, wie groß zu Spielbeginn die Wahrscheinlichkeit dafür ist, dass die Figur auf dem Punkt
zum Stehen kommt.
(3 P)
d3)
Bestimme, wie groß zu Spielbeginn die Wahrscheinlichkeit dafür ist, dass Ronja gewinnt.
(6 P)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
a1)
Betrachtet wird die Zufallsgröße 
die die zufällige Anzahl der erzielten ungeraden Zahlen bei zwanzig Drehungen des Glücksrades beschreibt. 
kann als binomialverteilt mit 
und 
betrachtet werden.
![\(\begin{array}[t]{rll}
P(A)&=& P_{0,5}^{20}(X=7)\\[5pt]
&=& B(0,5;20;7) \\[5pt]
&\approx& 0,0739 \\[5pt]
&=& 7,39\,\% \\[10pt]
P(B) &=& P_{0,5}^{20}( X\lt 9) \\[5pt]
&=& P_{0,5}^{20}(X\leq 8) \\[5pt]
&=& F_{0,5}^{20}(8) \\[5pt]
&\approx& 0,2517 \\[5pt]
&=& 25,17\,\% \\[10pt]
P(C)&=& P_{0,5}^{20}(7\lt X\leq12) \\[5pt]
&=& P_{0,5}^{20}(X\leq12)-P_{0,5}^{20}(X\leq7) \\[5pt]
&=& F_{0,5}^{20}(12)-F_{0,5}^{20}(7) \\[5pt]
&\approx& 0,8684 - 0,1316 \\[5pt]
&=& 73,68\,\%
\end{array}\)](https://www.schullv.de/resources/formulas/ff75d4df345ba09d7a5a4a3f1448ece965e1d5814c4a31b1c9e9daeb6fe8e23c_light.svg)
die die zufällige Anzahl der erzielten ungeraden Zahlen bei zwanzig Drehungen des Glücksrades beschreibt. kann als binomialverteilt mit und betrachtet werden.
a2)
Die beiden Ereignisse 
und sind stochastisch unabhängig, wenn 
gilt.
Zu Ereignis gehören insgesamt die folgenden zehn Ergebnisse:
gehören insgesamt die folgenden vier Ergebnisse:
Mit der Pfadadditionsregel folgt:
Die Schnittmenge der beiden Ereignisse und sind 
und 
somit gilt:
Es folgt:
Somit sind die Ereignisse und nicht stochastisch unabhängig.
und sind stochastisch unabhängig, wenn gilt.
Zu Ereignis gehören insgesamt die folgenden zehn Ergebnisse:
gehören insgesamt die folgenden vier Ergebnisse:
Mit der Pfadadditionsregel folgt:
Die Schnittmenge der beiden Ereignisse und sind und somit gilt:
Es folgt:
Somit sind die Ereignisse und nicht stochastisch unabhängig.
b1)
Die Spielerin erhält eine Auszahlung, wenn in allen vier Drehungen keine Null erzielt wird.
Die Wahrscheinlichkeit, keine Null zu erzielen beträgt
Die Wahrscheinlichkeit dafür, dass die Spielerin eine Auszahlung erhält, beträgt somit:
Mit einer Wahrscheinlichkeit von 
erhält die Spielerin eine Auszahlung.
Die Wahrscheinlichkeit, keine Null zu erzielen beträgt
Die Wahrscheinlichkeit dafür, dass die Spielerin eine Auszahlung erhält, beträgt somit:
Mit einer Wahrscheinlichkeit von erhält die Spielerin eine Auszahlung.
b2)
Wert der Auszahlung in Euro
Jede Zahl hat die gleiche Wahrscheinlichkeit, erzielt zu werden. Somit folgt:
![\( = 58,5\,[€]\)](https://www.schullv.de/resources/formulas/55280f30589ef1ad429586b9effabc4feca0037b510cafde6c1eacff9f06f439_light.svg)
b3)
Damit für zwei aufeinanderfolgende Werte von der Erwartungswert übereinstimmt, muss ein mit 
existieren. Es folgt:
Der Erwartungswert für die Auszahlung ist somit für 
und 
Drehungen gleichgroß. Da die Gleichung nur eine Lösung besitzt, kann es zudem keine drei aufeinanderfolgenden Werte für geben, für die das gilt. Somit ist die Aussage aus der Aufgabenstellung korrekt.
der Erwartungswert übereinstimmt, muss ein mit existieren. Es folgt:
Der Erwartungswert für die Auszahlung ist somit für 
![\(\begin{array}[t]{rll}
5n\cdot0,9^n&=&5(n+1)\cdot0,9^{n+1} &\quad \scriptsize \mid\;:0,9^{n}\neq 0 \\[5pt]
5n &=& 5(n+1)\cdot 0,9 &\quad \scriptsize \mid\;:5 \\[5pt]
n &=& (n+1)\cdot 0,9 \\[5pt]
n &=& 0,9n+ 0,9 &\quad \scriptsize \mid\;-0,9n \\[5pt]
0,1n &=& 0,9 &\quad \scriptsize \mid\;\cdot 10 \\[5pt]
n&=& 9 \\[5pt]
\end{array}\)](https://www.schullv.de/resources/formulas/f1f7f5d45668c876386aa11196581771ceff480bdefdcfa679c0cf0f03b7bed7_light.svg)
und Drehungen gleichgroß. Da die Gleichung nur eine Lösung besitzt, kann es zudem keine drei aufeinanderfolgenden Werte für geben, für die das gilt. Somit ist die Aussage aus der Aufgabenstellung korrekt.
c1)
Art des Tests und Nullhypothese angeben
Ronja bestimmt die größte Anzahl damit ihre Vermutung gerade noch gestützt wird. Ist die Anzahl, mit der die Zahl 8 auftritt höher, so kann ihre Vermutung nicht gestützt werden. Es handelt sich daher um einen linksseitigen Hypothesentest mit der Nullhypothese:
Anzahl 
ermitteln
Betrachtet wird die Zufallsgröße die die zufällige Anzahl angibt, mit der die Zahl 8 bei 240 Durchführungen auftritt.
kann als binomialverteilt mit 
und im Extremfall der Nullhypothese 
angenommen werden.
Gesucht ist das größte sodass folgende Gleichung grade noch erfüllt ist:
Durch systematisches Ausprobieren ergibt sich mit dem Taschenrechner:
Das größte bei dem Ronjas Vermutung noch gestützt wird, ist also 
damit ihre Vermutung gerade noch gestützt wird. Ist die Anzahl, mit der die Zahl 8 auftritt höher, so kann ihre Vermutung nicht gestützt werden. Es handelt sich daher um einen linksseitigen Hypothesentest mit der Nullhypothese:
Anzahl ermitteln
Betrachtet wird die Zufallsgröße die die zufällige Anzahl angibt, mit der die Zahl 8 bei 240 Durchführungen auftritt.
kann als binomialverteilt mit und im Extremfall der Nullhypothese angenommen werden.
Gesucht ist das größte sodass folgende Gleichung grade noch erfüllt ist:
Durch systematisches Ausprobieren ergibt sich mit dem Taschenrechner:
Das größte bei dem Ronjas Vermutung noch gestützt wird, ist also
c2)
Betrachtet wird die Zufallsgröße die die zufällige Anzahl angibt, mit der die Zahl 8 bei 175 Durchführungen auftritt.
kann als binomialverteilt mit und im Extremfall der Nullhypothese angenommen werden.
Aufgrund des Verwerfungsbereichs 
sind ganze Zahlen gesucht, für die 
die größte Anzahl ist, sodass folgende Ungleichung erfüllt ist:
Es gilt:
Das Signifikanzniveau muss zwischen diesen beiden Werten liegen. Als ganze Zahlen kommen also 
und 
infrage.
die die zufällige Anzahl angibt, mit der die Zahl 8 bei 175 Durchführungen auftritt.
kann als binomialverteilt mit und im Extremfall der Nullhypothese angenommen werden.
Aufgrund des Verwerfungsbereichs sind ganze Zahlen gesucht, für die die größte Anzahl ist, sodass folgende Ungleichung erfüllt ist:
Es gilt:
Das Signifikanzniveau muss zwischen diesen beiden Werten liegen. Als ganze Zahlen kommen also und infrage.
d1)
Da die Figur immer nur entweder in -Richtung oder in -Richtung verschoben wird, kann sie nicht in einem Zug die - und -Koordinate 
erreichen, wenn sie nicht eines von beidem vorher schon hatte.
Erreicht die Figur allerdings die-Koordinate oder die -Koordinate 
dann ist das Spiel sofort beendet. Es findet also kein weiterer Zug mehr statt, mit dem die Figur auch in die andere Richtung bewegt werden könnte.
-Richtung oder in -Richtung verschoben wird, kann sie nicht in einem Zug die - und -Koordinate erreichen, wenn sie nicht eines von beidem vorher schon hatte.
Erreicht die Figur allerdings die
-Koordinate oder die -Koordinate dann ist das Spiel sofort beendet. Es findet also kein weiterer Zug mehr statt, mit dem die Figur auch in die andere Richtung bewegt werden könnte.
d2)
Wenn die Figur auf dem Punkt 
steht, hat Oskar die Figur seit Spielbeginn einmal bewegt und Ronja zweimal.
Gesucht ist also die Wahrscheinlichkeit dafür, dass bei drei Drehungen, genau einmal eine 
oder auftritt. Diese ergibt sich wie folgt:
Mit einer Wahrscheinlichkeit von 
kommt die Figur auf dem Punkt zum Stehen.
steht, hat Oskar die Figur seit Spielbeginn einmal bewegt und Ronja zweimal.
Gesucht ist also die Wahrscheinlichkeit dafür, dass bei drei Drehungen, genau einmal eine oder auftritt. Diese ergibt sich wie folgt:
Mit einer Wahrscheinlichkeit von kommt die Figur auf dem Punkt zum Stehen.
d3)
Damit Ronja gewinnt, muss sie die Figur sechsmal bewegen, während Oskar die Figur höchstens zweimal bewegen darf.
Wird mit die Anzahl der Drehungen beschrieben, bei denen Oskar die Figur bewegen darf, so gibt es drei Fälle, in denen Ronja gewinnt:
die Anzahl der Drehungen beschrieben, bei denen Oskar die Figur bewegen darf, so gibt es drei Fälle, in denen Ronja gewinnt:
- Oskar bewegt seine Figur gar nicht. Ronja gewinnt also, indem sechsmal hintereinander eine andere Zahl als oder getroffen wird:
- Oskar bewegt seine Figur einmal in sieben Drehungen, wobei er sie nicht in der letzten bewegt, da Ronja dann bereits bei der vorherigen Drehung gewonnen hätte:
- Oskar bewegt seine Figur zweimal in acht Drehungen, wobei er sie nicht in der letzten Drehung bewegt, da Ronja dann bereits bei der vorherigen Drehung gewonnen hätte:
