Analysis 1

Gegeben ist die Schar der in $\mathbb{R}$ definierten Funktionen $f_a$ mit $f_a(x)=x \cdot \mathrm{e}^{-\frac{1}{2}a\cdot x^{2}+\frac{1}{2}}$ und $a\in \mathbb{R}.$

Die zugehörigen Graphen sind symmetrisch bezüglich des Koordinatenursprungs.

Zunächst werden einzelne Funktionen der Schar betrachtet.

a1)

Berechne die Koordinaten des Hochpunkts des Graphen von $f_1.$

(4 P)

a2)

Weise nach, dass $f_1$ genau eine Nullstelle hat, und gib den Grenzwert von $f_1$ für $x\to +\infty$ an.

(2 P)

a3)

Die folgende Abbildung zeigt den Graphen von $f_1$ ohne das zugrunde liegende Koordinatensystem. Ergänze due Koordinatenachten und skaliere diese passend.

Funktionsgraph - Schleswig-Holstein Abi 2022 (Analysis)

(2 P)

a4)

Interpretiere den folgenden Sachverhalt geometrisch:

Für jede Stammfunktion $F_1$ von $f_1$ und für jede reelle Zahl $u \gt 2022$ gilt

$F_1(u)-F_1(0) \approx \displaystyle\int_{0}^{2022} f_1(x)\, \mathrm{d} x.$

(3 P)

a5)

Der Graph von $f_0$ ist eine Gerade. Gib die Steigung dieser Gerade und die Koordinaten ihres Schnittpunkts mit der $y$ -Achse an.

(2 P)

a6)

Für einen Wert von $a$ liegt der Punkt $P\left(1 \mid \mathrm e\right)$ auf dem Graphen von $f_{a}.$ Berechne für diesen Wert von $a$ die Größe des Winkels, den der Graph von $f_{a}$ mit der Parallele zur $x$ -Achse durch den Punkt $P$ einschließt.

(4 P)

a7)

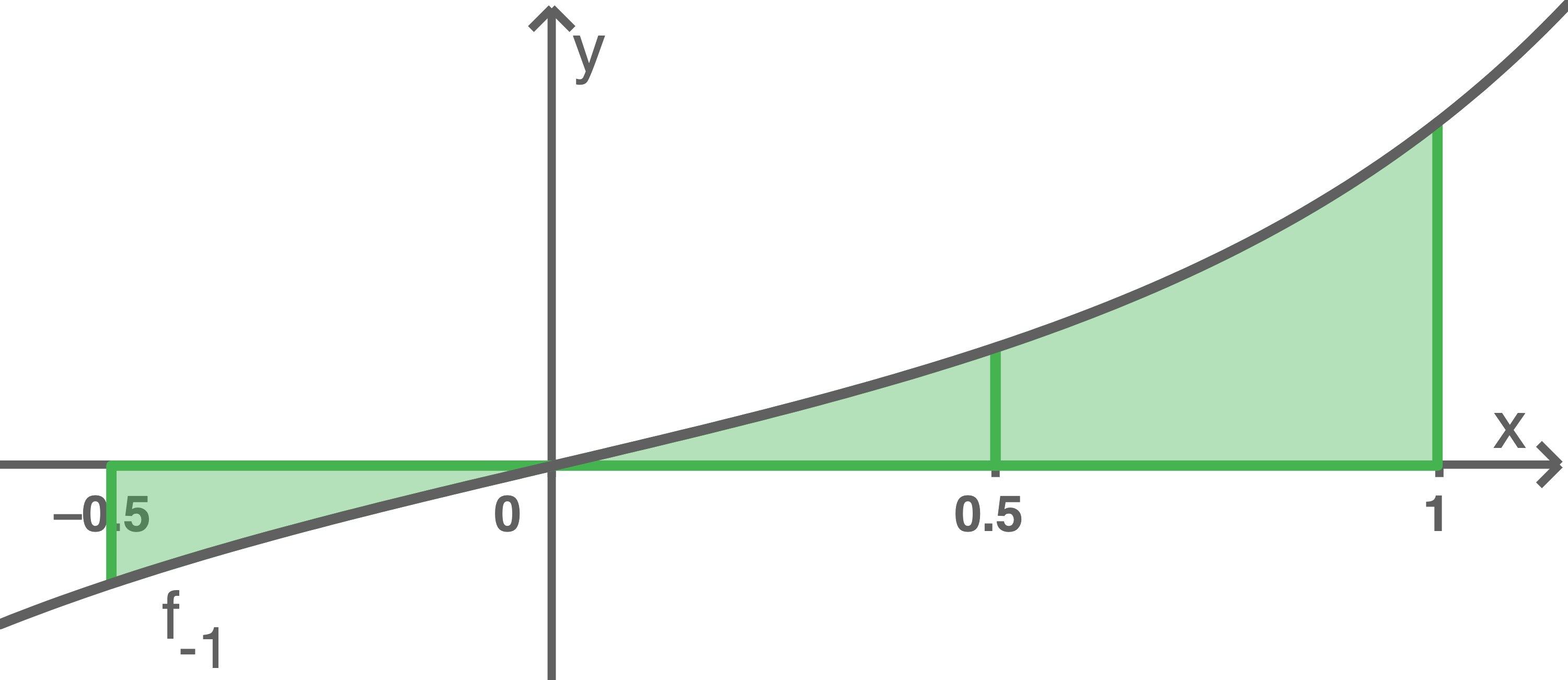
Begründe unter Verwendung der folgenden Abbildung, dass

$\displaystyle\int_{-0,5}^{1} f_{-1}(x) \mathrm{d} x=\displaystyle\int_{0,5}^{1} f_{-1}(x) \mathrm{d} x$

gilt.

Fläche - Schleswig-Holstein Abi CAS 2022 (Analysis 1)

(2 P)

Nun werden alle Funktionen der gegebenen Schar betrachtet.

b1)

Die folgenden Aussagen gelten für alle reellen Zahlen $a, a_{1}$ und $a_{2}:$

$f_{a}(0)=0$

$f_{a}^{\prime}(0)=f_{0}^{\prime}(0)$

$f_{a_{1}}(x)=f_{a_{2}}(x) \Leftrightarrow a_{1}=a_{2} \vee x=0$

Gib an, was sich aus diesen Aussagen hinsichtlich des Verlaufs der Graphen der Schar folgern lässt.

(3 P)

b2)

Zeige, dass die folgende Aussage für jeden Wert von $a$ richtig ist:

Wird der Graph von $f_{a}$ mit dem gleichen Faktor $k\gt 0$ sowohl in $x$ -Richtung als auch in $y$ -Richtung gestreckt, so stellt der dadurch entstehende Graph ebenfalls eine Funktion der Schar dar.

(3 P)

b3)

Für jedes $a \in \mathbb{R}\setminus\{0\}$ sind die Wendestellen von $f_{a}$ genau die Lösungen der Gleichung $\left(a \cdot x^{2}-3\right) \cdot x=0.$
Gib für alle Werte von $a \in \mathbb{R}$ die Anzahl der Wendestellen von $f_{a}$ an und begründe deine Angabe.

(5 P)

c1)

Zeige, dass alle Extrempunkte der Graphen der Schar auf der Gerade mit der Gleichung $y=x$ liegen.

(5 P)

c2)

Für jeden positiven Wert von $a$ bilden der Hochpunkt $\left(v \mid f_{a}(v)\right)$ des Graphen von $f_{a},$ der Punkt $\left(0 \mid 2\right),$ der Koordinatenursprung und der Punkt $(v \mid 0)$ die Eckpunkte eines Vierecks.

Bestimme ausgehend von einer geeigneten Skizze denjenigen Wert von $a,$ für den das Viereck den Flächeninhalt $144$ hat.

(5 P)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

a1)

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

Für eine lokale Extremstelle $x_E$ von $f_1$ muss $\(f_1$ gelten.

$f_1(x)= x\cdot \mathrm e^{-\frac{1}{2}x^2+\frac{1}{2}}$

Mit der Produktregel folgt:

$\(f_1$ $=(1-x^2)\cdot \mathrm e^{-\frac{1}{2}x^2+\frac{1}{2}}$

Mit dem Satz vom Nullprodukt gilt, dass $\(f_1$ für $1-x^2$ oder $\mathrm e^{-\frac{1}{2}x^2+\frac{1}{2}}=0$ erfüllt ist. Allerdings gilt $\mathrm e^{-\frac{1}{2}x^2+\frac{1}{2}} \neq 0$ für alle $x\in \mathbb{R}.$ Also folgt:

$\begin{array}[t]{rll} 1-x^2 &=& 0 &\quad \scriptsize \mid\; +x^2 \\[5pt] 1 &=& x^2 \\[5pt] \pm 1 &=& x \\[5pt] x_{1/2} &=& \pm 1 \\[5pt] \end{array}$

2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen

Mit der Produktregel folgt:

Rechenweg anzeigen

$\( f_1$

Einsetzen von $x_1$ und $x_2:$

$\(f_1$ $= 2 \gt 0$

$\(f_1$ $=-2 \lt 0$

3. Schritt: $\boldsymbol{y}$ -Koordinate berechnen

$f_1(1) = 1\cdot \mathrm e^{-\frac{1}{2}\cdot 1^2+\frac{1}{2}} = 1$

Der Hochpunkt des Graphen von $f_1$ hat die Koordinaten $H(1\mid 1).$

a2)

Nullstelle nachweisen

$f_1(x)= 0$ ist erfüllt, wenn $x\cdot \mathrm e^{-\frac{1}{2}\cdot x^2+\frac{1}{2}} =0$ gilt.

Wegen dem Satz vom Nullprodukt und $\mathrm e^{-\frac{1}{2}\cdot x^2+\frac{1}{2}} \neq 0$ für alle $x\in \mathbb{R}$ ist das genau dann der Fall, wenn $x=0$ gilt.

Somit ist $x=0$ die einzige Nullstelle von $f_1.$

Grenzwert angeben

$\displaystyle\lim _{x \rightarrow+\infty} f_{1}(x)= \displaystyle\lim _{x \rightarrow+\infty}x\cdot \mathrm e^{-\frac{1}{2}x^2+\frac{1}{2}} =0$

a3)

Mit Hilfe des Grenzwerts aus a2) lässt sich die $x$ -Achse als Asymptote einzeichnen.
Mit den Koordinaten des Hochpunkts $H(1\mid 1)$ aus a1) lässt sich die $y$ -Achse sowie die Skalierung der Achsen eintragen.

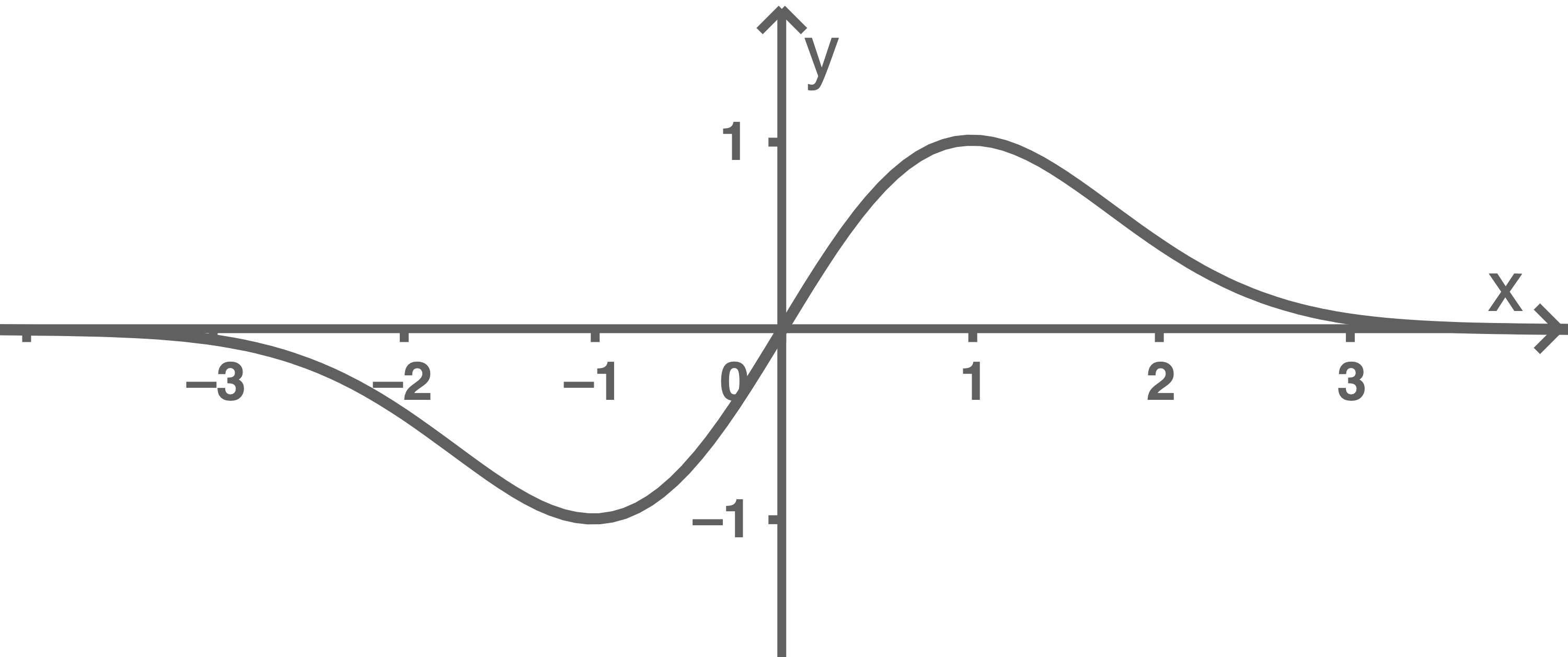
Koordinatenachten - Schleswig-Holstein Abi 2022 (Analysis 1)

a4)

Für jede reelle Zahl $u \gt 2022$ stimmt der Inhalt des Flächenstückes zwischen dem Graphen von $f_1$ und der $x$ -Achse über dem Intervall $[0 ; u]$ ungefähr mit dem Inhalt des Flächenstückes überein, das zwischen dem Graphen von $f_1$ und der $x$ -Achse über dem Intervall $[0 ; 2022]$ liegt.

a5)

$f_0(x) = x\cdot \mathrm e^{-\frac{1}{2} \cdot 0 \cdot x^{2}+\frac{1}{2}} = x\cdot \mathrm e^{\frac{1}{2}}.$

Die Steigung der Gerade ist $\mathrm e^{\frac{1}{2}}.$ Die Gerade schneidet die $y$ -Achse im Punkt $(0\mid 0).$

a6)

1. Schritt: Wert für $\boldsymbol{a}$ berechnen

$\begin{array}[t]{rll} f_a(1) &=& \mathrm e \\[5pt] 1\cdot \mathrm e^{-\frac{1}{2} \cdot a \cdot 1^{2}+\frac{1}{2}} &=& \mathrm e \\[5pt] \mathrm e^{-\frac{1}{2} \cdot a +\frac{1}{2}} &=& \mathrm e &\quad \scriptsize \mid\;\ln \\[5pt] -\frac{1}{2} \cdot a +\frac{1}{2} &=& 1 &\quad \scriptsize \mid\;-\frac{1}{2} \\[5pt] -\frac{1}{2} \cdot a &=& \frac{1}{2} &\quad \scriptsize \mid\;\cdot (-2) \\[5pt] a &=& -1 \end{array}$

Der gesuchte Winkel $\varphi$ ist der Steigungswinkel des Graphen von $f_{-1}$ an der Stelle $x=1.$ Mit der zugehörigen Formel und der Ableitungsfunktion des CAS ergibt sich:

$\(\begin{array}[t]{rll} \tan (\varphi) &=& f_{-1}$

a7)

Da die beiden Flächenstücke zwischen dem Graph von $f_{-1}$ und der $x$ -Achse über dem Intervall $[-0,5 ; 0]$ bzw. $[0 ; 0,5]$ gleich groß und unterschiedlich orientiert sind, ist $\displaystyle\int_{-0,5}^{0,5} f_{-1}(x)\; \mathrm{d} x =0$

b1)

Alle Graphen der Schar verlaufen durch den Koordinatenursprung.
An der Stelle $x=0$ besitzen alle Graphen der Schar dieselbe Steigung.
Je zwei verschiedene Graphen der Schar schneiden sich nur an der Stelle $x=0.$

b2)

Wird der Graph der Funktion $f_{a}$ mit dem Faktor $k\gt 0$ in $x$ - und $y$ -Richtung gestreckt, ergibt sich der zugehörige Funktionsterm durch:

$k \cdot f_{a}\left(\frac{1}{k} \cdot x\right)=k\cdot \frac{1}{k}\cdot x \cdot \mathrm{e}^{-\frac{1}{2}\cdot a \cdot \left(\frac{1}{k}\cdot x\right)^{2}+\frac{1}{2}}$ $=x \cdot \mathrm{e}^{-\frac{1}{2}\cdot \frac{a}{k^2} \cdot x^2+\frac{1}{2}}=f_{\frac{a}{k^{2}}}(x)$

Der entsprechende Graph stellt die Funktion $f_{\frac{a}{k^{2}}}$ der Schar dar.

b3)

Für $a=0$ ist der Graph von $f_{a}$ eine Gerade, also hat $f_{a}$ keine Wendestelle.

Für $a \neq 0$ gilt wegen des Satzes vom Nullprodukt:

$\left(a \cdot x^{2}-3\right) \cdot x=0$ gilt, wenn $x=0$ oder $a \cdot x^{2}-3=0$ ist. Also:

$\begin{array}[t]{rll} a \cdot x^{2}-3 &=& 0 &\quad \scriptsize \mid\; +3 \\[5pt] a \cdot x^{2} &=& 3&\quad \scriptsize \mid\; :a \neq 0\\[5pt] x^2&=& \frac{3}{a} \end{array}$

Da $x^2\geq 0$ ist für alle $x\in \mathbb{R}$ kann dies nur für positive Werte von $a$ erfüllt sein und hat dann zwei weitere Lösungen. Daraus folgt:

Für $a\lt0$ hat die vorgegebene Gleichung genau eine Lösung, also hat $f_{a}$ genau eine Wendestelle.

Für $a\gt0$ hat die vorgegebene Gleichung genau drei Lösungen, also hat $f_{a}$ genau drei Wendestellen.

c1)

1. Schritt: Notwendiges Kriterium für Extremstellen anwenden

Für eine lokale Extremstelle $x_E$ von $f_a$ muss $\(f_a$ gelten.

Mit dem Ableitungs- und dem solve-Befehl des CAS ergibt sich, dass $\(f_a$ lediglich für $a\gt 0$ lösbar ist. Die Lösungen sind dann $x_1 = -\frac{1}{\sqrt{a}}$ und $x_2 =\frac{1}{\sqrt{a}}.$

2. Schritt: Hinreichendes Kriterium für Extremstellen überprüfen

Mit dem CAS ergibt sich:

$\(f_a$

An der Stelle $x_1$ liegt also der einzige Tiefpunkt des Graphen von $f_a$ und an der Stelle $x_2$ der einzige Hochpunkt des Graphen von $f_a.$

3. Schritt: $\boldsymbol{y}$ -Koordinaten berechnen

Mit dem CAS ergibt sich:

$f_a\left(-\frac{1}{\sqrt{a}}\right) = -\frac{1}{\sqrt{a}}$

$f_a\left(\frac{1}{\sqrt{a}}\right) = \frac{1}{\sqrt{a}}$

Für alle Extrempunkte der Graphen von $f_a$ gilt also $y_E = x_E.$ Sie liegen also alle auf der Geraden zu $y=x.$

c2)

Da $v$ die Stelle des Hochpunkts des Graphen von $f_a$ ist, gilt mit den Ergebnissen aus c1) $f_a(v)=v.$

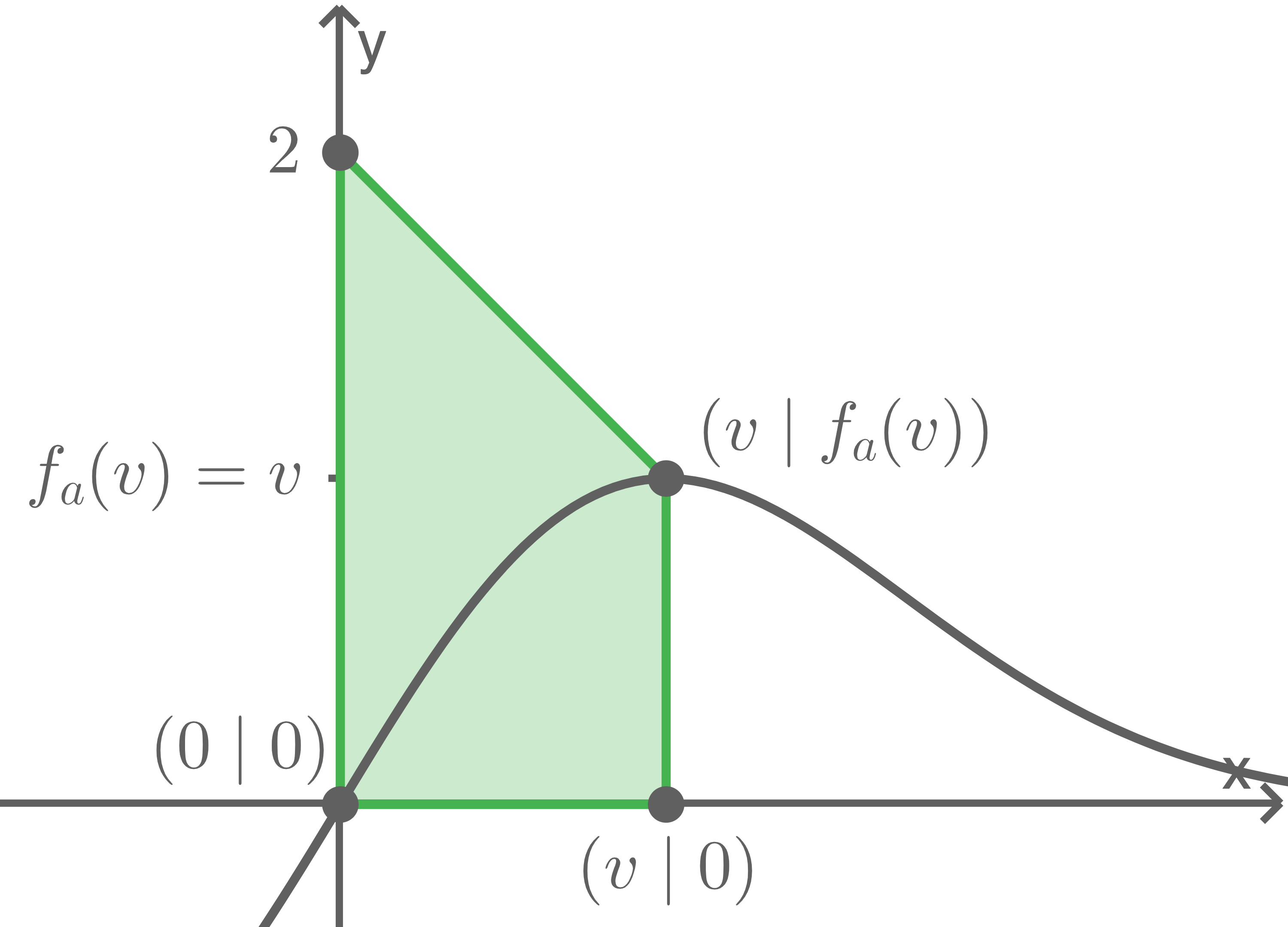Skizze Trapez - Schleswig-Holstein Abi CAS 2022 (Analysis 1)

Das Viereck hat also die Form eines Trapezes, bei dem die beiden zueinander parallelen Seiten die Längen $f_a(v)$ und $2$ haben und die Höhe $v$ beträgt.

Da $v$ eine Extremstelle von $f_a$ ist, gilt wegen c1) $f_a(v) = v = \frac{1}{}.$

Mit der Formel für den Flächeninhalt eines Trapezes gilt:

$\begin{array}[t]{rll} A_T &=& \dfrac{2 + f_a(v)}{2}\cdot v \\[5pt] &=& \dfrac{2 + v}{2}\cdot v \\[5pt] &=&\frac{1}{2}\cdot 2\cdot v+\frac{1}{2}\cdot v\cdot v \\[5pt] &=& v+ \frac{1}{2}v^2 \end{array}$

Gleichsetzen mit $144$ liefert mit dem CAS die Lösungen $v_1 = 16$ und $v_2=-18.$

Da $v$ eine Extremstelle von $f_a$ ist gilt ebenso $v=\frac{1}{\sqrt{a}}.$ Daher kommen nur positive Werte von $v$ infrage.

$\begin{array}[t]{rll} v&=& \frac{1}{\sqrt{a}} &\quad \scriptsize \mid\; \cdot \sqrt{a}\\[5pt] v\cdot \sqrt{a}&=& 1 &\quad \scriptsize \mid\; :v \\[5pt] \sqrt{a}&=& \frac{1}{v} &\quad \scriptsize \mid\;^2 \\[5pt] a &=& \frac{1}{v^2} \end{array}$

Einsetzen von $v= 16$ ergibt:

$a = \frac{1}{16^2}= \frac{1}{256}$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?