Analysis 2
Auf einer Waldfläche wurden neue Fichten gepflanzt. Alle Fichten hatten zum Zeitpunkt der Pflanzung eine Höhe von 
 verwendet. Dieser wird als Brusthöhendurchmesser (BHD) bezeichnet.
verwendet. Dieser wird als Brusthöhendurchmesser (BHD) bezeichnet.
a)
Betrachtet wird die Rate des Höhenwachstums der Fichten in Abhängigkeit von der Zeit.
Diese Wachstumsrate wird durch die Funktion mit
mit
 und
und  modellhaft beschrieben. Dabei ist
modellhaft beschrieben. Dabei ist  die seit der Pflanzung vergangene Zeit in Jahren und
die seit der Pflanzung vergangene Zeit in Jahren und  die Wachstumsrate in der Einheit Zentimeter pro Jahr
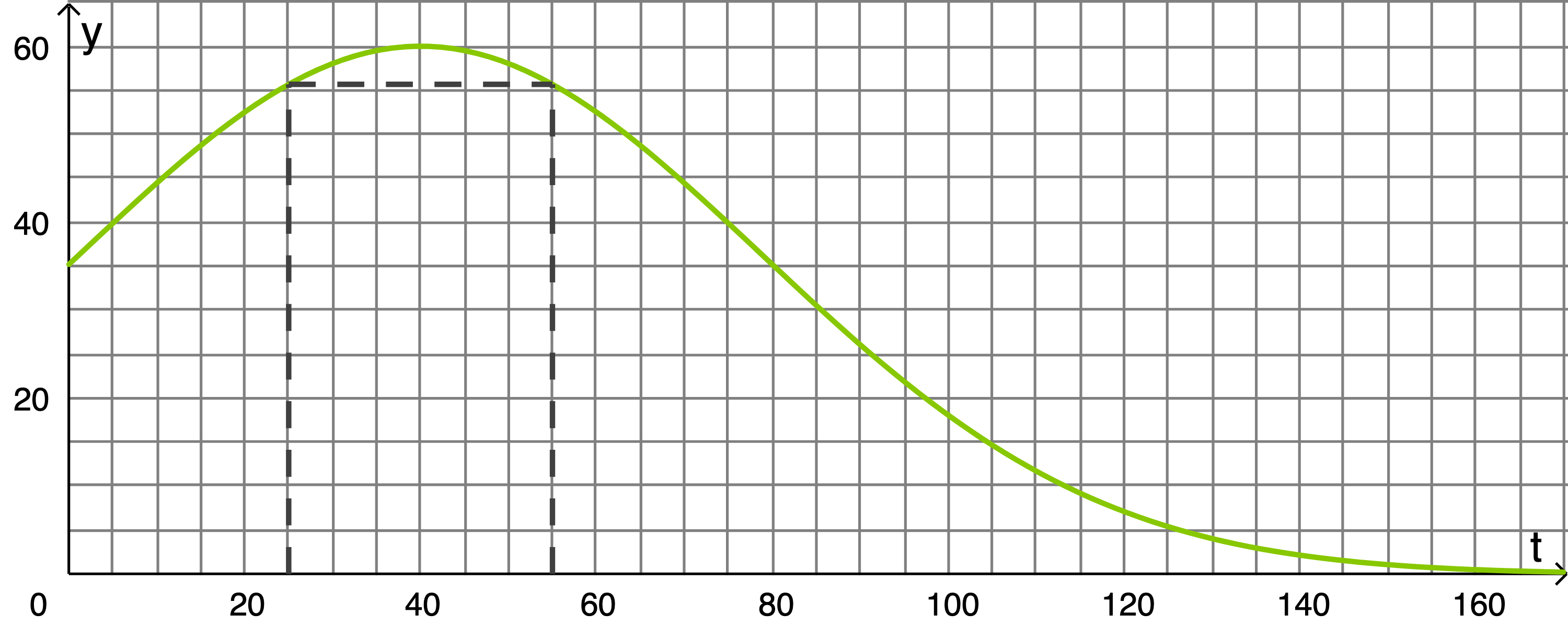
die Wachstumsrate in der Einheit Zentimeter pro Jahr  Die Abbildung zeigt den Graphen von
Die Abbildung zeigt den Graphen von 
Diese Wachstumsrate wird durch die Funktion

a1)
Zeige rechnerisch, dass die Wachstumsrate  Jahre nach Pflanzung am größten ist. Berechne den Zeitraum, in dem die Fichten mehr als
Jahre nach Pflanzung am größten ist. Berechne den Zeitraum, in dem die Fichten mehr als  wachsen.
wachsen.
(5 P)
a2)
Ein bestimmter Wert der Wachstumsrate wiederholt sich nach genau  Jahren.
Jahren.
Berechne die beiden zugehörigen Zeitpunkte.
Veranschauliche den Sachverhalt in der obigen Abbildung.
Berechne die beiden zugehörigen Zeitpunkte.
Veranschauliche den Sachverhalt in der obigen Abbildung.
(4 P)
a3)
Geben sie die Bedeutung des Terms  im Sachzusammenhang an und begründe deine Angabe.
im Sachzusammenhang an und begründe deine Angabe.
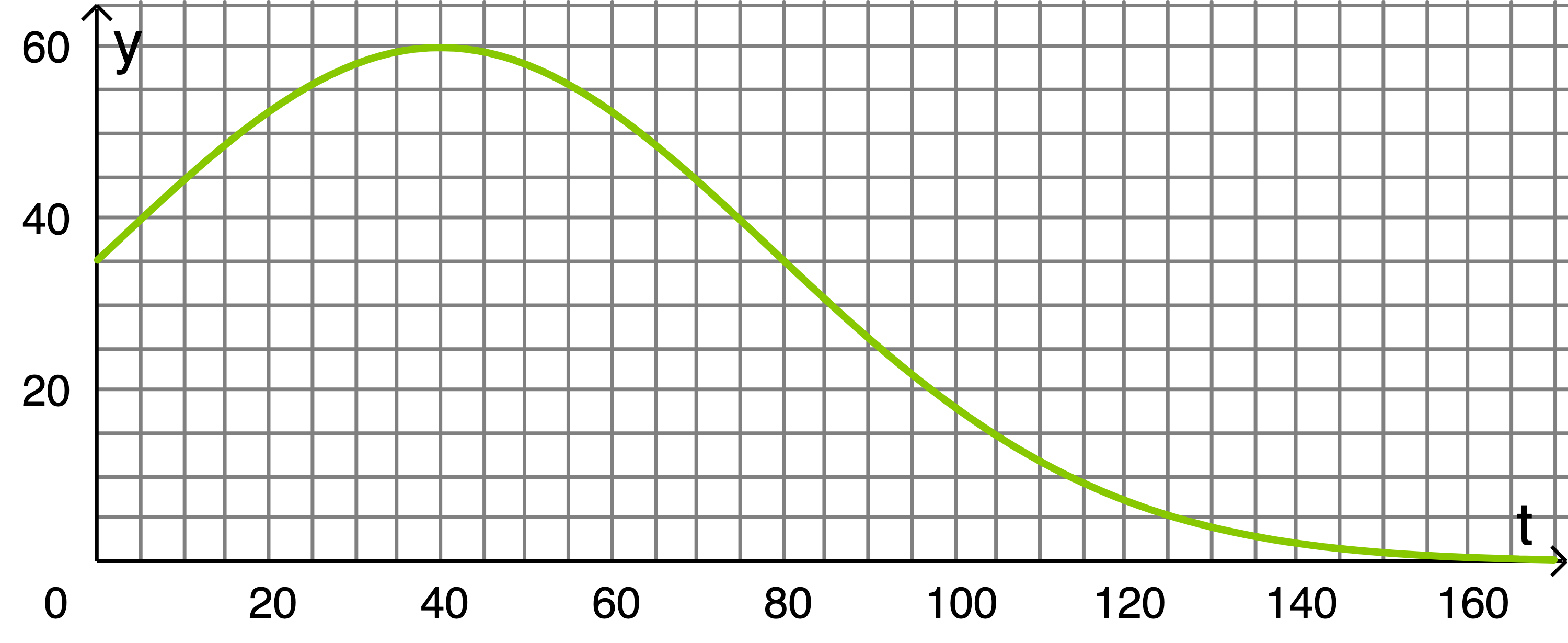
Skizziere die Höhe der Fichten in Abhängigkeit von der Zeit für die ersten Jahre nach der Pflanzung.
Jahre nach der Pflanzung.
Skizziere die Höhe der Fichten in Abhängigkeit von der Zeit für die ersten
(5 P)
b)
In einem anderen Modell wird die Höhe der Fichten in Abhängigkeit von der Zeit mit Hilfe der Funktion  mit
mit
 und
und  beschrieben. Dabei ist
beschrieben. Dabei ist  die seit der Pflanzung vergangene Zeit in Jahren und
die seit der Pflanzung vergangene Zeit in Jahren und  die Höhe in der Einheit Meter. Der Graph von
die Höhe in der Einheit Meter. Der Graph von  hat genau einen Wendepunkt
hat genau einen Wendepunkt 
Um den Verkaufswert eines Baumstamms zu bestimmen, wird dessen Durchmesser in einer Höhe von
b1)
Bestimme die Koordinaten von 
![\(\left[\text{Zur Kontrolle:} \,\ W(10\ln(99)\mid25)\right]\)](https://mathjax.schullv.de/6d67d256675f3a06dbd58b8557c05186e86068b4394995a112a274a35fb119ba?color=5a5a5a)
(3 P)
b2)
Eine Zeitschrift aus dem Jahr  enthält folgenden Textabschnitt:
"Von unseren einheimischen Bäumen steht die Fichte hinsichtlich ihres Höhenwachstums obenan, und zwar mit 37 Zentimetern durchschnittlich im Jahre. Doch sind von Forstbeamten Ausnahmen beobachtet worden, in denen Fichten in einem Jahre bis zu 150 Zentimeter ihrer Länge zusetzen."
enthält folgenden Textabschnitt:
"Von unseren einheimischen Bäumen steht die Fichte hinsichtlich ihres Höhenwachstums obenan, und zwar mit 37 Zentimetern durchschnittlich im Jahre. Doch sind von Forstbeamten Ausnahmen beobachtet worden, in denen Fichten in einem Jahre bis zu 150 Zentimeter ihrer Länge zusetzen."
 bestimmte maximale Wachstumsgeschwindigkeit mit der entsprechenden Angabe in diesem Textabschnitt.
bestimmte maximale Wachstumsgeschwindigkeit mit der entsprechenden Angabe in diesem Textabschnitt.
(Quelle: Walther Kabel: Wachstumsgeschwindigkeit bei Pflanzen. In: Das Buch für Alle. Jahrgang 1911, Heft 1, Union Deutsche Verlagsgesellschaft. Stuttgart 1911, S. 23.)
Vergleiche die durch die Funktion
(3 P)
b3)
Gib eine Gleichung der Tangente an den Graphen von  im Punkt
im Punkt  an.
an.
Die Höhe der Fichten kann im Zeitintervall von bis
bis  Jahren nach Pflanzung näherungsweise durch diese Tangente beschrieben werden.
Jahren nach Pflanzung näherungsweise durch diese Tangente beschrieben werden.
Bestimme die maximale prozentuale Abweichung im Vergleich zur Beschreibung mit Hilfe von
Die Höhe der Fichten kann im Zeitintervall von
Bestimme die maximale prozentuale Abweichung im Vergleich zur Beschreibung mit Hilfe von
(4 P)
c)
Für einen BHD ab  kann der Verkaufspreis von Fichtenstämmen in Abhängigkeit vom BHD näherungsweise mithilfe einer quadratischen Funktion bestimmt werden. Die Tabelle stellt für drei BHD den jeweiligen Preis dar.
kann der Verkaufspreis von Fichtenstämmen in Abhängigkeit vom BHD näherungsweise mithilfe einer quadratischen Funktion bestimmt werden. Die Tabelle stellt für drei BHD den jeweiligen Preis dar.
Ermittle den Preis für einen Fichtenstamm mit einem BHD von

Ermittle den Preis für einen Fichtenstamm mit einem BHD von

(4 P)
d)
Der BHD einer Fichte in Abhängigkeit von der Zeit  wird durch die Funktion
wird durch die Funktion  mit
mit
 und
und  modelliert. Dabei ist
modelliert. Dabei ist  die seit der Pflanzung vergangene Zeit in Jahren und
die seit der Pflanzung vergangene Zeit in Jahren und  der BHD in Metern.
der BHD in Metern.
d1)
Begründe, dass der BHD im Modell stets geringer als  ist.
ist.
(2 P)
d2)
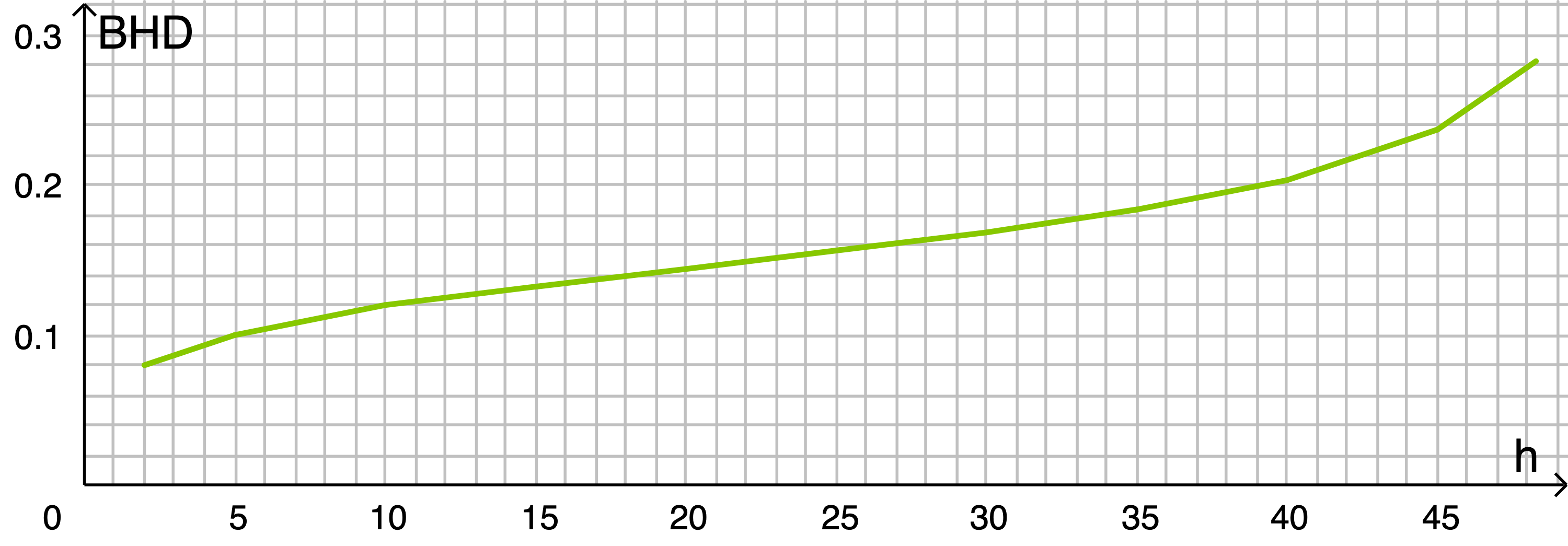
Zeichne für den Zeitraum zwischen 15 und 80 Jahren nach der Pflanzung einen Graphen, der den BHD in Abhängigkeit von der Höhe darstellt.
Verwende für die Höhe der Fichte das Modell aus der Aufgabe b).
Verwende für die Höhe der Fichte das Modell aus der Aufgabe b).
(4 P)
e)
Ein Fichtenstamm hat einen BHD von  Sein Volumen vom Boden bis zu einer Höhe von
Sein Volumen vom Boden bis zu einer Höhe von  beträgt
beträgt  Es soll davon ausgegangen werden, dass der Durchmesser des Stamms mit zunehmender Höhe linear abnimmt. Berechne den Durchmesser des Stamms in einer Höhe von
Es soll davon ausgegangen werden, dass der Durchmesser des Stamms mit zunehmender Höhe linear abnimmt. Berechne den Durchmesser des Stamms in einer Höhe von 
(6 P)
a1)
Maximum
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 Das notwendige Kriterium ist
Das notwendige Kriterium ist  Das hinreichende Kriterium für ein Maximum ist
Das hinreichende Kriterium für ein Maximum ist 
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II


 Das Maximum von
Das Maximum von  liegt bei
liegt bei  Wachstumszeitraum
Für
Wachstumszeitraum
Für  werden die Werte berechnet, für die
werden die Werte berechnet, für die  gilt:
gilt:
 Im ungefähren Zeitraum zwischen
Im ungefähren Zeitraum zwischen  und
und  Jahren liegt das Wachstum über
Jahren liegt das Wachstum über 
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

a2)
a3)
Mit dem Term lässt sich die Höhe der Fichte nach  Jahren in Metern berechnen.
Jahren in Metern berechnen.
Der Wert des Integrals gibt den Zuwachs der Fichte im Intervall von bis
bis  Jahren an, der mit der Ausgangsgröße von
Jahren an, der mit der Ausgangsgröße von  addiert wird. Durch die Multiplikation mit
addiert wird. Durch die Multiplikation mit  wird der Wert in Meter umgerechnet.
wird der Wert in Meter umgerechnet.
 Der Graph schneidet die
Der Graph schneidet die  Achse über
Achse über  da die Fichte bei der Pflanzung schon
da die Fichte bei der Pflanzung schon  groß ist.
groß ist.
Bei befindet sich ein Wendepunkt, da dort das Maximum des Wachstums in
befindet sich ein Wendepunkt, da dort das Maximum des Wachstums in  liegt.
liegt.
Der Graph besitzt eine waagerechte Asymptote, da die Fichte zwar immer weiter wächst, doch eine bestimmte Höhe nie überschreitet.
Der Wert des Integrals gibt den Zuwachs der Fichte im Intervall von

Bei
Der Graph besitzt eine waagerechte Asymptote, da die Fichte zwar immer weiter wächst, doch eine bestimmte Höhe nie überschreitet.
b1)
Die notwendige Bedingung für einen Wendepunkt ist 
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 Da der Graph von
Da der Graph von  laut Aufgabenstellung nur einen Wendepunkt besitzt, setzt man die Koordinate für
laut Aufgabenstellung nur einen Wendepunkt besitzt, setzt man die Koordinate für  in
in  ein.
ein.
 Der Wendepunkt liegt bei
Der Wendepunkt liegt bei 
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

b2)
Beim Wendepunkt besitzt  das größte Wachstum. Um den Wert zu berechnen wird der
das größte Wachstum. Um den Wert zu berechnen wird der  Wert von
Wert von  in
in  eingesetzt.
eingesetzt.
 TI nspire CAS
TI nspire CAS
 Casio Classpad II
Casio Classpad II
 Somit erreicht die Fichte, deren Wachstum mit
Somit erreicht die Fichte, deren Wachstum mit  definiert wird, nur ein Wachstum von
definiert wird, nur ein Wachstum von  und liegt damit unter dem maximalen Wachstum von
und liegt damit unter dem maximalen Wachstum von  , welches in der Zeitschrift angegeben ist.
, welches in der Zeitschrift angegeben ist.
menu  4: Analysis
4: Analysis  1: Ableitung
1: Ableitung
keyboard  Math2
Math2 

b3)
Die Steigung der Tangente am Punkt  wird mit
wird mit  berechnet.
berechnet.
Nutze dafür die Solve-Funktion deines CAS-Taschenrechners
 Die bekannten Werte werden in die Tangentengleichung eingesetzt.
Die Tangentengleichung lautet
Die bekannten Werte werden in die Tangentengleichung eingesetzt.
Die Tangentengleichung lautet  Da die Tangente die Höhe der Fichte im Intervall
Da die Tangente die Höhe der Fichte im Intervall ![\([40;50]\)](https://mathjax.schullv.de/4ff8c88ba7c9e004a8d81500742dc139e015776ec45fb82247aef74a78802431?color=5a5a5a) näherungsweise beschreibt, lässt sich die maximale Abweichung mit folgender Formel berechnen.
näherungsweise beschreibt, lässt sich die maximale Abweichung mit folgender Formel berechnen.
 Die Abweichung wird an einem der beiden Randstellen am größten sein.
Die Abweichung wird an einem der beiden Randstellen am größten sein.
 Die maximale Abweichung beträgt ca.
Die maximale Abweichung beträgt ca. 
Nutze dafür die Solve-Funktion deines CAS-Taschenrechners
c)
menu  3: Algebra
3: Algebra  7
7
keyboard  Math1
Math1 

d1)
Da  ist
ist  Der BHD ist also immer kleiner als
Der BHD ist also immer kleiner als 
d2)
Wenn man eine Wertetabelle für  und
und  anlegt, erhält man folgenden Graphen:
anlegt, erhält man folgenden Graphen:

e)
Das Volumen eines Kegelstumpfes lässt sich mit der Formel
 berechnen.
berechnen.
Gegeben sind BHD und
und 
 Da
Da  der Radius der Grundfläche ist, verwendest du
der Radius der Grundfläche ist, verwendest du  Nun kann die Abnahme des Radius des Stamms pro Meter Höhe berechnet werden.
Nun kann die Abnahme des Radius des Stamms pro Meter Höhe berechnet werden.
 Dieser Wert wird verwendet, um den Durchmesser in einer Höhe von
Dieser Wert wird verwendet, um den Durchmesser in einer Höhe von  zu berechnen.
zu berechnen.

 Der Durchmesser beträgt in
Der Durchmesser beträgt in  Höhe ca.
Höhe ca. 
Gegeben sind BHD