Hilfsmittelfreier Teil

HMF 1 - Analysis (Pool 1)

Die Abbildung zeigt den Graphen der auf $\mathbb{R}$ definierten Funktion $f$ .

Graph einer mathematischen Funktion im Koordinatensystem mit Achsenbeschriftung.

Abb. 1

1.1

Bestimme mithilfe der Abbildung einen Näherungswert für $\displaystyle\int_{3}^{5}\;\mathrm f(x)\; dx$ .

(2P)

Die Funktion $F$ ist die auf $\mathbb{R}$ definierte Stammfunktion von $f$ mit $F(3)=0$ .

1.2

Gib mithilfe der Abbildung einen Näherungswert für die Ableitung von $F$ an der Stelle 2 an.

(1P)

1.3

Zeige, dass $F(b)=\displaystyle\int_{3}^{b}\;\mathrm f(x)\; dx$ mit $b\in \mathbb{R}$ gilt.

(2P)

HMF 2 - Analysis (Pool 1)

Gegeben ist die Funktion $f$ durch $f(x)=x^2\cdot\; \mathrm e^{2-x}$ .

2.1

Zeige, dass $f‘(3)=-\dfrac{3}{\mathrm e}$ gilt.

(2P)

2.2

Bestimme eine Gleichung der Tangente $t$ an den Graphen der Funktion $f$ an der Stelle 3.

(3P)

HMF 3 - Analytische Geometrie (Pool 1)

Betrachtet wird der abgebildete Würfel $ABCDEFGH$ . Die Eckpunkte $D$ , $E$ , $F$ und $H$ dieses Würfels besitzen in einem kartesischen Koordinatensystem die folgenden Koordinaten:
$D(0\;|\;0\;|\;-2)$ , $E(2\;|\;0\;|\;0)$ , $F(2\;|\;2\;|\;0)$ und $H(0\;|\;0\;|\;0)$

Diagramm eines Quaders mit beschrifteten Ecken A bis H.

Abb. 2

3.1

Zeichne in die Abbildung die Koordinatenachsen ein und bezeichne diese. Gib die Koordinaten des Punktes $A$ an.

(2P)

3.2

Der Punkt $P$ liegt auf der Kante $\overline{FB}$ des Würfels und hat vom Punkt $H$ den Abstand $3$ . Berechne die Koordinaten des Punktes $P$ .

(3P)

HMF 4 - Analytische Geometrie (Pool 1)

Gegeben sind die Ebene $E: 2x_1+x_2+2x_3=6$ sowie die Punkte $P(1\;|\;0\;|\;2)$ und $Q(5\;|\;2\;|\;6)$ .

4.1

Zeige, dass die Gerade durch die Punkte $P$ und $Q$ senkrecht zur Ebene $E$ verläuft.

(2P)

4.2

Die Punkte $P$ und $Q$ liegen symmetrisch zu einer Ebene $F$ . Ermittle eine Gleichung von $F$ .

(3P)

HMF 5 - Analytische Geometrie (Pool 2)

Gegeben sind die Punkte $A(-2\;|\;1\;|\;4)$ und $B(-4\;|\;0\;|\;6)$ .

5.1

Bestimme die Koordinaten des Punktes $C$ so, dass gilt: $\overrightarrow{CA}=2\cdot\overrightarrow{AB}$ .

(2P)

5.2

Durch die Punkte $A$ und $B$ verläuft die Gerade $g$ . Betrachtet werden Geraden, für welche die Bedingungen I und II gelten:

$g$

$A$

$3$

Ermittle eine Gleichung für eine dieser Geraden.

(3P)

HMF 6 - Stochastik (Pool 1)

Anna und Björn leben in einer Wohngemeinschaft. Sie bestellen regelmäßig Waren über das Internet. Für einen Zustellversuch eines Paketboten werden die folgenden Ereignisse betrachtet:

$A$

$B$

Gegeben ist die folgende Vierfeldertafel:

	$B$	$\overline{B}$
$A$	$0,1$	$x$
$\overline{A}$			$0,7$
	$0,6$		$1$

6.1

Bestimme den Wert von $x$ und gib das zugehörige Ereignis sowohl in der Mengenschreibweise als auch in Worten an.

(3P)

6.2

Berechne die Wahrscheinlichkeiten dafür, dass Björn zu Hause ist, wenn Anna nicht zu Hause ist.

(2P)

HMF 7 - Stochastik (Pool 1)

Bei einem Zufallsexperiment wird eine ideale Münze so lange geworfen, bis zum zweiten Mal Zahl ( $Z$ ) oder zum zweiten Mal Wappen ( $W$ ) oben liegt.
Als Ergebnismenge wird { $ZZ; WW; ZWZ; ZWW; WZZ; WZW$ } festgelegt.

7.1

Begründe, dass dieses Zufallsexperiment kein Laplace-Experiment ist.

(2P)

7.2

Die Zufallsgröße $X$ ordnet jedem Ergebnis die Anzahl der entsprechenden Münzwürfe zu. Berechne den Erwartungswert von $X$ .

(3P)

HMF 8 - Stochastik (Pool 2)

Eine Zufallsgröße $X$ ist binomialverteilt mit der Erfolgswahrscheinlichkeit $p$ und dem Stichprobenumfang $n=2$ .

8.1

Berechne für $p=0,4$ die Wahrscheinlichkeit $P(X\leq1)$ .

(2P)

8.2

Zeige, dass für jeden Wert von $p$

$P(X\neq0)+P(X\neq1)+P(X\neq2)=2$ gilt.

(3P)

Bildnachweise [nach oben]

[1]

[2]

HMF 1 - Analysis

1.1

$\blacktriangleright$ Näherungswert für Integral bestimmen (1. Möglichkeit)

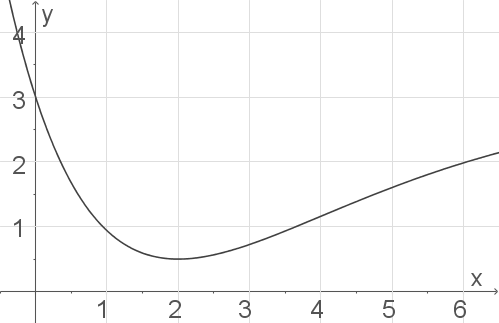
Du sollst in diesem Aufgabenteil das Integral mit der unteren Integralgrenze $3$ und der oberen Integralgrenze $5$ näherungsweise mithilfe der Abbildung bestimmen. Das Integral ist gerade der Flächeninhalt der zwischen der Funktion $f$ und der $x$ -Achse zwischen $3$ und $5$ eingeschlossen wird. Zähle also die Kästchen die sich in diesem Bereich befinden. Dabei entspricht ein Kästchen $0,25$ Flächeneinheiten.

Im Bereich zwischen $3$ und $5$ befinden sich ungefähr $9$ Kästchen. Um nun den Wert des Integral zu bestimmen, musst du $9$ mit $0,25$ multiplizieren, um den Wert des Integrals angeben zu können.

$9 \cdot 0,25 = 2,25.$

Somit hat das Integral $\displaystyle \int_3^5 f(x) \,\mathrm dx$ ungefähr den Wert $2,25.$

$\blacktriangleright$ Näherungswert für Integral bestimmen (2. Möglichkeit)

Anstatt die Kästchen im Bereich zwischen $3$ und $5$ zu zählen, kannst du das Integral auch mithilfe eines Trapezes annähern. Der Flächeninhalt $A_{Trapez}$ ist durch folgende Formel gegeben:

$A_{Trapez} = \dfrac{a+c}{2} \cdot h.$

$a$ und $c$ bezeichnen die Längen der Seiten und $h$ die Höhe des Trapezes.

Folglich gilt für das gesuchte Integral $I$

$\begin{array}[t]{rll} I &=& \dfrac{f(3)+f(5)}{2} \cdot 2 \\[5pt] &\approx& \dfrac{0,7 + 1,7}{2} \cdot 2 \\[5pt] &=& 2,4. \end{array}$

Somit hat das Integral $\displaystyle \int_3^5 f(x) \,\mathrm dx$ mit der Näherung durch ein Trapez ungefähr den Wert $2,4.$

1.2

$\blacktriangleright$ Ableitung von $\boldsymbol{F}$ an der Stelle 2 angeben

$F$ ist eine Stammfunktion der Funktion $f$ , d.h. der Wert von $f$ an der Stelle $x$ gibt gerade die Ableitung von $F$ an der Stelle $x$ an. Du musst also den Wert $f(2)$ in der Abbildung ablesen.

$f(2) \approx 0,5.$

Demnach ist die Ableitung der Funktion $F$ an der Stelle $2$ ungefähr $0,5$ .

1.3

$\blacktriangleright$ Wert des $\boldsymbol{\displaystyle \int_3^b f(x)}$ dx berechnen

Wenn du ein Integral $\displaystyle \int_a^b f(x) \,\mathrm dx$ gegeben hast, gilt nach dem Hauptsatz der Differential- und Integralrechnung

$\displaystyle \int_a^b f(x) \,\mathrm dx = F(b) - F(a).$

$F$ bezeichnet dabei die Stammfunktion von $f$ .

Nach Voraussetzung ist $F(3) = 0$ , sodass für das Integral $\displaystyle \int_3^b f(x) \,\mathrm dx$ gilt:

$\begin{array}[t]{rll} \displaystyle \int_3^b f(x) \,\mathrm dx &=& F(b) - F(3) \\[5pt] &=& F(b) - 0 \\[5pt] &=& F(b). \end{array}$

Demnach ist der Wert des Integrals $\displaystyle \int_3^b f(x) \,\mathrm dx$ für beliebige $b \gt 3$ gleich $F(b)$ .

HMF 2 - Analysis

2.1

$\blacktriangleright$ Ableitung an der Stelle $\boldsymbol{3}$ bestimmen

Gegeben hast du die Funktion $f(x) = x^2 \cdot \mathrm e^{2-x}$ . Als erstes bestimmt du die allgemeine Ableitung $f‘(x)$ mithilfe der Produktregel. Hast du eine Funktion der Form $f(x) = u(x) \cdot v(x)$ gegeben, so besagt die Produktregel, dass die Ableitung der Funktion durch

$f‘(x)= u‘(x)\cdot v(x) + u(x)\cdot v‘(x).$

gegeben ist.

In diesem Fall ist $u(x) = x^2$ und $v(x) = \mathrm e^{2-x}.$ Demnach lautet die Ableitung

$\begin{array}[t]{rll} f‘(x) &=& 2x \cdot \mathrm e^{2-x} + x^2 \cdot (-\mathrm e^{2-x}) \\[5pt] &=& \mathrm e^{2-x} \cdot (2x - x^2). \end{array}$

Setze nun die entsprechenden Stelle in die Ableitung ein, um den Wert der Ableitung an dieser Stelle zu erhalten.

$\begin{array}[t]{rll} f‘(3) &=& \mathrm e^{2-3} \cdot (2 \cdot 3 - 3^2) \\[5pt] &=& \mathrm e^{-1} \cdot (6-9) \\[5pt] &=& \dfrac{-3}{\mathrm e} \end{array}$

Die Ableitung an der Stelle $3$ ist also gleich $\dfrac{-3}{\mathrm e}$ .

2.2

$\blacktriangleright$ Gleichung der Tangente $\boldsymbol{t}$ an der Stelle $\boldsymbol{3}$ bestimmen

Die Tangente $t$ ist eine Gerade, d.h. sie besitzt die Form

$t:$ $y = mx + c.$

Dabei ist $m$ die Steigung der Tangente und $c$ der Ordinatenabschnitt, also der Wert an dem die Tangente die $y$ -Achse schneidet.

Du hast die Steigung $m$ an der Stelle $3$ in der ersten Teilaufgabe bestimmt. Weiterhin weißt du, dass der Punkt $(3 \mid\ f(3))$ auf der Geraden liegen muss. Somit ist die einzig gesuchte Größe der Ordinatenabschnitt $c$ . Du formst also die obere Gleichung nach $c$ um und setzt die bekannten Werte ein.

$\begin{array}[t]{rll} y &=& mx + c &\quad \scriptsize \mid\; -mx \\[5pt] c &=& y - mx \\[5pt] &=& f(3) + \dfrac{3}{\mathrm e} \cdot 3 \\[5pt] &=& 3^2 \cdot \mathrm e^{2-3} + \dfrac{9}{\mathrm e} \\[5pt] &=& \dfrac{18}{\mathrm e} \end{array}$

Der gesuchte Ordintenabschnitt ist somit $c=\dfrac{18}{\mathrm e}$ . Die Gleichung der Tangente $t$ lautet demnach

$y = \dfrac{-3}{\mathrm e} x + \dfrac{18}{\mathrm e}.$

HMF 3 - Analytische Geometrie

3.1

$\blacktriangleright$ Koordinatenachsen zeichnen

Der Punkt $H$ hat die Koordinaten $(0 \mid 0 \mid 0)$ , d.h. der Ursprung des Koordinatensystems liegt in $H$ . Da der Punkt $E$ als erste Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die $x$ -Achse die Gerade $EH$ . Die Richtung der $x$ -Achse ist dabei die Richtung des Vektors $\overrightarrow{HE}$ . Das Vorgehen bei der $y$ -Achse ist analog. Da der Punkt $G$ als zweite Koordinate eine positive Zahl hat und die restlichen Koordinaten gleich Null sind, ist die $y$ -Achse die Gerade $GH$ . Die Richtung der $y$ -Achse ist dabei die Richtung des Vektors $\overrightarrow{HG}$ . Der Punkt $D$ hat als letzte Koordinate eine negative Zahl (die restlichen Koordinaten sind gleich Null), das bedeutet, dass die $z$ -Achse die Gerade $DH$ ist. Die Richtung ist dieses Mal allerdings die Richtung des Vektors $\overrightarrow{DH}$ .

Somit ergibt sich folgendes Koordinatensystem:

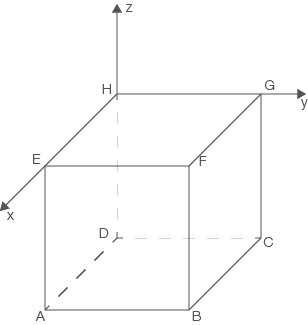3D-Darstellung eines Würfels mit Achsenbeschriftungen x, y und z.

Abb. 1: Würfel im Koordinatensystem

Der Punkt $A$ hat demnach die Koordinaten $(2 \mid 0 \mid -2).$

3.2

$\blacktriangleright$ Punkt $\boldsymbol{P}$ bestimmen

Sind zwei Punkte $P_1(x_1 \mid y_1 \mid z_1)$ und $P_2(x_2 \mid y_2 \mid z_2)$ gegeben, so ist der Abstand $\boldsymbol{d}$ der beiden Punkte definiert als

$\boldsymbol{d = \sqrt{(x_1-x_2)^2 + (y_1 - y_2)^2 + (z_1 - z_2)^2}}.$

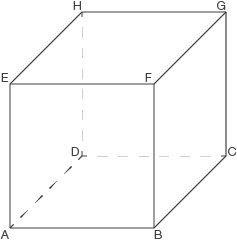
Der Punkt $P$ soll auf der Kante $\overline{FB}$ des Würfels liegen und soll zum Punkt $H$ (dem Ursprung des Koordinatensystems) den Abstand $3$ haben, d.h. $d=3$ . Die Koordinaten des zweiten Punkts $H$ sind gegeben. Die Koordinaten des ersten Punkts $P$ kannst du mithilfe des Ortvektors von $F$ und dem Vektor $\overrightarrow{FB}$ umschreiben.

$P = \overrightarrow{OF} + \lambda \cdot \overrightarrow{FB} = \pmatrix{2 \\ 2 \\ 0} + \lambda \cdot \pmatrix{0 \\ 0 \\ -2}$ mit $0 \leq \lambda \leq 1.$

Setze nun die Koordinaten der Punkte in die Formel für den Abstand mit $d=3$ ein und löse die Gleichung nach $\lambda$ auf

$\begin{array}[t]{rll} 3 &=& \sqrt{(2 + 0 \cdot \lambda - 0)^2 + (2 + 0 \cdot \lambda - 0)^2 + (0 - 2 \lambda - 0)^2} \\[5pt] &=& \sqrt{4 + 4 + 4 \lambda^2} &\quad \scriptsize \mid\ ^2 \\[5pt] 9 &=& 4 + 4 + 4 \lambda^2 &\quad \scriptsize \mid\ -8 \\[5pt] 1 &=& 4 \lambda^2 &\quad \scriptsize \mid\ :4 \\[5pt] \lambda^2 &=& \dfrac{1}{4} &\quad \scriptsize \mid\ \sqrt{\,} \\[5pt] \lambda &=& \pm \dfrac{1}{2} \end{array}$

Da für $\lambda = -\dfrac{1}{2}$ der Punkt $P$ nicht auf der Kante $\overline{FB}$ liegen würde, muss $\lambda = \dfrac{1}{2}$ sein. Für $\overrightarrow{OP}$ gilt somit

$\overrightarrow{OP} = \pmatrix{2 \\ 2 \\ 0} + \dfrac{1}{2} \cdot \pmatrix{0 \\ 0 \\ -2} = \pmatrix{2 \\ 2 \\ -1}.$

Somit sind die Koordinaten von $P(2 \mid 2 \mid -1).$

HMF 4 - Analytische Geometrie

4.1

$\blacktriangleright$ Nachweisen, dass die Gerade orthogonal zur Ebene ist

Du musst in dieser Aufgabe zeigen, dass die Gerade, die durch die Punkte $P$ und $Q$ geht, orthogonal zur Ebene $E$ ist. Da die Ebenengleichung in Koordinatenform angegeben ist, ist die einfachste Möglichkeit, den Normalenvektor an der Koordinatenform abzulesen und zeigen, dass dieser Vektor mit dem Vektor $\overrightarrow{PQ}$ linear abhängig ist.

Wenn du eine Ebene mit der Koordinatenform $ax_1 + bx_2 + cx_3 = d$ gegeben hast, lautet der Normalenvektor $\overrightarrow{n}$

$\overrightarrow{n} = \pmatrix{a \\ b \\ c}.$

Folglich lautet der Normalenvektor $\overrightarrow{n}$ der gegebenen Ebene $\overrightarrow{n} = \pmatrix{2 \\ 1 \\ 2}.$

Im nächsten Schritt berechnest du den Vektor $\overrightarrow{PQ}.$

$\begin{array}[t]{rll} \overrightarrow{PQ} &=& \overrightarrow{OQ} - \overrightarrow{OP} \\[5pt] &=& \pmatrix{5 \\ 2 \\ 6} - \pmatrix{1 \\ 0 \\ 2} \\[5pt] &=& \pmatrix{4 \\ 2 \\ 4}. \end{array}$

Die beiden Vektoren $\overrightarrow{n}$ und $\overrightarrow{PQ}$ sind linear abhängig, da $2 \cdot \pmatrix{2 \\ 1 \\ 2} = \pmatrix{4 \\ 2 \\ 4}$ .

Somit steht die Ebene $E$ senkrecht zur Geraden $PQ$ .

4.2

$\blacktriangleright$ Gleichung der Ebene $\boldsymbol{F}$ ermitteln

Die Punkte $P$ und $Q$ liegen symmetrisch zur Ebene $F$ , d.h. der Vektor $\overrightarrow{PQ}$ ist ein Normalenvektor der Ebene $F$ . Somit lautet die Koordinatenform der Ebene $F:$ $4x_1 + 2x_2 + 4x_3 = d$ .

Um nun das fehlende $d$ zu bestimmen, musst du die Koordinaten eines Punkt der Ebene $F$ in die Koordinatenform einsetzen.

Da $P$ und $Q$ symmetrisch zur Ebene $F$ sind, liegt der Mittelpunkt $M$ der Strecke $\overline{PQ}$ in der Ebene $F$ . Der Ortsvektor von $M$ ist demnach.

$\begin{array}[t]{rll} \overrightarrow{OM} &=& \overrightarrow{OP} + \dfrac{1}{2} \cdot \overrightarrow{PQ} \\[5pt] &=& \pmatrix{1 \\ 0 \\ 2} + \dfrac{1}{2} \cdot \pmatrix{4 \\ 2 \\ 4} \\[5pt] &=& \pmatrix{3 \\ 1 \\ 4}. \end{array}$

Der Punkt $M$ hat also die Koordinaten $(3 \mid\ 1 \mid\ 4).$ Setzte diese in die Koordinatenform, um das gesuchte $d$ zu bekommen.

$\begin{array}[t]{rll} d &=& 4 \cdot 3 + 2 \cdot 1 + 4 \cdot 4 \\[5pt] &=& 30. \\[5pt] \end{array}$

Die Koordinatenform der Ebene $F$ lautet also $4x_1 + 2x_2 + 4x_3 = 30$ bzw. $2x_1 + x_2 + 2x_3 = 15$ , wenn man die Gleichung durch $2$ teilt.

HMF 5 - Analytische Geometrie

5.1

$\blacktriangleright$ Koordinaten von $\boldsymbol{C}$ bestimmen

Gesucht ist ein Punkt $C$ , der die Bedingung $\overrightarrow{CA} = 2 \cdot \overrightarrow{AB}$ erfüllt. Du berechnest also zuerst den Vektor

$\overrightarrow{AB} = \pmatrix{-4 \\ 0 \\ 6} - \pmatrix{-2 \\ 1 \\ 4} = \pmatrix{-2 \\ -1 \\ 2}$ ,

um ihn anschließend in die Gleichung einzusetzen.

$\begin{array}[t]{rll} \pmatrix{-2 - c_1 \\ 1 - c_2 \\ 4 - c_3} &=& 2 \cdot \pmatrix{-2 \\ -1 \\ 2} \\[5pt] &=& \pmatrix{-4 \\ -2 \\ 4} \end{array}$

Somit folgt $c_1 = 2$ , $c_2 = 3$ und $c_3 = 0$ . Der gesuchte Punkt $C$ hat also die Koordinaten $(2 \mid 3 \mid 0).$

5.2

$\blacktriangleright$ Gerade $\boldsymbol{h}$ bestimmen

Gesucht ist eine Gerade $h$ , die die zwei Bedingungen $I$ und $II$ erfüllt. Bestimme also zuerst einen Vektor $\vec{t}$ , der die Bedingung $I$ erfüllt, um anschließend einen Aufpunkt $P$ für die Gerade $h$ auf der Geraden $g$ zu finden, der den Abstand $3$ zum Punkt $A$ hat.

1.Schritt: Vektor $\boldsymbol{\vec{t}}$ bestimmen

Der Vektor $\vec{t}$ muss orthogonal zu $\overrightarrow{AB}$ liegen, d.h. das Skalarprodukt dieser beiden Vektoren muss null sein.

$\begin{array}[t]{rll} 0 &=& \overrightarrow{AB} \circ \vec{t} \\[5pt] &=& -2t_1 - t_2 + 2t_3 \end{array}$

Wähle $t_1 = 1$ und $t_2=0$ , sodass für $t_3$ automatisch $t_3 = 1$ folgt.

Somit ist $\vec{t} = \pmatrix{1 \\ 0 \\ 1}$ und orthogonal zu $\overrightarrow{AB}$ .

2.Schritt: Aufpunkt für die Gerade $\boldsymbol{h}$ finden

Der Aufpunkt $P$ der gesuchten Gerade $h$ muss auf der Geraden $g$ liegen und den Abstand $3$ zum Punkt $A$ haben. Somit gibt es zwei mögliche Kandidaten für den Punkt $P$ , denn die Kugel mit dem Mittelpunkt $A$ und dem Radius $3$ schneidet $g$ in zwei Punkten.

Folglich muss der Richtungsvektor $\pmatrix{-2 \\ -1 \\ 2}$ vom Punkt $A$ aus $3$ Einheiten lang sein.

$\begin{array}[t]{rll} 3 &=& \left| \lambda \cdot \pmatrix{-2 \\ -1 \\ 2} \right| \\[5pt] &=& \sqrt{(-2\lambda)^2 + (-\lambda)^2 + (2\lambda)^2} \\[5pt] &=& \sqrt{9 \lambda^2} \\[5pt] &=& \pm 3 \lambda \end{array}$

Somit kann $\lambda$ entweder $1$ oder $-1$ sein.

Wähle $\lambda = 1$ und bestimme die Koordinaten von $P$ .

$\begin{array}[t]{rll} \overrightarrow{OP}&=& \overrightarrow{OA} + 1 \cdot \pmatrix{-2 \\ -1 \\ 2} \\[5pt] &=& \pmatrix{-2 \\ 1 \\ 4} + 1 \cdot \pmatrix{-2 \\ -1 \\ 2} \\[5pt] &=& \pmatrix{-4 \\ 0 \\ 6}. \end{array}$

Demnach hat $P$ die gleichen Koordinaten wie der Punkt $B$ .

3.Schritt: Geradengleichung aufstellen

Nun hast du alle notwendigen Informationen berechnet, um die Geradengleichung von $h$ aufzustellen. Du benutzt als Aufpunkt den Punkt $P$ und als Richtungsvektor $\overrightarrow{t}$ .

$h:$ $\pmatrix{-4 \\ 0 \\ 6}+ \lambda \cdot \pmatrix{1 \\ 0 \\ 1}$

Bemerkung: Beachte, dass es hier unendlich viele Lösungen gibt. Du kannst den Richtungsvektor der Gerade $h$ auch anders wählen und für den Aufpunkt $P$ gibt es zwei Möglichkeiten.

HMF 6 - Stochastik

6.1

$\blacktriangleright$ Wert für $\boldsymbol{x}$ bestimmen

Die Variable $x$ beschreibt, dass Ereignis „ $A \cap \overline{B}$ “, also dass Anna zu Hause ist (Ereignis $A$ ) und das Björn nicht zu Hause ist (Ereignis $\overline{B}$ ).

Um diesen Wert zu bestimmen, vervollständigst du die letzt Spalte der Vierfeldertafel, sodass du eine Gleichung bekommst, die du nach $x$ auflösen kannst.

Die gesuchte Zahl, die im leeren Feld der letzten Spalte stehen soll, muss mit $0,7$ $1$ ergeben. Somit steht im ersten Feld der letzten Spalte $0,3$ .

Die Addition von $0,1$ und $x$ muss $0,3$ ergeben.

$0,1 + x = 0,3.$

Demzufolge ist $x = 0,2$ .

	$B$	$\overline{B}$
$A$	$0,1$	$0,2$	$0,3$
$\overline{A}$			$0,7$
	$0,6$		$1$

6.2

$\blacktriangleright$ Wahrscheinlichkeit berechnen

Nun wird vorausgesetzt, dass Anna nicht zu Hause ist. Gesucht ist die Wahrscheinlichkeit, dass unter dieser Bedigung Björn zu Hause ist, d.h. $P(B \mid\ \overline{A})$ muss berechnet werden.

Sind zwei Ereignisse $C$ und $D$ gegeben, so ist die bedingte Wahrscheinlichkeit von $C$ , dabei wird $D$ vorausgesetzt, gegeben durch

$P(C \mid\ D) = \dfrac{P(C \cap D)}{P(D)}.$

Die Wahrscheinlichkeit, dass Björn zu Hause ist unter der Bedingung, dass es Anna nicht ist, beträgt also:

$\begin{array}[t]{rll} P(B \mid\ \overline{A}) &=& \dfrac{P(B \cap \overline{A})}{P(\overline{A})} \\[5pt] &=& \dfrac{P(B \cap \overline{A})}{0,7} \end{array}$

$P(B \cap \overline{A})$ kannst du mithilfe der Vierfeldertafel bestimmen.

$\begin{array}[t]{rll} P(B \cap \overline{A}) &=& 0,6 - 0,1 \\[5pt] &=& 0,5. \end{array}$

Demnach ist die gesuchte Wahrscheinlichkeit

$\begin{array}[t]{rll} P(B \mid\ \overline{A}) &=& \dfrac{0,5}{0,7} \\[5pt] &=& \dfrac{5}{7}. \end{array}$

Björn ist also mit einer Wahrscheinlichkeit von $P(B \mid\ \overline{A}) = \dfrac{5}{7}$ zu Hause, unter der Voraussetzung, dass Anna nicht zu Hause ist.

HMF 7 - Stochastik

7.1

$\blacktriangleright$ Begründen des Zufallsexperiments

In dieser Teilaufgabe musst du begründen, dass es sich nicht um ein Laplace-Experiment handelt.

Bei einem Laplace-Experiment müssen alle Ausprängungen, also die möglichen Ergebnisse, mit gleicher Wahrscheinlichkeit auftreten.

Betrachtest du $P(\{ ZZ\}) = \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{4}$ und $P(\{ ZWZ\}) = \dfrac{1}{2} \cdot \dfrac{1}{2} \cdot \dfrac{1}{2} = \dfrac{1}{8}$ , so stellt du fest, dass die Wahrscheinlichkeiten dieser zweier Ergebnisse verschieden sind.

Somit handelt es sich nicht um ein Laplace-Experiment.

7.2

$\blacktriangleright$ Erwartungswert von $\boldsymbol{X}$ berechnen

Sei $X$ eine Zufallsvariable, die die Werte $X = x_{i}$ für $i=1, \dots n$ annehmen kann und $P(X = x_i)$ die dazugehörigen Wahrscheinlichkeiten. Dann gilt für den Erwartungswert von $X$

$E(X) = x_1 \cdot P(X=x_1) + x_2 \cdot P(X=x_2) + \dots + x_n \cdot P(X=x_n).$

In dieser Teilaufgabe beschreibt $X$ die Anzahl der Würfe, d.h. $X$ kann nur die Werte $2$ oder $3$ annehmen.

Berechne also die Wahrscheinlichkeiten für $X=2$ und $X=3.$

$\begin{array}[t]{rll} P(X=2)&=& P(\{ ZZ \}) + P(\{ WW \}) \\[5pt] &=& \dfrac{1}{4} + \dfrac{1}{4} \\[5pt] &=& \dfrac{1}{2}. \end{array}$

Da $X$ nur zwei Werte annehmen kann, folgt für $P(X=3)$ automatisch

$\begin{array}[t]{rll} P(X=3)&=& 1 - P(X=2) \\[5pt] &=& 1 - \dfrac{1}{2} \\[5pt] &=& \dfrac{1}{2}. \end{array}$

Jetzt kannst du alle Werte in die Formel für den Erwartungswert einsetzen

$\begin{array}[t]{rll} E(X)&=& 2 \cdot P(X=2) + 3 \cdot P(X=3) \\[5pt] &=& 2 \cdot \dfrac{1}{2} + 3 \cdot \dfrac{1}{2} \\[5pt] &=& 2,5. \end{array}$

Der Erwarungswert der Zufallsvariablen $X$ beträgt also $2,5$ .

HMF 8 - Stochastik

8.1

$\blacktriangleright$ Wahrschenlichkeit $\boldsymbol{P(X \leq 1)}$ berechnen

In diesem Aufgabenteil benötigst du die Binomialverteilung . Die Formel für $n$ Versuche, $k$ Erfolge und der Wahrscheinlichkeit $p$ bei einem Versuch einen Erfolg zu erzielen lautet

$B_{n,p}(k)$ = $\binom{n}{k}\cdot p^k \cdot (1-p)^{n-k}.$

Gesucht ist Wahrscheinlichkeit dafür, bei zwei Versuchen und der Erfolgswahrscheinlichkeit $p = 0,4$ höchstens einen Erfolg zu erzielen, also entweder $X = 0$ oder $X = 1.$ Setzt also die entsprechenden Werte in die Formel für die Binomialverteilung ein, um $P(X \leq 1)$ zu bestimmen.

$\begin{array}[t]{rll} P(X \leq 1) &=& P(X = 0 ) + P(X = 1) \\[5pt] &=& \binom{2}{0}\cdot 0,4^0 \cdot (1-0,4)^{2-0} + \binom{2}{1}\cdot 0,4^1 \cdot (1-0,4)^{2-1} \\[5pt] &=& 0,36 + 0,48 \\[5pt] &=& 0,84 \\[5pt] &=& 0,84 \% \end{array}$

Die Wahrscheinlichkeit bei zwei Versuchen höchstens einen Erfolg zu erzielen, liegt bei $84 \%.$

8.2

$\blacktriangleright$ Gleichung für beliebiges $\boldsymbol{p}$ zeigen

Du musst nun zeigen, dass für ein beliebiges $0 \leq p \leq 1$ die Gleichung

$P(X \neq 0) + P(X \neq 1) + P(X \neq 2) = 2$

erfüllt ist.

Schreibe $P(X \neq 0)$ , $P(X \neq 1)$ und $P(X \neq 2)$ um und fasse anschließend zusammen.

$\begin{array}[t]{rll} P(X \neq 0) + P(X \neq 1) + P(X \neq 2) &=& (P(X = 1) + P(X = 2)) + (P(X = 0) + P(X = 2)) \\[5pt] & & + (P(X = 0) + P(X = 1)) \\[5pt] &=& 2 \cdot (P(X = 0) + P(X = 1) + P(X = 2)) \\[5pt] &=& 2 \cdot 1 \\[5pt] &=& 2. \end{array}$

Die vorgegebene Gleichung ist also für alle $p$ erfüllt.

Bildnachweise [nach oben]

[1]