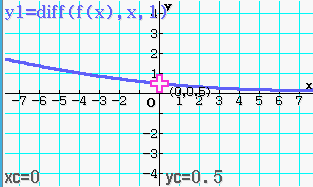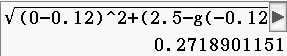Analysis Aufgabe 2
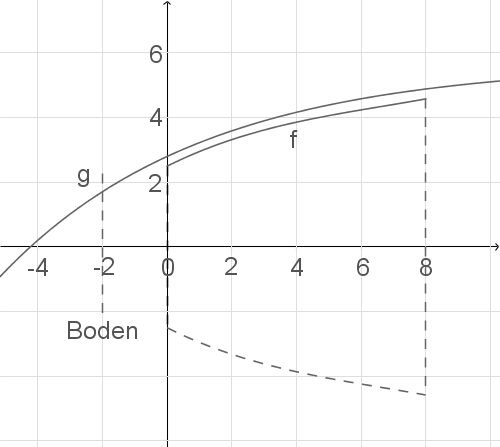
Die Abbildung zeigt den Längsschnitt des inneren Randes eines rotationssymmetrischen Glases. Eine Einheit entspricht einem Zentimeter in der Wirklichkeit.
Die obere Begrenzung des Längsschnittes des inneren Randes des Glases kann durch den Graphen einer ganzrationalen Funktion mit
mit  im Intervall
im Intervall ![\([0;8]\)](https://mathjax.schullv.de/f865209a1807ce5fbc790d415dc19a6fa37135ca31f3a6fa1f42441652d095e7?color=5a5a5a) beschrieben werden.
beschrieben werden.
Die obere Begrenzung des Längsschnittes des inneren Randes des Glases kann durch den Graphen einer ganzrationalen Funktion
a)
Die obere Begrenzung des Längsschnittes des äußeren Randes des Glases soll durch den Graphen einer Funktion  mit
mit  im Intervall
im Intervall ![\([-1;8]\)](https://mathjax.schullv.de/cc3f407c296f2acd059d5660963c355c53ec90117d2c8905ffc9b6b90b260a68?color=5a5a5a) beschrieben werden. Der Graph verläuft durch die Punkte
beschrieben werden. Der Graph verläuft durch die Punkte  ,
,  und
und  .
.
 .
.
- Bestimme eine Funktionsgleichung von
.
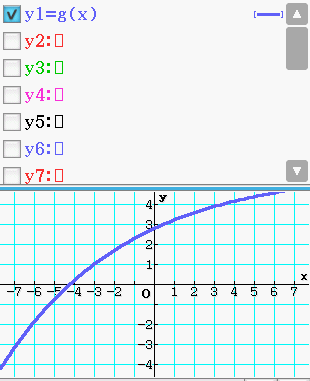
- Skizziere den Graphen der Funktion
in der obigen Abbildung.
- Berechne die kleinste und die größte in
-Richtung gemessene Dicke der Glaswand im Intervall
.
- Berechne das für die Herstellung des gesamten Glases benötigte Volumen des Glasmaterials. Der Boden ist durchgängig eben.
(14P)
b)
Der Graph der Funktion  hat einen Wendepunkt
hat einen Wendepunkt  . Ein Auffüllen des aufrecht stehenden Glases bis zu diesem Punkt macht einen guten optischen Eindruck.
. Ein Auffüllen des aufrecht stehenden Glases bis zu diesem Punkt macht einen guten optischen Eindruck.
- Gib die zugehörige Füllhöhe an.
- Begründe, dass die Gleichung
im Intervall
(6P)
c)
Ausgehend von einem beliebigen Punkt  auf der Innenrandkurve soll die Dicke des Glases in Richtung der Normalen zum Graphen von
auf der Innenrandkurve soll die Dicke des Glases in Richtung der Normalen zum Graphen von  , also senkrecht zur Tangente an der Stelle
, also senkrecht zur Tangente an der Stelle  , gemessen werden.
, gemessen werden.
- Zeige, dass bei diesem Verfahren nie in
-Richtung gemessen wird.
- Berechne die Dicke der Glaswand ausgehend vom Punkt
(9P)
d)
In einem Labor mit der Raumtemperatur  wird ein Heißgetränk in das Glas gefüllt.
wird ein Heißgetränk in das Glas gefüllt.  gibt die Temperatur des Heißgetränkes in
gibt die Temperatur des Heißgetränkes in  an; dabei beschreibt
an; dabei beschreibt  die Zeit in Minuten nach Messbeginn.
die Zeit in Minuten nach Messbeginn.
Zu Beginn ( ) beträgt die Temperatur des Heißgetränkes
) beträgt die Temperatur des Heißgetränkes  . Die momentane Änderungsrate der Temperatur
. Die momentane Änderungsrate der Temperatur  ist durch
ist durch
 gegeben.
gegeben.
Zu Beginn (
- Berechne die Temperaturabnahme in den ersten 60 Minuten.
- Bestimme
.
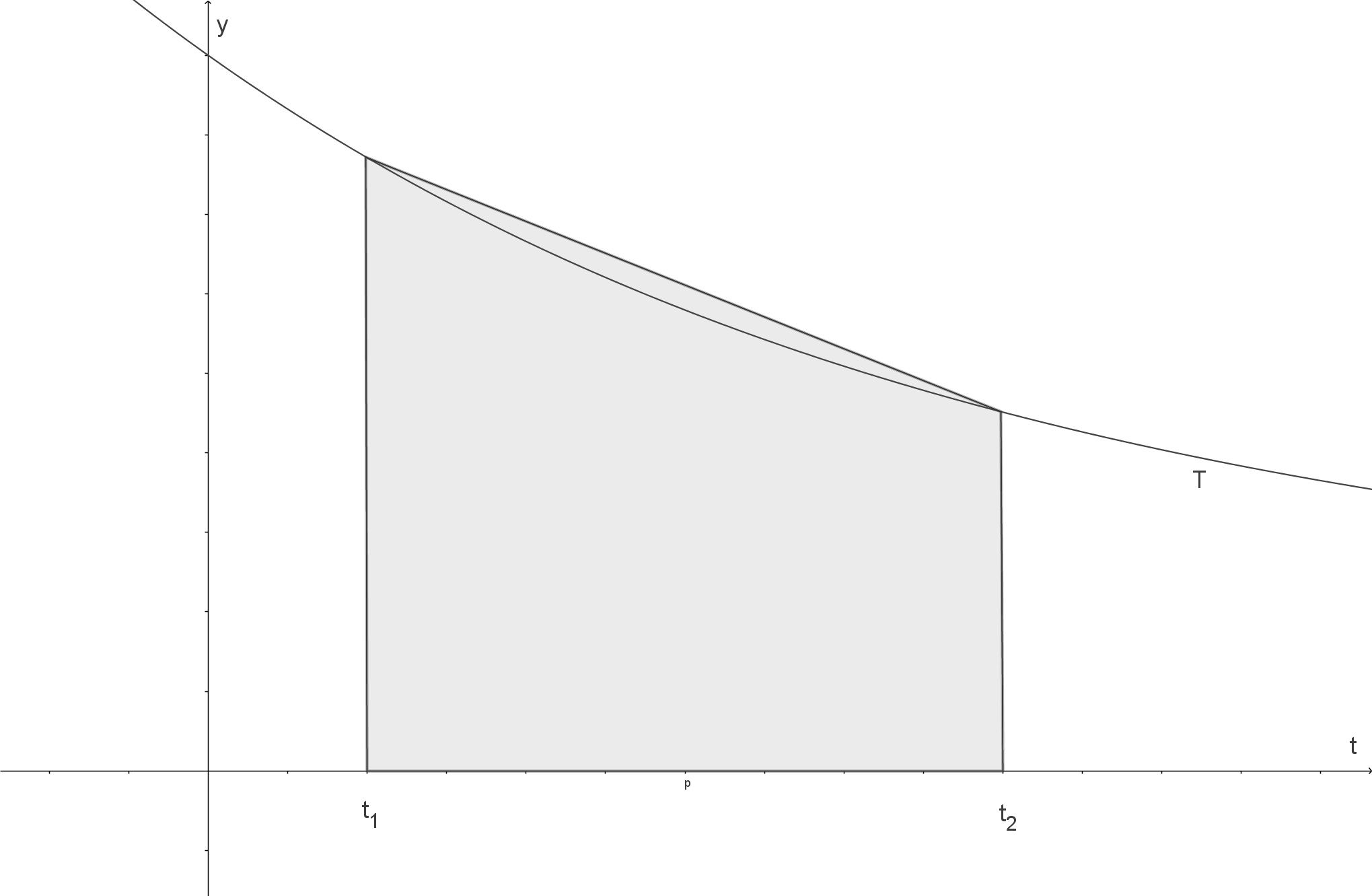
- Begründe unter Verwendung der folgenden Abbildung, dass für jedes Zeitintervall
mit
die durchschnittliche Temperatur in diesem Intervall kleiner ist als der arithmetische Mittelwert der Temperaturen
und
.
(11P)
Bildnachweise [nach oben]
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
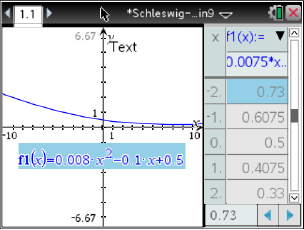
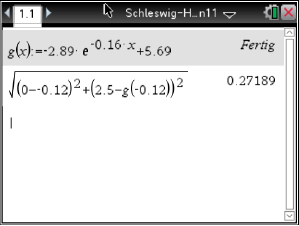
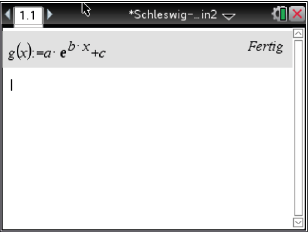 Abb. 1: g(x) im CAS abspeichern
Abb. 1: g(x) im CAS abspeichern
menu 
 : Algebra
: Algebra 
 : Gleichungssystem lösen
: Gleichungssystem lösen 
 : Gleichungssystem lösen...
: Gleichungssystem lösen...
Du kannst nun eingeben, wie viele Gleichungen es gibt. Da du drei Punkte gegeben hast, kannst du als Anzahl auch drei Gleichungen eingeben. Im nächsten Schritt sollst du die Anzahl der Unbekannten eingeben. Wenn du die Funktion 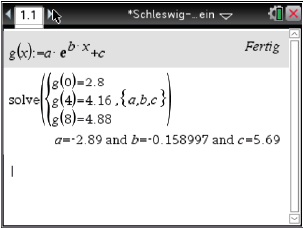 Abb. 2: Gleichungssystem
Abb. 2: Gleichungssystem
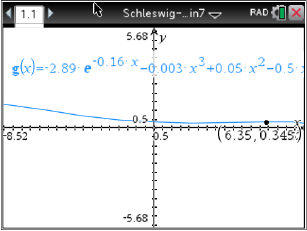 Abb. 6: Maximum
Abb. 6: Maximum
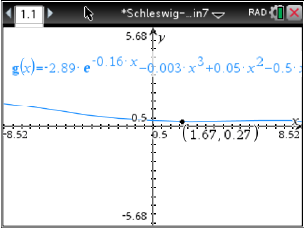 Abb. 7: Minimum
Abb. 7: Minimum
 Abb. 8: Volumen des benötigten Glases
Abb. 8: Volumen des benötigten Glases
b)
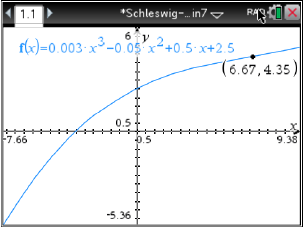 Abb. 9: Wendestelle
Abb. 9: Wendestelle
c)
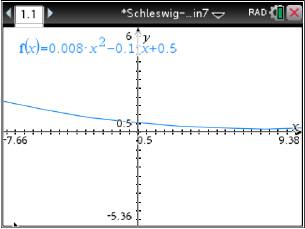 Abb. 10: Dicke des Glases
Abb. 10: Dicke des Glases
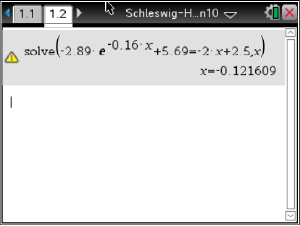 Abb. 12: Schnittstelle bestimmen
Abb. 12: Schnittstelle bestimmen
d)
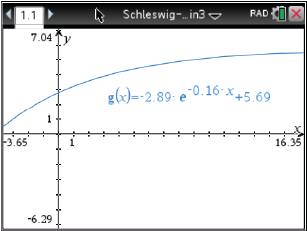
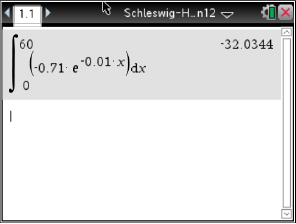 Abb. 14: Temperaturänderung
Abb. 14: Temperaturänderung
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
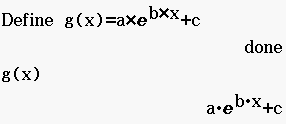 Abb. 1: g(x) im CAS abspeichern
Abb. 1: g(x) im CAS abspeichern
Keyboard  Math1
Math1
Du kannst nun eingeben, wie viele Gleichungen es gibt. Da du drei Punkte gegeben hast, kannst du als Anzahl auch drei Gleichungen eingeben. Im nächsten Schritt sollst du die Anzahl der Unbekannten eingeben. Wenn du die Funktion 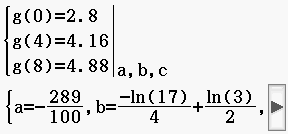 Abb. 2: Gleichungssystem
Abb. 2: Gleichungssystem
Analyse  Graphische Lösung
Graphische Lösung  Maximum
Maximum
Du erhältst folgendes Schaubild, auf dem du nun den 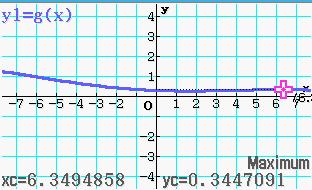 Abb. 6: Maximum
Abb. 6: Maximum
Analyse  Graphische Lösung
Graphische Lösung  Minimum
Minimum
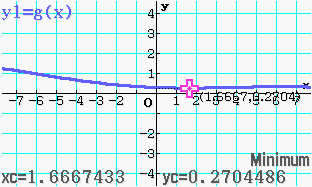 Abb. 7: Minimum
Abb. 7: Minimum
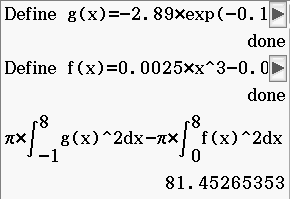 Abb. 8: Volumen des benötigten Glases
Abb. 8: Volumen des benötigten Glases
b)
Analyse  Graphische Lösung
Graphische Lösung  Wendepunkt
Wendepunkt
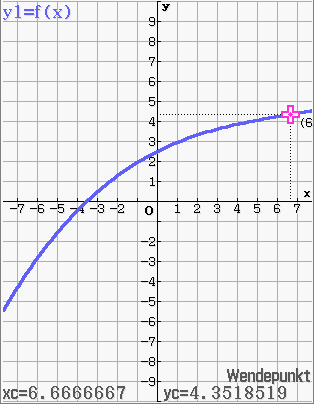 Abb. 9: Wendestelle
Abb. 9: Wendestelle
c)
Analyse  Graphische Lösung
Graphische Lösung  Nullstelle
Nullstelle
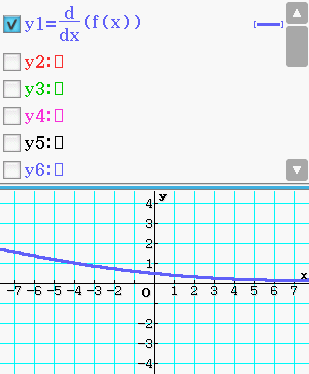 Abb. 10: Dicke des Glases
Abb. 10: Dicke des Glases
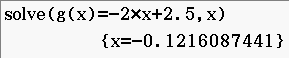 Abb. 12: Schnittstelle bestimmen
Abb. 12: Schnittstelle bestimmen
d)
Analyse  Graphische Lösung
Graphische Lösung  Nullstelle
Nullstelle
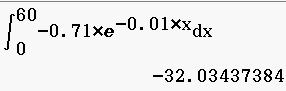 Abb. 14: Temperaturänderung
Abb. 14: Temperaturänderung
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.