Hilfsmittelfreier Teil

HMF 1 - Stochastik (Pool 1)

Für ein Zufallsexperiment mit den beiden Ereignissen $A$ und $B$ gilt
$P(A)=0,6$ und $P(\overline{B})=0,3$ sowie $P(A\cap \overline {B})=0,2.$

1.1

Erstelle für die beschriebene Situation eine vollständige Vierfeldertafel.

(3 P)

1.2

Bestimme die Wahrscheinlichkeit $P_A(\overline{B}).$

(2 P)

HMF 2 - Stochastik (Pool 1)

Die Abbildung zeigt das Netz eines Würfels.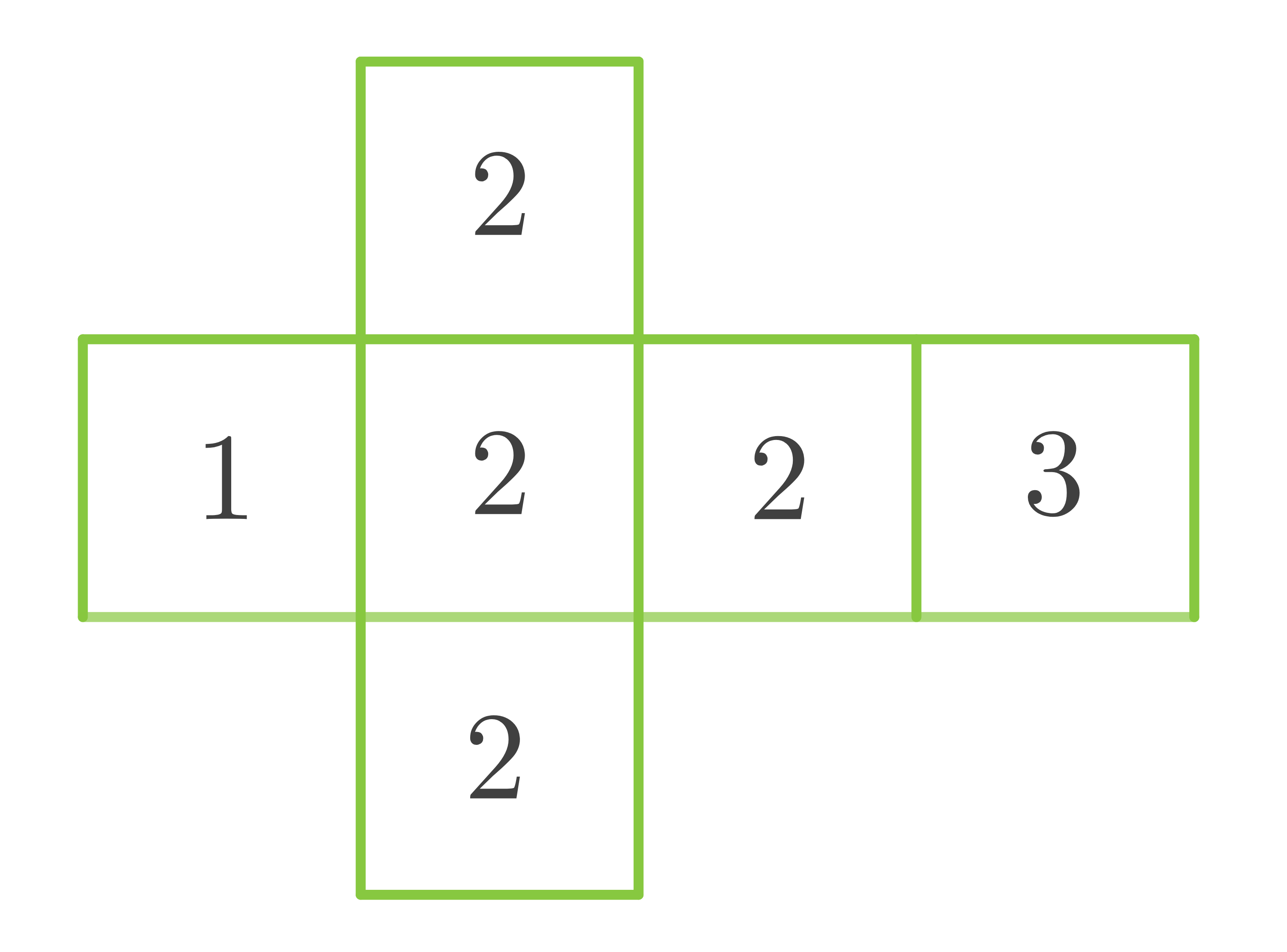

Ein Diagramm mit Zahlen in Kästchen, angeordnet in einer Kreuzform.

2.1

Der Würfel wird zweimal geworfen. Berechne die Wahrscheinlichkeit dafür, dass die Summe der beiden geworfenen Zahlen $4$ ist.

(2 P)

2.2

Die Zahlen $"1"$ und $"3"$ werden jeweils durch eine neue Zahl ersetzt. Das Verhältnis der beiden neuen Zahlen ist ebenfalls $1 : 3.$ Betrachtet man bei einmaligem Werfen des geänderten Würfels die geworfene Zahl, so ist der zugehörige Erwartungswert $4.$
Ermittle die beiden neuen Zahlen.

(3 P)

HMF 3 - Analytische Geometrie (Pool 1)

Gegeben ist eine Kugel $K$ mit

$K:(x_1-4)^2+(x_2-4)^2+(x_3-1)^2=1.$

3.1

Gib die Koordinaten des Mittelpunktes $M$ und den Radius $r$ der Kugel $K$ sowie die Koordinaten eines Punktes $P$ auf dieser Kugel an.

(2 P)

3.2

Gegeben sind die Punkte $A(4\mid4\mid0)$ und $B(0\mid8\mid0).$
Zeige, dass die Gerade durch $A$ und $B$ die Kugel $K$ in genau einem Punkt berührt.

(3 P)

HMF 4 - Analytische Geometrie (Pool 1)

In einem Koordinatensystem ist ein gerader Zylinder mit dem Radius $5$ und der Höhe $10$ gegeben, dessen Grundfläche in der $x_1x_2$ -Ebene liegt.

$M(8\mid5\mid10)$ ist der Mittelpunkt der Deckfläche.

4.1

Weise nach, dass der Punkt $P(5\mid1\mid0)$ auf dem Rand der Grundfläche des Zylinders liegt.

(2 P)

4.2

Unter allen Punkten auf dem Rand der Deckfläche hat der Punkt $S$ den kleinsten Abstand von $P$ , der Punkt $T$ den größten.

Gib die Koordinaten von $S$ an und bestimme die Koordinaten von $T.$

(3 P)

HMF 5 - Analytische Geometrie (Pool 2)

Für jedes $a \in \mathbb{R}$ sind die Geraden $g_a$ und $h_a$ gegeben durch

$g_a:\overrightarrow{x}=\pmatrix{1\\1\\1}+r\cdot\pmatrix{a\\4\\1}$ und $h_a:\overrightarrow{x}=\pmatrix{1\\1\\1}+s\cdot\pmatrix{2a\\a\\2}.$

Die Geraden $g_a$ und $h_a$ haben den gemeinsamen Punkt $P(1\mid1\mid1).$

5.1

Untersuche, ob es ein $a\in\mathbb{R}$ gibt, für das $g_a$ und $h_a$ sogar identisch sind.

(2 P)

5.2

Zeige, dass es genau ein $a\in\mathbb{R}$ derart gibt, so dass $g_a$ und $h_a$ orthogonal zueinander sind.

(3 P)

HMF 6 - Analysis (Pool 1)

Gegeben ist die Funktion $f$ mit $f(x)=\dfrac{1}{5}x^5+x^4-\dfrac{8}{3}x^3$ mit $x\in\mathbb{R}.$

6.1

Berechne die lokale Änderungsrate der Funktion an der Stelle $x=-1.$

(2 P)

6.2

Die Funktion $f$ hat drei Wendestellen. Bestimme diese Stellen.

(3 P)

HMF 7 - Analysis (Pool 1)

Die Abbildung zeigt den Graphen der Funktion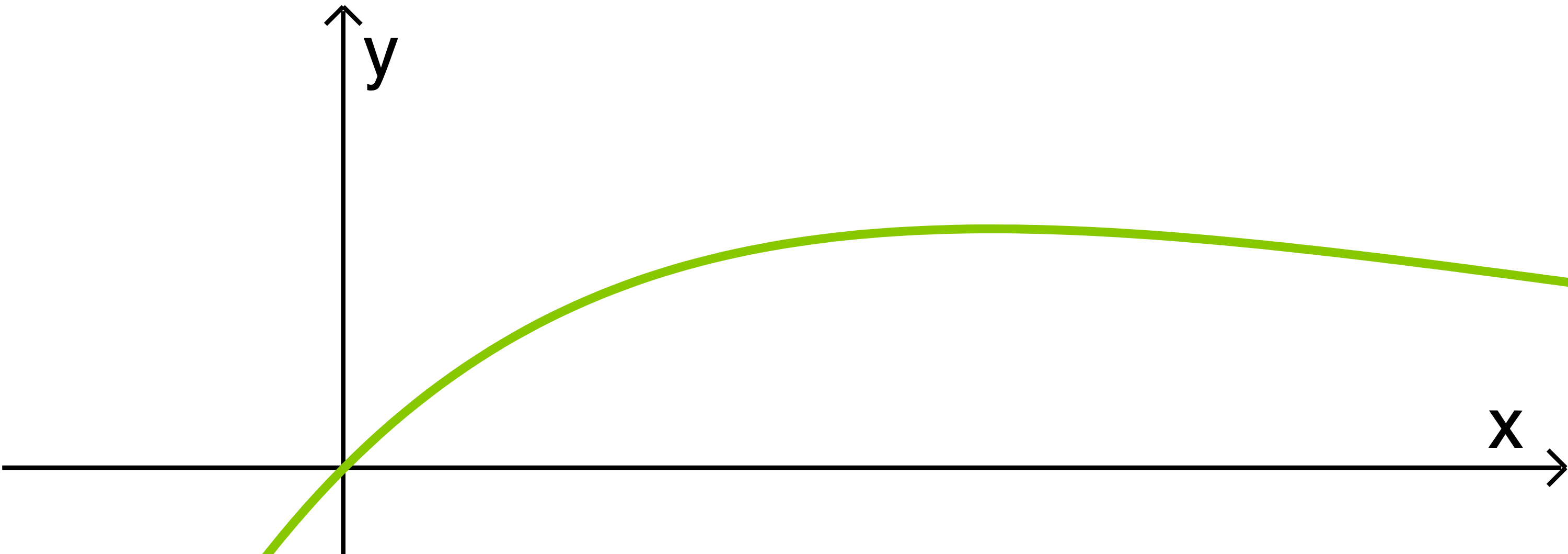 $f$ mit $f(x)=x\cdot \mathrm e^{-x}$ und $x\in\mathbb{R}.$ Betrachtet werden die Dreiecke mit den Eckpunkten $O(0\mid0)$ , $P(a\mid0)$ und $Q(a\mid f(a))$ mit $a>0.$

Graph einer mathematischen Funktion mit grünem Verlauf, x- und y-Achse beschriftet.

7.1

Begründe, dass der Flächeninhalt jedes dieser Dreiecke mit dem Term $\dfrac{1}{2}a^2\mathrm e^{-a}$ bestimmt werden kann.

(2 P)

7.2

Unter den betrachteten Dreiecken hat eines den größten Flächeninhalt.
Bestimme den zugehörigen Wert $a.$

(3 P)

HMF 8 - Analysis (Pool 2)

Für jeden Wert von $a\in\mathbb{R}\setminus \{0\}$ ist eine Funktion $f_a$ gegeben mit $f_a(x)=a\cdot(x-2)^3$ und $x\in\mathbb{R}.$

8.1

Zeige, dass die in $\mathbb{R}$ definierte Funktion $F$ mit $F(x)=\frac{1}{2}\cdot(x-2)^4+3$ eine Stammfunktion von $f_2$ ist.

(1 P)

8.2

Untersuche mithilfe von Skizzen, für welche Werte von $a$ sich unter den Stammfunktionen von $f_a$ solche befinden, die nur negative Funktionswerte haben.

(4 P)

1.1

	$A$	$\overline{A}$	Gesamt
$B$	$0,4$	$0,3$	$0,7$
$\overline{B}$	$0,2$	$0,1$	$0,3$
Gesamt	$0,6$	$0,4$	$1$

1.2

$P_A(\overline B)=\dfrac{P(A\cap\overline B)}{P(A)}=\dfrac{0,2}{0,6}=\dfrac{1}{3}=33,33\,\%$

2.1

Mögliche Kombinationen sind:
$2$ mit $2$
und $1$ mit $3.$

$P(2-2)=\dfrac{4}{6}\cdot\dfrac{4}{6}$ $=\dfrac{4}{9}$

$P(1-3)=\dfrac{1}{6}\cdot\dfrac{1}{6}\cdot2$ $=\dfrac{1}{18}$

$P(2-2)+P(1-3)=\dfrac{8}{18}+\dfrac{1}{18}$ $=\dfrac{9}{18}=50\,\%$

Die Wahrscheinlichkeit für das Ergebnis von $4,$ beträgt $50\,\%.$

2.2

Ersetze die beiden neuen Zahlen durch $x$ und $y$ . Da diese im Verhältnis 1:3 stehen, gilt $x=3\cdot y.$
Nun kannst du den Erwartungswert aufstellen und passend auflösen.

$\begin{array}[t]{rll} \mu&=& \dfrac{1}{6}\cdot x+\dfrac{4}{6}\cdot2+\dfrac{1}{6}\cdot y&\quad \scriptsize \mid\;x =3y \\[5pt] 4&=& \dfrac{1}{6}\cdot 3y+\dfrac{8}{6}+\dfrac{1}{6}\cdot y&\quad \scriptsize \mid\;-\dfrac{8}{6} \\[5pt] \dfrac{8}{3}&=& \dfrac{4}{6} \cdot y&\quad \scriptsize \\[5pt] 4&=&y \end{array}$

$\begin{array}[t]{rll} x&=& 3y&\quad \scriptsize \mid\; y=4\\[5pt] x&=&12 \end{array}$

Durch Einsetzen erschließt sich, dass die neuen Zahlen $4$ und $12$ sind.

3.1

$P(4\mid4\mid2)$ besitzt den Abstand $1$ von $M(4\mid4\mid1)$ und da $r=1$ ist, liegt $P$ auf der Kugel.

3.2

Die Gerade $g$ durch $A$ und $B$ kann durch folgende Gleichung beschrieben werden:

$g:\,\ \overrightarrow{x}=\pmatrix{4\\4\\0}+s\cdot\pmatrix{-4\\4\\0}$ in $K.$

$g$ wird in $K$ eingesetzt, um die Schnittpunkte zu berechnen:

$s=0$

Vollständige Lösung anzeigen

$\pmatrix{4\\4\\0}+0\cdot\pmatrix{-4\\4\\0}=\pmatrix{4\\4\\0}$

$g$ ist eine Tangente von $K$ und schneidet die Kugel nur bei $S(4\mid4\mid0).$

4.1

$M_D(8\mid5\mid10)$ ist der Mittelpunkt der Deckfläche des Zylinders. $M_G(8\mid5\mid0)$ der Mittelpunkt der Grundfläche und wird dadurch bestimmt, dass die Höhe des Zylinders $10$ ist.

Die Kreisgleichung der Grundfläche lautet somit $K_G:(x_1-8)^2+(x_2-5)^2+(x_3-0)^2=5^2.$

Punkt $P$ wird in $K_G$ eingesetzt:

$25=25$

Vollständige Lösung anzeigen

$P$ liegt auf $K_G.$

4.2

$S(5\mid1\mid10)$ liegt direkt über $P$ auf dem Rand der Deckfläche des Zylinders.
$T$ ist der am Punkt $M_D$ gespiegelte Punkt von $S$ .

$\overrightarrow{T}=\overrightarrow{0S}+2\cdot\overrightarrow{SM_D}$

$\overrightarrow{T} =\pmatrix{5\\1\\10}+2\cdot\pmatrix{8-5\\5-1\\10-10}$

$\overrightarrow{T}=\pmatrix{5\\1\\10}+\pmatrix{6\\8\\0}$

$\overrightarrow{T}=\pmatrix{11\\9\\10}$

$T(11\mid9\mid10)$ ist auf dem Rand der Deckfläche am weitesten von $P$ entfernt.

5.1

Da die Stützvektoren bereits identisch sind, müssen nur noch die Richtungsvektoren linear abhängig sein. Es muss also $a$ so gewählt werden, dass ein $x\in\mathbb{R}$ gibt mit:

$\pmatrix{2a\\a\\2}=x\cdot\pmatrix{a\\4\\1}$

$a=8$

Vollständige Lösung anzeigen

Bei $a=8$ sind $g_a$ und $h_a$ identisch.

5.2

$g_a$ und $h_a$ sind orthogonal zueinander, wenn das Skallarprodukt ihrer Richtungsvektoren Null ergibt:

$a=-1$

Vollständige Lösung anzeigen

Bei $a=-1$ sind $g_a$ und $h_a$ orthogonal zueinander.

6.1

$\(\begin{array}[t]{rll} f(x)&=& \dfrac{1}{5}x^5+x^4-\dfrac{8}{3}x^3 \\[5pt] f$

Die lokale Änderungsrate beträgt an der Stelle $-11.$

6.2

Wende das notwendige Kriterium für Wendestellen an:

$x_1=0\quad x_2=1\quad x_3=-4$

Vollständige Lösung anzeigen

Die Wendestellen befinden sich bei $x_1=0,$ $x_2=1$ und $x_3=-4.$

7.1

Der Flächeninhalt lässt sich mit der Formel $A=\dfrac{1}{2}\cdot s_1\cdot s_2$ berechnen, da sich zwischen $\overline{OP}$ und $\overline{PQ}$ ein rechter Winkel befindet, weil $P$ und $Q$ den selben $x$ -Wert besitzen, wobei $s_1=a$ und $s_2=f(a)=a\cdot \mathrm e^{-a}$ .

7.2

Da das Maximum für den Flächeninhalt gesucht ist, berechnet man die Extrema des Terms $A(a).$

$a=2$

Vollständige Lösung anzeigen

Für $a=2$ ist der Flächeninhalt am größten.

8.1

$F(x)=\dfrac{1}{2}\cdot(x-2)^4+3$

$\(F$

Da $\(F$ gilt, ist $F$ eine Stammfunktion von $f_2.$

8.2

$F_1(x)=\dfrac{1}{4}(x-2)^4$

$F_{-1}(x)=-\dfrac{1}{4}(x-2)^4$

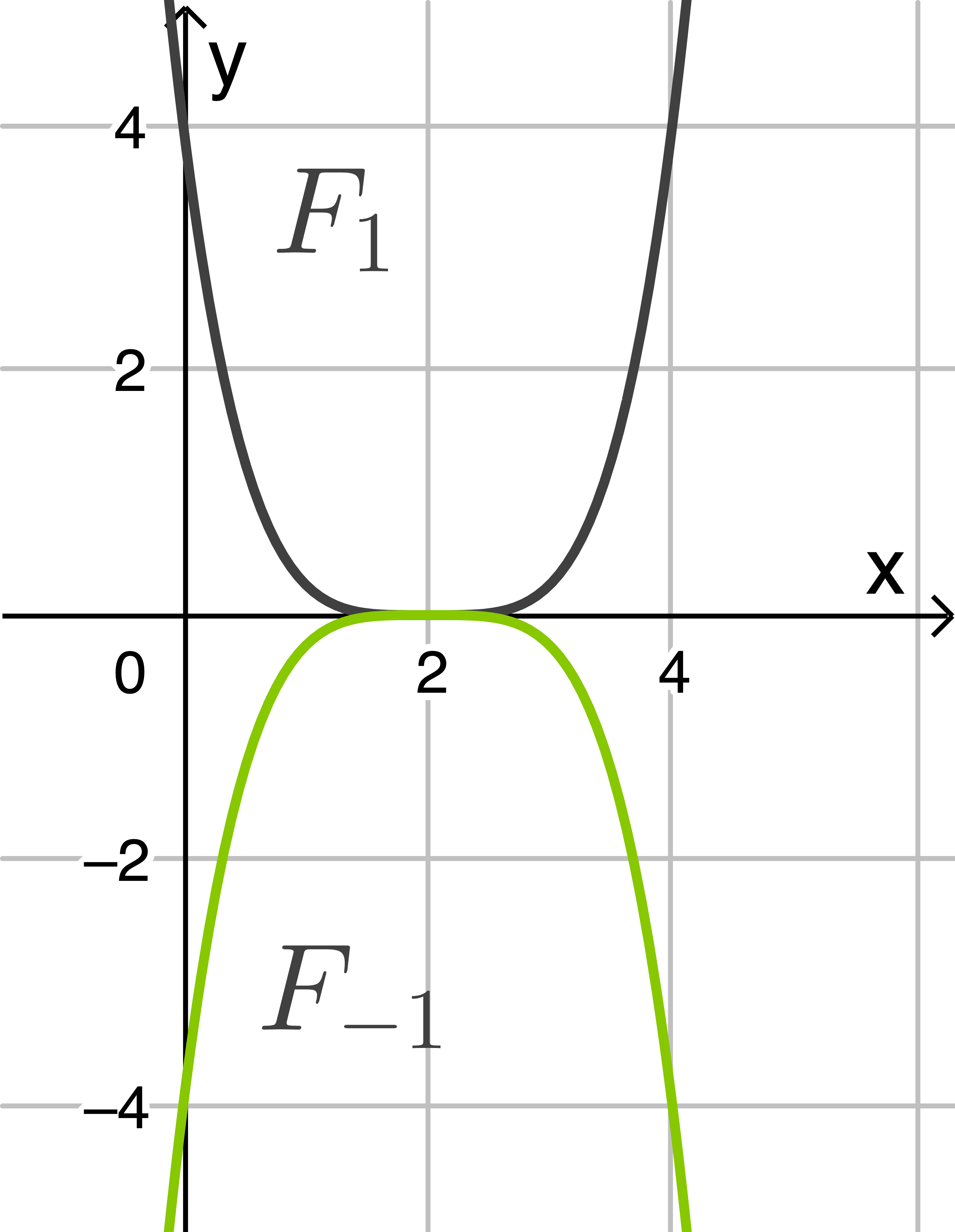
Grafik mit zwei Funktionen F₁ (schwarz) und F₋₁ (grün) im Koordinatensystem.

Die Terme aller Stammfunktionenvon $f_a$ lassen sich durch $F_{a,b}(x)=\frac{a}{4}\cdot(x-2)^4+b$ bin $b\in\mathbb{R}$ darstellen.
Für $a\gt0$ hat $F_{a,b}$ stets Funktionswerte, dienicht negativ sind (vgl. $F_1$ ).
Für $a\lt0$ gibt es stets Werte von $b,$ sodass $F_{a,b}$ nur negative Funktionswerte hat (vgl. $F_{-1}$ ).