Analysis 1
Aufgabe 1: Analysis
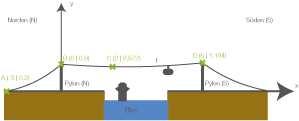
Vor einiger Zeit plante man in Hamburg eine von zwei Stützpfeilern (Pylonen) getragene Seilbahn über die Elbe. Die folgende Abbildung zeigt einen entsprechenden Entwurf. Dabei stellt die  -Achse den Verlauf der Erdbodenlinie dar. Eine Längeneinheit entspricht
-Achse den Verlauf der Erdbodenlinie dar. Eine Längeneinheit entspricht  in der Wirklichkeit.
in der Wirklichkeit.
Die Pylonenspitze  befindet sich
befindet sich  über dem Erdboden. Die Pylonenspitze
über dem Erdboden. Die Pylonenspitze  liegt
liegt  über dem Erdboden. Der Abstand der beiden Pylonen beträgt
über dem Erdboden. Der Abstand der beiden Pylonen beträgt  . Das nördliche Elbufer ist
. Das nördliche Elbufer ist  vom nördlichen Pylonen entfernt. Der Punkt
vom nördlichen Pylonen entfernt. Der Punkt  liegt senkrecht über dem nördlichen Elbufer. Die Seilhöhe beträgt hier
liegt senkrecht über dem nördlichen Elbufer. Die Seilhöhe beträgt hier  über dem Erdboden und die Steigung des Seiles im Punkt
über dem Erdboden und die Steigung des Seiles im Punkt  ist
ist  .
.
Bildnachweise [nach oben]
a)
Zwischen den Pylonen kann der Verlauf des Seiles näherungsweise durch eine ganzrationale Funktion  dritten Grades beschrieben werden.
dritten Grades beschrieben werden.
- Bestimme eine zugehörige Funktionsgleichung.
- Berechne im Bereich zwischen den Pylonen die minimale Höhe des Seiles über der Erdbodenlinie.
- Zu einem bestimmten Zeitpunkt befindet sich die Wasseroberfläche der Elbe
unter der Erdbodenlinie. Die Elbe ist im geplanten Bereich
breit. Berechne die durchschnittliche Höhe des Seiles über der Wasseroberfläche.
(17P)
b)
- Die Funktion
hat eine Wendestelle. Zeige, dass diese nicht im Intervall
liegt.
- Berechne die maximale Steigung des Graphen von
im Intervall
.
- Begründe, warum die Modellierung des Seiles durch einen Graphen mit einer Wendestelle
mit
nicht sinnvoll ist.
(8P)
c)
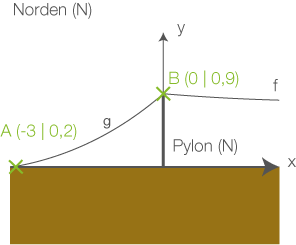
Die Station  auf dem Nordufer ist
auf dem Nordufer ist  vom nördlichen Pylonen entfernt. Das Seil befindet sich hier in einer Höhe von
vom nördlichen Pylonen entfernt. Das Seil befindet sich hier in einer Höhe von  über der Erdbodenlinie.
über der Erdbodenlinie.
Der Verlauf des Seils zwischen der Station und dem nördlichen Pylonen kann durch eine Funktion mit
mit  beschrieben werden.
beschrieben werden.
Der Verlauf des Seils zwischen der Station und dem nördlichen Pylonen kann durch eine Funktion
- Weise durch Rechnung nach, dass sich die beiden Koeffizienten
und
in der Form
- Berechne den Winkel, unter dem die Seile am nördlichen Pylonen aufeinandertreffen.
darstellen lassen.
(11P)
d)
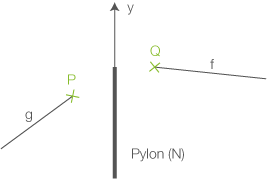
Um für die Fahrgäste ein angenehmes Fahren der Gondel zu ermöglichen, sollen knickfreie Übergänge hergestellt werden. Dazu hat der Konstrukteur die Punkte  und
und  auf den Graphen der zugehörigen Funktionen festgelegt und geplant, das Seil kreisbogenförmig vom Punkt
auf den Graphen der zugehörigen Funktionen festgelegt und geplant, das Seil kreisbogenförmig vom Punkt  zum Punkt
zum Punkt  zu führen.
zu führen.
Beschreibe ein Verfahren, mit dem untersucht werden kann, ob es einen solchen Kreisbogen gibt. Der Kreisbogen muss nicht durch den Punkt  verlaufen.
verlaufen.
(4P)
© 2016 - SchulLV.
© 2016 - SchulLV.
© 2016 - SchulLV.
a)
b)
c)
d)