Analytische Geometrie
Gegeben sind der Punkt  und die Gerade
und die Gerade
 mit
mit 
 und
und  liegen in der Ebene
liegen in der Ebene 
Ermittle eine Gleichung von in Koordinatenform.
[Zur Kontrolle:
in Koordinatenform.
[Zur Kontrolle:  ]
In der Abbildung ist neben
]
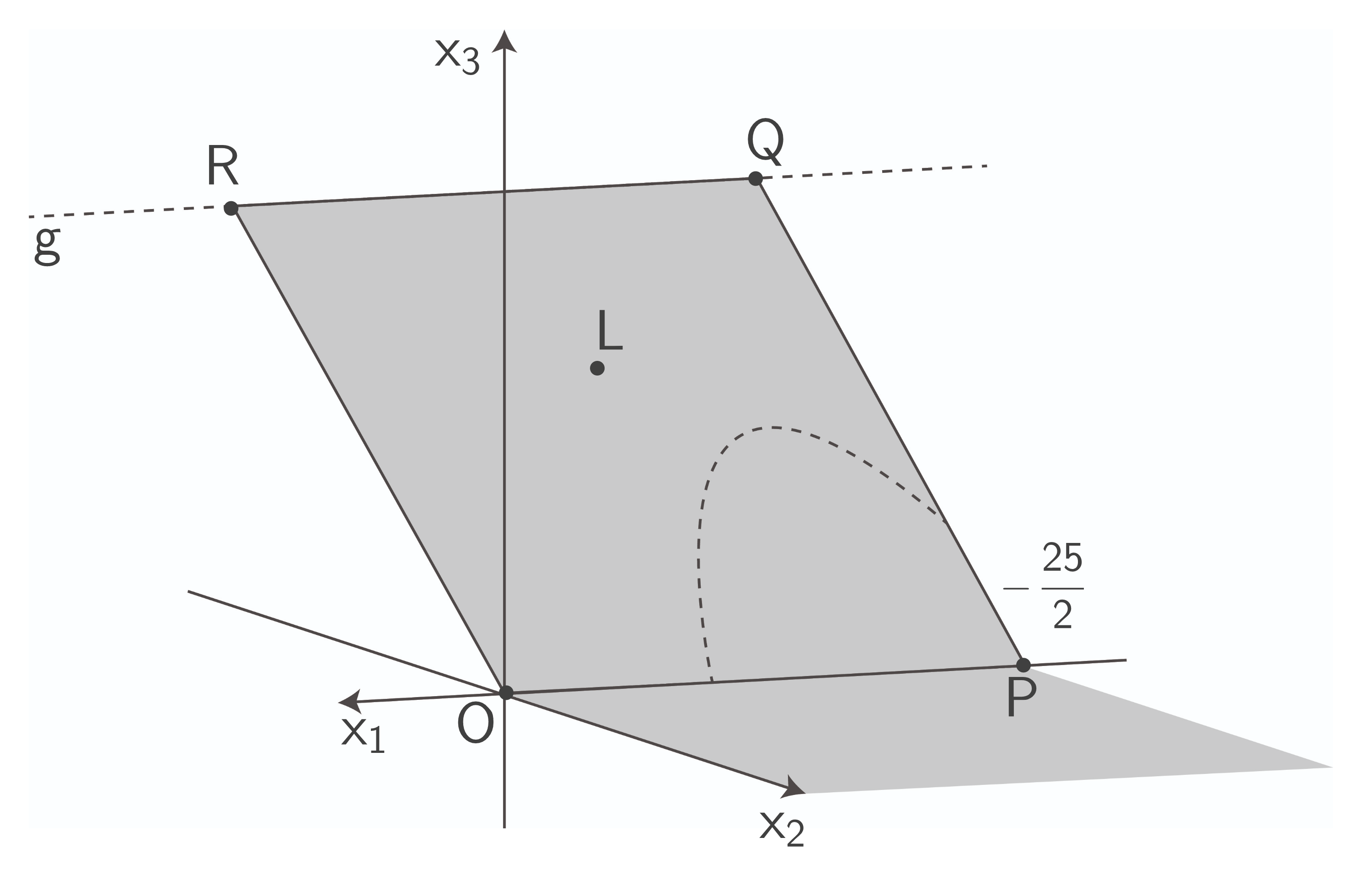
In der Abbildung ist neben  und
und  das Viereck
das Viereck  dargestellt, dessen Eckpunkte
dargestellt, dessen Eckpunkte 

 und
und  in
in  liegen.
liegen.  und
und  liegen außerdem auf
liegen außerdem auf 
 ist der Punkt in der Ebene
ist der Punkt in der Ebene  der durch Spiegelung des Punktes
der durch Spiegelung des Punktes  an der Geraden
an der Geraden  entsteht. Beschreibe ein Verfahren, mit dem man die Koordinaten des Punktes
entsteht. Beschreibe ein Verfahren, mit dem man die Koordinaten des Punktes  ermitteln könnte.
Das Viereck
ermitteln könnte.
Das Viereck  stellt modellhaft den geneigten Teil einer Minigolfbahn dar, der Punkt
stellt modellhaft den geneigten Teil einer Minigolfbahn dar, der Punkt  das Loch dieser Bahn. Im verwendeten Koordinatensystem beschreibt die
das Loch dieser Bahn. Im verwendeten Koordinatensystem beschreibt die  -Ebene den horizontalen Untergrund, eine Längeneinheit entspricht
-Ebene den horizontalen Untergrund, eine Längeneinheit entspricht  in der Realität.
in der Realität.
 befindet sich eine Lichtquelle.
befindet sich eine Lichtquelle.
a)
a1)
Begründe, dass  parallel zur
parallel zur  -Achse verläuft, aber nicht durch den Punkt
-Achse verläuft, aber nicht durch den Punkt 
(2 P)
a2)
Ermittle eine Gleichung von
(4 P)

b)
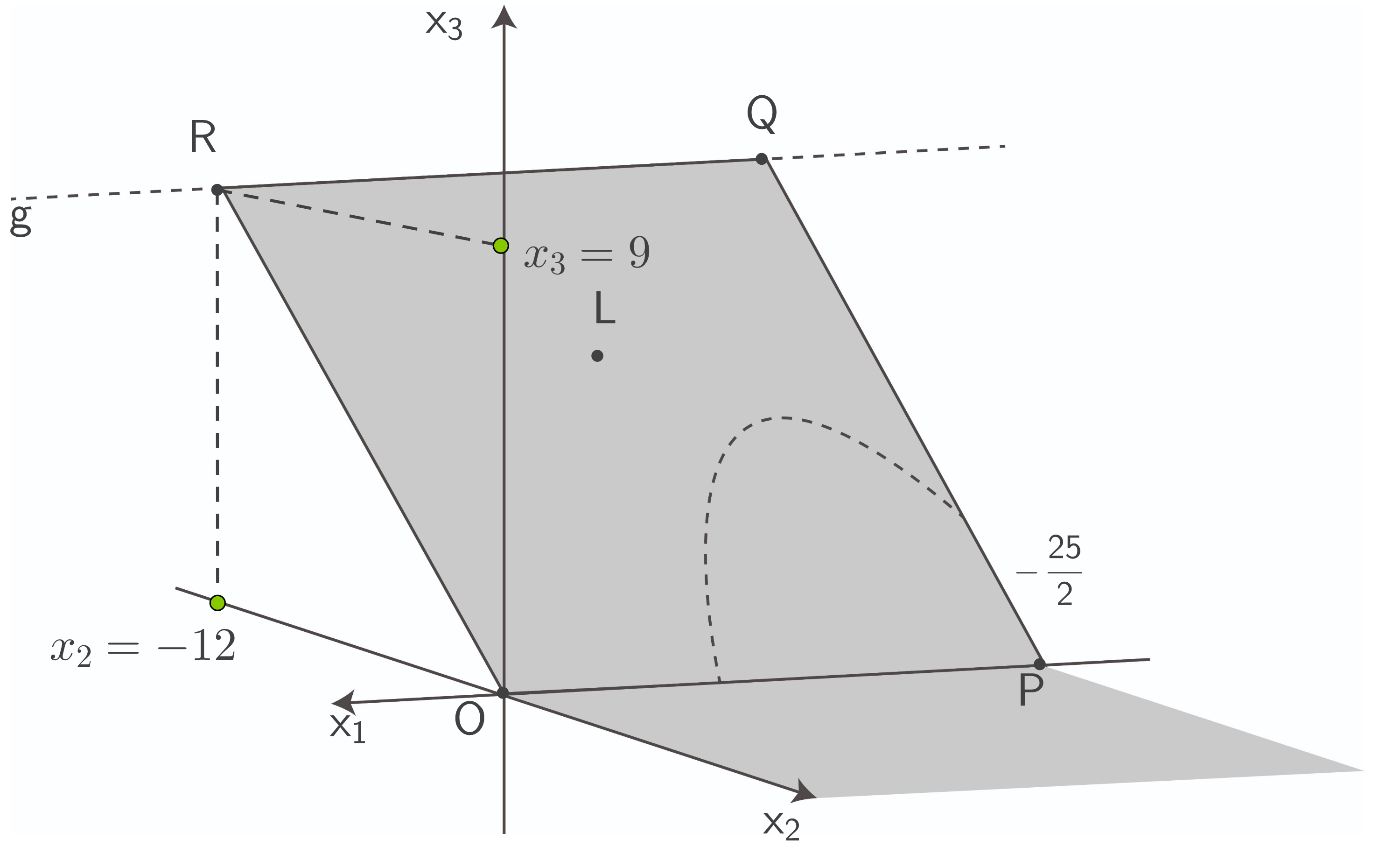
b1)
Markiere auf der  -Achse die Stelle
-Achse die Stelle  und auf der
und auf der  -Achse die Stelle
-Achse die Stelle 
(2 P)
b2)
Begründe, dass  ein Rechteck ist.
ein Rechteck ist.
Berechne den Flächeninhalt dieses Rechtecks.
Berechne den Flächeninhalt dieses Rechtecks.
(5 P)
b3)
Gib eine Gleichung der Geraden  an, die durch die Punkte
an, die durch die Punkte  und
und  verläuft.
verläuft.
(1 P)
b4)
(3 P)
c)
c1)
Berechne die Größe des Winkels, den der geneigte Teil der Bahn mit dem Untergrund einschließt.
Im Punkt
(3 P)
c2)
Berechne den Punkt  der Ebene
der Ebene  , der den kürzesten Abstand zur Beleuchtung
, der den kürzesten Abstand zur Beleuchtung  aufweist.
[Zur Kontrolle:
aufweist.
[Zur Kontrolle:  ]
]
(5 P)
c3)
Zeige, dass der Punkt  innerhalb des Vierecks
innerhalb des Vierecks  liegt.
liegt.
(3 P)
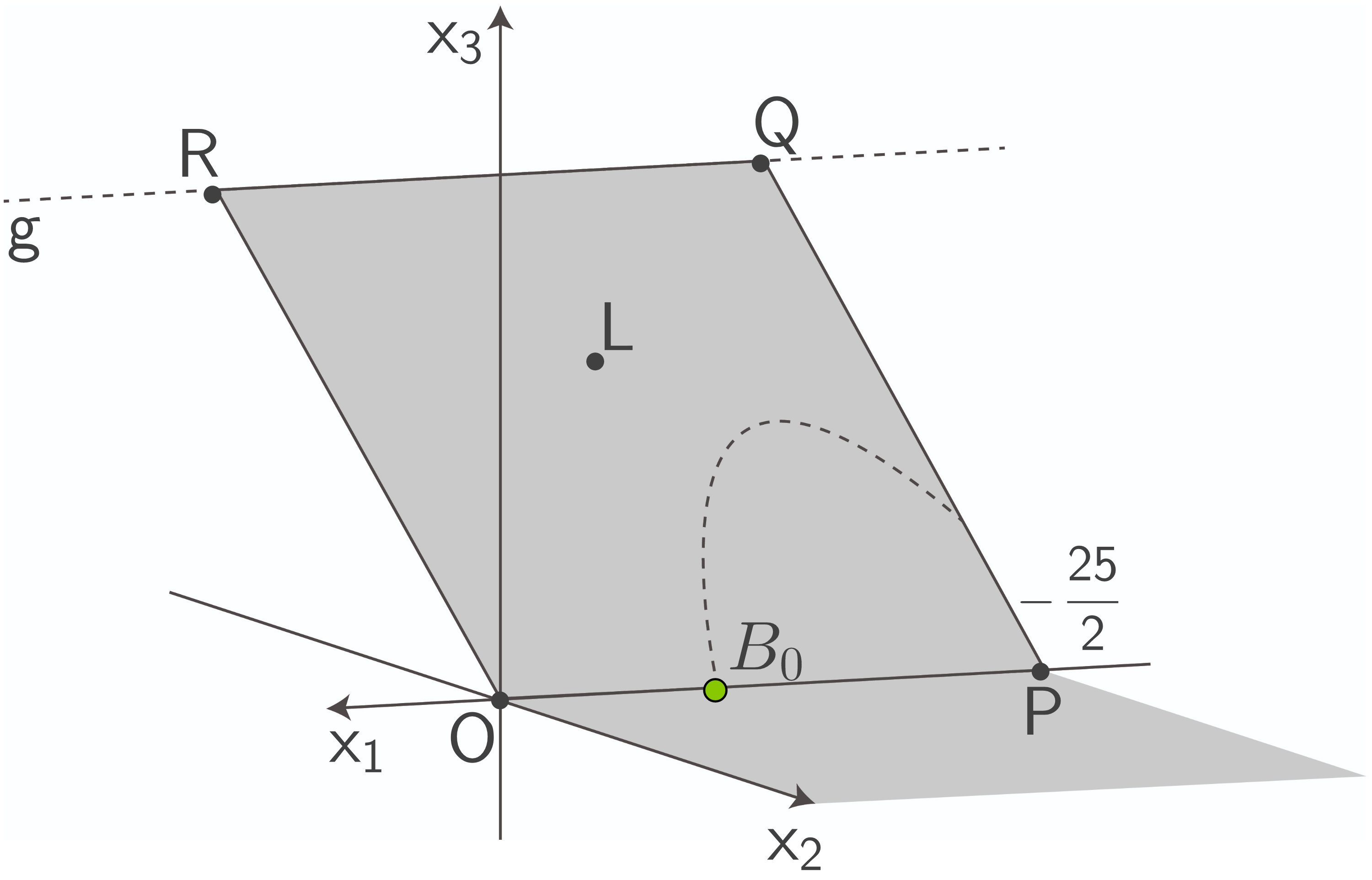
c4)
Der geneigte Teil der Bahn wirft durch die Beleuchtung einen viereckigen Schatten  auf den horizontalen Untergrund.
auf den horizontalen Untergrund.
Ermittle die Koordinaten des Eckpunktes
Ermittle die Koordinaten des Eckpunktes
(3 P)
d)
Im Folgenden wird der in der Abbildung gestrichelt dargestellte Teil des Weges eines Minigolfballs auf der Bahn betrachtet. Der Ball soll im Folgenden als punktförmig angenommen werden. Seine Positionen auf dem dargestellten Teil des Weges können durch Punkte
 mit geeigneten Werten
mit geeigneten Werten  beschrieben werden.
beschrieben werden.
d1)
Gib die Koordinaten des Punktes  an und zeichne den Punkt in die Abbildung ein.
an und zeichne den Punkt in die Abbildung ein.
(2 P)
d2)
Berechne im Modell die Koordinaten des Punktes, in dem der Weg des Balls auf die seitliche Begrenzung der Minigolfbahn trifft.
(4 P)
d3)
Ermittle die maximale Höhe über dem Untergrund, die der Ball erreicht, und gib diese Höhe in Zentimetern an.
(3 P)
a1)
a2)
b1)
b2)
Daraus lässt sich ableiten, dass alle Innenwinkel des Rechtecks
b3)
b4)
Man errechnet den orthogonalen Vektor von  indem man einen Vektor bestimmt, der als Skalarprodukt mit dem Richtungsvektor von
indem man einen Vektor bestimmt, der als Skalarprodukt mit dem Richtungsvektor von  Null ergibt.
Null ergibt.
Mit als Ortsvektor und
als Ortsvektor und  als Richtungsvektor lässt sich eine Geradengleichung für
als Richtungsvektor lässt sich eine Geradengleichung für  aufstellen.
aufstellen.
Nun wird der Schnittpunkt der beiden Geraden und
und  berechnet, indem man sie gleichsetzt.
berechnet, indem man sie gleichsetzt.
Der sich daraus ergebende Punkt ist der Punkt, an dem
ist der Punkt, an dem  gespiegelt wird.
gespiegelt wird.
Der Ortsvektor von wird berechnet, wenn man den Richtungsvektor
wird berechnet, wenn man den Richtungsvektor  mit zwei multipliziert. Durch Umformung in die Koordinatenform erhalten wir den Punkt
mit zwei multipliziert. Durch Umformung in die Koordinatenform erhalten wir den Punkt 
Mit
Nun wird der Schnittpunkt der beiden Geraden
Der sich daraus ergebende Punkt
Der Ortsvektor von
c1)
c2)
Der Punkt  liegt auf der Geraden, die senkrecht zu
liegt auf der Geraden, die senkrecht zu  durch den Punkt
durch den Punkt  verläuft. Ein möglicher Richtungsvektor dieser Geraden ist ein Normalenvektor von
verläuft. Ein möglicher Richtungsvektor dieser Geraden ist ein Normalenvektor von  Eine Gleichung dieser Geraden ist also beispielsweise:
Eine Gleichung dieser Geraden ist also beispielsweise:
 Der Schnittpunkt von
Der Schnittpunkt von  und
und  ist
ist  Für
Für  gilt:
gilt: 
 und
und  Setze dies in die Ebenengleichung von
Setze dies in die Ebenengleichung von  ein:
ein:
![\(\begin{array}[t]{rll}
3x_2 +4x_3 &=& 0 \\[5pt]
3\cdot (8+3u) + 4\cdot (24+ 4u) &=& 0 \\[5pt]
120 + 25u &=& 0 &\quad \scriptsize \mid\; -120 \\[5pt]
25u &=& -120 &\quad \scriptsize \mid\; :25 \\[5pt]
u &=& -4,8
\end{array}\)](https://mathjax.schullv.de/bde70b1467802abffceddd7105145dbf8fe276e4c62bdfb86b83ddb01ae47fce?color=5a5a5a)
 in
in  einsetzen:
einsetzen:


c3)
Der Ortsvektor von  lässt sich als Linearkombination der Vektoren darstellen, die das Viereck aufspannen, wobei die Parameter jeweils zwischen
lässt sich als Linearkombination der Vektoren darstellen, die das Viereck aufspannen, wobei die Parameter jeweils zwischen  und
und  liegen. Daher liegt der Punkt
liegen. Daher liegt der Punkt  innerhalb des Vierecks
innerhalb des Vierecks 
c4)
d1)
d2)
d3)
Die Funktion  wird abgeleitet und gleich Null gesetzt, so ermitteln wir die Extrema. Bei
wird abgeleitet und gleich Null gesetzt, so ermitteln wir die Extrema. Bei  ist der
ist der  Wert des Intervalls
Wert des Intervalls ![\([-5\leq x_1\leq-\frac{25}{2}]\)](https://mathjax.schullv.de/c9a12224385f181f00b50bd90324de6d944989091694b3d23abdb5792cbc99e3?color=5a5a5a) am größten.
am größten.


![\(\begin{array}[t]{rll}
f(t)&=& 0&\quad \scriptsize \\[5pt]
6-4t&=& 0 &\quad \scriptsize \mid\;-6\\[5pt]
-4t&=& -6 &\quad \scriptsize \mid\;:(-4)\\[5pt]
t&=& 1,5
\end{array}\)](https://mathjax.schullv.de/6dd467dc7ddf4b23c43d9965a430ae10654bd272810f27b95b701226cbae7924?color=5a5a5a)
 Die maximale Höhe beträgt
Die maximale Höhe beträgt  .
.