Analysis 1
Für den Beginn des Jahres 2020 modelliert der Graph der Funktion  mit
mit
 und
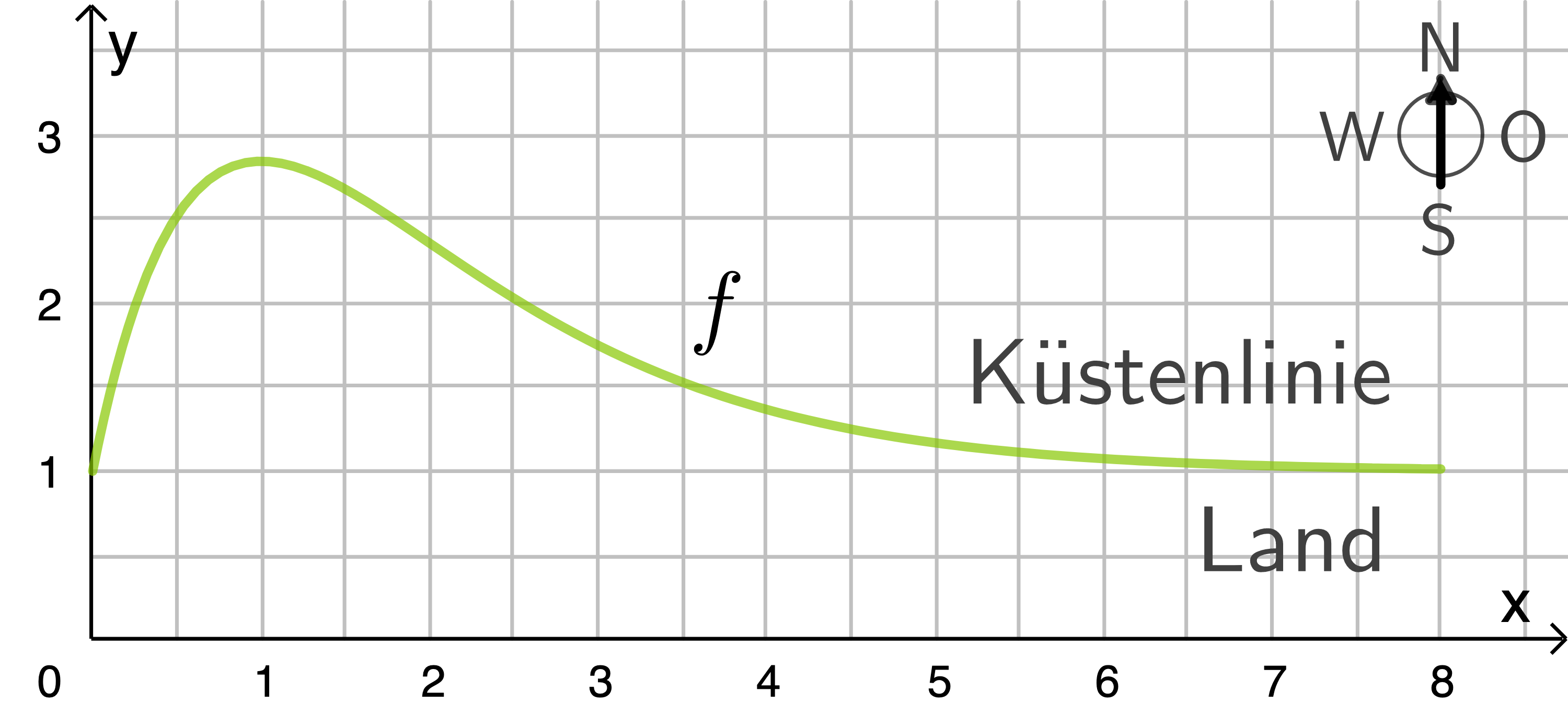
und ![\(x\in[0;8]\)](https://mathjax.schullv.de/516463ffda35d9fea7a740438e45a170c8fc87335d06663b2b9da5dca65b3004?color=5a5a5a) einen Teil einer Küstenlinie, die das Land vom Meer trennt. Die
einen Teil einer Küstenlinie, die das Land vom Meer trennt. Die  -Achse beschreibt eine Straße in West-Ost-Richtung. Die Fläche zwischen dem Graphen und der
-Achse beschreibt eine Straße in West-Ost-Richtung. Die Fläche zwischen dem Graphen und der  -Achse stellt das Land nördlich der Straße dar. Bei
-Achse stellt das Land nördlich der Straße dar. Bei  steht ein Leuchtturm.
steht ein Leuchtturm.
Eine Längeneinheit entspricht in der Wirklichkeit.
in der Wirklichkeit.
 Der betrachtete Teil der Küstenlinie wird sich im Laufe der Jahre verändern. In einem Rechenmodell wird der künftige Verlauf für
Der betrachtete Teil der Küstenlinie wird sich im Laufe der Jahre verändern. In einem Rechenmodell wird der künftige Verlauf für  durch die Funktion
durch die Funktion  mit
mit
 und
und ![\(x\in[0;8]\)](https://mathjax.schullv.de/516463ffda35d9fea7a740438e45a170c8fc87335d06663b2b9da5dca65b3004?color=5a5a5a) modelliert. Der Wert von
modelliert. Der Wert von  gibt an, wie viele Jahre seit Beginn des Jahres 2000 vergangen sind. Also entspricht
gibt an, wie viele Jahre seit Beginn des Jahres 2000 vergangen sind. Also entspricht  dem Beginn des Jahres 2020.
dem Beginn des Jahres 2020.
 hat der Graph der Funktion
hat der Graph der Funktion  einen Hochpunkt an der Stelle
einen Hochpunkt an der Stelle  Dieser Hochpunkt beschreibt den nördlichsten Punkt der jeweiligen Küstenlinie.
Dieser Hochpunkt beschreibt den nördlichsten Punkt der jeweiligen Küstenlinie.
Eine Längeneinheit entspricht

a)
a1)
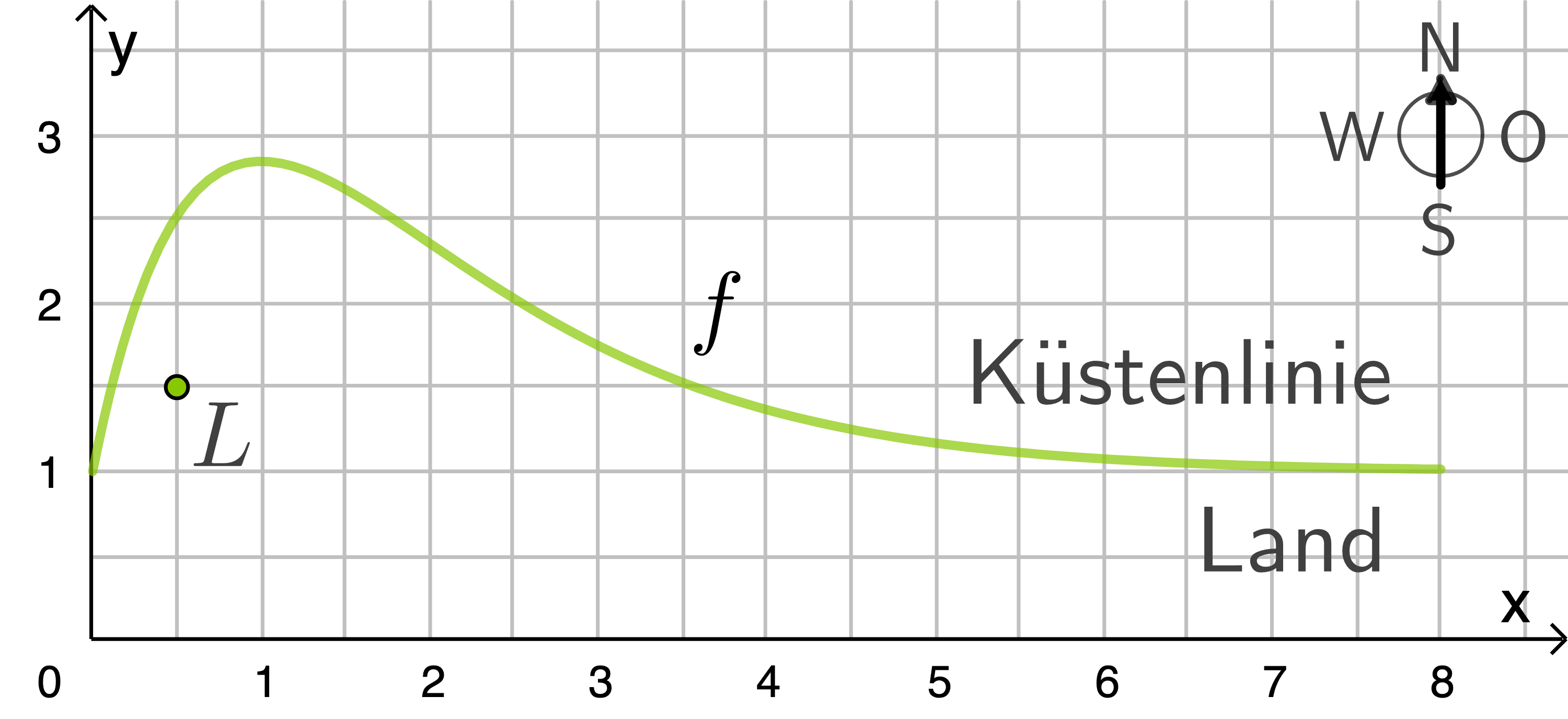
Zeichne den Punkt  in die Abbildung ein.
in die Abbildung ein.
Berechne die -Koordinate des Punkts der Küstenlinie an der Stelle
-Koordinate des Punkts der Küstenlinie an der Stelle 
Berechne die
(2 P)
a2)
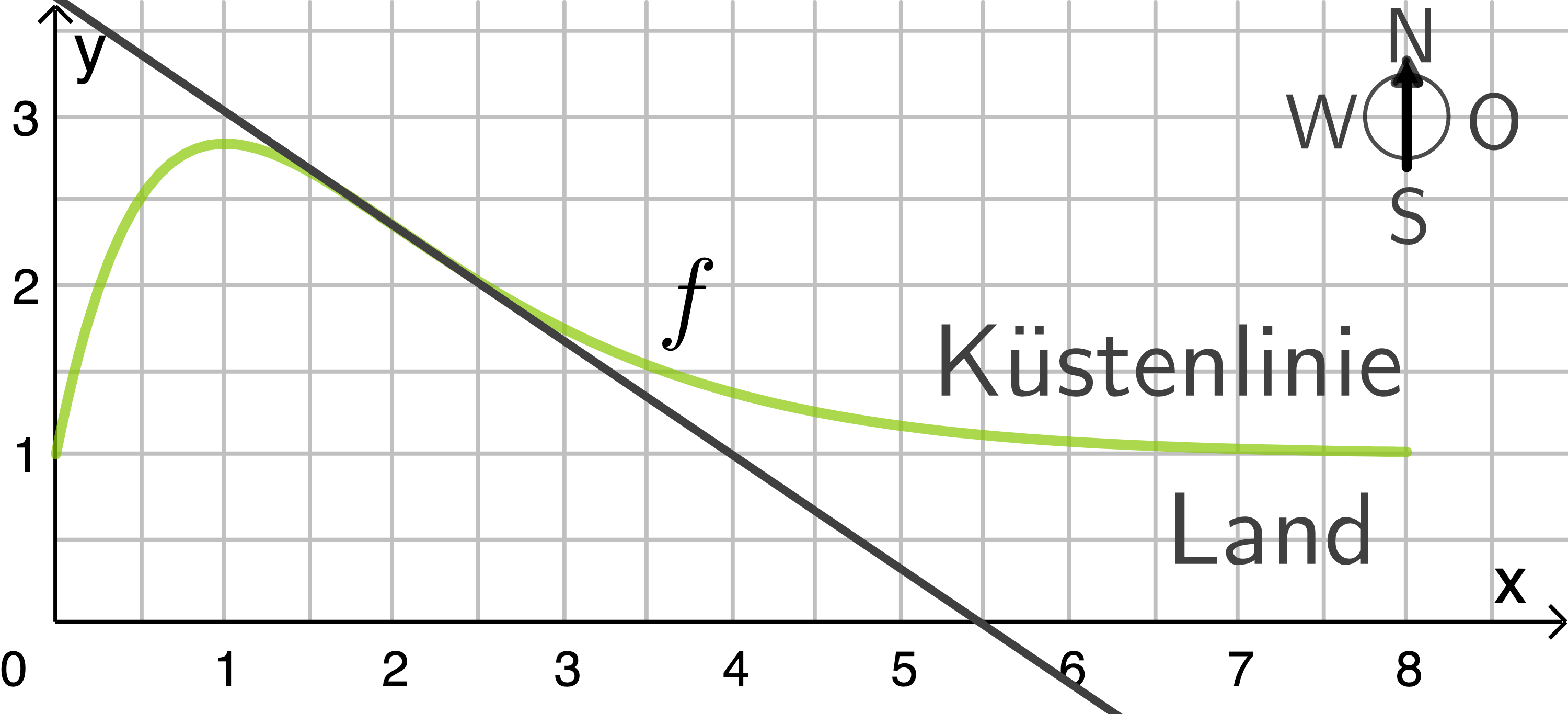
Zeichne die Tangente an den Graphen von  an der Stelle
an der Stelle  in die Abbildung ein, und bestimme deren Steigung.
in die Abbildung ein, und bestimme deren Steigung.
(2 P)
a3)
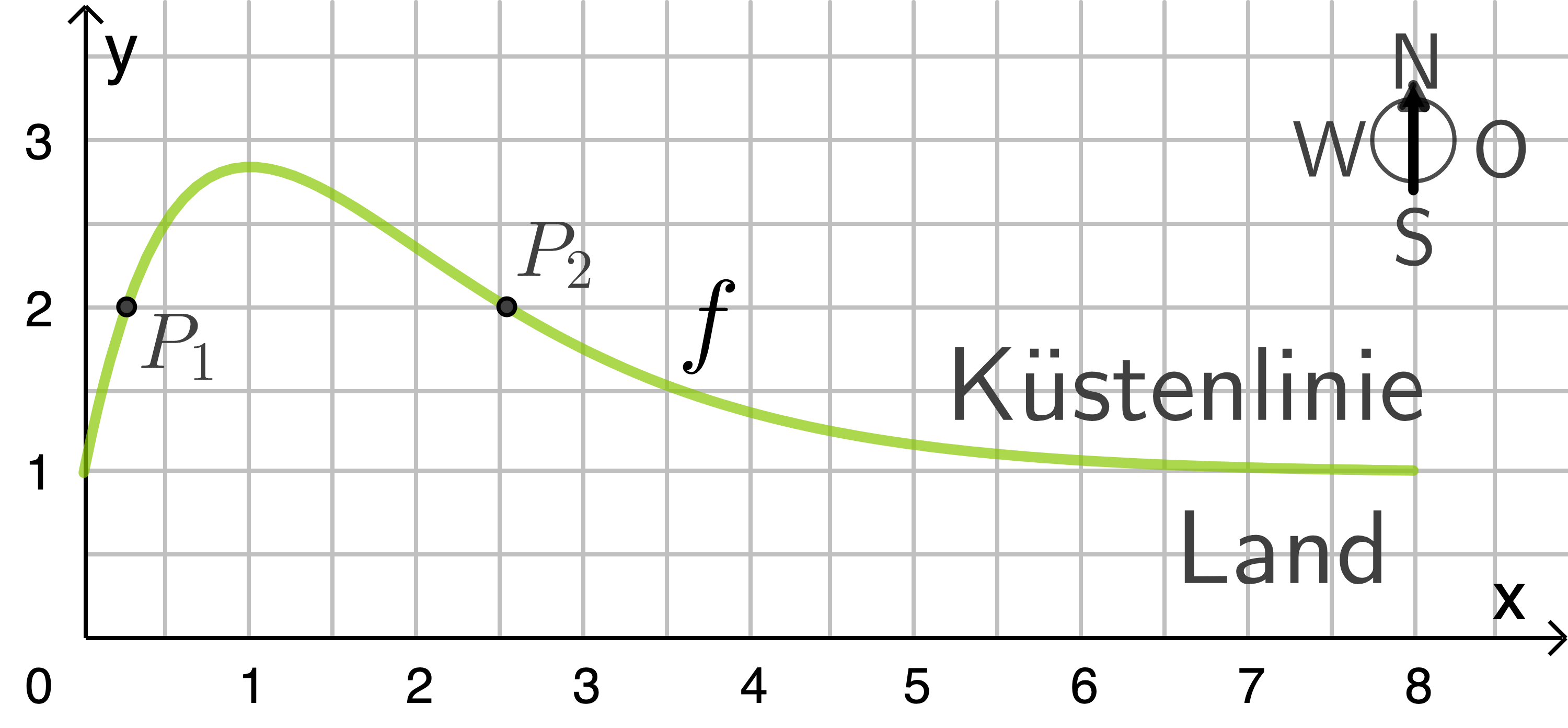
Es gibt auf dem betrachteten Teil der Küstenlinie Punkte, deren Abstand von der Straße  Meter beträgt.
Meter beträgt.
Zeichne die entsprechenden Punkte in die Abbildung ein.
Berechne die Koordinaten dieser Punkte.
Zeichne die entsprechenden Punkte in die Abbildung ein.
Berechne die Koordinaten dieser Punkte.
(3 P)
b)
b1)
Berechne die Kordinaten des nördlichsten Punkts auf dem betrachteten Teil der Küstenlinie.
[Zur Kontrolle:  ]
]
(5 P)
b2)
Bestimme alle Stellen ![\(x\in[0;8],\)](https://mathjax.schullv.de/304ebe3bbf9709d7a4ace56f25199febb35a2b42e8a8690daf5aec8b326a2cbf?color=5a5a5a) für die
für die  gilt.
gilt.
(3 P)
b3)
Berechne den mittleren Abstand der Punkte des betrachteten Teils der Küstenlinie zur Straße in Metern.
(3 P)
b4)
Bestimme mittels Integration einen Funktionsterm für eine Stammfunktion  von
von  .
.
(4 P)
c)
c1)
Berechne, in welchem Jahr der Leuchtturm auf der Küstenlinie stehen wird.
Für jedes
(3 P)
c2)
Bestimme eine Gleichung der Ortskurve, auf der die Hochpunkte liegen.
(3 P)
c3)
Vom Leuchtturm aus führt ein Weg genau in Nordrichtung. Zu einem bestimmten Zeitpunkt endet dieser Weg am nördlichsten Punkt der Küstenlinie.
Bestimme die Länge des Weges zu diesem Zeitpunkt.
Bestimme die Länge des Weges zu diesem Zeitpunkt.
(3 P)
d)
d1)
Berechne den Inhalt der Landfläche zwischen der Küstenlinie und der Straße im Intervall ![\([0;8]\)](https://mathjax.schullv.de/f865209a1807ce5fbc790d415dc19a6fa37135ca31f3a6fa1f42441652d095e7?color=5a5a5a) zu Beginn des Jahres 2150.
zu Beginn des Jahres 2150.
Begründe, dass der Inhalt der Landfläche auch in allen Jahren nach 2150 größer als Hektar sein wird.
Hektar sein wird.
Begründe, dass der Inhalt der Landfläche auch in allen Jahren nach 2150 größer als
(4 P)
d2)
Es gibt genau einen Wert  der die folgende Gleichung erfüllt:
Interpretiere die Bedeutung dieses Wertes
der die folgende Gleichung erfüllt:
Interpretiere die Bedeutung dieses Wertes  im Sachzusammenhang.
im Sachzusammenhang.
(2 P)
d3)
Bestimme alle reellen Zahlen  für die
für die  für
für  gilt.
gilt.
(3 P)
a1)
a2)
a3)
b1)
Es werden die Koordinaten des Hochpunktes des Graphen von  berechnet.
Wende die notwendige Bedingung für Extremstellen an.
berechnet.
Wende die notwendige Bedingung für Extremstellen an.

![\(\begin{array}[t]{rll}
0&=& 5\mathrm e^{-x}(1-x)&\quad \scriptsize \mid\;\mathrm e^{-x}\neq0 \\[5pt]
0&=& 1-x &\quad \scriptsize \mid\;+x \\[5pt]
x&=& 1
\end{array}\)](https://mathjax.schullv.de/36744ff27c9751aeafb29f99c6893615032efa811b1c568885dbb4e94489a30b?color=5a5a5a) Wende die hinreichende Bedingung für Extremstellen an.
Wende die hinreichende Bedingung für Extremstellen an.
 und
und 

![\(\begin{array}[t]{rll}
f](https://mathjax.schullv.de/58e2f05bf84e8abbe8adc5db25c63a170fffdc27bc31f1a299ff3c38bef36ce8?color=5a5a5a) An der Stelle
An der Stelle  besitzt der Graph von
besitzt der Graph von  einen Hochpunkt.
einen Hochpunkt.
 Der nördlichste Punkt liegt bei
Der nördlichste Punkt liegt bei 
b2)
b3)
Intervall ![\([0;8]\)](https://mathjax.schullv.de/f865209a1807ce5fbc790d415dc19a6fa37135ca31f3a6fa1f42441652d095e7?color=5a5a5a)
 Der mittlere Abstand der Punkte zur Straße beträgt
Der mittlere Abstand der Punkte zur Straße beträgt 
b4)
Mit der partiellen Integration wird eine Stammfunktion bestimmt:
c1)
c2)
Berechne die  -Koordinate der Hochpunkte.
-Koordinate der Hochpunkte.

 Forme die
Forme die  -Koordinate nach
-Koordinate nach  um:
um:
 Setze
Setze  in die
in die  -Koordinate ein. Damit ergibt sich die Gleichung der Ortskurve.
-Koordinate ein. Damit ergibt sich die Gleichung der Ortskurve.
![\(\begin{array}[t]{rll}
y&=& \frac{100}{a}\mathrm e^{-1}+1 \\[5pt]
&=&5\cdot\frac{20}{a}\mathrm e^{-1}+1&\quad\scriptsize\mid\;\frac{20}{a}=x \\[5pt]
&=& 5\mathrm e^{-1}\cdot x+1
\end{array}\)](https://mathjax.schullv.de/2862647079198d82bb34fb20819d1970081c0d3f90e21e8fe904128b676236ce?color=5a5a5a)
c3)
d1)
d2)
Zum Zeitpunkt  ist die Landfläche um
ist die Landfläche um  ihrer Ausgangsgröße geschrumpft, was sich aus dem Faktor
ihrer Ausgangsgröße geschrumpft, was sich aus dem Faktor  herleiten lässt, da dieser
herleiten lässt, da dieser  ersetzt.
ersetzt.
d3)
Wegen  gilt:
gilt:
![\(\begin{array}[t]{lrll}
&f_a(x)&\lt&f(x) \\[5pt]
\Leftrightarrow&5x\cdot\mathrm e^{-0,05a\cdot x}(x)&\lt&5x\cdot\mathrm e^{-x} \\[5pt]
\Leftrightarrow&\mathrm e^{-0,05a\cdot x}&\lt&e^{-x} \\[5pt]
\Leftrightarrow&-0,05a\cdot x&\lt&-x \\[5pt]
\Leftrightarrow&0,05a&\gt&1 \\[5pt]
\Leftrightarrow&a&\gt&20 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/fbaddca5aa7fa172afb94b712653fd6e54addde482d0ebe3757ed36a08a8534d?color=5a5a5a)