Analysis 1

Die folgende Abbildung zeigt den Längsschnitt durch das Modell eines Blauwals. Eine Längeneinheit beträgt $1$ Meter in der Wirklichkeit.

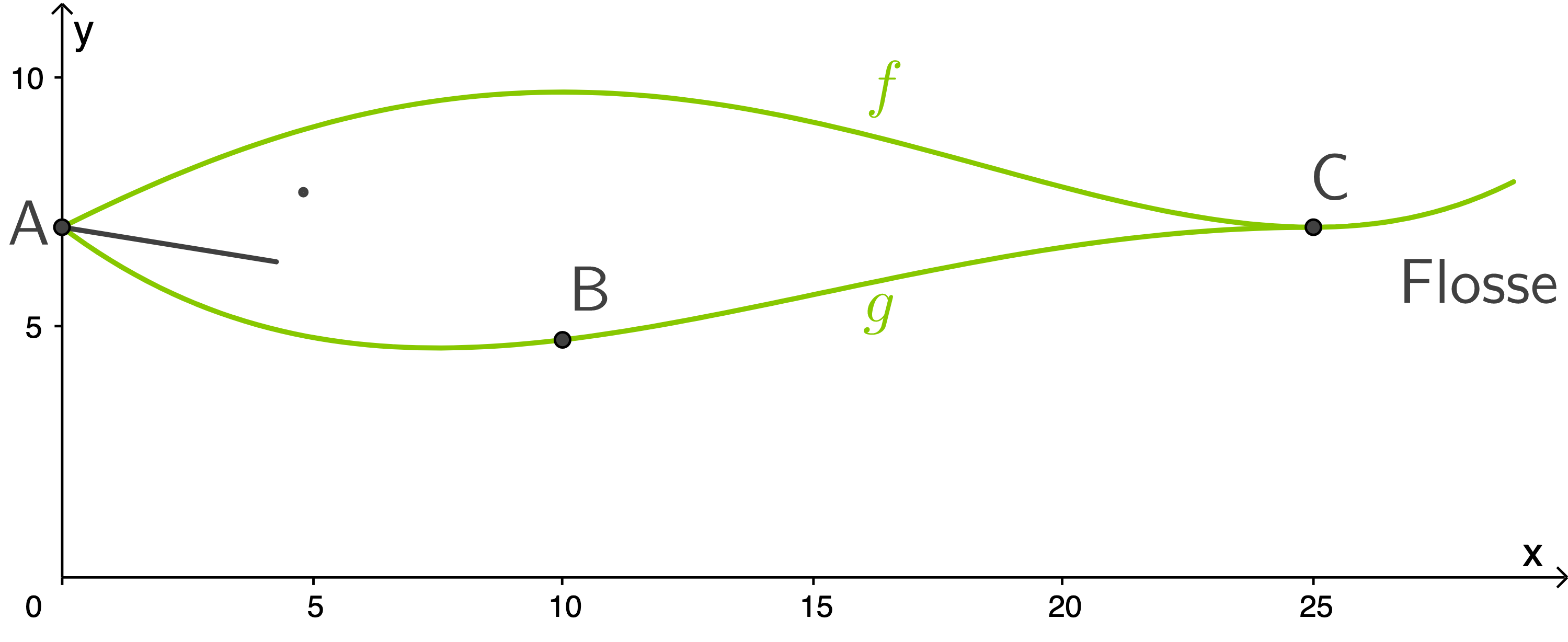Diagramm mit Kurven und Punkten A, B, C sowie Bezeichnungen f, g und Flosse. Achsen x und y sind beschriftet.

Die obere Begrenzung inklusive Flosse wird durch den Graphen der Funktion $f$ mit

Vollständige Funktion anzeigen

$f(x)= ...$

im Intervall $[0;29]$ beschrieben.
Die untere Begrenzung wird im Intervall $[0;25]$ durch den Graphen einer ganzrationalen Funktion $g$ vierten Grades modelliert. Der Graph von $g$ verläuft durch die Punkte $A(0\mid7),$ $B(10\mid\frac{19}{4})$ und $C(25\mid7).$ Seine Tangente an der Stelle $x=7,5$ ist waagerecht. Im Punkt $C$ erfolgt ein knickfreier Anschluss an den Graphen von $f.$

a1)

Bestimme einen Funktionsterm von $g.$

Vollständige Funktion anzeigen

[Zur Kontrolle: $g(x)= ...$

(7 P)

a2)

Für jedes $x$ aus dem Intervall $[0;25]$ wird die Dicke des Längsschnitts durch die Differenz der Funktionswerte von $f$ und $g$ an dieser Stelle $x$ beschrieben.
Berechne die maximale Dicke des Längsschnitts.

(6 P)

Ein Blauwal ist bei der Geburt $6\,\ \text{m}$ lang. Seine Wachstumsrate wird modelliert durch die Funktion $w$ mit

$w(x)=\dfrac{120\cdot\mathrm e^{0,9\cdot(x-5)}}{(\mathrm e^{0,9\cdot(x-5)}+6)^2}.$

Dabei steht $x$ für die Zeit in Jahren seit der Geburt und $w(x)$ für den Längenzuwachs in Meter pro Jahr.

b1)

Ermittle die Körperlänge des Blauwals nach acht Jahren.

(2 P)

b2)

Zeige, dass ein Blauwal, dessen Wachstumsrate durch die Funktion $w$ modelliert wird, immer weiter wachsen würde, aber eine Körperlänge von $29\,\text{m}$ nie erreichen könnte.

(4 P)

b3)

Ein Blauwahl ist nach dem Modell ausgewachsen, wenn er eine Körperlänge von $27,6\,\text{m}$ erreicht hat.
Bestimme das Alter, ab dem der Blauwal ausgewachsen ist.

(3 P)

Die Funktion $w$ ist in der Schar $w_k$ mit

$w_k(x)=\dfrac{120\cdot\mathrm e^{k\cdot(x-5)}}{(\mathrm e^{k\cdot(x-5)}+6)^2}$

mit $k\gt0$ enthalten.
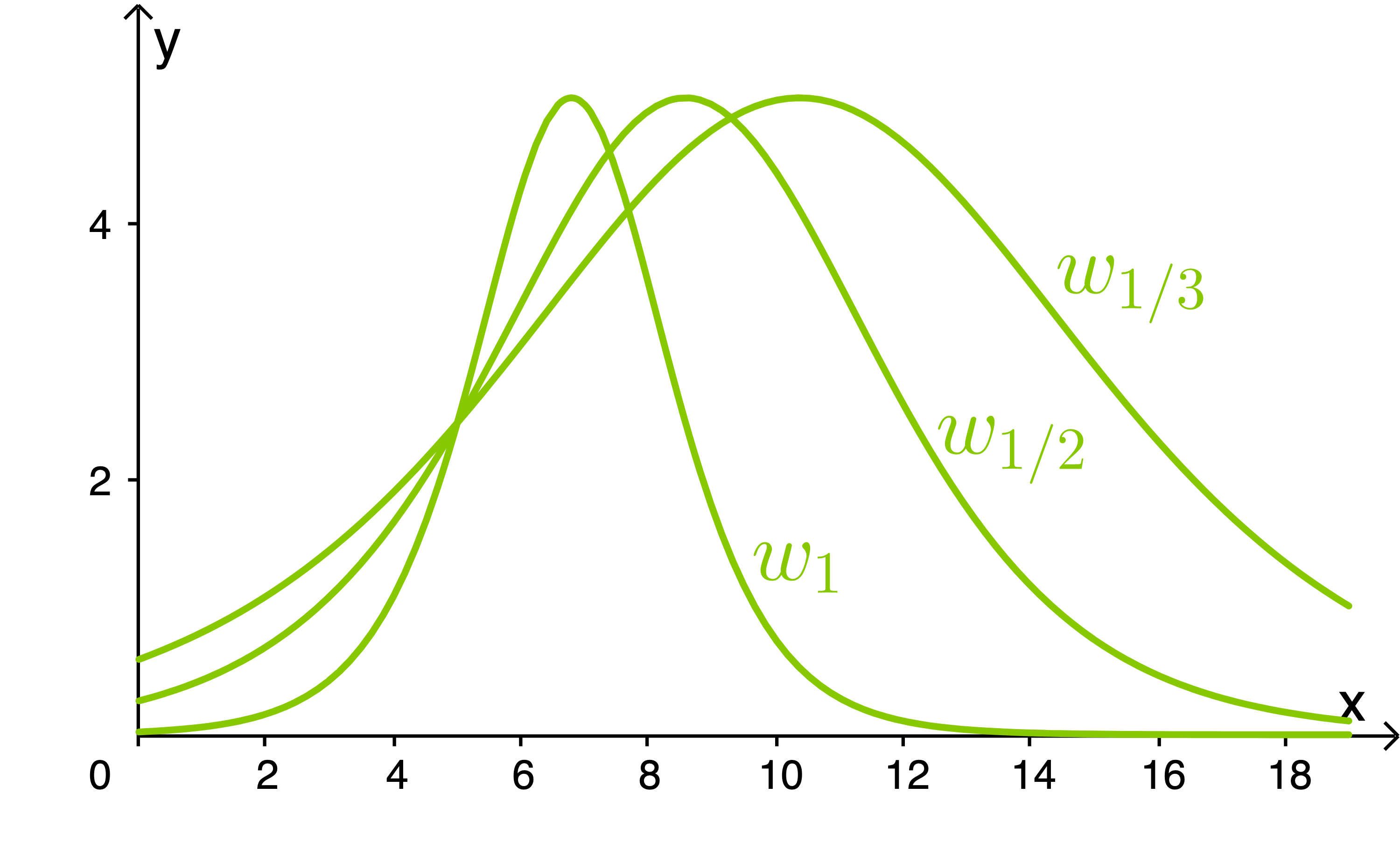
Die Abbildung zeigt die Graphen von $w_1,$ $w_{\frac{1}{2}}$ und $w_{\frac{1}{3}}.$

Diagramm mit grünen Kurven, die eine Funktion im Koordinatensystem darstellen. Achsen beschriftet mit x und y.

c1)

Beschreibe anhand der dargestellten Graphen den Einfluss des Parameters $k$ auf die Koordinaten des Hochpunktes und auf den $y-$ Achsenabschnitt.

(3 P)

c2)

Zeige, dass der Punkt $P\left(5\mid\frac{120}{49}\right)$ für alle $k\gt0$ auf dem Graphen von $w_k$ liegt.
Weise nach, dass $P$ für kein $k\gt0$ ein Wendepunkt sein kann.

(5 P)

c3)

Zeige rechnerisch, dass alle Hochpunkte der Graphen von $w_k$ auf einer Geraden liegen.
Bestimme einen Wert für $k,$ so dass $w_k$ an der Stelle $x=6$ ein lokales Maximum annimmt.

(6 P)

c4)

Jeder Graph der Funktionenschar $w_k$ ist symmetrisch zu einer Parallelen zur $y-$ Achse durch den Punkt $Q_k\left(5+\frac{\ln(6)}{k}\mid0\right).$ Der Punkt $P\left(5\mid\frac{120}{49}\right)$ besitzt somit auf jedem Funktionsgraphen einen Spiegelpunkt $\(P$ Die Punkte $P,$ $Q_k$ und $\(P$ bilden die Eckpunkte eines Dreiecks.
Bestimme den Parameter $k$ so, dass der Flächeninhalt des Dreiecks genau $1$ beträgt.

(4 P)

a1)

$g(x)=ax^4+bx^3+cx^2+dx+e$

$\(g$

Gegeben ist $\(g(0)=7, \,\ g(10)=\frac{19}{4}, \,\ g(25)=7, \,\ g$ und $\(g$

Gleichungssystem kann im Taschenrechner gelöst werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 3: Algebra $\to$ 7

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math1 $\to$ $\{^{\Box}_{\Box}$

$a=\frac{1}{50000}, \quad b=-\frac{11}{5000}, \quad c=\frac{29}{400}, \quad d=-\frac{3}{4}$ und $e=7$

$g(x)=\dfrac{1}{50000}x^4-\dfrac{11}{5000}x^3+\dfrac{29}{400}x^2-\dfrac{3}{4}x+7$

a2)

Gesucht ist das globale Maximum der Funktion $d$ mit $d(x)=f(x)-g(x)$ im Intervall $[0;25].$
Die notwendige Bedingung, für ein lokales Maximum von $d$ an der Stelle $x,$ ist $\(d$
Mit dem Solve-Befehl des CAS folgt: $\(d$
(Der Wert $x\approx-71,3$ entfällt als Lösung, da er nicht im betrachteten Intervall liegt.)
Die Dicke der Ränder des Intervalls ist null.
Da zusätzlich $d(8,77)\approx5,03\gt0$ gilt, ist die hinreichende Bedingung für ein globales Maximum an der Stelle $x\approx8,77$ erfüllt.
Die maximale Dicke des Längsschnitts beträgt somit ca. $5,03\,\ \text{m}.$

b1)

Zur Ausgangsgröße des Wals wird der Längenzuwachs der $8$ Jahre addiert. Verwende deinen CAS:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$6+\displaystyle\int_{0}^{8}w(x) \;\mathrm dx=\displaystyle\int_{0}^{8}\dfrac{120\cdot\mathrm e^{0,9\cdot(x-5)}}{(\mathrm e^{0,9\cdot(x-5)}+6)^2} \mathrm dx\approx21,80$

Der Wal ist nach $8$ Jahren ca. $21,8\,\ \text{m}$ lang.

b2)

Da $x\gt0$ ist gilt $120\cdot\mathrm e^{0,9\cdot(x-5)}\gt0$ und $(\mathrm e^{0,9\cdot(x-5)}+6)^2\gt0$ , wodurch $w(x)\gt0$ ist. Das Wachstum wird zwar geringer, doch hört nie auf.
$6+\lim\limits_{b\to\infty}\displaystyle\int_{0}^{b}w(x)\; \mathrm dx\approx28,18\quad,$
Somit wird der Wal nie $29\,\ \text{m}$ oder länger sein.

b3)

$6+\displaystyle\int_{0}^{b}w(x) \;\mathrm dx=27,6$

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 3: Integral

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\int_{\Box}^{\Box}\Box$

$b\approx11,01$
Der Wal ist zu Beginn seines elften Lebensjahres ausgewachsen.

c1)

Je größer $k$ wird, desto kleiner wird die $x-$ Koordinate des Hochpunktes und der $y-$ Achsenabschnitt. Die $y$ -Koordinate des Hochpunktes scheint unabhängig von $k$ zu sein.

c2)

$w_k(5)=\dfrac{120\cdot\mathrm e^{k\cdot(5-5)}}{(\mathrm e^{k\cdot(5-5)}+6)^2}$ $=\dfrac{120}{7^2}=\dfrac{120}{49}$

Somit liegt $P$ auf allen Graphen der Funktionsschar mit $k\gt0.$

Wäre $P$ ein Wendepunkt von allen Graphen von $w_k\,\ (k\gt0),$ müsste $\(w$ sein. Also muss die zweite Ableitung von $w_k$ gebildet werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

$\(w$

Da $k\gt0$ ist, gilt auch für $\(w$ Dadurch ist $P$ nie ein Wendepunkt eines Graphen der Funktionsschar.

c3)

Als notwendige Bedingung für einen Hochpunkt muss $\(w$ gesetzt werden:

$\blacktriangleright$ TI nspire CAS

menu $\to$ 4: Analysis $\to$ 1: Ableitung

$\blacktriangleright$ Casio Classpad II

keyboard $\to$ Math2 $\to$ $\frac{d}{d \Box}\Box$

Für jedes $k\gt0$ liegt wegen $\(w$ und $\(w$ an der Stelle $x=\dfrac{5k+\ln(6)}{k}$ ein lokales Maximum von $w_k$ vor.

$w_k\left(\dfrac{5k+\ln(6)}{k}\right)=5$ damit sind die Koordinaten aller Hochpunkte von $w_k$ in $H_k\left(\dfrac{5k+\ln(6)}{k}\mid5\right)$ enthalten.

Da alle Hochpunkte den selben $y-$ Wert besitzen, hat die Gerade, die sie schneidet, die Gleichung $y=5.$

$\begin{array}[t]{rll} 6&=& \dfrac{5k+\ln(6)}{k} &\quad \scriptsize \mid\;\cdot k \\[5pt] 6k&=& 5k+\ln(6) &\quad \scriptsize \mid\;-5k \\[5pt] k&=& \ln(6)\end{array}$

$w_{\ln(6)}(x)$ besitzt bei $x=6$ ein lokale Maximum.

c4)

Grafische Darstellung einer mathematischen Funktion mit einem Scheitelpunkt und Achsen.

Der Abstand der $x$ -Koordinaten von $P(5\mid\frac{120}{49})$ und $Q_k(5+\frac{\ln(6)}{k}\mid0)$ beträgt $\frac{\ln(6)}{k}$ . Dadurch hat $\(\overline{PP$ eine Länge von $2\cdot\frac{\ln(6)}{k}$ und bildet die Grundseite des Dreiecks. Die Höhe beträgt $\frac{120}{49}.$ Der Flächeninhalt kann also wie folgt berechnet werden

$A(k)=\dfrac{1}{2}\cdot2\cdot\dfrac{\ln(6)}{k}\cdot\dfrac{120}{49}$ $=\dfrac{\ln(6)}{k}\cdot\dfrac{120}{49}$

Für $A(k)=1$ gilt $k=\frac{120}{49}\cdot \ln(6)\approx4,39.$

Das Dreieck $\(PQ_{4,39}P$ besitzt den Flächeninhalt $1.$