Aufgabe 3: Stochastik

3.1

Bei einer statistischen Erhebung werden in einer deutschen Großstadt die privaten Haushalte mit mindestens einem Kind im Vorschulalter betrachtet. Diese werden im Folgenden als „junge Haushalte“ bezeichnet.

Es wird festgestellt, dass $60 \,\%$ der jungen Haushalte mit mindestens einem Pkw ausgestattet sind und $8\,\%$ der jungen Haushalte mit mindestens einem Lastenrad. In $14 \,\%$ der jungen Haushalte ohne Pkw ist mindestens ein Lastenrad vorhanden.

Stelle den beschriebenen Sachverhalt in einer vollständig ausgefüllten Vierfeldertafel dar.

(4 BE)

Beurteile für diese Großstadt die folgende Aussage:

Die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter junger Haushalt mit mindestens einem Lastenrad ausgestattet ist, ist bei einem jungen Haushalt ohne Pkw mehr als dreimal so groß wie bei einem jungen Haushalt mit mindestens einem Pkw.

(3 BE)

Begründe, dass weniger als $68\,\%$ der jungen Haushalte mit mindestens einem Pkw oder mit mindestens einem Lastenrad ausgestattet sind.

(2 BE)

300 junge Haushalte dieser Großstadt werden zufällig ausgewählt.

Bestimme die Wahrscheinlichkeit dafür, dass mehr als 20 und höchstens 30 dieser Haushalte mit mindestens einem Lastenrad ausgestattet sind.

(3 BE)

Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term $1-\displaystyle\sum\limits_{k=201}^{300}\pmatrix{300\\k}\cdot 0,6^k\cdot 0,4^{300-k}$ berechnet werden kann.

(2 BE)

3.2

Betrachtet werden Vorderrad- und Hinterradreifen für Lastenräder. Auf einem Prüfstand kann die Laufleistung von solchen Reifen gemessen werden. Die Laufleistung gibt die auf dem Prüfstand ermittelte Gesamtstrecke an, bis der Reifen unbrauchbar wird.

Die Zufallsgröße $V$ beschreibt die Laufleistung in Kilometern ( $\,\text{km}$ ) der Vorderradreifen eines bestimmten Herstellers, die Zufallsgröße $H$ der Hinterradreifen desselben Herstellers.

$V$ wird als normalverteilt mit dem Erwartungswert $6800\,\text{km}$ und der Standardabweichung $530\,\text{km}$ angenommen.

$H$ wird als normalverteilt mit dem Erwartungswert $4600\,\text{km}$ und der Standardabweichung $480\,\text{km}$ angenommen.

Bestimme die Wahrscheinlichkeit dafür, dass ein zufällig ausgewählter Vorderradreifen dieses Herstellers eine Laufleistung hat, die um höchstens $600 \,\text{km}$ vom Erwartungswert für diese Laufleistung abweicht.

(3 BE)

Begründe, dass die folgende Aussage für die Vorderrad- und Hinterradreifen dieses Herstellers wahr ist:

Die Laufleistung, die ein zufällig ausgewählter Vorderradreifen gemäß dem Modell mit der Wahrscheinlichkeit von $90 \,\%$ übertreffen wird, wird ein zufällig ausgewählter Hinterradreifen nahezu mit Sicherheit unterschreiten.

(4 BE)

Die Zufallsgröße $Z$ beschreibt die Laufleistung in $\,\text{km}$ der Hinterradreifen eines anderen Herstellers. $Z$ wird als normalverteilt mit dem Erwartungswert $\mu_{Z}$ und der Standardabweichung $\sigma_{Z}$ angenommen.

Die Abbildung stellt den Graphen der Funktion $f$ mit $f(x)=P(Z \leq 1000 \cdot x)$ dar.

Ermittle die Werte von $\mu_{Z}$ und $\sigma_{Z}$ jeweils in $\,\text{km}.$

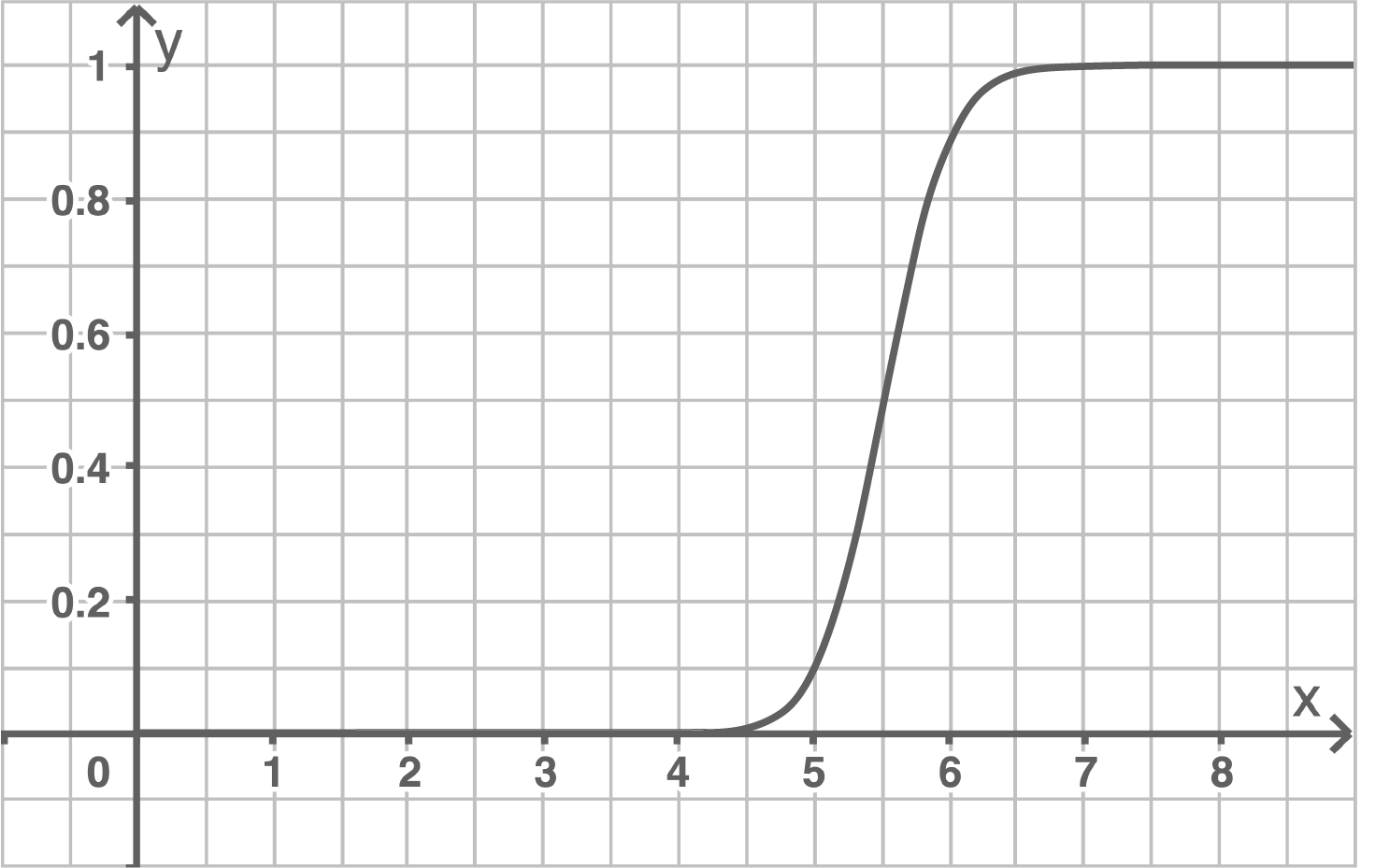
Zufallsgroesse Z Erwartungswert Mathe Abi 2024

(4 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

3.1

$P:$ Junger Haushalt besitzt mindestens einen Pkw

$L:$ Junger Haushalt besitzt mindestens ein Lastenrad

Da $14\,\%$ der jungen Haushalte ohne Pkw mindestens ein Lastenrad besitzen, gilt:

$\begin{array}[t]{rll} P(L \cap \overline{P})&=& 0,14\cdot 0,4& \\[5pt] &=& 0,056& \\[5pt] \end{array}$

Einsetzen der gegebenen Anteile und Aufsummieren zum jeweiligen Gesamtanteil liefert:

	$\color{#fff}{L}$	$\color{#fff}{\overline{L}}$	Gesamt
$\color{#fff}{P}$	$0,024$	$0,576$	$0,6$
$\color{#fff}{\overline{P}}$	$0,056$	$0,344$	$0,4$
Gesamt	$0,08$	$0,92$	$1$

Wahrscheinlichkeit, dass ein zufällig ausgewählter junger Haushalt ohne Pkw mindestens ein Lastenrad besitzt:

$\begin{array}[t]{rll} P(L \mid \overline{P})&=& \dfrac{P(\overline{P} \cap L)}{P(\overline{P})}&\\[5pt] &=& \dfrac{0,056}{0,4}&\\[5pt] &=& 0,14 \end{array}$

Wahrscheinlichkeit, dass ein zufällig ausgewählter junger Haushalt mit Pkw mindestens ein Lastenrad besitzt:

$\begin{array}[t]{rll} P(L \mid P)&=& \dfrac{P(P \cap L)}{P(P)}&\\[5pt] &=& \dfrac{0,024}{0,6}&\\[5pt] &=& 0,04 \end{array}$

Es gilt also $3\cdot P(L \mid P)=3\cdot 0,04=0,12$ und folglich $P(L \mid \overline{P}) \gt 3\cdot P(L \mid P).$

Die Aussage ist somit korrekt.

Der Ansatz $P(P)+P(L)=0,68$ zur Berechnung des Anteils genügt nicht, da die $2,4\,\%$ der jungen Haushalte, welche sowohl mindestens einen Pkw als auch mindestens ein Lastenrad besitzen, in der Wahrscheinlichkeit $P(P)$ sowie auch in der Wahrscheinlichkeit $P(L)$ inbegriffen sind.

Dieser doppelt gezählte Anteil muss folglich einmal von den $68\,\%$ abgezogen werden.

Der korrekte Anteil ergibt sich also zu:

$\begin{array}[t]{rll} P(P\cup L)&=& P(P)+P(L)-P(P\cap L)& \\[5pt] &=& 0,6+0,08-0,024 & \\[5pt] &=& 0,656 & \\[5pt] &=& 65,6\,\% \end{array}$

Die Zufallsvariable $X$ beschreibt die Anzahl der Haushalte, welche mit mindestens einem Lastenrad ausgestattet sind, und kann als binomialverteilt mit $n=300$ und $p=0,08$ angenommen werden.

Mit dem binomialcdf-Befehl des Taschenrechners ergibt sich:

$P(20 \lt X \leq 30) \approx 68,1\,\%$

Rechenweg anzeigen

Von 300 zufällig ausgewählten jungen Haushalten sind weniger als 201 Haushalte mit mindestens einem Pkw ausgestattet.

3.2

Für die Vorderradreifen gilt:

$\begin{array}[t]{rll} \mu_V-600 \,\text{km}&=& 6800 \,\text{km}-600\,\text{km} & \\[5pt] &=& 6200 \,\text{km} \end{array}$

$\begin{array}[t]{rll} \mu_V+600 \,\text{km}&=& 6800 \,\text{km}+600 \,\text{km} & \\[5pt] &=& 7400 \,\text{km} \end{array}$

Mit dem normalcdf-Befehl folgt:

$P(6200 \leq V \leq 7400)\approx 0,7424$

Durch systematisches Ausprobieren ergibt sich:

$\begin{array}[t]{rll} P(6120 \leq V)&\approx& 0,90026& \\[5pt] P(6121 \leq V)&\approx& 0,89993 \end{array}$

Gemäß dem Modell übertrifft ein zufällig ausgewählter Vorderradreifen des Herstellers somit zu $90\,\%$ eine Laufleistung von $6120\,\text{km}.$

Die Wahrscheinlichkeit, dass ein zufällig ausgewählter Hinterreifen diese Laufleistung erreicht, beträgt:

$P(6120 \leq H)\approx 0,00077 =0,077\,\%$

Die Aussage für die Vorderrad- und Hinterradreifen des Herstellers ist somit wahr.

Aus dem Graphen kann abgelesen werden:

$\begin{array}[t]{rll} f(5,5)&=& 0,5 & \\[5pt] P(Z\leq 1000\cdot 5,5)&=& 0,5 & \\[5pt] P(Z\leq 5500)&=& 0,5 & \end{array}$

Da die Normalverteilung symmetrisch um den Erwartungswert $\mu_Z$ ist und $f(5,5)= 0,5$ gilt, muss $\mu_Z=5,5$ sein.

Weiterhin kann aus der Abbildung abgelesen werden:

$\begin{array}[t]{rll} f(5)&\approx& 0,1& \\[5pt] P(Z\leq 5000)&\approx& 0,1 \end{array}$

Systematisches Ausprobieren mit dem Taschenrechner liefert mit $\mu_Z=5,5:$

Für $\sigma_Z=390: \quad P(Z\leq 5000)\approx 0,09991$

Für $\sigma_Z=391: \quad P(Z\leq 5000)\approx 0,10049$

Der Erwartungswert und die Standardabweichung folgen also mit $\mu_Z=5500\,\text{km}$ und $\sigma_Z=390\,\text{km}.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?