Pflichtaufgabe 2 - Analytische Geometrie

Ein Kirchturm mit einem quaderförmigen Baukörper und quadratischer Grundfläche (Seitenlänge $6\,\text{m}$ ) soll restauriert werden. Die auf den Baukörper aufgesetzten Giebelwände haben die Form gleichschenkliger Dreiecke und sind jeweils $2\,\text{m}$ hoch. Jede der viereckigen Dachflächen ist eben.

Die Beschreibung des Kirchturmes erfolgt in einem dreidimensionalen kartesischen Koordinatensystem (eine Einheit entspricht einem Meter, die Horizontalebene entspricht der $xy$ -Ebene).
Der Koordinatenursprung markiert die Lage des Mittelpunktes der Grundfläche des Baukörpers und die Seiten der Grundfläche verlaufen parallel zur $x$ - bzw. $y$ -Achse.

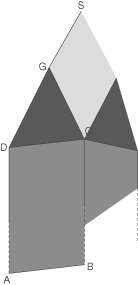
Geometrische Darstellung eines Polyeders mit mehreren Ebenen und Punkten.

Die Eckpunkte einer Seite des Kirchturmes seien mit $A(3\mid -3\mid 0)$ , $B$ , $C(3\mid 3\mid 15)$ und $D$ sowie $G(3\mid 0 \mid 17)$ als Giebelspitze beschrieben. Die Spitze des Kirchturmdaches wird durch den Punkt $S(0\mid 0\mid 20)$ beschrieben.

a) Gib die Koordinaten der Punkte $B$ und $D$ sowie die Höhe des quaderförmigen Baukörpers an.

b) Eine Ebene $\varepsilon$ enthält die Punkte $C$ , $G$ und $S$ .
Ermittle eine Koordinatengleichung der Ebene $\varepsilon$ .

Die Ebene $\varepsilon$ beschreibt die Lage einer der vier Dachflächen des Kirchturms.
Berechne den Inhalt einer der Dachflächen.

Von der Spitze ausgehend werden Spannseile bis zum Erdboden geführt, die auf den Kanten des Daches liegen. Die Spannseile können als Seitenkanten einer vierseitigen, auf der $xy$ -Ebene stehenden Spannseil-Pyramide aufgefasst werden.

c) Die Gerade $GS$ beschreibt die Lage eines der Spannseile.

Gib eine Gleichung der Geraden $GS$ an und berechne das Gradmaß des Winkels, den die Gerade $GS$ mit der $xy$ -Ebene einschließt.

Berechne sowohl die Koordinaten des Ankerpunktes eines solchen Spannseils als auch die Länge eines Spannseils.

d) Die nicht maßstäblichen Abbildungen zeigen Grundrisse von Pyramiden; die grauen Quadrate veranschaulichen den Grundriss des Baukörpers.
Genau eine der drei Abbildungen zeigt die Lage der Spannseil-Pyramide bezüglich des Baukörpers. Gib an und begründe, welche der Abbildungen dies ist.

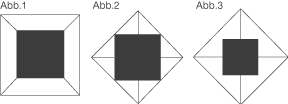
Drei geometrische Abbildungen, die unterschiedliche Formen und Anordnungen zeigen.

a) $\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{B}$ bestimmen

Du sollst die Koordinaten des Punktes $B$ bestimmen. Dieser Punkt ist ein Eckpunkt der quadratischen Grundfläche des Kirchturms. Er hat somit die gleiche $x$ - und die gleiche $z$ -Koordinate wie der Punkt $A$ . Die Seitenlänge der Grundfläche beträgt 6m. Du erhältst die Koordinaten des Punktes $B$ also, indem du Punkt $A$ um 6 in positive $y$ - Richtung verschiebst.

$B(3\mid 3 \mid 0)$

$\blacktriangleright$ Koordinaten des Punktes $\boldsymbol{D}$ bestimmen

Du erhältst die Koordinaten des Punktes $D$ , indem du Punkt $C$ um 6 in negative $y$ - Richtung verschiebst.

$D(3\mid -3 \mid 15)$

$\blacktriangleright$ Höhe des quaderförmigen Bauteils

Die Höhe des quaderförmigen Bauteils erhältst du indem du den Abstand der $z$ -Koordinaten der Punkte $A$ und $D$ bzw. $B$ und $C$ bestimmst.

Die Höhe des quaderförmigen Bauteils beträgt somit 15 m.

b) $\blacktriangleright$ Ebenengleichung in Koordinatenform bestimmen

Du sollst die Gleichung der Ebene durch die Punkte $C$ , $G$ und $S$ in Koordinatenform bestimmen. Die allgemeine Gleichung einer Ebene in Koordinatenform lautet $\color{#87c800}{\boldsymbol{ax+by+cz=d}}$ . Setze die Punkte ein und berechne die Parameter, du erhältst dann folgendes Gleichungssystem:

$\begin{array}{lcccccccl} \text{I}\quad&3a&+&3b&+&15c&=&d&\quad\\ \text{II}\quad&3a&&&+&17c&=&d&\quad\\ \text{III}\quad&&&&&20c&=&d&\quad \scriptsize\mid\;\text{Setze III in II ein}\\ \hline \text{I}\quad&3a&+&3b&+&15c&=&d&\quad\\ \text{IIa}\quad&3a&&&+&17c&=&20c&\quad \scriptsize\mid\; -17c\\ \text{III}\quad&&&&&20c&=&d&\quad \\ \hline \text{I}\quad&3a&+&3b&+&15c&=&d&\quad\\ \text{IIa}\quad&3a&&&&&=&3c&\quad \Rightarrow a=c\\ \text{III}\quad&&&&&20c&=&d&\quad \scriptsize\mid\;\text{Setze III und IIa in I ein}\\ \hline \text{Ia}\quad&3c&+&3b&+&15c&=&20c&\quad\\ \text{IIa}\quad&a&&&&&=&c&\\ \text{III}\quad&&&&&20c&=&d&\quad \scriptsize\mid\;\text{Löse I nach }b\text{ auf}\\ \hline \end{array}$

Du erhältst somit:

$\begin{array}[t]{rll} b&=&\frac{2}{3}c \\[5pt] a&=&c\\[5pt] d&=&20c \end{array}$

Wähle $c=3$ und du erhältst folgende Ebenengleichung:

$\begin{array}[t]{rll} b&=&\frac{2}{3}3 = 2 \\[5pt] a&=&3\\[5pt] d&=&60 \end{array}$

$\varepsilon:\quad 3x + 2y +3c = 60$ .

$\blacktriangleright$ Flächeninhalt berechnen

Du sollst den Inhalt einer Dachfläche berechnen. Bei dieser Fläche handelt es sich um eine Drachenfläche, deren Inhalt durch folgende Formel berechnet werden kann:

$A = \dfrac{1}{2}\cdot e \cdot f$

wobei $e$ und $f$ die Verbindungsstrecken der sich gegenüberliegenden Eckpunkten sind.

Das Dreieck aus den Punkten $C$ , $D$ und $G$ ist gleichschenklig, das bedeutet, dass der Punkt $G$ oberhalb des Mittelpunktes der Strecke von $C$ nach $D$ liegt. Außerdem ist die Länge dieser Streck 6m. Der unbekannte Punkt der Dachfläche befindet sich somit auch oberhalb des Mittelpunkts einer Strecke, deren Länge 6m beträgt. Skizziere dir diese Situation, um anschließend die Länge der Strecke zwischen $G$ und dem unbekannten Punkt zu berechnen.

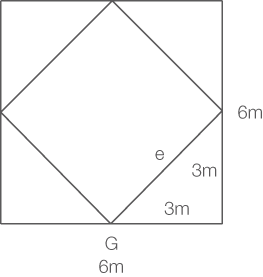Diagramm eines Raumes mit einem Quadrat und einem inneren Rhombus, Maße in Metern angegeben.

Die Länge von $e$ kannst du mit Hilfe des Satz von Pythagoras berechnen.

$\begin{array}[t]{rll} e^2&=&3^2 + 3^2 \\[5pt] e^2&=&2\cdot 9\quad \scriptsize \mid\;\sqrt{ }\\[5pt] e&=&3\sqrt{2} \end{array}$

Die Diagonale $f$ entspricht der Länge des Vektors $\overrightarrow{CS}$ .

$f=\mid \overrightarrow{CS} \mid = \left|\begin{pmatrix}0-3\\0-3\\20-5\end{pmatrix}\right| = \sqrt{(-3)^2 + (-3)^2 + 5^2} = \sqrt{43}$

Für den Inhalt der Dachfläche ergibt sich somit:

$A= \dfrac{1}{2} \cdot 3 \sqrt{2} \cdot \sqrt{43} \approx 13,91$

Der Inhalt der Dachfläche beträgt ungefähr 13,91 m².

c) $\blacktriangleright$ Gleichung der Geraden bestimmen

Du sollst die Gleichung der Gerade $GS$ eines Spannseils bestimmen. Ein Spannseil wird von der Spitze des Turms zum Boden gespannt. Die Gerade verläuft somit durch den Punkt $S$ , das liefert dir den Stützvektor $\overrightarrow{OS}$ . Das Spannseil wird auf der Kante des Dachs entlang geführt, eine dieser Kanten ist beispielsweise von $G$ nach $S$ , somit kannst du $\overrightarrow{SG}$ als Richtungsvektor für die Gerade GS verwenden.

$\begin{array}[t]{lrll} GS:\quad&\vec{x}&=&\overrightarrow{OS} + r \cdot \overrightarrow{SG}\\[5pt] &\vec{x}&=&\begin{pmatrix}0\\0\\20\end{pmatrix} + r \begin{pmatrix}3-0\\0-0\\17-20\end{pmatrix}\\[5pt] &\vec{x}&=&\begin{pmatrix}0\\0\\20\end{pmatrix} + r \begin{pmatrix}3\\0\\-3\end{pmatrix} \end{array}$

$\blacktriangleright$ Winkel berechnen

Du sollst nun das Gradmaß des Winkels , den die Gerade $GS$ mit der $xy$ -Ebene einschließt berechnen.

Für die Berechnung eines Winkels zwischen einer Gerade und einer Ebene kannst du folgende Formel verwenden

$\alpha = \arcsin\left(\dfrac{\mid \vec{u}\cdot \vec{n}\mid}{\mid\vec{u} \mid \cdot \mid \vec{n}\mid}\right)$

wobei $\vec{u}$ der Richtungsvektor der Geraden und $\vec{n}$ der Normalenvektor der Ebene darstellt.

Bestimme also zunächst den Normalenvektor und berechne dann den Winkel.

1. Schritt: Normalvektor bestimmen

Der Normalenvektor einer Ebene ist orthogonal zur Ebene. Ein Normalenvektor der $xy$ - Ebene ist somit

$\vec{n} = \begin{pmatrix}0\\0\\1\end{pmatrix}$ .

2. Schritt: Winkel berechnen

Der Richtungsvektor der Geraden lautet

$\vec{u} = \begin{pmatrix}3\\0\\-3\end{pmatrix}$ .

Setze nun $\vec{u}$ und $\vec{n}$ in die Formel ein und Berechne $\alpha$ .

$\begin{array}[t]{rll} \alpha&=& \arcsin\left(\dfrac{ \left| \begin{pmatrix}3\\0\\-3\end{pmatrix}\cdot \begin{pmatrix}0\\0\\1\end{pmatrix}\right|}{ \left|\begin{pmatrix}3\\0\\-3\end{pmatrix} \right| \cdot \left|\begin{pmatrix}0\\0\\1\end{pmatrix}\right|}\right) \\[5pt] &=&\arcsin\left(\dfrac{\mid 3\cdot 0 + 0 \cdot 0 + (-3) \cdot 1\mid}{\sqrt{3^2 + (-3)^2} \cdot 1}\right)\\[5pt] &=&\arcsin\left(\dfrac{3}{\sqrt{18}}\right)\\[5pt] &=& \arcsin\left(\dfrac{3}{3\sqrt{2}}\right)\\[5pt] &=&45^{\circ} \end{array}$

Das Gradmaß des gesuchten Winkels beträgt $45^{\circ}$ .

$\blacktriangleright$ Ankerpunkt berechnen

Der Ankerpunkt entspricht dem Schnittpunkt der Geraden $GS$ mit der $xy$ -Ebene. Es muss also $\color{#87c800}{\boldsymbol{z=0}}$ gelten, der Punkt hat folgende Form

$A(x_A \mid y_A \mid 0)$ .

Setze den Punkt mit der Gleichung der Geraden gleich und berechne aus der dritten Zeile den Parameter $r$ .

$\begin{pmatrix}x_A\\y_A\\0\end{pmatrix} = \begin{pmatrix}0\\0\\20\end{pmatrix} + r \begin{pmatrix}3\\0\\-3\end{pmatrix}$

$\begin{array}[t]{rll} 0&=&20-3r \quad \scriptsize \mid\; +3r\\[5pt] 3r&=&20\quad \scriptsize \mid\; :3\\[5pt] r&=&\frac{20}{3} \end{array}$

Setze nun $r=\frac{20}{3}$ in die Geradengleichung ein um die Koordinaten des Ankerpunkts zu berechnen.

$\begin{pmatrix}0\\0\\20\end{pmatrix} + \frac{20}{3} \begin{pmatrix}3\\0\\-3\end{pmatrix} = \begin{pmatrix}20 \\ 0 \\ 0\end{pmatrix}$

Die Koordinaten des Ankerpunkts lauten $A(20 \mid 0 \mid 0)$ .

$\blacktriangleright$ Länge eines Ankerseils berechnen

Die Länge $l$ des Ankerseils entspricht der Entfernung zwischen dem Ankerpunkt $A$ und der Spitze $S$ .

$l = \mid \overrightarrow{AS} \mid = \left| \begin{pmatrix}0 \\ 0 \\ 20\end{pmatrix}-\begin{pmatrix}20 \\ 0 \\ 0\end{pmatrix}\right| = \left| \begin{pmatrix}-20 \\ 0 \\ 20\end{pmatrix}\right| = \sqrt{(-20)^2 + 0^2 + 20^2} = \sqrt{800} \approx 28,28$

Die Länge eines Spannseils beträgt ungefähr 28,28 m.

d) $\blacktriangleright$ Grundriss zuordnen

Du sollst den Grundriss der Spannseilpyramide identifizieren.

Zuerst fällt auf, dass die Spannseile entlang der Kanten des Turms verlaufen und somit in der Mitte des quaderförmigen Bauteils. Somit kann Abbildung 1 ausgeschlossen werden.

Betrachte nun die Grundfläche des quaderförmigen Bauteils. Bei Abbildung 2 liegen die Eckpunkte dieses Bauteils auf den Kanten der Grundfläche der Pyramide, genauer gesagt in der Mitte der Kante. Einer dieser Punkte hat beispielsweise die Koordinaten $(10 \mid -10 \mid 0)$ , Punkt $A$ lautet jedoch $(3 \mid -3 \mid 0)$ . Die Grundfläche des quaderförmigen Bauteils liegt also innerhalb des Grundrisses der Spannseilpyramide.

Die passende Abbildung ist Abbildung 3.