Pflichtaufgaben
1.
Gegeben ist die in 
definierte Funktion 
mit 
Der Graph von wird mit 
bezeichnet.
a)
Gib das Verhalten von für 
an.
(1 BE)
b)
Gib die Koordinaten des Schnittpunkts von mit der 
-Achse an.
(1 BE)
c)
Untersuche, ob die Steigung von in jedem Punkt von kleiner als 3 ist.
(3 BE)
2.
Gegeben ist die in definierte Funktion mit 
und 
Die Nullstellen von sind 
und 
.
a)
Zeige, dass das Flächenstück, das der Graph von mit der 
-Achse einschließt, den Inhalt 
hat.
(2 BE)
b)
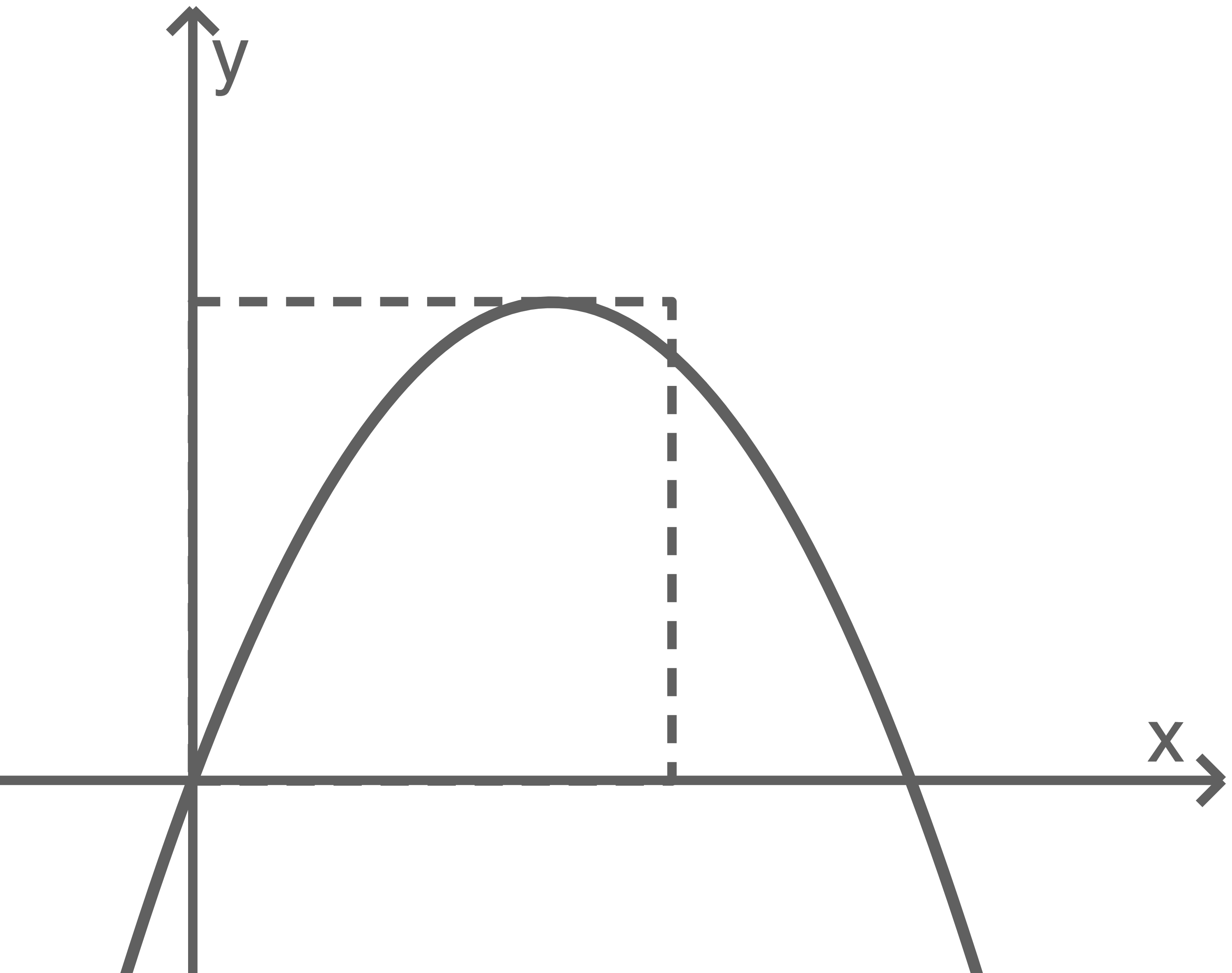
Der Hochpunkt des Graphen von liegt auf einer Seite eines Quadrats; zwei Seiten dieses Quadrats liegen auf den Koordinatenachsen (vgl. Abbildung).
Der Flächeninhalt des Quadrats stimmt mit dem Inhalt des Flächenstücks, das der Graph von mit der -Achse einschließt, überein.
Bestimme den Wert von 
(3 BE)
3.
Gegeben ist die Gerade 
mit 
a)
Zeige, dass 
in der Ebene mit der Gleichung 
liegt.
(2 BE)
b)
Gegeben ist außerdem die Schar der Geraden 
mit 
und 
Weise nach, dass und 
für jeden Wert von 
windschief sind.
(3 BE)
4.
In einem Behälter befinden sich fünf Kugeln, auf denen jeweils eine Zahl steht. Auf drei der Kugeln steht die Zahl 2, auf zwei der Kugeln die negative Zahl
Zweimal nacheinander wird eine Kugel zufällig entnommen und wieder zurückgelegt.
a)
Gib im Sachzusammenhang ein Ereignis an, dessen Wahrscheinlichkeit mit dem Term 
berechnet werden kann.
(1 BE)
b)
Die Zufallsgröße 
gibt das Produkt der Zahlen an, die auf den beiden entnommenen Kugeln stehen. Der Erwartungswert von ist 4.
Bestimme den Wert von
(4 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
1.
a)
Es gilt:
Somit folgt für das Verhalten von für 
b)
c)
Ableitung bilden:
Da 
gilt, folgt für 
Die Steigung von ist somit in jedem Punkt von kleiner als 3.
2.
a)
Der Inhalt des Flächenstücks lässt sich wie folgt berechnen:
b)
1. Schritt: Koordinaten des Hochpunkts ermitteln
Aus den Nullstellen bei 
und 
ergibt sich aufgrund der Symmetrie ein Hochpunkt mit den Koordinaten 
Die -Koordinate ergibt sich zu:
![\(\begin{array}[t]{rll}
f(a)&=& -a^2+2a\cdot a& \\[5pt]
&=& a^2
\end{array}\)](https://mathjax.schullv.de/1fdff1ec86f7930b53cc12bf125b98ffe63ac768387207047bb19083d322d418?color=5a5a5a)
2. Schritt: Wert von bestimmen
Für den Flächeninhalt des Quadrates gilt:
![\(A_Q=A=\dfrac{4}{3}a^3 \; [\text{FE}]\)](https://mathjax.schullv.de/a31d9e95c211883f892551b2f73c15b20628e04f8cd9a72cd30dccdef36b1307?color=5a5a5a)
Mit den Koordinaten des Hochpunkts 
ergeben sich die Höhe und somit auch die Breite des Quadrats mit 
Es folgt 
und somit:
![\(\begin{array}[t]{rll}
A_Q&=& \dfrac{4}{3}a^3&\\[5pt]
a^2\cdot a^2&=& \dfrac{4}{3}a^3 & \\[5pt]
a^4&=& \dfrac{4}{3}a^3&\quad \scriptsize \mid\; :a^3\\[5pt]
a&=&\dfrac{4}{3}
\end{array}\)](https://mathjax.schullv.de/85c8031930e5bd4dca46d4fcbb59cfb743f8438db06e6ac4eada96325c3f119d?color=5a5a5a)
3.
a)
Aus der Geradengleichung lassen sich 
und 
herauslesen.
Einsetzen in die Ebenengleichung ergibt:
![\(\begin{array}[t]{rll}
E: \lambda+1+(1-\lambda)&=& 2& \\[5pt]
2&=& 2
\end{array}\)](https://mathjax.schullv.de/b2a6549a57bd092be0f1a5c6cb318d1e2234913bfc690c28900709ee2605901b?color=5a5a5a)
Somit liegt die Gerade in der Ebene 
b)
Zwei Geraden sind genau dann windschief, wenn sie nicht parallel bzw. identisch parallel zueinander sind und keinen gemeinsamen Schnittpunkt haben.
Parallelität überprüfen:
Es muss gelten:
Da aus der ersten Zeile 
, aus der zweiten Zeile 
und aus der dritten Zeile 
folgt, hat diese Gleichung keine Lösung.
Die Gerade und die Geraden der Schar sind folglich unabhängig von weder parallel noch identisch parallel zueinander.
Schnittpunkt prüfen:
Aus der dritten Zeile folgt 
und eingesetzt in die erste Zeile 
Einsetzen in die zweite Zeile ergibt jedoch 
was zu einem Widerspruch führt.
Die Gerade und die Geraden der Schar haben somit keinen Schnittpunkt miteinander und sind folglich für jeden Wert von windschief.
4.
a)
„Es werden zwei Kugeln aus dem Behälter gezogen, die mit unterschiedlichen Zahlen beschriftet sind."
b)