Wahlpflichtaufgaben
5.1
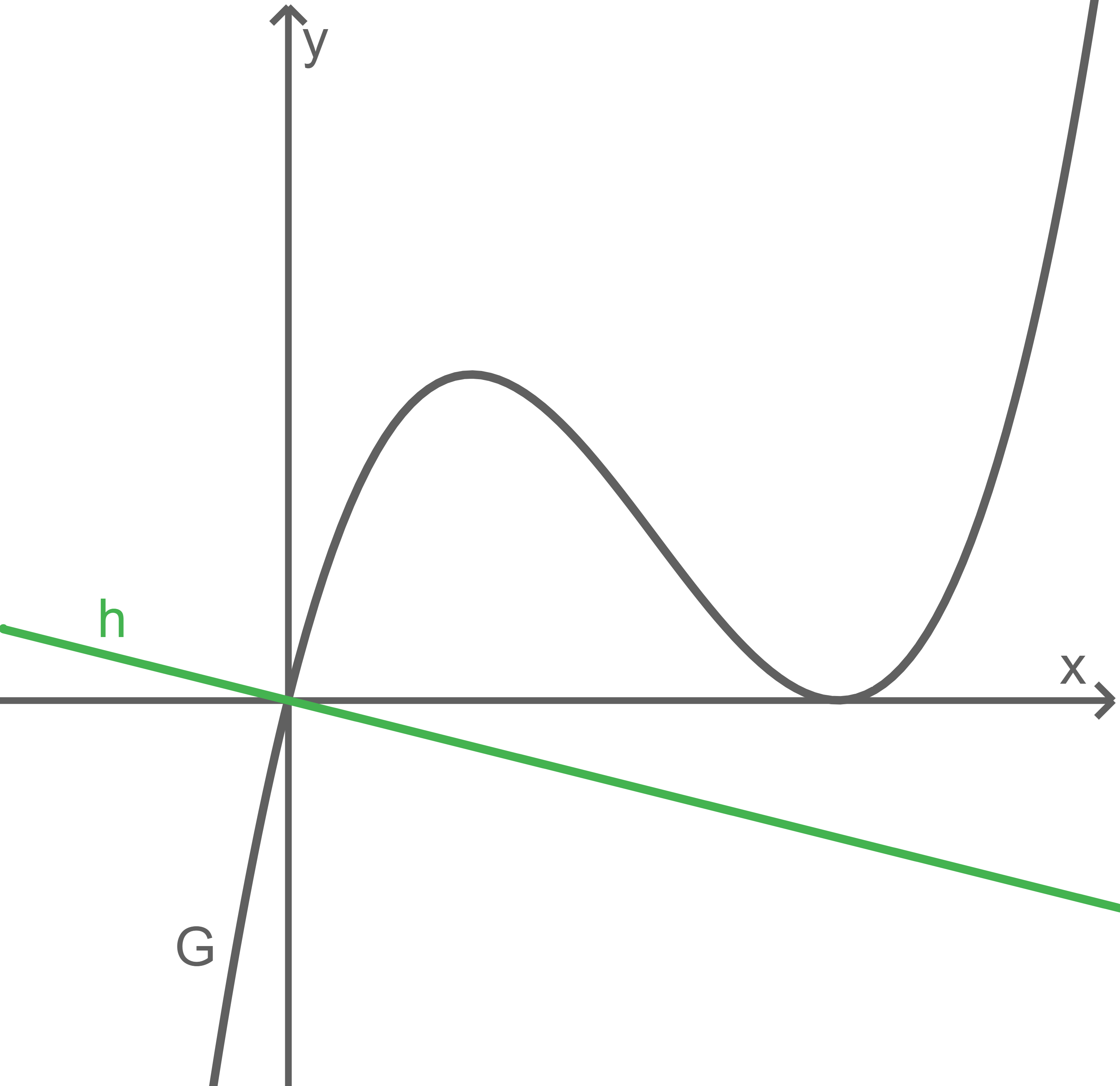
Für eine reelle Zahl  zeigt die Abbildung den Graphen
zeigt die Abbildung den Graphen  der in
der in  definierten Funktion
definierten Funktion  mit
mit  sowie die Gerade
sowie die Gerade 
 und
und  schneiden sich im Koordinatenursprung und
schneiden sich im Koordinatenursprung und  verläuft senkrecht zur Tangente an
verläuft senkrecht zur Tangente an  im Koordinatenursprung. Zudem berühren sich
im Koordinatenursprung. Zudem berühren sich  und die
und die  -Achse im Punkt
-Achse im Punkt  Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
Betrachtet wird dasjenige Rechteck, das die folgenden Eigenschaften besitzt:
 ist.
ist.

- Die beiden gemeinsamen Punkte von
und der
-Achse sind zwei benachbarte Eckpunkte des Rechtecks.
- Eine Diagonale liegt auf der Gerade
(5 BE)
5.2
Die in  definierte Funktion
definierte Funktion  hat die erste Ableitungsfunktion
hat die erste Ableitungsfunktion  mit
mit  und es gilt
und es gilt  Leitet man die erste Ableitungsfunktion
Leitet man die erste Ableitungsfunktion  ab, so erhält man die zweite Ableitungsfunktion
ab, so erhält man die zweite Ableitungsfunktion  von
von  Entsprechend entsteht die hundertste Ableitungsfunktion
Entsprechend entsteht die hundertste Ableitungsfunktion  von
von  Der Graph der hundertsten Ableitungsfunktion
Der Graph der hundertsten Ableitungsfunktion  lässt sich aus dem Graphen von
lässt sich aus dem Graphen von  durch eine Verschiebung in
durch eine Verschiebung in  -Richtung erzeugen.
Ermittle, um wie viele Einheiten der Graph von
-Richtung erzeugen.
Ermittle, um wie viele Einheiten der Graph von  dazu in
dazu in  -Richtung zu verschieben ist.
-Richtung zu verschieben ist.
(5 BE)
5.3
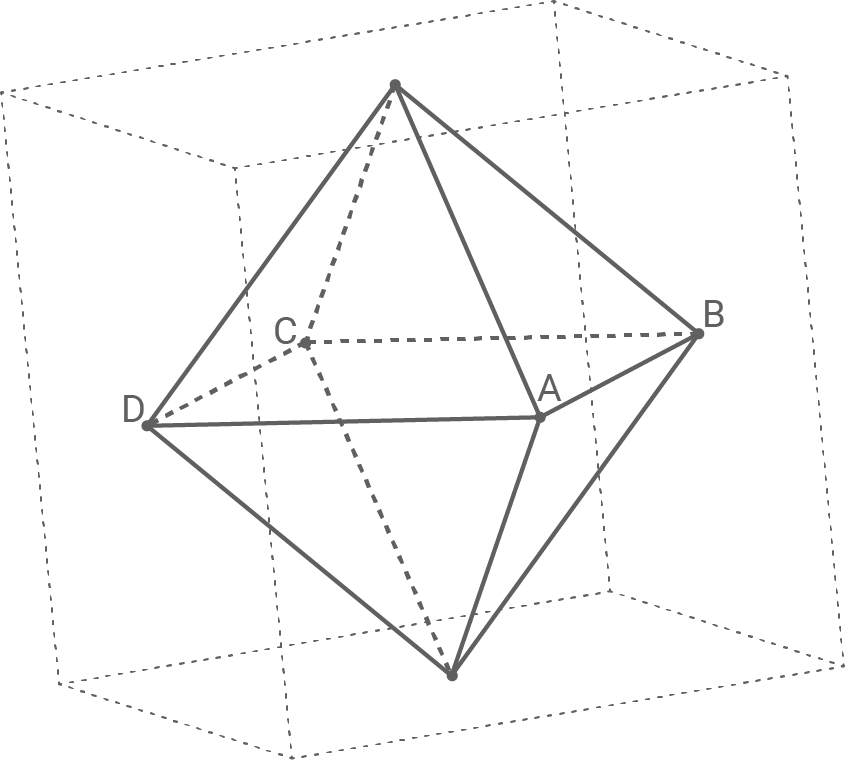
Mittelpunkte der Seitenflächen eines Würfels sind die Eckpunkte eines Oktaeders (vgl. Abbildung).
Die Eckpunkte 

 und
und  des Oktaeders liegen in der Ebene
des Oktaeders liegen in der Ebene  mit der Gleichung
mit der Gleichung 

a)
Weise nach, dass die Kantenlänge des Würfels 12 beträgt.
(2 BE)
b)
Bestimme die Koordinaten eines der beiden Eckpunkte des Oktaeders, die nicht in  liegen.
liegen.
(3 BE)
5.4
Die Abbildung zeigt die Punkte  und
und  Die Ebene, in der die drei Punkte liegen, wird durch die Zeichenebene dargestellt.
Die Ebene, in der die drei Punkte liegen, wird durch die Zeichenebene dargestellt.
 Betrachtet werden Geraden
Betrachtet werden Geraden  und
und  für die gilt:
für die gilt:
 die Gerade
die Gerade  und eine Gerade
und eine Gerade  in die Abbildung ein.
Gib einen Term an, mit dem aus den gegebenen Punkten
in die Abbildung ein.
Gib einen Term an, mit dem aus den gegebenen Punkten  und
und  der Ortsvektor eines weiteren Punktes von
der Ortsvektor eines weiteren Punktes von  bestimmt werden kann.
bestimmt werden kann.

verläuft durch
durch
und
durch
und
schneiden sich in
- Wird
an
gespiegelt, so entsteht
.
(5 BE)
5.5
Vor der Wahl des Oberbürgermeisters einer Stadt möchte ein Kandidat durch eine statistische Erhebung seinen aktuellen Stimmenanteil unter allen Wahlberechtigten schätzen. Dazu wird unter allen wahlberechtigten Bewohnern eines Seniorenheimes dieser Stadt eine Befragung durchgeführt, ob diese den Kandidaten wählen werden.
a)
Gib für diese statistische Erhebung die Grundgesamtheit und die Stichprobe an.
(2 BE)
b)
Beurteile folgende Aussage:
Aus dem Ergebnis der Befragung lässt sich auf den aktuellen Stimmenanteil des Kandidaten bei der Oberbürgermeisterwahl schließen.
(3 BE)
5.6
Die drei nicht sichtbaren Seiten des abgebildeten Würfels sollen jeweils mit einer der Zahlen 3, 4, 5 oder 6 beschriftet werden. Dabei können Zahlen auch mehrfach verwendet werden.
 Nach der Beschriftung soll der Würfel folgende Eigenschaften haben:
Nach der Beschriftung soll der Würfel folgende Eigenschaften haben:
Untersuche, ob es möglich ist, die nicht sichtbaren Seiten des Würfels so zu beschriften, dass er alle drei Eigenschaften besitzt.

- Beim einmaligen Werfen ist der Erwartungswert für die erzielte Zahl gleich 4.
- Auf den sechs Seiten des Würfels kommen genau drei verschiedene Zahlen vor.
- Die Wahrscheinlichkeit dafür, dass beim zweimaligen Werfen des Würfels zweimal die gleiche Zahl erzielt wird, beträgt
(5 BE)
Weiter lernen mit SchulLV-PLUS!
monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?
5.1
Rechteck skizzieren
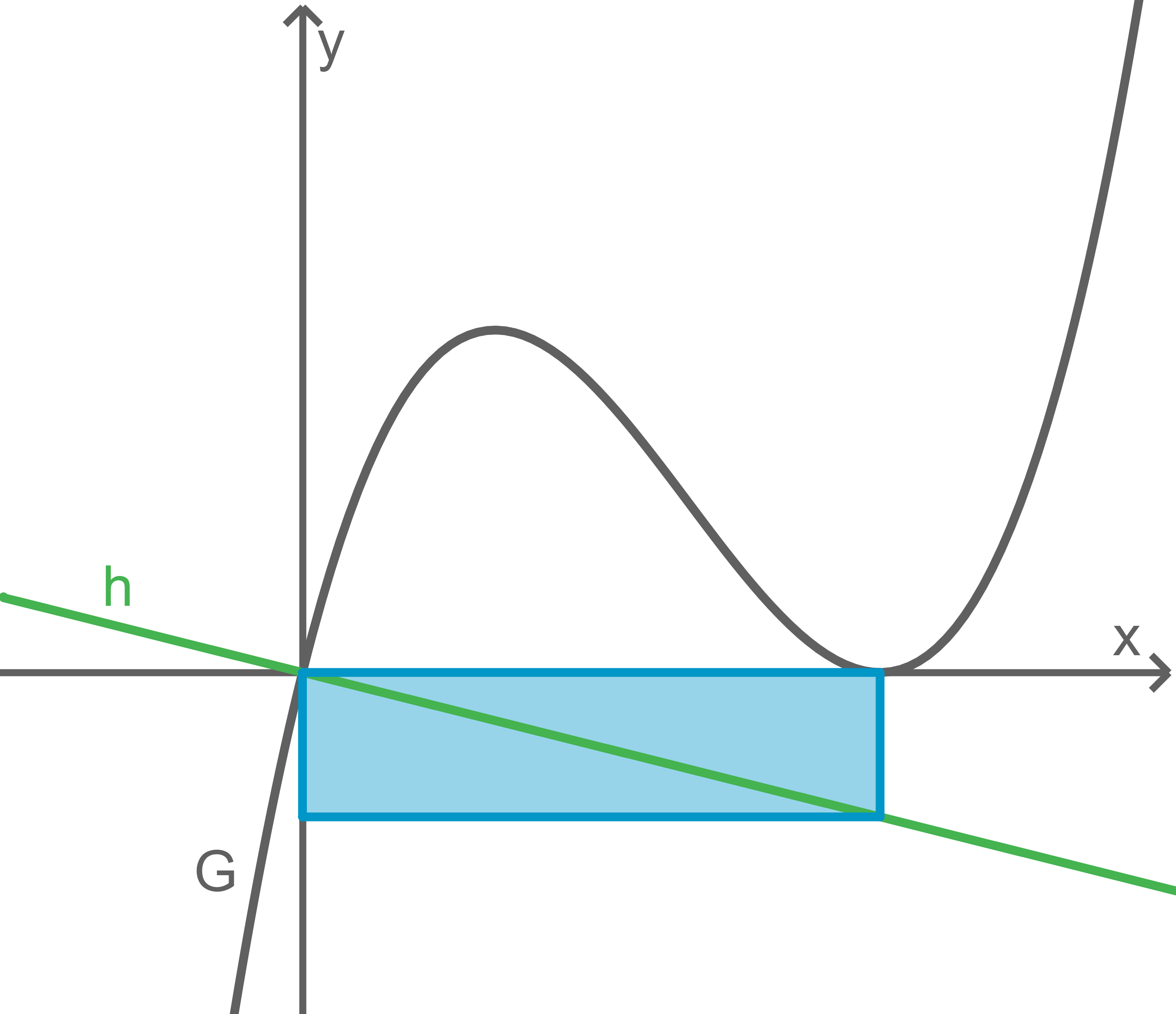 Unabhängigkeit zeigen
Die Länge der Seite des Rechtecks, die auf der
Unabhängigkeit zeigen
Die Länge der Seite des Rechtecks, die auf der  -Achse liegt, ergibt sich durch die Differenz der
-Achse liegt, ergibt sich durch die Differenz der  -Werte der beiden Punkte, in denen
-Werte der beiden Punkte, in denen  die
die  -Achse berührt, und entspricht somit
-Achse berührt, und entspricht somit  Für die Ableitung der Funktion
Für die Ableitung der Funktion  gilt:
gilt:
 Da
Da  senkrecht zur Tangente an
senkrecht zur Tangente an  im Koordinatenursprung verläuft, ergibt sich mit Hilfe von
im Koordinatenursprung verläuft, ergibt sich mit Hilfe von  die Steigung
die Steigung  von
von 
 Eine Gleichung der Tangente folgt also mit
Eine Gleichung der Tangente folgt also mit  Die Höhe des Rechtecks entspricht dem Betrag des Funktionswerts von
Die Höhe des Rechtecks entspricht dem Betrag des Funktionswerts von  an der Stelle
an der Stelle  Es gilt also:
Es gilt also:
 Damit folgt für den Flächeninhalt
Damit folgt für den Flächeninhalt  des Rechtecks
des Rechtecks  womit dieser unabhängig von
womit dieser unabhängig von  ist.
ist.

5.2
1. Schritt: Funktion  bestimmen
Die Funktion von
bestimmen
Die Funktion von  ergibt sich zu
ergibt sich zu  Wegen
Wegen  folgt:
folgt:
![\(\begin{array}[t]{rll}
f(0)&=& 1 &\\[5pt]
\mathrm e^{2\cdot 0}+c&=& 1 &\\[5pt]
1+c&=& 1 &\quad \scriptsize \mid -1\\[5pt]
c&=& 0
\end{array}\)](https://mathjax.schullv.de/24bb4a31b36c7d6f431ae551b6b6f956cb4d35a411e2a3d26db0c32dfd04cf9f?color=5a5a5a) 2. Schritt: Muster untersuchen
Es gilt also:
2. Schritt: Muster untersuchen
Es gilt also:
![\(\begin{array}[t]{rll}
f(x)&=& \mathrm e^{2x} & \\[5pt]
f](https://mathjax.schullv.de/3f5b7b6e40cc54cfa7a11cef4a13dd77c348b0e77d305a580554ce36db998306?color=5a5a5a) Aus den ersten drei Ableitungen von
Aus den ersten drei Ableitungen von  ergibt sich folgendes Muster:
ergibt sich folgendes Muster:
 Für die hundertste Ableitungsfunktion folgt also:
Für die hundertste Ableitungsfunktion folgt also:
 3. Schritt: Verschiebung berechnen
Für den Graph der Funktion
3. Schritt: Verschiebung berechnen
Für den Graph der Funktion  gilt
gilt  Um die Verschiebung in
Um die Verschiebung in  -Richtung zu untersuchen, muss berechnet werden, an welcher Stelle die hundertste Ableitungsfunktion den Wert 1 annimmt:
-Richtung zu untersuchen, muss berechnet werden, an welcher Stelle die hundertste Ableitungsfunktion den Wert 1 annimmt:
![\(\begin{array}[t]{rll}
f^{(100)}(x)&=& 1& \\[5pt]
2^{100}\cdot \mathrm e^{2x}&=& 1&\quad \scriptsize \,\bigg \vert \,\; :2^{100}\\[5pt]
\mathrm e^{2x}&=& \dfrac{1}{2^{100}}&\quad \scriptsize \,\bigg \vert \,\; \ln(\;)\\[5pt]
2x&=& \ln\left(\dfrac{1}{2^{100}}\right)&\quad \scriptsize \,\bigg \vert \, \; \cdot \dfrac{1}{2}\\[5pt]
x&=& \dfrac{1}{2}\cdot \ln\left(\dfrac{1}{2^{100}}\right)
\end{array}\)](https://mathjax.schullv.de/8b1355214b04d50b870b415b0478fd827ac4dd4b5d38023054c2f602433cbde3?color=5a5a5a) Der Graph von
Der Graph von  muss also um
muss also um  in negative
in negative  -Richtung verschoben werden.
-Richtung verschoben werden.
5.3
a)
Die Kantenlänge des Würfels entspricht der Strecke  Für diese gilt:
Für diese gilt:
![\(\begin{array}[t]{rll}
\left\vert\overrightarrow{AC}\right\vert&=&\left\vert\pmatrix{-3\\-6\\9}-\pmatrix{1\\2\\1}\right\vert \\[5pt]
&=&\left\vert\pmatrix{-4\\-8\\8}\right\vert \\[5pt]
&=&\sqrt{(-4)^2+(-8)^2+8^2} \\[5pt]
&=&\sqrt{144} \\[5pt]
&=& 12 \;[\,\text{LE}]
\end{array}\)](https://mathjax.schullv.de/7b7767f52a8b369ab6a853045708329a554e0889fc03462420fe1df52f0b1db5?color=5a5a5a)
b)
Punkte, die nicht in  liegen, sind die obere bzw. die untere Spitze des Oktaeders und liegen senkrecht über dem Mittelpunkt von
liegen, sind die obere bzw. die untere Spitze des Oktaeders und liegen senkrecht über dem Mittelpunkt von  Für den Mittelpunkt
Für den Mittelpunkt  der Strecke
der Strecke  gilt:
gilt:
![\(\begin{array}[t]{rll}
\overrightarrow{OM}&=&\overrightarrow{OA}+\dfrac{1}{2}\cdot\overrightarrow{AC} \\[5pt]
&=&\pmatrix{1\\2\\1}+\dfrac{1}{2}\cdot\pmatrix{-4\\-8\\8} \\[5pt]
&=&\pmatrix{-1\\-2\\5}
\end{array}\)](https://mathjax.schullv.de/f13901135af0ed1192f659481eb360c4523f0a812f6d7c78db8b4d46d714bd89?color=5a5a5a) Aus der Ebenengleichung von
Aus der Ebenengleichung von  kann der Normalenvektor
kann der Normalenvektor  abgelesen werden. Dieser steht senkrecht zur Ebene
abgelesen werden. Dieser steht senkrecht zur Ebene  und besitzt die Länge:
und besitzt die Länge:
![\(\begin{array}[t]{rll}
\vert\overrightarrow{n}\vert&=& \sqrt{2^2+1^2+2^2} & \\[5pt]
&=& \sqrt{9} & \\[5pt]
&=& 3
\end{array}\)](https://mathjax.schullv.de/63cd183ca0dc688eff99f9340f4ebdd3e7e68edef9148a369b19146226cc0544?color=5a5a5a) Da die Kantenlänge des Würfels
Da die Kantenlänge des Würfels  beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu
beträgt, ist der Abstand des gesuchten Eckpunktes des Oktaeders zu  durch 6 Längeneinheiten, also der doppelten Länge des Normalenvektors, gegeben.
Ein möglicher Ortsvektor der oberen Spitze
durch 6 Längeneinheiten, also der doppelten Länge des Normalenvektors, gegeben.
Ein möglicher Ortsvektor der oberen Spitze  folgt also mit:
folgt also mit:
![\(\begin{array}[t]{rll}
\overrightarrow{OS}&=& \overrightarrow{OM}+2\cdot\overrightarrow{n}& \\[5pt]
&=& \pmatrix{-1\\-2\\5}+2\cdot\pmatrix{2\\1\\2}& \\[5pt]
&=& \pmatrix{3\\0\\9}
\end{array}\)](https://mathjax.schullv.de/9a0c626fcfb7174bfa637583d2d3e5d5db3ca8f86df8253c35f2e8d468c8216b?color=5a5a5a) Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch
Mögliche Koordinaten für den gesuchten Punkt sind somit gegeben durch 
5.4
Geraden einzeichnen
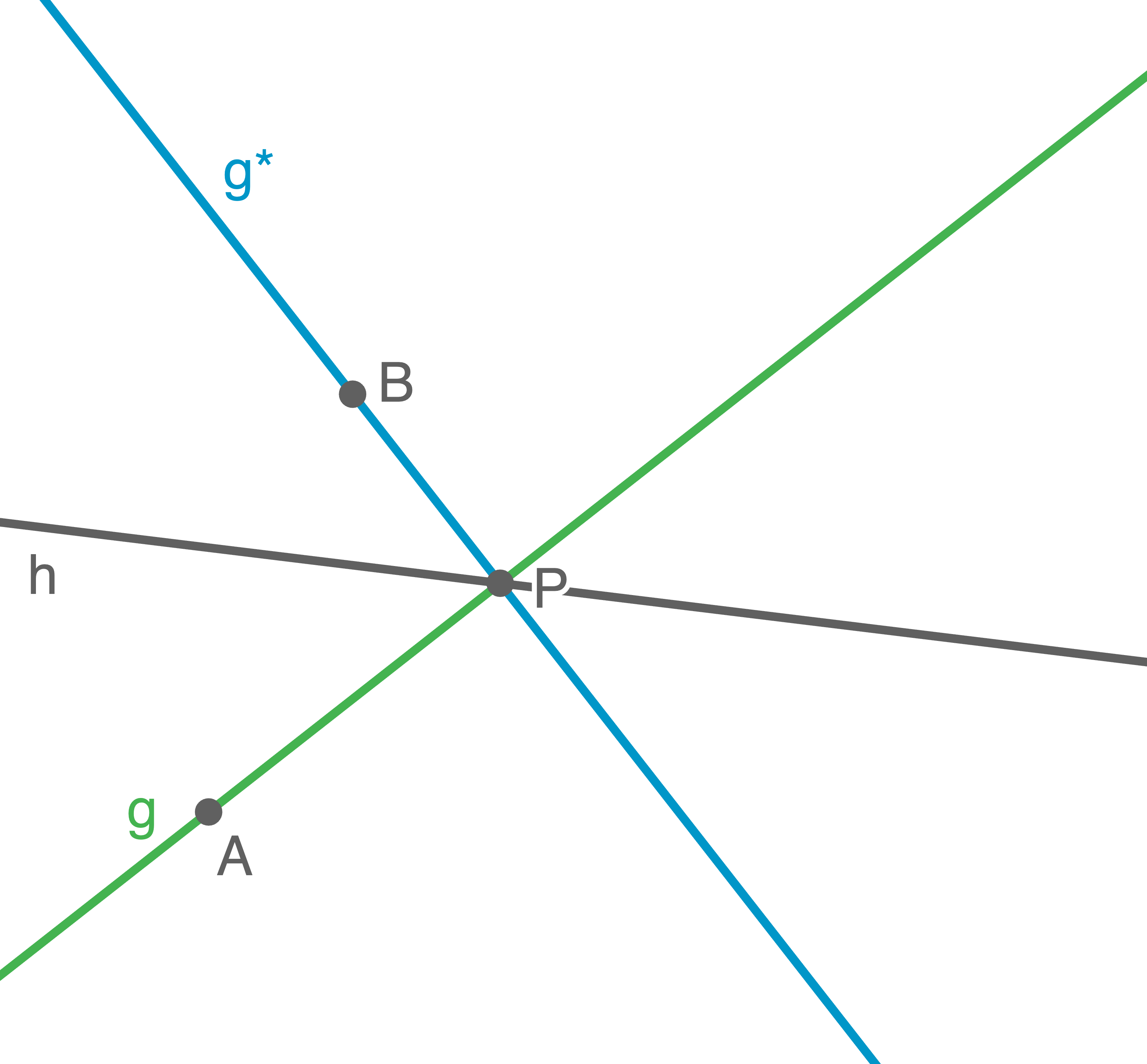 Alternativ kann die Gerade
Alternativ kann die Gerade  auch um
auch um  gedreht durch den Punkt
gedreht durch den Punkt  verlaufen. Mögliche Spiegelachsen sind beide Winkelhalbierenden zwischen den Geraden
verlaufen. Mögliche Spiegelachsen sind beide Winkelhalbierenden zwischen den Geraden  und
und  Term angeben
Term angeben
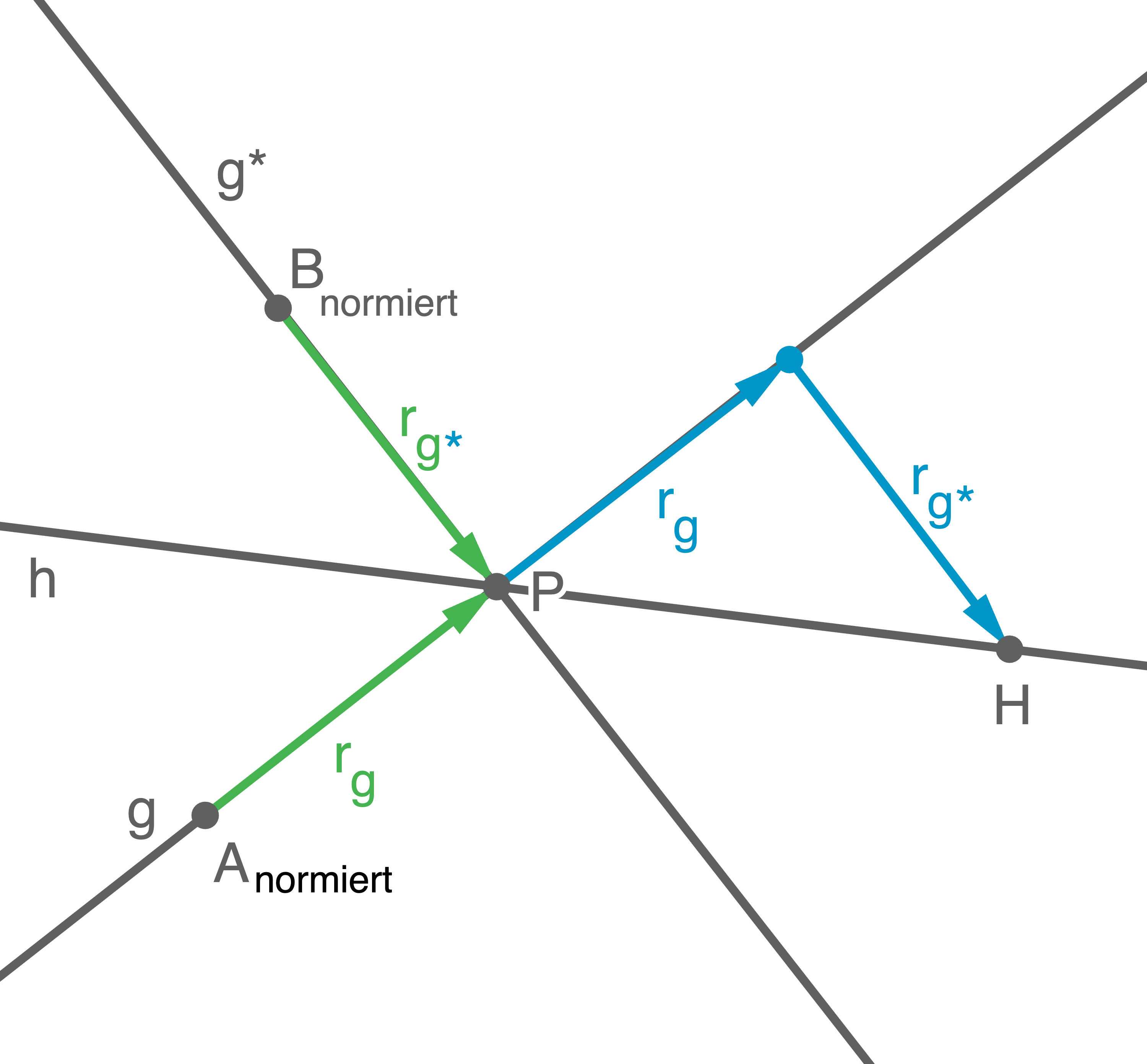

Da die Gerade  den Schnittwinkel halbiert, entspricht ein Richtungsvektor von
den Schnittwinkel halbiert, entspricht ein Richtungsvektor von  der Summe der normierten Richtungsvektoren von
der Summe der normierten Richtungsvektoren von  und
und  Für die normierten Richtungsvektoren gilt:
Für die normierten Richtungsvektoren gilt:
 und
und  Der Ortsvektor eines weiteren Punktes
Der Ortsvektor eines weiteren Punktes  von
von  ergibt sich somit durch:
ergibt sich somit durch:


Hilfsskizze
5.5
a)
Grundgesamtheit: Alle wahlberechtigten Bürger der Stadt.
Stichprobe: Die befragten wahlberechtigten Bewohner des Seniorenheims.
b)
Die Aussage ist nicht zutreffend, da die Stichprobe nicht repäsentativ für die Gesamtwählerschaft ist.
Unterschiede in Alter, sozialem Hintergrund, politischen Einstellungen und anderen demografischen Faktoren zwischen den Bewohnern des Seniorenheims und der gesamten Bevölkerung können zu erheblichen Verzerrungen führen, da die Bewohner eines Seniorenheims in der Regel älter als der Durchschnitt der wahlberechtigten Bevölkerung sind.
Um den aktuellen Stimmenanteil des Kandidaten bei der Oberbürgermeisterwahl realistisch zu schätzen, müsste eine repräsentative Stichprobe erhoben werden, die verschiedene demografische Gruppen der gesamten wahlberechtigten Bevölkerung umfasst. Dies würde eine zufällige Auswahl von Personen aus unterschiedlichen Altersgruppen, sozialen Schichten und geografischen Teilen der Stadt beinhalten.
5.6
Aus dem angegebenen Erwartungswert von 4 ergibt sich für die Summe der drei Zahlen auf den nicht sichtbaren Seiten folgender Wert:
![\(\begin{array}[t]{rll}
E&=& 4& \\[5pt]
\dfrac{1}{6}\cdot (5+5+1+a+b+c)&=& 4&\quad \scriptsize \mid\; \cdot 6\\[5pt]
11+a+b+c&=& 24&\quad \scriptsize \mid\; -11\\[5pt]
a+b+c&=& 13
\end{array}\)](https://mathjax.schullv.de/52b299b5a8a18114800f31f94c6cba0637aa57b6242a5f2e07188ed2e90656b9?color=5a5a5a) Werden diese mit den Zahlen 3, 5 und 5 beschriftet, treffen die ersten zwei Aussagen zu.
Für die Wahrscheinlichkeit des Ereignisses, dass beim zweimaligen Werfen des Würfels zweimal die gleiche Zahl erzielt wird, folgt außerdem:
Werden diese mit den Zahlen 3, 5 und 5 beschriftet, treffen die ersten zwei Aussagen zu.
Für die Wahrscheinlichkeit des Ereignisses, dass beim zweimaligen Werfen des Würfels zweimal die gleiche Zahl erzielt wird, folgt außerdem:
![\(\begin{array}[t]{rll}
P(E)&=& P(5,5)+P(3,3)+P(1,1)& \\[5pt]
&=& \dfrac{4}{6}\cdot \dfrac{4}{6}+\dfrac{1}{6}\cdot \dfrac{1}{6}+\dfrac{1}{6}\cdot \dfrac{1}{6}& \\[5pt]
&=& \dfrac{18}{36}& \\[5pt]
&=& \dfrac{1}{2}
\end{array}\)](https://mathjax.schullv.de/96c7e12a4ffd6bcfbef7b56c40f4dbfcdfea8096f5c784dd6f4e9492dd9b8eb1?color=5a5a5a) Der Würfel kann somit mit den Zahlen 3, 5 und 5 beschriftet werden, sodass er die drei Eigenschaften besitzt.
Der Würfel kann somit mit den Zahlen 3, 5 und 5 beschriftet werden, sodass er die drei Eigenschaften besitzt.