Lerninhalte in Mathe

Abi-Aufgaben eA

Digitales Schulbuch

Inhaltsverzeichnis

Pflichtaufgabe 2 - Analytische Geometrie

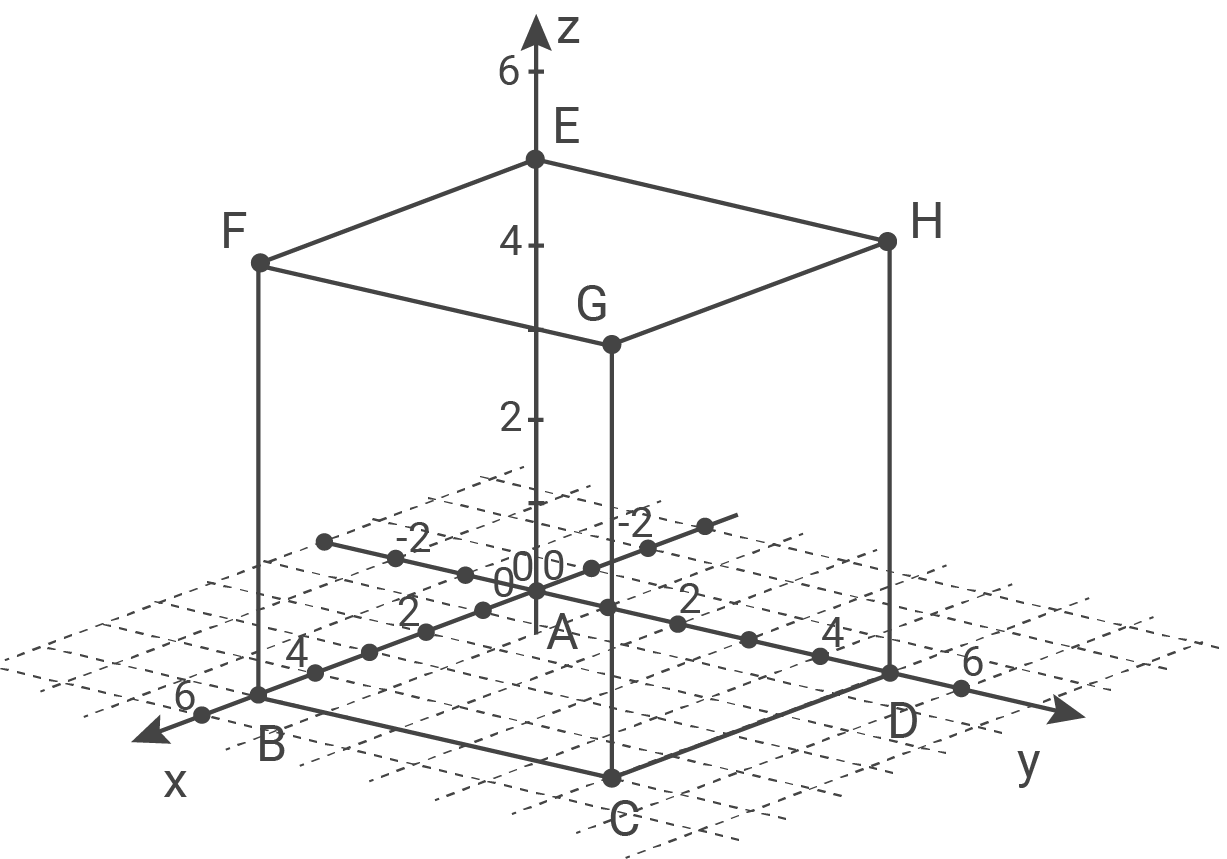
Die Abbildung zeigt den Würfel $ABCDEFGH$ mit $A(0\mid 0\mid 0)$ und $G(5\mid 5 \mid 5)$ in einem kartesischen Koordinatensystem. Die Ebene $T$ schneidet die Kanten des Würfels unter anderem in den Punkten $I(5\mid 0 \mid 1),$ $J(2\mid 5\mid 0),$ $K(0\mid 5\mid 2)$ und $L(1\mid 0\mid 5).$

sachsen anhalt abi ea 2019 aufgabe 2 analytische geometrie abbildung 1

a)

Zeichne das Viereck $IJKL$ in die Abbildung ein.

(2 BE)

b)

Zeige, dass das Viereck $IJKL$ ein Trapez ist, in dem zwei gegenüberliegende Seiten gleich lang sind.

(3 BE)

c)

Ermittle eine Gleichung der Ebene $T$ in Koordinatenform.
(zur Kontrolle: $T: 5x + 4y + 5z-30 = 0$ )

(4 BE)

d)

Spiegelt man $T$ an der Ebene mit der Gleichung $x = 2,5,$ so erhält man die Ebene $\(T$
Zeige, dass $\(T$ durch die Gleichung $-5x + 4y + 5z - 5 = 0$ beschrieben wird. Berechne die Größe des Winkels, unter dem sich $T$ und $\(T$ schneiden.

(6 BE)

e)

Die Spitze einer Pyramide mit der Grundfläche $IJKL$ liegt auf der Strecke $\overline{FG}.$
Untersuche, ob die Höhe dieser Pyramide $2$ sein kann.

(4 BE)

Betrachtet wird die Schar der Geraden $g_a:\overrightarrow{x}=\pmatrix{2,5\\0\\3,5}+r\cdot\pmatrix{0\\-10a\\\dfrac{2}{a}}$ mit $a\in\mathbb{R},$ $a\gt 0,$ $r\in\mathbb{R}.$

f)

Begründe, dass keine Gerade der Schar in der Ebene mit der Gleichung $z = 3,5$ liegt.

(2 BE)

g)

Untersuche, ob die Schnittgerade von $T$ und $\(T$ zur betrachteten Schar gehört.

(4 BE)

a)

Abb. 1: Einzeichnen des Viereck

b)

In der Abbildung von oben kannst du erkennen, dass die beiden parallelen Seiten des Trapezes vermutlich die beiden Seiten $[LI]$ und $[KJ]$ sind. Für die zugehörigen Verbindungsvektoren folgt:

$\begin{array}[t]{rll} \overrightarrow{LI} &=& \pmatrix{4\\0\\-4} \\[5pt] \overrightarrow{KJ} &=& \pmatrix{2\\0\\-2} \end{array}$

Es gilt $\overrightarrow{LI} = 2\cdot \overrightarrow{KJ}.$ Die beiden Vektoren $\overrightarrow{LI}$ und $\overrightarrow{KJ}$ sind also linear abhängig und damit parallel zueinander. Daher sind auch die zugehörigen Vierecksseiten $[LI]$ und $[KJ]$ parallel zueinander. Es handelt sich bei dem Viereck $IJKL$ daher um ein Trapez.
Gefordert ist nun noch zu zeigen, dass die beiden anderen gegenüberliegenden Seiten gleich lang sind. Die Länge der Seiten $[LK]$ und $[IJ]$ kannst du mithilfe des Vektorbetrags berechnen.

$\begin{array}[t]{rll} \overline{LK}&= \sqrt{35} \\[10pt] \overline{IJ}&= \sqrt{35} \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Es ist also $\overline{LK} = \overline{IJ}.$ Die beiden gegenüberliegenden Seiten $[LK]$ und $[IJ]$ sind also gleich lang. Das Viereck $IJKL$ ist also ein Trapez, bei dem zwei gegenüberliegende Seiten gleich lang sind.

c)

Ein Normalenvektor von $T$ kann über das Kreuzprodukt zweier Verbindungsvektoren beispielsweise der drei Punkte $I,$ $J$ und $K$ bestimmt werden:

$\overrightarrow{n} = 2\cdot \pmatrix{5\\4\\5}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für die Ebenengleichung kann nun sowohl der gekürzte Normalenvektor als auch der ursprüngliche verwendet werden. Mit einer Punktprobe mithilfe der Koordinaten eines der vier Punkte folgt:

$d = 30$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Eine Gleichung von $T$ in Koordinatenform lautet:

$T: \,...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

d)

Ebenengleichung

Spiegle zunächst einen Punkt von $T$ an der Ebene mit $x=2,5.$ Die gespiegelte Ebene $T‘$ muss diesen gespiegelten Punkt $P‘$ sowie die Schnittgerade von $T$ und der Ebene mit $x=2,5$ enthalten.

1. Schritt: Einen Punkt von $T$ spiegeln

Betrachte beispielsweise den Punkt $I(5\mid 0\mid 1),$ der in $T$ liegt. Da die Ebene $U$ mit der Gleichung $x=2,5$ parallel zur $yz$ -Ebene verläuft, ändert sich bei einer Spiegelung eines beliebigen Punktes $P$ an dieser Ebene lediglich die $x$ -Koordinate. Die $y$ - und $z$ -Koordinate bleiben gleich.
Der neue Spiegelpunkt $I‘$ muss den gleichen Abstand zur Ebene mit $x=2,5$ besitzen, wie sein Original $I.$ Die $x$ -Koordinate von $I‘$ muss also $x‘ = 0$ sein. Dann haben beide Punkte einen Abstand von $2,5$ zur Ebene mit $x=2,5.$

$I‘(0\mid 0\mid 1).$

2. Schritt: Schnittgerade bestimmen

Bestimme die Schnittgerade von $T$ mit der Ebene, an der gespiegelt werden soll, also mit $x=2,5.$ Setze dazu $x=2,5$ in die Ebenengleichung von $T$ ein:

$4y +5z= 17,5$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Setze nun eine der beiden Koordinaten als Geradenparameter fest, beispielweise $y = t.$ Dann erhältst du:

$z=3,5 - 0,8t$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für die Punkte auf der Schnittgeraden $s$ gilt nun:

$s: ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3. Schritt: Ebenengleichung bestimmen

$T‘$ muss die Gerade $s$ und den Punkt $I‘$ enthalten. Ein Vektor, der die Ebene aufspannt ist daher der Richtungsvektor von $s$ mit $\pmatrix{0\\1\\-0,8}.$ Ein zweiter Spannvektor ist der Verbindungsvektor von $I‘$ und dem Stützpunkt $S$ von $s,$ den du aus der Geradengleichung ablesen kannst $S(2,5\mid 0 \mid 3,5).$

$\overrightarrow{I‘S} = \pmatrix{2,5\\0\\2,5}$

Einen Normalenvektor von $T‘$ kannst du nun über das Kreuzprodukt der beiden Spannvektoren bestimmen:

$\overrightarrow{n}_{T‘} = -0,5\cdot \pmatrix{-5\\4 \\ 5}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da alle Vielfachen von $\pmatrix{2,5 \\ -2 \\ - 2,5 }$ Normalenvektoren von $T‘$ sind, kann man nun entweder den ursprünglichen Vektor $\pmatrix{2,5\\-2\\-2,5}$ oder den erweiterten Vektor $\pmatrix{-5\\4\\5}$ für die Ebenengleichung von $T‘$ verwenden.
Da du zeigen sollst, dass $T‘$ durch die Gleichung $-5x +4y+5z = 5$ beschrieben werden kann, musst du allerdings $\pmatrix{-5\\4\\5}$ verwenden. Die Ebenengleichung von $T‘$ in Koordinatenform hat also folgende Form:

$T‘: \, -5x +4y +5z = d$

Eine Punktprobe mit den Koordinaten von $I‘$ liefert:

$d = 5$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Ebene $T‘$ kann also durch die Gleichung $-5x +4y +5z = 5$ beschrieben werden.

Größe des Schnittwinkels

Die Größe des Schnittwinkels $\alpha$ von $T$ und $T‘$ kannst du mithilfe der Normalenvektoren über die entsprechende Formel berechnen:

$\alpha \approx 76^{\circ}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die beiden Ebenen $T$ und $T‘$ schneiden sich unter einem Winkel der Größe von ca. $76^{\circ}.$

e)

Die Höhe der Pyramide entspricht dem Abstand der Spitze zur Ebene $T.$
Die Spitze liegt auf der Kante $\overline{FG}.$ Diese ist Teil der Geraden durch die beiden Punkte $F$ und $G.$ Die Koordinaten von $F$ kannst du anhand der Koordinaten von $A$ und $G$ zu $F(5\mid 0\mid 5)$ bestimmen. Die Gerade durch $F$ und $G$ kann daher durch folgende Gleichung beschrieben werden:

$\begin{array}[t]{rll} FG:\, \overrightarrow{x} &=& \overrightarrow{OF} + t\cdot \overrightarrow{FG} \\[5pt] &=& \pmatrix{5\\0\\5} + t\cdot \pmatrix{0\\5\\0} \\[5pt] &=& \pmatrix{5\\5t\\5} \\[5pt] \end{array}$

Überprüfe, ob es einen Punkt auf dieser Gerade gibt, der zur Ebene $T$ den Abstand $2$ hat und ob dieser auf der Kante $\overline{FG}$ liegt.

1. Schritt: Punkt mit dem Abstand berechnen

Den Abstand eines Punktes zu einer Ebene kannst du mithilfe der Hesseschen Normalenform darstellen. Für die Hessesche Normalenform von $T$ folgt:

$T:\, \frac{5x +4y +5z -30 }{ \sqrt{66}} = 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Abstand eines Punkts $P(x\mid y\mid z)$ zu $T$ beträgt also:

$d(P,T) = \frac{\left|5x +4y +5z -30\right|}{ \sqrt{66}}$

Einsetzen der Koordinaten der Punkte von $FG$ liefert:

$\left|20+20t \right| = 2\sqrt{66}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Aufgrund des Betrags kann nun $20+20t = 2\sqrt{66}$ und $20+20t = -2\sqrt{66}$ möglich sein:

$\begin{array}[t]{rll} t_1 &=& 0,1\sqrt{66} - 1 \\[5pt] &\approx& -0,19 \\[10pt] t_2 &=& -0,1\sqrt{66} - 1 \\[5pt] &\approx& -1,81 \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2. Schritt: Lage auf der Kante überprüfen

Die Punkte auf der Geraden durch $F$ und $G$ mit der Gleichung $\overrightarrow{x} = \overrightarrow{OF} + t\cdot \overrightarrow{FG}$ liegen für $0\leq t \leq 1$ zwischen den Punkten $F$ und $G,$ also auf der Kante $\overline{FG}.$ Für andere Werte von $t$ liegen die Punkte nicht auf der Kante $\overline{FG}.$ Beide Werte von $t,$ die oben berechnet wurden, sind negativ. Die zugehörigen Punkte mit dem Abstand $2$ zu $T$ liegen nicht auf der Kante $\overline{FG}.$
Die Pyramide kann also nicht die Höhe $2$ besitzen.

f)

Damit eine Gerade in der Ebene mit der Gleichung $z=3,5$ liegt, muss die $z$ -Koordinate jedes Punktes auf dieser Geraden $3,5$ sein. Dazu muss die $z$ -Koordinate des Richtungsvektors Null sein.
Bei der Geradenschar $g_a$ ist die $z$ -Koordinate des Richtungsvektors $\frac{2}{a}.$ Diese kann also in keinem Fall Null werden. Daher liegt keine der Geraden $g_a$ in der Ebene mit der Gleichung $z=3,5.$

g)

Die Schnittgerade von $T$ und $T‘$ ist auch die Schnittgerade von $T$ und der Ebene mit $x=2,5\,,$ an der $T$ gespiegelt wurde. Eine Gleichung dieser Schnittgerade wurde bereits ermittelt:

$s:\, \overrightarrow{x} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Geraden der Schar $g_a$ besitzen folgende Gleichung:

$g_a: \, \overrightarrow{x} = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Durch einen Vergleich der Terme lässt sich feststellen, dass die Stützvektoren von $s$ und $g_a$ in jedem Fall identisch sind. Bleibt noch zu überprüfen, ob es einen Wert von $a$ gibt, für den die Richtungsvektoren linear abhängig sind. Dies ist der Fall, wenn es ein $c\in \mathbb{R}$ gibt, mit:

$\pmatrix{0 \\ 1\\ -0,8} = c\cdot \pmatrix{0 \\ -10a\\ \frac{2}{a}}$

Aus der zweiten Zeile folgt:

$\begin{array}[t]{rll} 1 &=& c\cdot(-10a) &\quad \scriptsize \mid\; :(-10)c \\[5pt] -\frac{0,1}{c} &=& a \end{array}$

Einsetzen in die dritte Gleichung liefert:

$\begin{array}[t]{rll} c_1 &=& -0,2 \\[5pt] c_2 &=& 0,2 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Daraus folgt:

$\begin{array}[t]{rll} a_1 &=& -\frac{0,1}{c_1} \\[5pt] &=& -\frac{0,1}{-0,2} \\[5pt] &=& 0,5\\[10pt] a_2 &=& -\frac{0,1}{c_2} \\[5pt] &=& -\frac{0,1}{0,2} \\[5pt] &=& -0,5\\[10pt] \end{array}$

Da in der Aufgabenstellung $a\in \mathbb{R}^+$ vorgegeben ist, kommt nur $a_1= 0,5$ und $c_1 = -0,2$ infrage. Da der Richtungsvektor von $s$ also linear abhängig zum Richtungsvektor der Geraden $g_{0,5}$ ist und die Stützvektoren beider Geradengleichungen übereinstimmen, beschreibt die Gleichung von $s$ auch die Gerade $g_{0,5}.$ Die Schnittgerade $s$ von $T$ und $T‘$ ist daher eine Gerade der Schar $g_a.$