Pflichtaufgaben

Für jeden Wert von $a\in \mathbb{R} ,$ $a\neq 0,$ ist eine in $\mathbb{R}$ definierte Funktion $f_a$ durch

$f_a(x)= \dfrac{a^2}{3}x^3-2ax^2+4x$ sowie ihre zweite Ableitungsfunktion $\(f_a$ mit

$\(f_a$ gegeben.

Ermittle denjenigen Wert von $a,$ sodass der Graph von $f_a$ durch den Punkt $P(3\mid 3)$ verläuft.

(2 BE)

Der Graph von $f_a$ besitzt für jeden Wert von $a$ einen Wendepunkt.
Weise nach, dass dies ein Wendepunkt mit waagerechter Tangente ist.

(3 BE)

Gegeben ist die in $\mathbb{R}$ definierte Funktion $f$ durch $f(x)=e^{0,5x}.$
In der Abbildung sind der Graph von $f$ sowie der Graph einer linearen Funktion $g$ dargestellt.

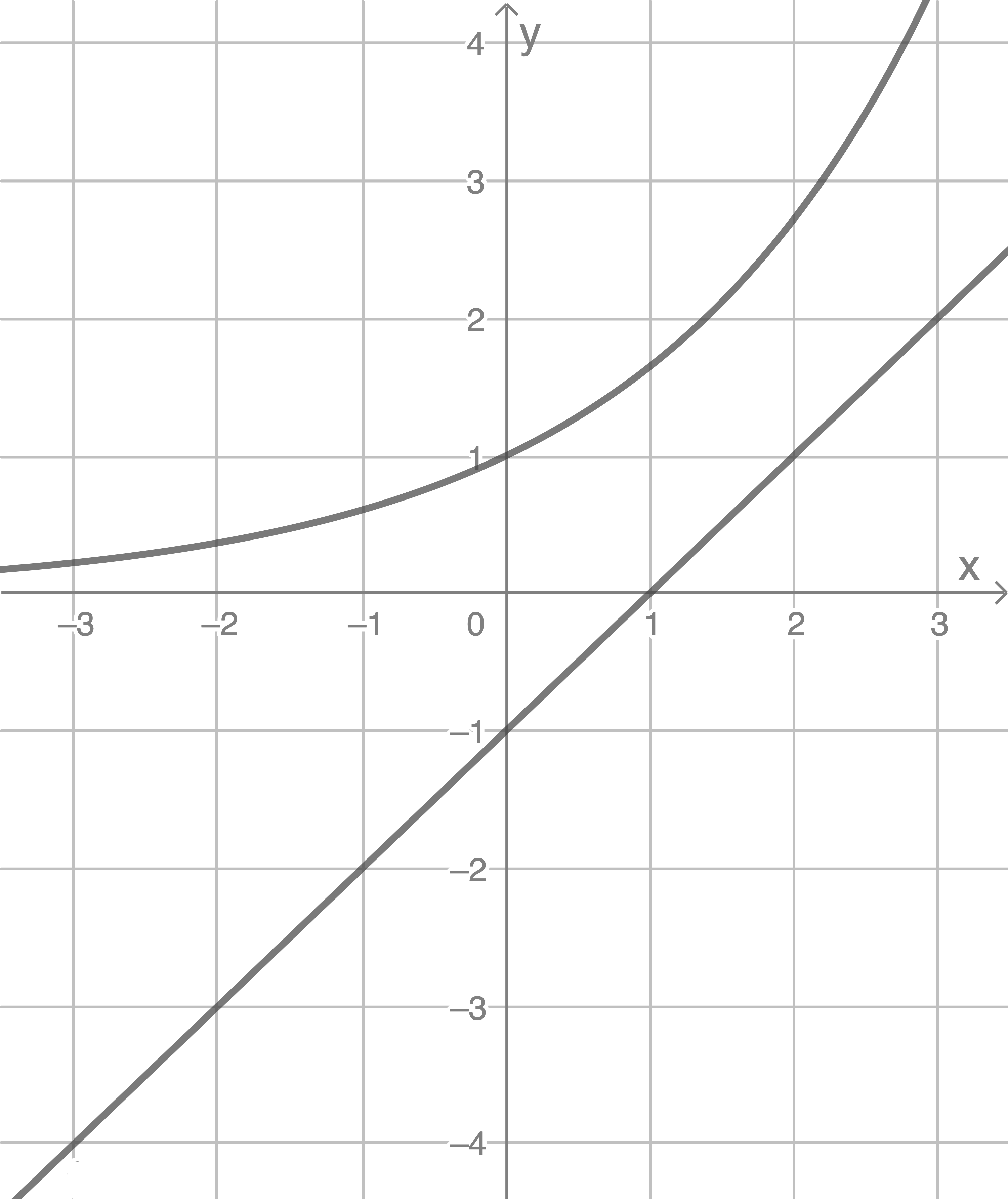
Graph mit zwei Kurven in einem Koordinatensystem. Eine Kurve verläuft exponentiell, die andere linear.

Gib eine Gleichung der Funktion $g$ an.

(1 BE)

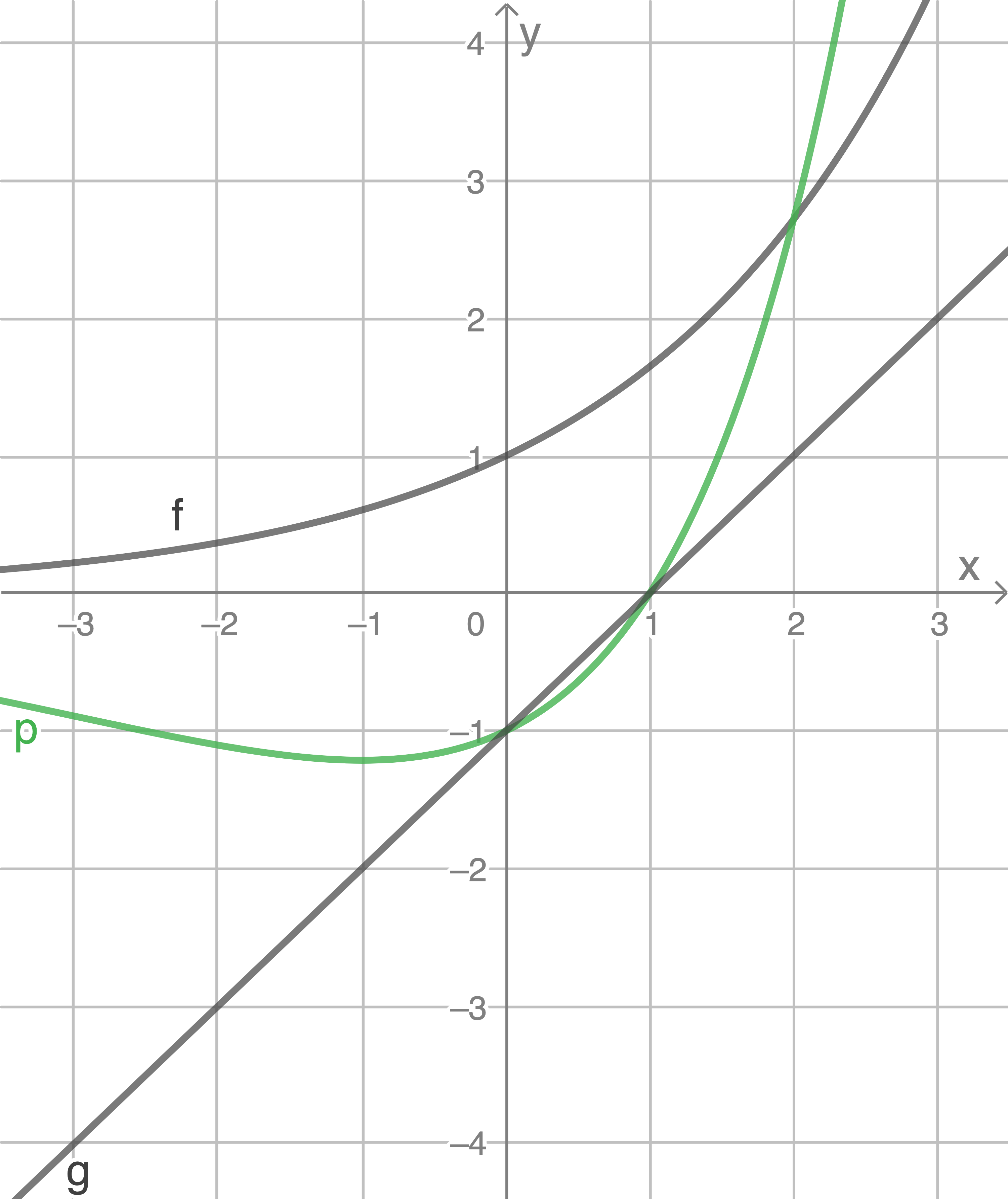
Skizziere den Graphen der Funktion $p$ mit $p(x)=f(x) \cdot g(x)$ im Intervall $-3\leq x \leq 2$ in der Abbildung.

(2 BE)

Begründe, dass die folgende Aussage wahr ist:
„Die Funktion k mit der Gleichung $\(k(x)=f$ besitzt keine Nullstelle.“

(2 BE)

Gegeben sind der Punkt $P(-1 \mid 7 \mid 2)$ und die Ebene $E:x+3y=0.$

Zeige, dass $P$ nicht in $E$ liegt.

(1 BE)

Bestimme die Koordinaten des Punkts, der entsteht, wenn $P$ an $E$ gespiegelt wird.

(4 BE)

Die Zufallsgröße $X$ ist binominalverteilt mt den Parametern $n=100$ und $p$ .
Der Erwartungswert von $X$ ist 50.

Berechne die Standardabweichung von $X$ .

(3 BE)

Die Wahrscheinlichkeit $P(X\geq 61)$ beträgt etwa 2 %. Bestimme damit einen Wert für die Wahrscheinlichkeit $P(40\leq X \leq 60).$

(2 BE)

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?

Vollständigen Rechenweg anzeigen

$a=1$

Für $a=1$ verläuft der Graph von $f_a$ durch den Punkt $P(3\mid 3).$

1. Wendestelle mit dem notwendigen Kriterium bestimmen

Vollständigen Rechenweg anzeigen

$x=\frac{2}{a}$

2. Steigung des Graphen in der Wendestelle bestimmen

Vollständigen Rechenweg anzeigen

$\( f_a$

Die Tangente an den Graphen von $f_a$ im Wendepunkt ist also waagerecht.

Aus der Abbildung lässt sich für die Gerade die Steigung $1$ sowie der $y$ -Achsenabschnitt $-1$ ablesen:

$g(x)= x-1$

Graph mit zwei Funktionen, dargestellt in verschiedenen Farben auf einem Koordinatensystem.

Wegen des Satzes vom Nullprodukt, ist $\(f$ wenn $\(f$ oder $\(g$ ist.

$\(f$

$\(g$

Also besitzt $k$ keine Nullstelle.

Koordinaten von $P$ in die Gleichung von $E$ einsetzen:

$-1+ 3\cdot 7 = 20 \neq 0$

Der Punkt $P$ liegt also nicht in $E.$

1. Aufstellen einer zu $E$ orthogonalen Gerade durch $P$

$g:\, \overrightarrow{x} = \pmatrix{-1\\7\\2} + r\cdot \pmatrix{1\\3\\0}$

2. $g$ in $E$ einsetzen

Vollständigen Rechenweg anzeigen

$r=-2$

3. Spiegelpunkt bestimmen

$\(\overrightarrow{OP$ $= \pmatrix{-1\\7\\2} +2\cdot (-2)\cdot \pmatrix{1\\3\\0}$ $= \pmatrix{-5\\-5\\2}$

Wenn $P$ an $E$ gespiegelt wird, entsteht der Punkt $\(P$ mit den Koordinaten $\(P$

$p$ mit der Formel für den Erwartungswert berechnen:

$\begin{array}[t]{rll} \mu &=& n\cdot p \\[5pt] 50 &=& 100 \cdot p &\quad \scriptsize \mid\;:100 \\[5pt] 0,5 &=& p \end{array}$

Für die Standardabweichung folgt:

$\sigma = \sqrt{100\cdot 0,5 \cdot 0,5} = 5$

Da $X$ binomialverteilt mit $p=0,5$ und $\mu=50$ ist, gilt $P(X\leq 39) = P(X\geq 61).$ Damit folgt:

$P(40\leq X\leq 60)$ $= 1- 2\cdot P(X\geq 61)$ $\approx 1-2\cdot 0,002 = 0,96.$

Weiter lernen mit SchulLV-PLUS!

monatlich kündbarSchulLV-PLUS-Vorteile im ÜberblickDu hast bereits einen Account?