Lerninhalte in Mathe

Abi-Aufgaben eA

Digitales Schulbuch

Inhaltsverzeichnis

Pflichtaufgabe 1 - Analysis

1.1

Für jeden Wert von $k\in \mathbb{R},$ $k\gt 0,$ ist eine in $\mathbb{R}$ definierte Funktion $f_k$ mit $f_k(x)=8k\cdot(kx-1)^2\cdot(kx+1)^2$ festgelegt. Der Graph von $f_k$ wird mit $G_k$ bezeichnet.

a)

Berechne die Koordinaten der Punkte, die $G_k$ mit den Koordinatenachsen gemeinsam hat.

(3 BE)

b)

Skaliere in der Abbildung 1 die beiden Achsen so, dass die gezeigte Kurve den Graphen $G_{\frac{1}{4}}$ darstellt.

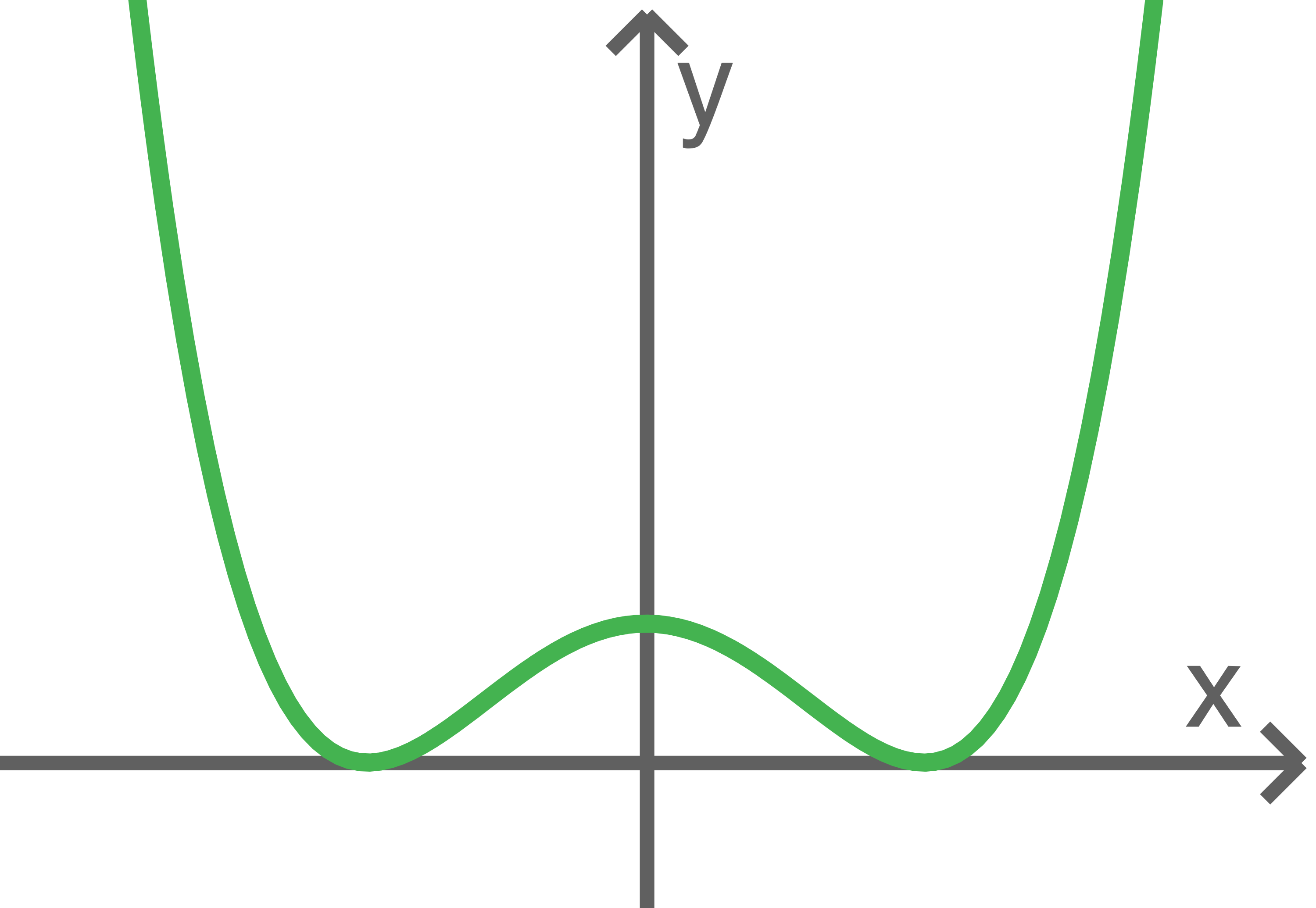
sachsen anhalt abi ea 2019 aufgabe 1 analysis abbildung 1 funktion fk

Abbildung 1

(2 BE)

c)

Beschreibe, wie der Graph $G_{2k}$ aus $G_k$ hervorgeht.

(2 BE)

$G_k$ schließt im ersten Quadranten mit den Koordinatenachsen ein Flächenstück ein. Die Abbildung 2 zeigt dieses Flächenstück (grün markiert) sowie das Rechteck mit den Eckpunkten $\left(0\mid f_k(0)\right)$ und $\left(\dfrac{1}{k}\mid 0\right),$ dessen Seiten parallel zu den Koordinatenachsen sind.

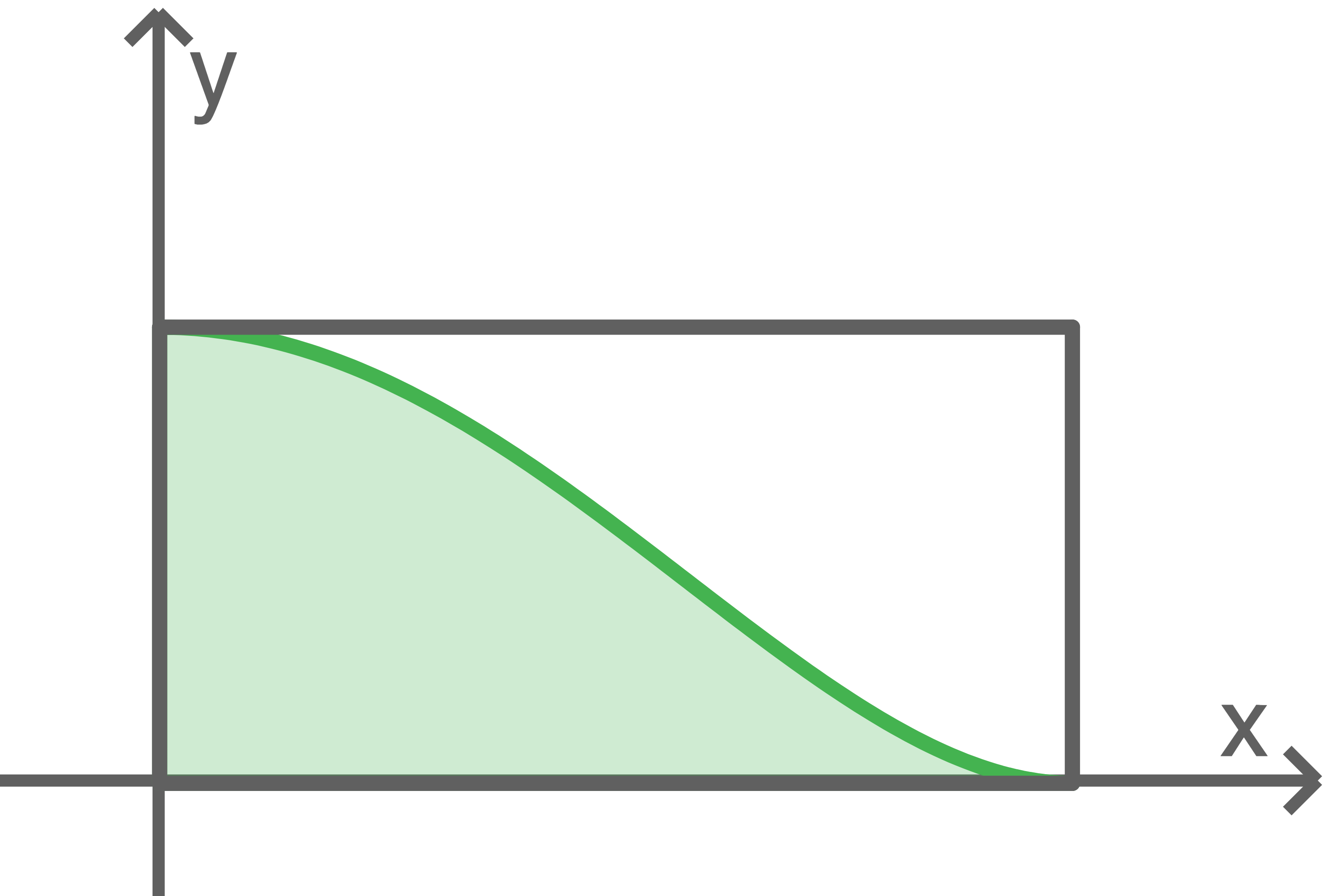
sachsen anhalt abi ea 2019 aufgabe 1 analysis abbildung 2

Abbildung 2

d)

Es gilt $f_k(x)=8k\cdot(k^2x^2-1)^2.$
Berechne den Inhalt des Flächenstücks.

(4 BE)

Bei Rotation des Rechtecks um die $x$ -Achse entsteht ein Körper, ebenso bei Rotation um die $y$ -Achse.

e)

Skizziere einen der beiden Körper und beschrifte die Skizze mit den Maßen des Körpers.

(2 BE)

f)

Ermittle denjenigen Wert von $k,$ für den die beiden Körper das gleiche Volumen haben.

(3 BE)

g)

Bei Rotation des grün markierten Flächenstücks um die $y$ -Achse entsteht ein weiterer Körper. Begründe, dass das Volumen dieses Körpers mit zunehmendem Wert von $k$ beliebig klein wird.

(5 BE)

1.2

Im Folgenden werden die in $\mathbb{R}$ definierten Funktionen $f$ und $g$ mit

$f(x)= \dfrac{1}{4}x^4-2x^2+4$ und $g(x)=(x-2)^2\cdot\mathrm e^x$

betrachtet.

a)

Die Funktion $f$ ist eine Funktion der Schar aus Aufgabe 1.1.
Ermittle den zugehörigen Wert von $k.$

(2 BE)

b)

Zwei Extrempunkte des Graphen von $f$ liegen auf dem Graphen von $g.$
Berechne die Koordinaten dieser Punkte.

(4 BE)

c)

Die Abbildung 3 zeigt die Graphen von $f$ und $g$ für $0\leq x\leq 2.$
Ordne jeden der Graphen I und II der passenden Funktion zu und begründe deine Zuordnung.

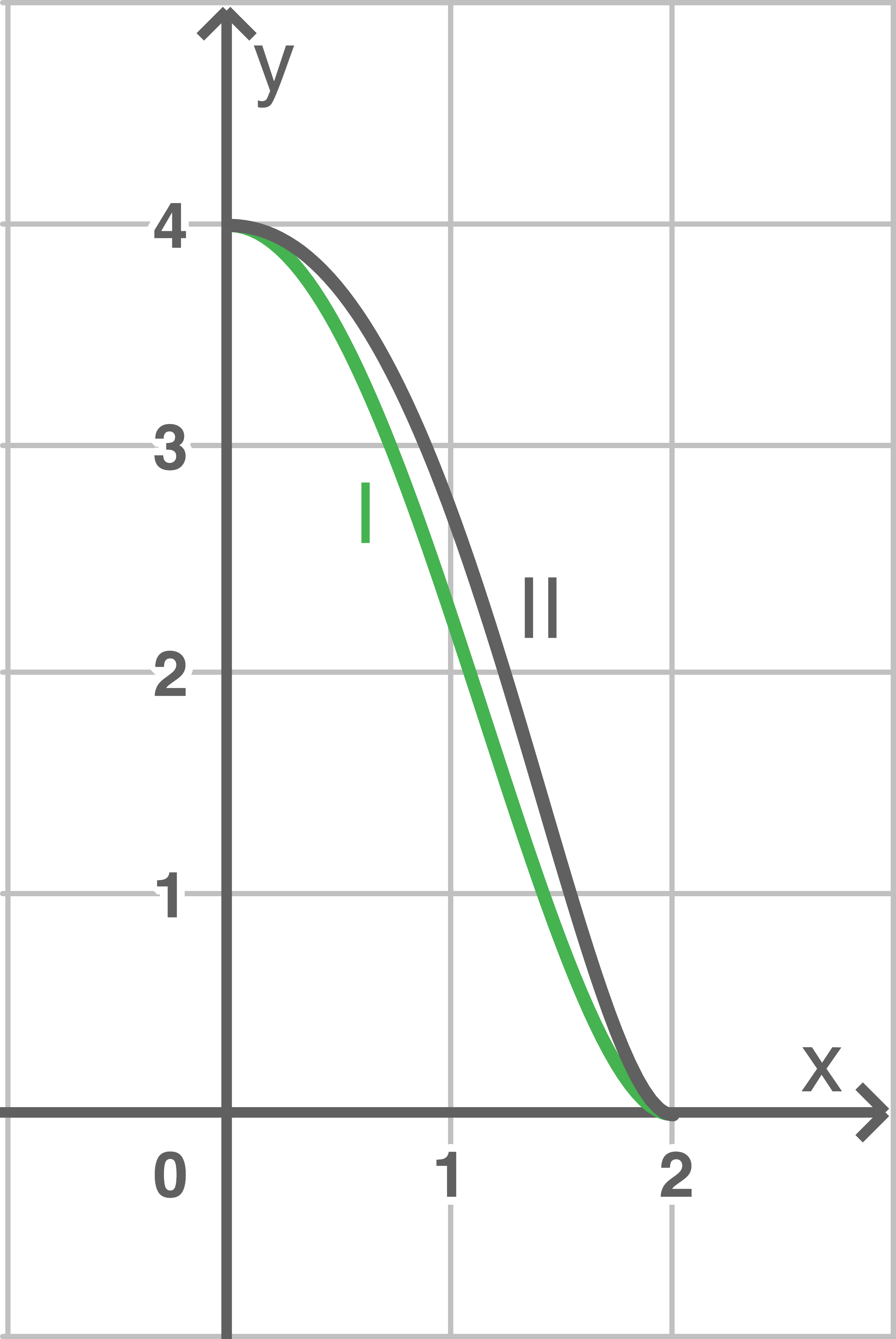
sachsen anhalt abi ea 2019 aufgabe 1 analysis abbildung 3 funktion f g

Abbildung 3

(2 BE)

d)

Betrachtet wird die Tangente an den Graphen von $g$ im Punkt $P(p\mid g(p))$ mit $0\lt p\lt 2.$ Ermittle rechnerisch denjenigen Wert von $p,$ für den diese Tangente die $x$ -Achse im Punkt $Q(2\mid 0)$ schneidet.

(6 BE)

1.1

a)

Schnittpunkt mit der $y$ -Achse:

$f_k(0)=8k$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Graphen von $f_k$ schneiden die $y$ -Achse in den Punkten $S_{y_k}(0\mid 8k).$

Schnittpunkt mit der $x$ -Achse:

$(kx-1)^2\cdot(kx+1)^2 = 0$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Mit dem Satz vom Nullprodukt ist das der Fall, wenn:

$\begin{array}[t]{rll} \text{I}\quad x_1 &=& \frac{1}{k} \\[10pt] \text{II}\quad x_2 &=& -\frac{1}{k} \\[10pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Die Graphen von $f_k$ schneiden die $x$ -Achse jeweils in den Punkten $S_{x_{k_1}}\left(\frac{1}{k}\mid 0\right)$ und $S_{x_{k_2}}\left(-\frac{1}{k}\mid 0\right).$

$\,$

b)

Abb. 1

$\,$

c)

$f_{2k}(x) = 2\cdot f_k(2x)$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Durch den Faktor $2$ direkt vor dem $x$ findet im Graphen eine Stauchung in $x$ -Richtung um den Faktor $2$ statt. Durch den Faktor $2$ vor dem Funktionsterm findet eine Streckung in $y$ -Richtung statt. Der Graph von $G_{2k}$ geht aus dem Graphen von $G_k$ also durch eine Stauchung in $x$ -Richtung um den Faktor $2$ und eine anschließende Streckung in $y$ -Richtung um den Faktor $2$ hervor.

$\,$

d)

$F=\frac{64}{15}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Inhalt des Flächenstücks beträgt $\frac{64}{15}$ Flächeneinheiten.

$\,$

e)

$\blacktriangleright$ Lösungsweg A: Rotation um die $x$ -Achse

$Rotation um die <img alt = '\(x\)' class='mathjax-formula' src='https://mathjax.schullv.de/2d711642b726b04401627ca9fbac32f5c8530fb1903cc4db02258717921a4881?color=5a5a5a'/>-Achse$

Abb. 3: Rotation um die $x$ -Achse

$\blacktriangleright$ Lösungsweg B: Rotation um die $y$ -Achse

$Rotation um die <img alt = '\(y\)' class='mathjax-formula' src='https://mathjax.schullv.de/a1fce4363854ff888cff4b8e7875d600c2682390412a8cf79b37d0b11148b0fa?color=5a5a5a'/>-Achse$

Abb. 4: Rotation um die $y$ -Achse

$\,$

f)

Bei der Rotation des Rechtecks um eine der Achsen entsteht ein Zylinder. Das Volumen eines Zylinders hängt von seiner Höhe und seinem Radius ab. Für beide möglichen Zylinder sind diese beiden Größen in der jeweiligen Abbildung eingetragen.
Bei der Rotation um die $x$ -Achse gilt:

$V_x=64\pi\cdot k$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für die Rotation um die $y$ -Achse gilt:

$V_y =\frac{8\pi}{k}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Beide Volumina sollen nun gleich groß sein:

$k=\frac{1}{\sqrt{8}}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für $k= \frac{1}{\sqrt{8}}$ haben beide Körper das gleiche Volumen.

$\,$

g)

Die graumarkierte Fläche liegt in jedem Fall in dem zugehörigen Rechteck. Das Volumen des Körpers, der durch Rotation des Rechtecks um die $y$ -Achse entsteht, kann laut Aufgabenteil 1 e) wie folgt berechnet werden:

$V_y = \frac{8\pi}{k}$

Für $k\to \infty$ gilt für das Volumen des Körpers, der durch Rotation des Rechtecks um die $y$ -Achse entsteht:

$V_y = \frac{8\pi}{k} \to 0$

Das Volumen des Rotationskörpers, der durch die Rotation des Rechtecks um die $y$ -Achse entsteht, wird mit zunehmendem Wert von $k$ also beliebig klein. Da die grau markierte Fläche innerhalb des Rechtecks liegt und dadurch kleiner als das Rechteck ist, gilt dies also auch für das Volumen des Rotationskörpers, der bei Rotation der grau markierten Fläche um die $y$ -Achse entsteht.

1.2

a)

$... = ...$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Durch einen Vergleich der Koeffizienten erhältst du beispielsweise:

$k=\frac{1}{2}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Da in der Aufgabenstellung angegeben ist, dass $f$ eine Funktion der Schar $f_k$ ist, musst du die übrigen Koeffzienten nicht überprüfen. Es ist also $f= f_{k}$ mit $k = \frac{1}{2}.$

$\,$

b)

1. Schritt: Ableitungsfunktion bestimmen

$f‘(x) = x^3 -4x$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

2. Schritt: Notwendiges Kriterium für Extremstellen anwenden

$\begin{array}[t]{rll} x_1 &=& 0 \\[5pt] x_2 &=& -2 \\[5pt] x_3 &=& 2 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

3. Schritt: Zugehörige Funktionswerte überprüfen

$\begin{array}[t]{rll} f(0) &=& 4 \\[10pt] f(-2)&=& 0 \\[10pt] f(2) &=& 0 \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

4. Schritt: Funktionswerte von $g$ berechnen

$\begin{array}[t]{rll} g(0) &=& 4 \\[10pt] g(-2)&=& 16\mathrm e^{-2} \\[10pt] f(2) &=& 0 \\[5pt] \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

An den beiden möglichen Extremstellen $x_1 = 0$ und $x_3 = 2$ stimmen die Funktionswerte von $f$ und $g$ überein. Die Koordinaten der beiden Extrempunkte des Graphen von $f,$ die auf dem Graphen von $g$ liegen lauten also $E_1(0\mid 4)$ und $E_2(2\mid 0).$

$\,$

c)

$\begin{array}[t]{rll} f(1) &=& 2,25 \\[10pt] g(1) &\approx& 2,72 \end{array}$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Der Funktionswert von $g$ an der Stelle $x=1$ ist also größer als der von $f.$ Graph $\text{II}$ gehört daher zur Funktion $g$ und Graph $\text{I}$ gehört zu $f.$

$\,$

d)

Die gesuchte Tangente $t$ soll durch den Punkt $P(p\mid g(p))$ und den Punkt $Q(2\mid 0)$ verlaufen. Ihre Steigung kann also in Abhängigkeit von $p$ mithilfe des Differenzenquotienten wie folgt dargestellt werden:

$m_t = (p-2)\cdot \mathrm e^p$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Zudem soll $t$ eine Tangente an den Graphen von $g$ an der Stelle $p$ sein. Also muss für die Steigung zusätzlich gelten:

$m_t = g‘(p)$

Mithilfe der Produktregel und der Kettenregel erhältst du:

$g‘(x) =x\cdot (x-2)\cdot \mathrm e^x$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Es ist also auch:

$m_t = g‘(p)= p\cdot (p-2)\cdot \mathrm e^p$

Beides kannst du nun gleichsetzen:

$p = 1$

Grüne Lupe mit einem Pluszeichen, Symbol für Vergrößerung oder Detailansicht.

Vollständige Lösung anzeigen

Für den Wert $p=1$ schneidet die Tangente an den Graphen von $g$ im Punkt $P(p\mid g(p))$ die $x$ -Achse im Punkt $Q(2\mid 0).$