Wahlpflichtaufgabe 2 - Analytische Geometrie

4.2

Im kartesischen Koordinatensystem werden das Dreieck $ABC$ , der Kreis $k_1$ und der Kreis $k_2$ mit $x^2+y^2-2(x+y)=15$ betrachtet.
Der Kreis $k_1$ ist der Inkreis des Dreiecks $ABC$ und er berührt

die Seite $\overline{AB}$ im Punkt $D(0\mid5)$
die Seite $\overline{BC}$ im Punkt $E(-3\mid-4)$
die Seite $\overline{AC}$ im Punkt $F(5\mid0)$

Zeige, dass der Mittelpunkt von $k_1$ im Koordinatenursprung $O$ liegt und gib eine Gleichung des Kreises $k_1$ an.

(3 BE)

Zeichne das Dreieck $ABC$ in das abgebildete Koordinatensystem ein und begründe, dass das Dreieck $ABC$ rechtwinklig ist.

(zur Kontrolle: $C(5\mid-10)$ )

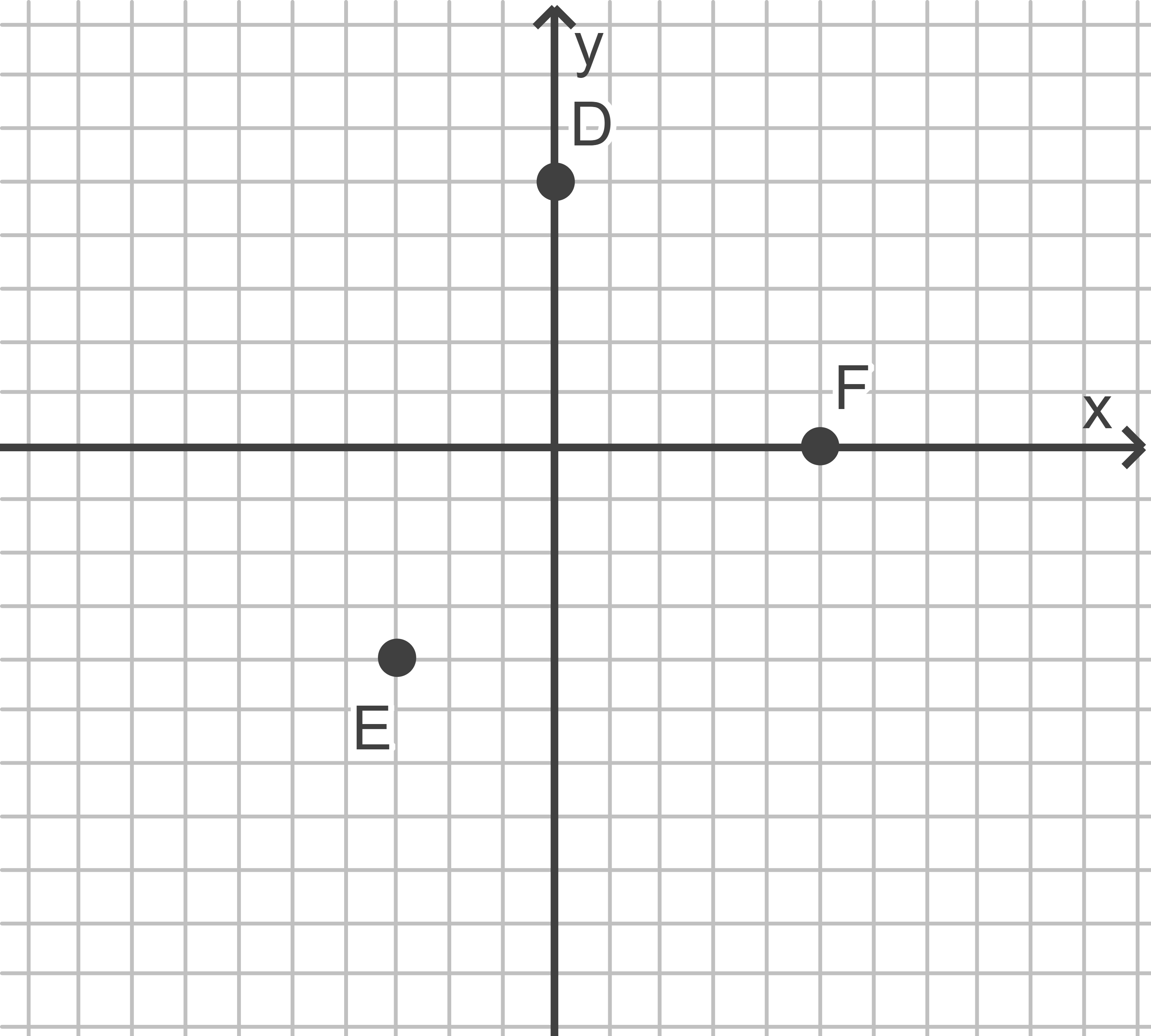
Koordinatensystem mit Punkten E, D und F auf den Achsen x und y.

(3 BE)

Entscheide, ob das Viereck aus den Punkten $C,$ $E,$ $F$ und $O$ einen Umkreis besitzt.
Begründe deine Entscheidung.

(3 BE)

Ermittle die Koordinaten des Mittelpunktes des Kreises $k_2$ .

(2 BE)

Betrachtet wird das Gleichungssystem mit dem Lösungsansatz

$\begin{array}{lrll} \text{I:}\quad&x^2+y^2&=& 25 &\quad \scriptsize\\ \text{II:}\quad&x^2+y^2-2(x+y)&=& 15&\quad \\ \hline \text{I-II:}\quad&2(x+y)&=& 10 & \end{array}$

Deute die Gleichung $2(x+y)=10$ in Bezug auf die durch die Gleichungen $\text{I}$ und $\text{II}$ beschriebenen Objekte und löse das Gleichungssystem.

(4 BE)

4.2

O ist der Mittelpunkt des Kreises, wenn alle Punkte, die auf dem Kreisrand liegen den gleichen Abstand zum Ursprung O haben.

Punkt F:
$d=5$

Punkt D:
$d=5$

Punkt E:
$d=\sqrt{3^2 + 4^2}=5$

Da die Punkte auf dem Kreisrand alle den Abstand 5 vom Koordinatenursprung O haben, ist O gleichzeitig der Mittelpunkt des Kreises.

Die Kreisgleichung kannst du mit $r=5$ erstellen: $x^2+y^2=25$

Grafik eines Koordinatensystems mit einer grünen Kreislinie und mehreren markierten Punkten.

Das Dreieck ABC ist rechtwinklig, da der Punkt $D$ auf der y-Achse liegt und die Seite $\overline{AB}$ deshalb orthogonal zur y-Achse und somit parallel zur x-Achse verläuft.
Da der Punkt $F$ auf der x-Achse liegt, ist die Seite $\overline{AC}$ orthogonal zur x-Achse und parallel zur y-Achse. Insgesamt schließen die Seiten $\overline{AB}$ und $\overline{AC}$ einen rechten Winkel ein.

Ein Viereck besitzt einen Umkreis, wenn sich alle Mittelsenkrechten der Seiten in einem Punkt schneiden, welcher dann der Mittelpunkt des Kreises ist.

Das Viereck CEFO hat die Form eines Drachens. Bei diesem Drachen schneiden sich die Mittelsenkrechten in einem Punkt, weil die beiden Winkel, die nicht an der Symmetrieachse liegen rechte Winkel sind.
Aus diesem Grund ist der Mittelpunkt des Umkreises der Schnittpunkt der Mittelsenkrechten.

Die zweite Kreisgleichung lautet $k_2 :x^2+y^2-2(x+y)=15$ .
Die allgemeine Kreisgleichung lautet $(x-m_1)^2 +(y-m_2)^2 =r^2$ , dabei sind $m_1$ und $m_2$ die Koordinaten des Mittelpunktes $M(m_1 \mid m_2)$ . Bringe nun die allgemeine Kreisgleichung auf die Form von $k_2$ .

$(x-m_1)^2 +(y-m_2)^2 =r^2$

$\begin{array}[t]{rll} x^2 -2x\cdot m_1 +m_1^2 +y^2-2y \cdot m_2 +y_m^2&=& r^2&\quad \scriptsize \\[5pt] x^2 +y^2 -2x\cdot m_1-2y\cdot m_2 +m_1^2 +m_2^2 &=& r^2&\quad \scriptsize \\[5pt] \end{array}$

Du siehst nun, dass du die Gleichung nur auf die Form von $k_2$ bringen kannst, indem du Werte für $m_1$ und $m_2$ einsetzt.

Du siehst, dass du nur mit $m_1=1$ und $m_2=1$ von $-2x\cdot m_1-2y\cdot m_2$ auf $-2(x+y)$ kommst.

Somit ergibt sich

$\begin{array}[t]{rll} x^2 +y^2 -2x\cdot 1 -2y\cdot 1 +2 &=&r^2 &\quad \scriptsize \mid\;-2 \\[5pt] x^2+y^2 -2(x+y)&=&r^2-2 \end{array}$

Diese Gleichung entspricht der Kreisgleichung $k_2$ . Somit lauten die Koordinaten des Kreises $k_2$ $M(1 \mid 1).$

Mit dem Gleichungssystem wird berechnet in welchen Punkten sich die Kreise $k_1$ und $k_2$ schneiden. Im ersten Schritt werden die beiden Kreisgleichungen subtrahiert. Das Ergebnis ist die Gleichung $2(x+y)=10$ .
Es müssen nun $x$ und $y$ ermittelt werden.

Löse $2(x+y)=10$ nach einer Variablen auf und setze diese in die beiden Gleichungen ein:

$\begin{array}[t]{rll} 2x+2y&=& 10&\quad \scriptsize \mid -2y \, \mid :2\; \\[5pt] x&=&5-y \end{array}$

$x$ in $\text{I}$ :
$\begin{array}[t]{rll} (5-y)^2+y^2&=& 25&\quad \scriptsize \; \\[5pt] 25-10y+y^2+y^2&=& 25&\quad \scriptsize \mid \;-25 \\[5pt] -10y+2y^2&=& 0&\quad \scriptsize \mid\;\text{ausklammern} \\[5pt] y( -10 +2y)&=& 0&\quad \scriptsize \; \\[5pt] \end{array}$

Somit ergeben sich die Lösungen für $y$ mit $y_1=0$ und $y_2= \dfrac{10}{2}=5.$
Berechne die zugehörigen x-Werte: $x_1=5-5=0$ und $x_2= 5-0=5$

Die Kreise schneiden sich in $(0|5)$ und in $(5 |0)$ .