 Nullstellen der Funktion
Nullstellen der Funktion  berechnen
berechnen
In dieser Aufgabe sollst du die Nullstellen der Funktion

berechnen. Gesucht sind also die

-Werte, für die

ist. Dazu kannst du den Satz vom Nullprodukt verwenden.
Ein Produkt ist genau dann Null, wenn einer der Faktoren Null ist.
Löse also die beiden Gleichungen

und

nach

auf.
![\(\begin{array}[t]{rll}
b^2-x^2&=&0 &\quad \scriptsize \mid\; +x^2 \mid\;\sqrt\; \\[5pt]
x_1&=&-b \\[5pt]
x_2&=& b
\end{array}\)](https://mathjax.schullv.de/834133638e7d56b0a37e77a3b514d49a9abb683b58e3727ab4d8f8bd136898ad?color=5a5a5a)
![\(\begin{array}[t]{rll}
b+x&=&0 &\quad \scriptsize \mid\;-b \\[5pt]
x_3&=&-b
\end{array}\)](https://mathjax.schullv.de/f8386b31b3c998d84690d5413915fc154e29f2eeff8a1b80b98917ba1ef4e8a9?color=5a5a5a)

hat zwei Nullstellen

und

. Die Nullstelle

ist eine doppelte Nullstelle.
 Verhalten der Funktion
Verhalten der Funktion  für
für  untersuchen
untersuchen
Am einfachsten ist es, wenn du als erstes den Funktionsterm ausmultiplizierst und anschließend das Verhalten der Funktion

für

betrachtest.
Bei dem Term innerhalb der Klammer handelt es sich um den Funktionsterm einer ganzrationalen Funktion vierten Grades. Eine ganzrationale Funktion vierten Grades strebt gegen

wenn

. Da die Klammer aber ein negatives Vorzeichen hat, bedeutet das:

 Extrempunkte nachweisen
Extrempunkte nachweisen
In dieser Aufgabe sollst du nachweisen, dass die Punkte

die Extrempunkte des Graphen von

sind.
Du hast die Funktion

gegeben und sollst deren Graph auf
Extrempunkte untersuchen. Für eine Extremstelle

benötigst du die beiden folgenden Kriterien:
- Notwendiges Kriterium:

- Hinreichendes Kriterium:
- Ist
 , handelt es sich um eine Minimalstelle.
, handelt es sich um eine Minimalstelle.
- Ist
 , handelt es sich um eine Maximalstelle.
, handelt es sich um eine Maximalstelle.
Du kannst also wie folgt vorgehen:
- Bestimme die ersten beiden Ableitungsfunktionen
 und
und  .
.
- Wende das notwendige Kriterium an, indem du
 setzt und nach
setzt und nach  löst.
löst.
- Überprüfe das hinreichende Kriterium, indem du die Lösung aus 2. in
 einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
1. Schritt: Ableitungsfunktionen bestimmen
![\(\begin{array}[t]{rll}
f_b(x)&=&-x^4-2x^3b+2xb^3+b^4 \\[10pt]
f‘_b(x)&=& -4x^3-6x^2b+2b^3\\[10pt]
f‘‘_b(x)&=& -12x^2-12bx
\end{array}\)](https://mathjax.schullv.de/799e1859f7542270722c150494cb09ce3673af492b66105c912454f0f2f9fcb2?color=5a5a5a) 2. Schritt: Notwendiges Kriterium anwenden
2. Schritt: Notwendiges Kriterium anwenden
Durch Gleichsetzen von

mit Null, erhältst du mögliche Extremstellen:
Um die Nullstellen zu berechnen, musst du als erstes eine Nullstelle durch probieren bestimmen und dann mit der Polynomdivision auf die anderen Nullstellen schließen. Eine Nullstelle ist

. Teile somit den Funktionsterm durch

.
Du kannst nun die

-

-Formel anwenden, um die weiteren Nullstellen zu bestimmen.
![\(\begin{array}[t]{rll}
0& =&-4x^2-2bx+2b^2 & \quad \mid\; :(-4) \\[5pt]
0& =&x^2+\frac{1}{2}bx - \frac{1}{2}b^2 \\[5pt]
x_{2,3}&=&- \dfrac{\frac{1}{2}b}{2} \pm \sqrt {\left( {\frac{\frac{1}{2}b}{2}} \right)^2 + \frac{1}{2}b^2} \\[5pt]
&=& -\frac{1}{4}b \pm \sqrt {{\frac{1}{16}b^2} + \frac{8}{16}b^2} \\[5pt]
&=& -\frac{1}{4}b \pm \frac{3}{4}b\\[5pt]
x_1&=& -\frac{1}{4}b + \frac{3}{4}b\\[5pt]
&=& \frac{1}{2}b \\[5pt]
x_2&=& -\frac{1}{4}b - \frac{3}{4}b\\[5pt]
&=& -\frac{1}{4}b \pm \frac{3}{4}b\\[5pt]
\end{array}\)](https://mathjax.schullv.de/d242b55356da0c29b7de921f15f6dfca4b78a06fb968a346f4cdb93af3d98a7e?color=5a5a5a)
Zwei weitere Stellen, an denen Extrempunkte sein könnten sind

und

. Wobei es sich an der Stelle

um eine doppelte Nullstelle handelt.
3. Schritt: Hinreichendes Kriterium überprüfen
Um nun zu prüfen, ob es sich tatsächlich um Extremstellen handelt, bestimmst du die zweite Ableitungsfunktion und setzt die möglichen Werte für

in den Funktionsterm ein. Ist

handelt es sich um keine Extremstelle.

 da
da 
Da der Graph der Funktion an der Stelle

keinen Extrempunkt besitzt, sind alle möglichen Extrempunkte im Punkt

. Da die zweite Ableitung an der Stelle

auf jeden fall negativ ist, handelt es sich um Hochpunkte.
 Gleichung der Ortskurve der lokalen Extrempunkte aufstellen
Gleichung der Ortskurve der lokalen Extrempunkte aufstellen
Du weißt bereits, dass sich die lokalen Extrempunkte an den Stellen

befinden. Forme diese Gleichung nach

um. Anschließend kannst du dieses Ergebnis in die

-Koordinate der Extrempunkte einsetzen.
1. Schritt: Gleichung umstellen
![\(\begin{array}[t]{rll}
x&=& \frac{1}{2}b &\quad \scriptsize \mid\; \cdot 2 \\[5pt]
2x&=&b
\end{array}\)](https://mathjax.schullv.de/9939385158ceb0bf3d2d0e4a8b9824eb7d06a1736b21cf54e612ef6b362924f3?color=5a5a5a) 2. Schritt:
2. Schritt:  in die Funktionsgleichung einsetzen
in die Funktionsgleichung einsetzen
Berechne zunächst die

-Koordinaten der Extrempunkte:
![\(\begin{array}[t]{rll}
y_b&=& \frac{27}{16}b^4 &\quad \scriptsize \mid\; b=2x \\[5pt]
y_b&=& \frac{27}{16}(2x)^4 \\[5pt]
&=& 27x^4
\end{array}\)](https://mathjax.schullv.de/2f916cd51e7736bd932d233ea087da75518f7db05e1e1867a86337bab201c6db?color=5a5a5a)
Die Ortskurve der lokalen Extrempunkte hat die Gleichung

.
 Koordinaten der Wendepunkte der Graphen
Koordinaten der Wendepunkte der Graphen  berechnen
berechnen
Der Graph der Funktion

hat an der Stelle

einen Wendepunkt, wenn gilt:

und

Berechne dazu als erstes die Nullstellen der zweiten Ableitung der Funktion

und überprüfe anschließend mit der dritten Ableitung, ob es sich um Wendepunkte handelt. In der vorherigen Aufgabe hast du schon berechnet, dass

ist. An dieser Stelle könnte somit der Graph der Funktion einen Wendepunkt haben.
1. Schritt: Nullstellen der zweiten Ableitung berechnen
An der Stelle

könnte der Graph der Funktion einen Wendepunkt haben.
2. Schritt: Überprüfen, ob ein Wendepunkt vorliegt


Der Graph der Funktion

hat in den Punkt

und

jeweils einen Wendepunkt.
 Graphen
Graphen  skizzieren
skizzieren
Die Funktionsgleichung für

lautet:

Zeichne die in den Aufgaben bestimmten Punkte in die Skizze des Graphen

ein.
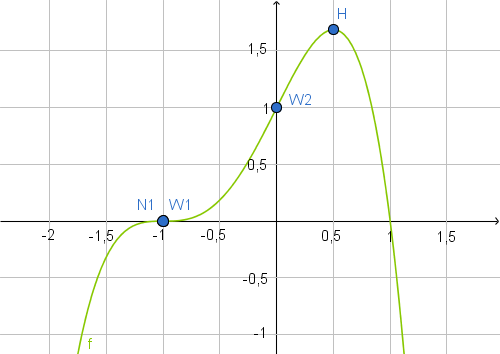 Abb. 1: Skizze des Graphen
Abb. 1: Skizze des Graphen 
 Flächeninhalt in Abhängigkeit von b berechnen
Flächeninhalt in Abhängigkeit von b berechnen
In dieser Aufgabe sollst du den Inhalt der Fläche berechnen, die durch den Graph

und die

-Achse begrenzt wird. Die Grenzen des Intervalls sind somit die Nullstellen des Graphen

. Bilde dazu als erstes eine Stammfunktion der Funktion

und berechne anschließend den Flächeninhalt.
Beide Nullstellen hast du bereits berechnet:

und

.
1. Schritt: Stammfunktion bestimmen
![\(\begin{array}[t]{rll}
f_b(x)&=& (b^2-x^2)\cdot(b+x)^2 \\[5pt]
&=& (b^2-x^2)\cdot(b^2+2bx +x^2) \\[5pt]
&=& -x^4-2x^3b+2xb^3+b^4 \\[5pt]
\end{array}\)](https://mathjax.schullv.de/7a2849e8b6cbbb75fb25a649e0c3c42a1cc6eaa246414bc30a0558580608f903?color=5a5a5a) 2. Schritt: Flächeninhalt berechnen
2. Schritt: Flächeninhalt berechnen
Die Kurve

und die

-Achse schließen eine Fläche mit dem Flächeninhalt
![\(\frac{8}{5}b\,\text{[FE]}\)](https://mathjax.schullv.de/a50de791cf330cd1aab2e5e45982a92627e8e286161ff443e1faa5f19bf7643d?color=5a5a5a)
ein.
 Zielfunktion bestimmen
Zielfunktion bestimmen
In dieser Aufgabe ist die Querschnittsfläche eines Trapezes gegeben und diese soll maximal werden. Stelle also eine Funktion für den Flächeninhalt des Trapezes in Abhängigkeit von

und

auf. Die Formel für den Flächeninhalt eines Trapezes lautet:
In dieser Aufgabe sind:


Wenn du

und

jetzt in die Gleichung einsetzt erhältst du:

Um

in Abhängigkeit von

und

darzustellen, kannst du den Satz des Pythagoras anwenden. Löse die Gleichung nach

auf und setze sie in die Formel für den Flächeninhalt ein.
![\(\begin{array}[t]{rll}
b^2&=&h^2+x^2 &\quad \scriptsize \mid\; -b^2 \mid\;-h^2 \\[5pt]
-h^2&=&x^2-b^2 &\quad \scriptsize \mid\; \cdot (-1) \mid\;\sqrt\; \\[5pt]
h&=&\sqrt{b^2-x^2}
\end{array}\)](https://mathjax.schullv.de/07de9c3d9d8ec877ef94f0e60957715c7a06543c1d2b9444fd3418aa474d164d?color=5a5a5a)
![\(\begin{array}[t]{rll}
A_b(x)&=&(b+x)\sqrt{b^2-x^2}
\end{array}\)](https://mathjax.schullv.de/bc687c6f19326b9f92779af5d9465158309dff51b154384410046b8b9519597c?color=5a5a5a)
Somit hast du gezeigt, dass

die Zielfunktion des Extremwertproblems ist.
 Definitionsbereich der Zielfunktion bestimmen
Definitionsbereich der Zielfunktion bestimmen
Da unter einem Wurzelzeichen keine negativen Zahlen stehen dürfen, muss

sein. Da x und b quadriert werden folgt daraus, dass

sein muss.
Der Definitionsbereich ist somit

 Höhe der Rinne ermitteln
Höhe der Rinne ermitteln
In einer vorherigen Aufgabe hast du berechnet, dass die Höhe

ist. Um nun die maximale Höhe auszurechnen, setzt du für

in die Gleichung ein, denn aus der Aufgabenstellung weißt du, dass der Graph der Funktion

an dieser Stelle ein Maximum hat.
![\(\begin{array}[t]{rll}
h&=&\sqrt{b^2-(\frac{1}{2}b)^2} \\[5pt]
&=&\sqrt{b^2-\frac{1}{4}b^2} \\[5pt]
&=&\sqrt{\frac{3}{4}b^2} = \frac{\sqrt{3}}{2}b
\end{array}\)](https://mathjax.schullv.de/44de1c9d6d26d14c51bca23326201cf326c25a58597b07e157e042b52f8416e7?color=5a5a5a)
Die Höhe der maximalen Querschnittsfläche in Abhängigkeit von b ist

 Aussage beurteilen
Aussage beurteilen
In dieser Aufgabe sollst du die Aussage beurteilen, dass jede lokale Extremstelle der Funktion

auch lokale Extremstelle der Funktion

ist, wobei gilt
![\(z(x)=[g(x)]^2\)](https://mathjax.schullv.de/52d54c528ee11fc26bb91fd3801e4258d1de51579aace242d07fb92cc5912da7?color=5a5a5a)
.
Diese Aussage kannst du widerlegen, indem du eine Funktion

findest, für die die Aussage nicht zutrifft.
Eine mögliche Funktion ist

. Die Funktionsgleichung von

lautet dann:

.
Jetzt kannst du die beiden Funktionen ableiten und berechnen, ob die Ableitungen die gleichen Nullstellen haben.


Das Schaubild der Ableitung

hat nur eine Nullstelle, nämlich bei

. Das Schaubild der Ableitung

hat aber mindestens zwei Nullstellen, welche du direkt ablesen kannst. Die erste befindet sich an der Stelle

und die zweite an der Stelle

.
Somit hat die Funktion

mindestens eine Extremstelle mehr als die Funktion

und du hast gezeigt, dass die Aussage nicht gilt.
 mit
mit  ,
,
 .
.
 .
.
 und untersuche das Verhalten der Funktionen
und untersuche das Verhalten der Funktionen  für
für  .
Jeder der Graphen
.
Jeder der Graphen  besitzt genau einen lokalen Extrempunkt und genau zwei Wendepunkte.
Weise nach, dass die Punkte
besitzt genau einen lokalen Extrempunkt und genau zwei Wendepunkte.
Weise nach, dass die Punkte  diese lokalen Extrempunkte sind und bestimme die Art des Extremums.
diese lokalen Extrempunkte sind und bestimme die Art des Extremums.
 .
Zeichne den Graphen
.
Zeichne den Graphen  im Intervall
im Intervall  .
Die Graphen
.
Die Graphen  schließen jeweils mit der x-Achse eine Fläche vollständig ein. Ermittle mithilfe des Hauptsatzes der Differential- und Integralrechnung die Maßzahl des Inhalts dieser Fläche in Abhängigkeit von Parameter b.
schließen jeweils mit der x-Achse eine Fläche vollständig ein. Ermittle mithilfe des Hauptsatzes der Differential- und Integralrechnung die Maßzahl des Inhalts dieser Fläche in Abhängigkeit von Parameter b.

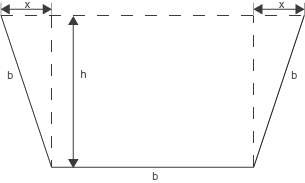 Abb. 1: nicht maßstäblich
Zeige, dass
Abb. 1: nicht maßstäblich
Zeige, dass 
 Gleichung einer Zielfunktion dieser Extremwertproblematik ist und gib einen zugehörigen Definitionsbereich für diese Funktion an.
Jede der Funktionen
Gleichung einer Zielfunktion dieser Extremwertproblematik ist und gib einen zugehörigen Definitionsbereich für diese Funktion an.
Jede der Funktionen  besitzt genau eine lokale Extremstelle und zwar die Maximumstelle
besitzt genau eine lokale Extremstelle und zwar die Maximumstelle  .
Ermittle die Höhe h der Rinne mit maximaler Querschnittsfläche in Abhängigkeit von b.
.
Ermittle die Höhe h der Rinne mit maximaler Querschnittsfläche in Abhängigkeit von b.
 Abb. 1: nicht maßstäblich
Abb. 1: nicht maßstäblich
![\(z(x)=[g(x)]^2\)](https://mathjax.schullv.de/52d54c528ee11fc26bb91fd3801e4258d1de51579aace242d07fb92cc5912da7?color=5a5a5a) definiert.
Beurteile die folgende Aussage:
definiert.
Beurteile die folgende Aussage:
, handelt es sich um eine Minimalstelle.
, handelt es sich um eine Maximalstelle.
und
.
setzt und nach
löst.
einsetzt. So bestimmst du gleichzeitig die Art der Extrema.
